基于寄生行为的双种群萤火虫算法及其在柴油调合中的应用

孔祥东, 钱 锋(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)

基于寄生行为的双种群萤火虫算法及其在柴油调合中的应用

孔祥东, 钱 锋
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)

在实际的化工过程中会遇到许多非线性优化问题。常规群智能优化算法在解决这类问题时,常出现收敛精度差和容易陷入局部最优,本文针对此提出了一种基于寄生行为的双种群萤火虫算法(FAPB)。该算法将进化种群均分为两个种群,通过生物的寄生行为将两个种群联系起来,共享进化信息,提高了全局搜索能力;为防止算法陷入局部最优,引入基于自适应系数的高斯变异机制,提高了局部搜索能力。对4个经典测试函数进行仿真,结果表明:与标准FA算法、FALS算法、LDPSO算法比较,FAPB算法在收敛精度和全局搜索能力上都有较大提升。将该算法应用于柴油调合过程,结果验证了其在实际应用中的可行性。

萤火虫算法; 寄生行为; 局部搜索; 高斯变异; 柴油调合

在现实的工艺流程中会遇到许多非线性优化问题,这类问题的优化结果往往直接关系到工厂的经济效益,所以逐渐成为一个重要的研究方向。针对这类非线性优化问题,常规的解决方法是采用群智能搜索算法,引入各种策略,通过不断地迭代最终找到最优解。常规的群智能算法在寻找最优解的过程中,很容易陷入局部最优,导致搜索效果不理想。后来,部分学者开始尝试将不同的算法进行结合,通过不同算法的优缺点互补来提高算法的整体性能。

受自然界中萤火虫发光特性和群体搜索特性的影响,剑桥学者Yang[1]提出了萤火虫算法 (Firefly Algorithm,FA)。Shruti等[2]将全局最优因子引入到FA模型中,提高了模型的全局搜索能力和搜索精度。Farahani等[3]将高斯变异的机制加入到FA模型的搜索公式中,提高了算法的局部搜索能力和范围,但是,算法在搜索的后期搜索速度会减慢。

针对常规FA及其改进算法的缺点,本文引入了基于寄生行为的双种群萤火虫算法(FAPB)来解决非线性优化问题。该算法通过混沌进行初始化,使初始种群更加均匀地分布在解空间;在进化过程中,通过将寄生行为的策略引入到双种群[4]的FA模型中,极大地提高了种群的搜索能力和收敛精度;在算法后期,为了防止算法陷入局部最优解,将高斯变异引入到局部搜索策略中,提高了算法的局部搜索[5]特性。通过4个测试函数证明了算法的有效性。最后,将该算法应用于柴油调合过程,验证了算法的实际可行性。

1 萤火虫算法

萤火虫算法是基于萤火虫的趋光特性和群体移动特性而提出的一种新兴元启发算法[6],该算法的关键因素在于萤火虫的相对亮度和吸引度[7]。亮度低的萤火虫在移动过程中总是向着亮度高的萤火虫移动,而吸引度的大小则决定了移动距离的大小。所有萤火虫根据亮度和吸引度的不同,不断地搜索和移动,最终聚集在亮度最强的萤火虫附近,从而实现寻优。

萤火虫的相对亮度:

(1)

式中:I0为当前萤火虫的亮度,与所在位置的适应度相关;γ为光在传播介质中的衰减度;rij为空间中2只萤火虫的欧氏距离。

萤火虫的吸引度:

(2)

式中β0为r=0处的吸引度。

萤火虫的位置更新公式:

(3)

式中:αt为搜索步长;rand为(0,1)的随机数。

2 寄生行为

生物共生行为的概念最早是由德国科学家德贝里在1879年提出的[8]。“共生”是指两种生物生活相互交织,共同维持生存的一种状态。共生的两种生物会产生对方需要的物质,维持彼此的生命活动。生物的共生行为具体可分为:互利共生、共栖和寄生。互利共生是指两种生物分别从对方获得好处,维持共同生存;共栖是指只有其中的一方会获得好处,并且另一方不受干扰;寄生是指一种生物寄生在另一生物上不断汲取营养才能生存,获益的一方成为寄生生物,被侵害的生物成为宿主生物。

生物的寄生行为是在生物进化的过程中不断演变而来的。寄生生物和宿主生物根据自然法则,相互竞争、不断适应,最终达到了寄生关系。通常认为,寄生生物会不断汲取宿主生物的营养来维持自身的生命活动;而宿主生物在被寄生生物入侵之后,会获得相应的免疫力,当同种寄生物再次入侵时,会有一定的抵抗力,这一抵抗力又称为获得性免疫。寄生生物和宿主生物共同生活,不断进化,可能会使得寄生生物的入侵能力不断“削弱”,甚至最后达到共生效果[9]。

3 改进的萤火虫算法

3.1 基于寄生行为的双种群搜索策略

在标准FA中,每次迭代萤火虫都会向着周围亮度较强的萤火虫移动,缺少与全局范围内萤火虫信息的交流。为了克服标准FA的缺点,本文将进化种群均分为两个种群,并将生物寄生行为引入到迭代过程中,加强了全局范围内的信息交流,提高了算法的收敛精度和全局搜索能力[10]。

首先对种群进行初始化,并将种群均分为寄生种群Pop1和宿主种群Pop2。在每代的进化过程中会发生寄生行为,具体表现为:对Pop1和Pop2中的粒子按照适应度重新进行排序,将排序后的前50%粒子赋值给寄生种群Pop1,后50%粒子赋值给宿主种群Pop2,完成寄生行为[11]。

寄生行为结束后,寄生种群会继续按照式(3)进行进化。宿主种群由于被寄生种群入侵后产生了获得性免疫,所以在进化时会同时受到邻域粒子和寄生种群粒子的共同影响,按照式(4)进行进化。

(4)

每一代进化结束后,会在Pop1和Pop2中选出全局最优值gbest,并与上一代全局最优位置进行比较,如果比上一代的全局最优位置优越,则替代;否则不做改变。

3.2 基于自适应系数的局部搜索策略

针对进化算法容易陷入局部最优的缺点,本文结合gbest信息,提出了基于自适应系数的局部搜索策略。

首先,通过式(5)对gbest进行局部搜索,得到一组全局最优信息的邻域值。

(5)

式中:ε为自适应系数,其值由式(6)决定。

(6)

式中:MaxIt为最大迭代次数;t为当前迭代次数。

将新得到的gbest的邻域值与gbest进行逐个比较,选出适应度更优的作为新的gbest。

3.3 改进算法步骤

综上所述,FAPB算法步骤如下:

(1) 初始化萤火虫位置,将其均分为Pop1和Pop2,并确定相关参数。

(2) 计算Pop1和Pop2的适应度并排序,更新全局最优值gbest。

(3) 计算萤火虫种群的相对亮度I和吸引度β。

(4) 通过寄生行为,对寄生种群和宿主种群分别采用式(3)和式(4)进行位置更新。

(5) 执行步骤(2),对gbest进行局部搜索策略。

(6) 判断是否满足终止条件,若满足则结束;否则转步骤(3)。

4 仿真结果与分析

为了验证FAPB算法的性能,本文选用4个经典测试函数进行仿真,如表1所示,其中D为测试函数维度,Q为搜索空间范围,fmin为测试函数最优值。将FAPB与LDPSO[12]、标准FA[6]、FALS算法(在标准FA算法中引入本文的局部搜索策略)进行测试对比。为增加结果对比性,公共参数取值均相等,其中最大迭代次数tmax=1 000,种群大小NPop=50,测试函数维度D=30,迭代公式的β0=γ=1。表2示出了对4个测试函数进行30次独立实验的结果。

为了更加直观地看出本文算法的收敛特性,结合图1和图2,对比FAPB算法和FA算法在各个进化阶段的种群收敛情况。从图中可以看出,FAPB算法收敛速度更快,在100代时已经进入了精确搜索的范围,到500代时已经找到了较精确的解;而FA算法直到200代才找到较精确的搜索范围,到500代时也没有找到较精确的解,收敛速度较慢。

图3～图6示出了进化代数与测试函数最优值之间的关系。

表1 基准测试函数

表2 测试结果

图1 FAPB算法的种群收敛情况

由图3～图6可知,标准FA和LDPSO算法的搜索速度较慢,在算法后期容易陷入局部最优。FALS算法由于引入局部搜索策略,虽然有一定跳出局部最优的能力,但是全局寻优能力仍然较差,收敛精度低。而FAPB算法在FALS的基础上,又引入了基于寄生行为的双种群搜索策略,保证了全局范围内粒子信息的交流,提高了算法的全局寻优能力,收敛精度也得到了较大提高。表2结合4个测试函数,从最小值、最大值及平均值3个方面,证明了FAPB在搜索精度和全局收敛性上的优越性。

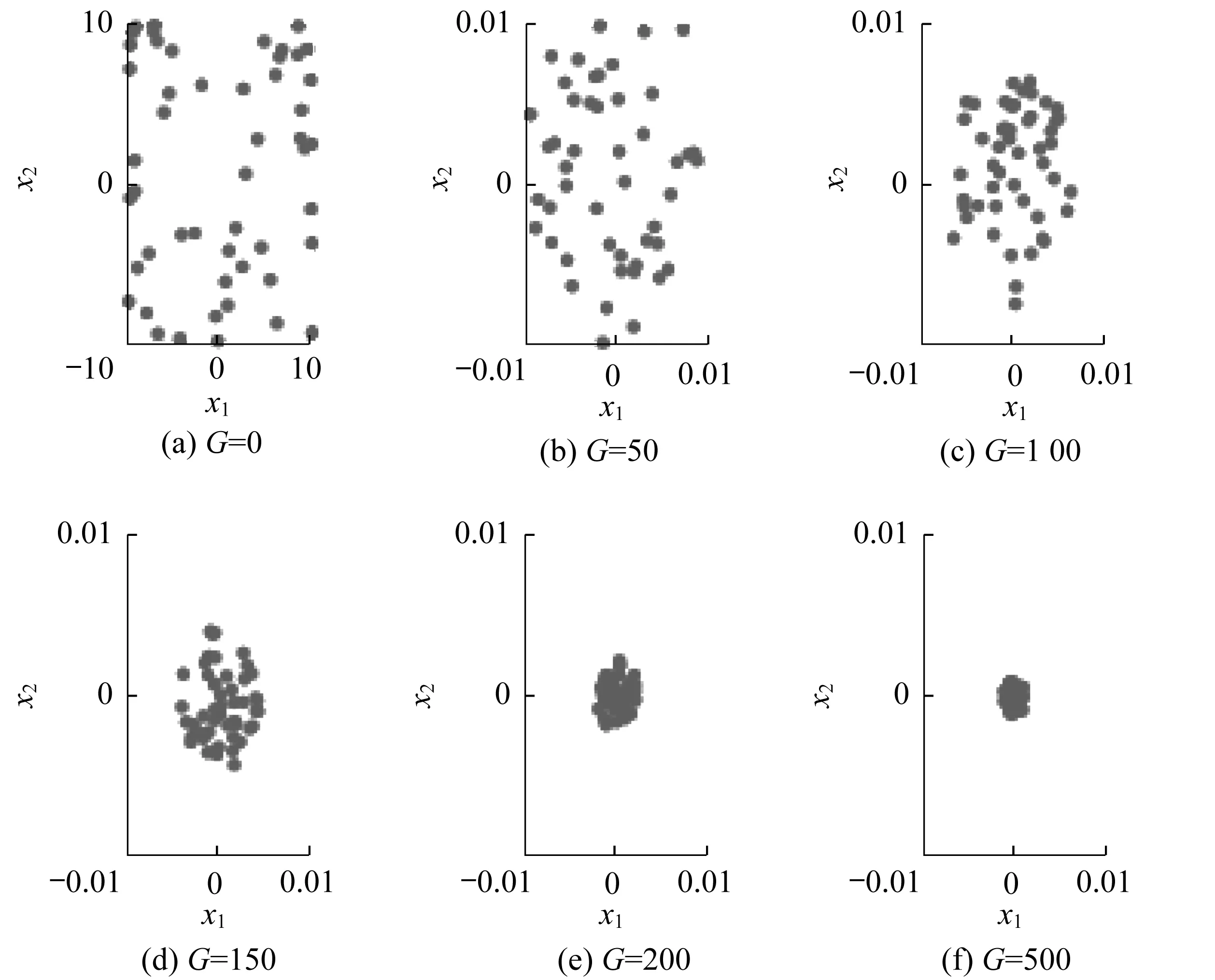
图2 FA算法的种群收敛情况

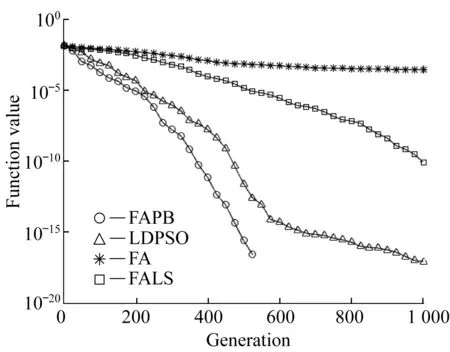
图3 Schaffer函数进化曲线

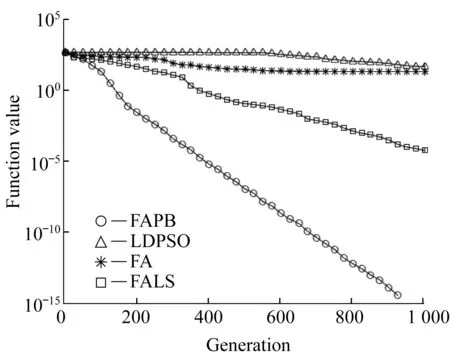
图4 Rastrigin函数进化曲线

图5 Ackleys函数进化曲线

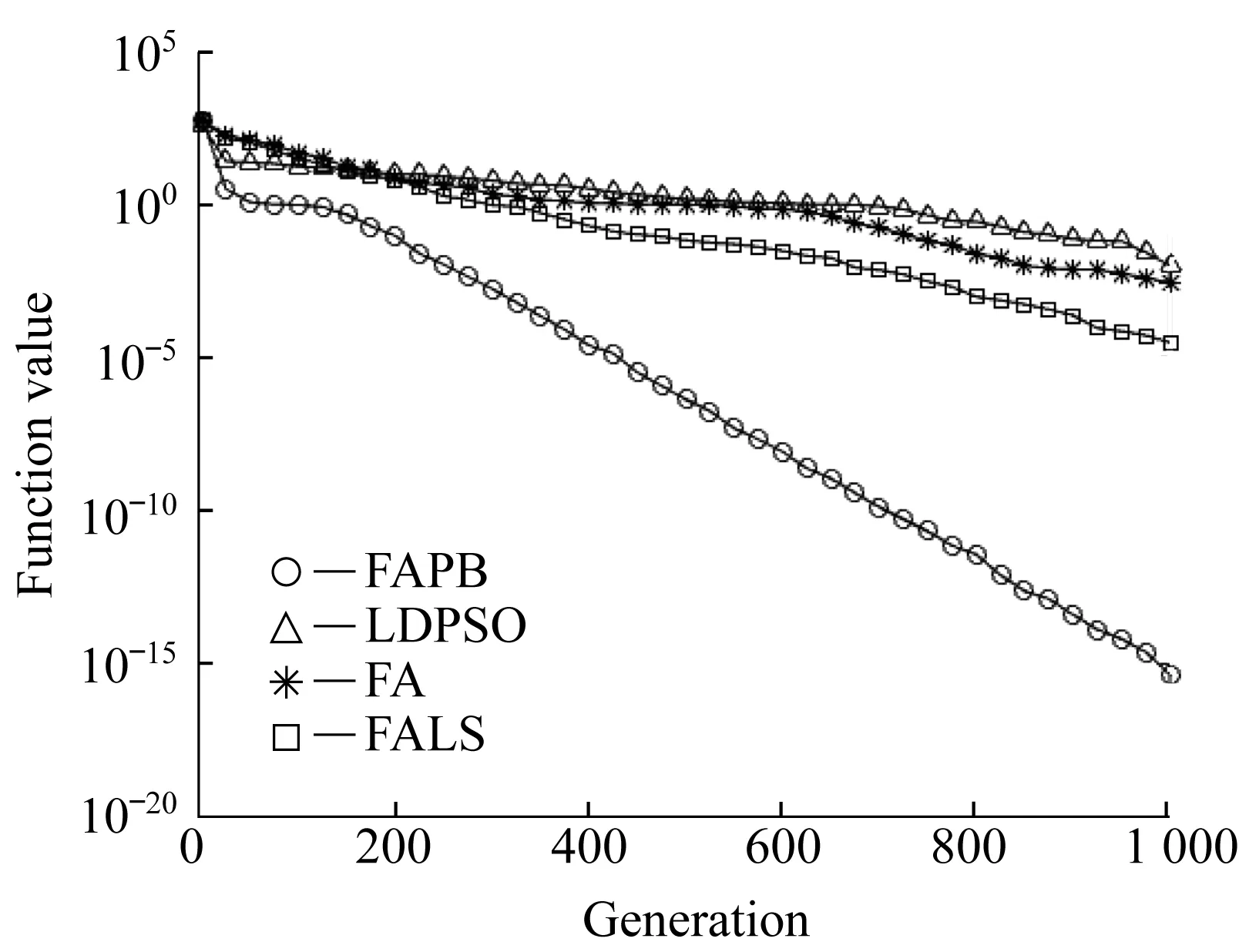
图6 Griwank函数进化曲线

5 应用研究

5.1 问题描述

本文以某炼油厂柴油调合[13]为背景,7种组分油为:I加氢裂化、渣蜡加氢、II柴油加氢、III柴油加氢、IV柴油加氢、II加氢裂化和烷返油。

(1) 目标函数。本文目标函数为各个指标成本最低和质量过剩最小,目标函数模型[14]如下:

(7)

(2) 约束条件。

物料平衡约束:

(8)

库存约束:

(9)

流量约束:

(10)

指标约束:

(11)

(12)

由于调合效应[15]的存在,常规调合模型中线性计算方法已经不能满足实际需求。因此,本文引入指标补偿机制,在计算成品油的各个属性时,对各个属性进行补偿:

(13)

式中:Pzi为每代进化完成后各个组分油的属性值;ΔPbi为各个组分油的属性补偿,通过对每代组分油属性值进行线性回归可得其具体值。

5.2 数据及结果分析

结合表3中的数据,分别对LDPSO[12]、FA[6]和FAPB算法进行了10次实验,其中种群的大小为100,ω1和ω2都为0.5,结果如图7所示。

表3 各个组分油的属性

从图7可以看出,FAPB算法在全局搜索能力和收敛精度两个方面均得到了较大提升。在全局搜索能力方面,LDPSO算法在120代以后趋于稳定,FA算法在150代左右趋于稳定,而FAPB算法由于寄生行为和双种群策略的引入,全局搜索能力得到了提高,在50代左右已经找到了全局最优值;在收敛精度方面,LDPSO算法没有解决容易陷入局部最优的问题,找到的最优值约为4 263.25,FA算法也是受局部搜索能力的影响,找到的最优值约为4 182.49,而FAPB算法引入局部搜索策略,提高了局部搜索能力,最终得到的目标函数值约为4 002.81,优化配方为[0.033 2,0.238 3,0.083 3,0.250 1,0.127 1,0.207 5,0.060 5]。通过对比,可以看出FAPB算法在实际应用中的可行性。

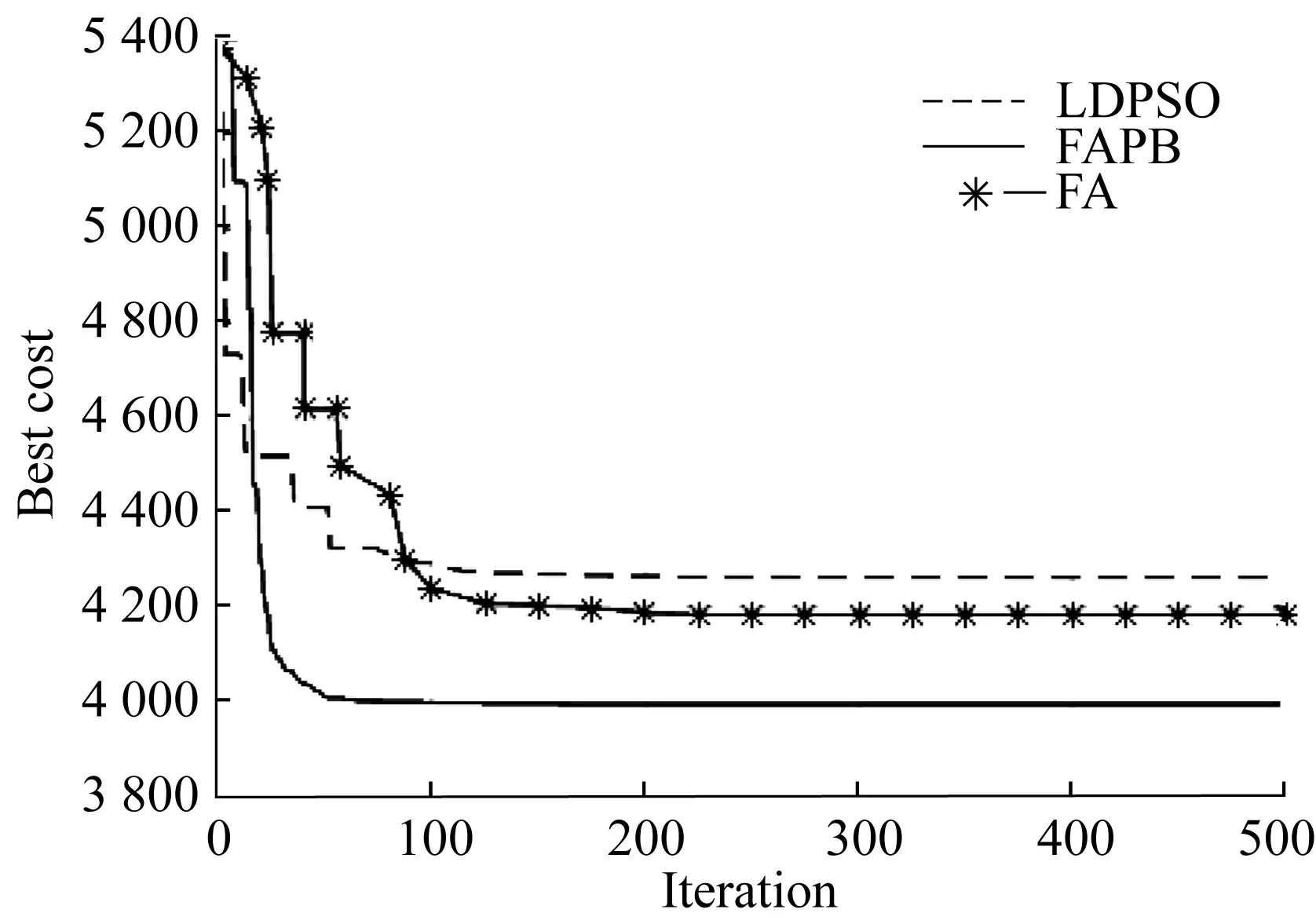
图7 目标函数进化曲线

6 结 论

本文在萤火虫算法(FA)的基础之上,提出了一种基于寄生行为的双种群萤火虫算法(FAPB)。该算法将初始种群均分为两个种群,并将寄生行为加入到进化过程中,提高了种群的全局搜索能力和搜索精度;基于自适应系数的局部搜索策略,提高了种群的局部搜索能力(寄生行为、双种群策略和局部搜索策略的引入,在提高搜索能力和收敛精度的同时,也带来了相应的计算量,算法的运行时间在一定程度上也会相应延长)。通过对4个测试函数的仿真,证明了该算法具有较好的收敛能力和收敛精度。最后,通过柴油调合模型也验证了该算法的可行性。

[1]YANG Xinshe.Nature-Inspires Metaheuristic Algorithms [M].[s.l.]:Luniver Press,2008:83-96.

[2]GOEL S,PANCHAL V K.Performance evaluation of a newmodified firefly algorithm[C]//International Conference on Reliability,INFOCOM Technologies and Optimization.USA:IEEE,2014:1-6.

[3]FARAHANI S M,NASIRI B,ABSHOURI A A,etal.An improved firefly algorithm with directed movement[C]//IEEE International Conference on Computer Science & Information Technology. USA:IEEE,2011:248-251.

[4]李婷,赖旭芝,吴敏.基于双种群粒子群优化新算法的最优潮流求解[J].中南大学学报(自然科学版),2007,38(1):133-137.

[5]刘三阳,张平,朱明敏.基于局部搜索的人工蜂群算法[J].控制与决策,2014(1):123-128.

[6]YANNG Xinshe.Firefly algorithms for mult-imodal optimization[C]//Proceedings of the 5th International Symposium on Stochastic Algorithms:Foundations and Applications.Berlin:Heidelberg Springer-Verlag 2009:169-178.

[7]YANG Xinshe,DEB S.Eagle strategy using lévy walk and firefly algorithms for stochastic optimization[J].Studies in Computational Intelligence,2010,284:101-111.

[8]MCNALLY S F.Symbiosis:Anintroduction to biological associations[J].Bryologist,1988,89(4):88-94.

[9]LI W X,WANG G T.Regulation of parasites on host population:A brief review[J].Acta Hydrobiologica Sinica,2002(5):550-554.

[10]HASSANZADEH T,MEYBODI M R.A new hybrid approach for data clustering using firefly algorithm and K-means[C]// CSI International Symposium on Artificial Intelligence and Signal Processing.USA:IEEE,2012:007-011.

[11]谷金蔚,顾满占,顾幸生.量子寄生遗传算法求解Flow Shop及两阶段配送的集成调度问题[J].华东理工大学学报(自然科学版),2014,40(2):235-243.

[12]SHI Y,Eberhart R C.Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation.USA:IEEE,1999:168-175.

[13]ZHANG B,HUA B,CHEN Q.Optimization of gasoline blending and scheduling in refinery complexes[J].Journal of Chemical Industry & Engineering,2007,58(1):168-175.

[14]崔巍,贾舒晨,周雪山,等.柴油在线优化调和系统在广西石化的应用[J].计算机与应用化学,2013(11):1347-1350.

[15]ZHAO J,CHAI T,PING Z.Modified bio-inspired algorithm based on membrane computing and application in gasoline blending[J].Ciesc Journal,2012,63(9):2965-2971.

A Double Population Firefly Algorithm Based on Parasitic Behavior and Its Application in Diesel Blending

KONG Xiang-dong, QIAN Feng

(Key Laboratory of Advanced Control and Optimization for Chemical Process,Ministry of Education, East China University of Science and Technology,Shanghai 200237,China)

There exist many nonlinear optimization problems in the actual chemical process,for which the conventional swarm intelligence optimization algorithm easily falls into local optimum.This paper presents a parasitic behavior (FAPB) based double population firefly algorithm.By dividing into the evolutionary population into two ones linked together via the parasitic behavior of organisms,these population can share the information and improve the global searching ability.In order to prevent the algorithm from falling into local optimum,this paper further introduces Gauss mutation mechanism based on the adaptive coefficient to improve the local search ability.By simulations on four classical test functions,it is shown that,compared with the standard FA algorithm,FALS algorithm and LDPSO algorithm,the proposed FAPB algorithm can effectively improve the convergence accuracy and global search capability.Finally,the feasibility of the proposed algorithm is also demonstrated via diesel blending.

firefly algorithm; parasitic behavior; local search; Gauss variation; diesel blending

1006-3080(2017)02-0213-07

10.14135/j.cnki.1006-3080.2017.02.010

2016-09-09

国家自然科学基金重点项目(61333010);国家自然科学基金面上项目(21376077,61403141);上海市“科技创新行动计划”研发平台建设项目(13DZ2295300)

孔祥东(1990-),男,硕士生,研究方向为化工过程优化。E-mail:425589306@qq.com

钱 锋,E-mail:fqian@ecust.edu.cn

TE624

A