利用MATLAB生成Koch曲线
2017-04-27张笑笑
张笑笑
摘 要 分析Koch曲线的构造过程,然后编写生成Koch曲线生成元的M函数,通过该M函数的递归调用来生成Koch曲线。通过Koch曲线,便于更直观地理解分形,获得分形带来的艺术美感。
【关键词】分形 Koch曲线 递归
自然界存在许多复杂事物和现象,如蜿蜒曲折的海岸线、天空中奇形怪状的云朵、错综生长的灌木、太空中星罗棋布的星球等,还有许多社会现象,如人口的分布、物价的波动等,它们呈现异常复杂而毫无规则的形态,但它们具有自相似性。人们把这些部分与整体以某种方式相似的形体称为分形(fractal),在此基础上,形成了研究分形性质及其应用的科学,称为分形理论。Koch曲线由瑞典数学家科赫(Koch)于1904年提出,是典型的分形曲线。
MATLAB(MATrix LABoratory)是颇具特色和影响的科学计算软件,它以矩阵运算为基础,将高性能的数值计算和符号计算功能、强大的绘图功能、动态系统仿真功能以及为数众多的应用工具箱集成在一起,在科学研究以及工程设计领域有着十分广泛的应用。本文以Koch曲线为例,利用MATLAB作为实现工具,说明分形曲线的生成方法。
1 Koch曲线的构造过程
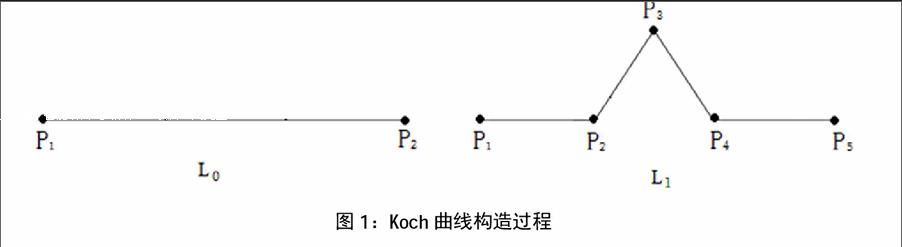
Koch曲线的构造过程是,取一条直线段L0,将其三等分,保留两端的线段,将中间的一段用以该线段为边的等边三角形的另外两边代替,得到曲线L1,如图1所示。再对L1中的4条线段都按上述方式修改,得到曲线L2,如此继续下去进行n次修改得到曲线Ln,当n→∞时得到一条连续曲线L,这条曲线L就称为Koch曲线。
Koch曲线将每条直线用一条折线替代,这条折线通常称为该Koch曲线的生成元。曲线的特征完全由生成元决定。给定不同的生成元,就可以生成各种不同的分形曲线。分形曲线的构造过程是通过反复用一个生成元来取代每一直线段,因而图形的每一部分都和它本身的形状相同,这就是自相似性,这是分形最为本质的特点。
对于给定的初始直线L0,需要在线段P1P5中插入三个点,其中P2,P4为线段P1P5的三等分点, P3可以由P4以P2为轴心逆时针旋转60°得到。
先考虑坐标数据的处理方法,即根据P1,P5两点的初始坐标,按照Koch曲线的构成原理计算出 P2,P3,P4各点坐标。显然:
P2=P1+(P5-P1)/3
P4=P1+2( P5-P1)/3
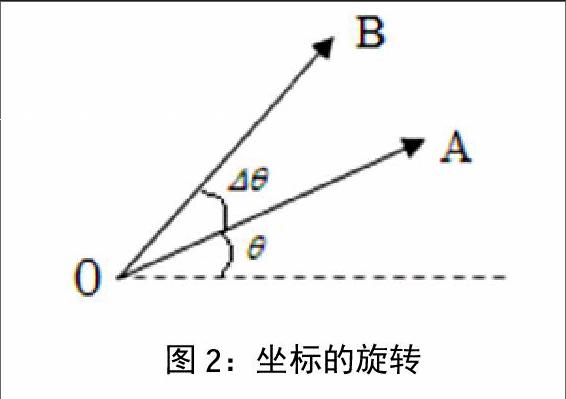
为了得到P3点坐标,引入旋转矩阵。点A对应于长度为r的向量,A逆时针旋转△θrad得到B,如图2所示。
由此,定义旋转矩阵:
则
B=ART
P3点坐标可以由以下旋转矩阵来实现。
R用于对坐标进行60°的旋转,则P3点坐标可以由如下的公式得到:
2 Koch曲线的实现
分形曲线的构造过程也决定了生成该曲线可以用递归方法,即函数自己调用自己的过程。定义对直线L0进行替换的函数koch(),然后利用函数的递归调用,分别对P1P2、P2P3、P3P4、P4P5线段调用koch函数,通过递归来实现替换。程序不能像数学家的设想那样运算至无穷,所以要根据要显示的最小长度作为递归的终止条件。
首先编写M函数koch.m如下:
function y=koch(P1,P5,Level)
if Level<1
plot([P1(1),P5(1)],[P1(2),P5(2)],'k'); %绘制曲线
hold on;
else
R=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)]; %旋转矩阵
P2=P1+(P5-P1)/3; %计算P2,P3,P4各点坐标
P4=P1+2*(P5-P1)/3;
P3=P1+(P5-P1)/3+(P5-P1)*R'/3;
koch(P1,P2,Level-1); %函数递归调用
koch(P2,P3,Level-1);
koch(P3,P4,Level-1);
koch(P4,P5,Level-1);
end
M函數编写完成后,编写以下程序。
koch([0,0],[1,0],5);
axis equal
axis([0,1,-0.05,0.35])
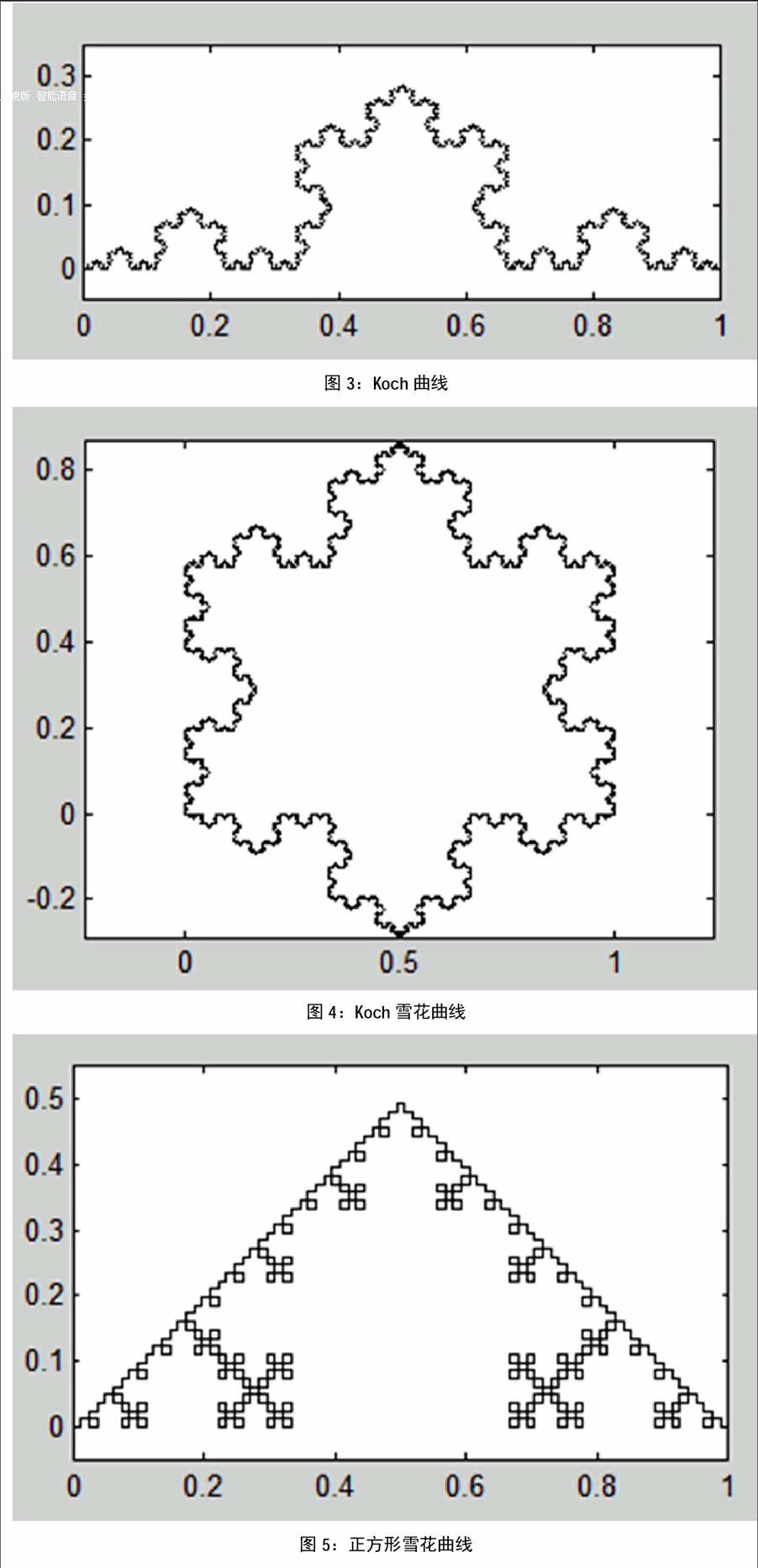
程序取Level=5,P1=[0,0],P5=[1,0],运行结果如图3所示。改变Level的值可以获得不同细腻程度的Koch曲线。
在程序中三次调用koch.m函数,实现三角形三条边各自的Koch曲线,形成Koch雪花曲线效果。编写以下程序,其运行结果如图4所示。
koch([1,0],[0,0],5);
koch([0,0],[cos(pi/3),sin(pi/3)],5);
koch([cos(pi/3),sin(pi/3)],[1,0],5);
axis equal
3 Koch曲线的变形
参照本文的方法,我们很容易自己构造其他生成元的Koch曲线,并利用MATLAB来实现。例如,修改Koch曲线生成的方法,将线段中凸起“三角形”改为凸起“正方形”,从而形成一种正方形雪花曲线,如图5所示。
4 结束语
分形几何是一门以不规则几何形态为研究对象的几何学。由于不规则现象在自然界普遍存在,因此分形几何学又被称为描述大自然的几何学。分形几何学建立以后,很快就引起了各个学科领域的关注,不仅在理论上,而且在实用上分形几何都具有重要价值。通过利用计算机和MATLAB来生成分形曲线的图像,使得我们可以更直观的感受和理解分形,以及分形带来的艺术之美。
参考文献
[1]百度百科.分形理论.http://baike.baidu.com/view/86848.htm.
[2]刘卫国.MATLAB程序设计教程(第二版)[M].北京:中国水利水电出版社,2010.
[3]PRATAP R.Getting Started with MATLAB: A Quick Introduction for Scientists and Engineers.Oxford University Press, New York, 2009.
[4]百度文库.几个分形的matlab实现.http://wenku.baidu.com/view/e34f87240722192e4536f659.html.
作者单位
湖南省长沙市第一中学 湖南省长沙市 410005
