基于键相插值法的叶片振动测量研究*

王维民， 任三群， 陈立芳， 邵化金

(北京化工大学高端机械装备健康监控与治愈化北京市重点实验室 北京，100029)



基于键相插值法的叶片振动测量研究*

王维民， 任三群， 陈立芳， 邵化金

(北京化工大学高端机械装备健康监控与治愈化北京市重点实验室 北京，100029)

研究了转速波动对叶尖定时测量精度的影响及解决方法，以非接触式叶尖定时测振法为基础，引入键相插值法解决如升(降)速、转速波动等情况下的单键相涡轮机叶片振动测量误差较大的问题，同时对恒速运转下也可自适应测量。首先通过建立仿真模型比较在不同波动频率下键相插值法与单键相法的结果，结果表明在波动周期较大或波动的转速幅值较大等情况下，使用键相插值法计算的结果，其精确度明显提高。最后分别通过模拟叶轮实验台和真实叶轮实验台进行了实验验证。结果表明，笔者所提出的键相插值法可以有效地提高转速波动过程中的叶片振动位移测量，对解决工程实际问题具有较大的参考价值。

叶尖定时； 叶片振动； 转速波动； 单键相； 键相插值

引 言

在叶片振动测量领域，叶尖定时法(blade tip timing,简称BTT)是一种非常重要的非接触式测量手段，相较于应变片法，该方法由于可对整机叶片进行测量，不会带来气流扰动影响等优点而受到众多透平企业和研究人员的重视[1-2]。近年来，叶尖定时法主要用在叶片振动测试[3]、非接触式应力测量[4]，裂纹故障的预警[5]、失谐叶盘的振型分析[6]以及叶盘系统的阻尼评价[7]等领域。

以上应用对叶片振动测量精度有较高的要求，如何精确测量叶片的振动幅值成为关键。叶尖定时测量法基本原理为通过计算旋转叶片经过传感器的理论到达时间和实际到达时间的差值，将该时间差值与对应叶片的线速度相乘并经过相关算法分析进而获得叶片振动幅值、相位、频率等信息[8-9]。设置键相的目的是计算旋转转速，及以键相为参考计算叶尖理论到达时间[10]。然而在实际的测量中，叶尖的理论到达时间受转速波动的影响，而实际达到时间又受到叶片加工误差、轴向位移、径向振动等因素的影响。文献[9]提出了转速波动的影响，但并未就具体的解决方案进行深入的研究。文献[1]研究了叶尖几何形状制造误差多传感器不对中的影响并提供了专利技术，文献[12]提出了不依赖键相传感器的叶片振动测量方法，但该方法对叶片加工的误差信息有较高的要求。

针对在计时过程中以单键相作为参考会导致计算实际到达的时间误差增大的情况，笔者引入键相插值方法来计算实际到达时间，通过理论推导，建模仿真验证该方法的可行性，并通过两个实验台，开展实验研究。研究结果表明，键相插值法可以有效地提高转速波动过程中的叶片振动位移测量，可为后续的叶片振动参数分析提供较好的数据基础。

1 叶片振动位移分析方法

1.1 叶尖计时法简介(单键相法)

使用单键相时的叶尖计时测量原理示意图如图1所示。图中：B1，B2，…分别表示叶片数；tkn，tkn+1为健相时间戳。

(1)

(2)

故

(3)

其中：n为转数；b为叶片编号，1,2,3，…，B；B为叶片数；tKn,tKn+1为键相时间戳；vn为n转时的线速度；R为叶片半径；xDC为恒偏量或称直流分量，可通过低转速标定或理论计算获得；xbn为叶片b在n转时的振动位移。

当运行转数恒定时，即Tn保持不变，上式对各叶片振动位移的计算是准确的。但是，当叶片在旋转的过程中，由于各种原因导致转速不稳定则会导致在计算叶片振动位移时引入较大的计算误差。故此引入键相插值法来降低由于单键相对振动位移计算的误差影响。

1.2 键相插值法理论推导

本方法主要针对单键相测振系统对叶片振动位移计算方法作了改进。在tKn,tKn+1之间通过线性插值的方法虚拟出B-1个参考键相点，由于这些参考键相点在单键相测振系统中是不存在的，称为键相插值点。与第1个参考键相点tKn共同组成本转内B个叶片相对应的参考键相。键相插值的原理示意图见图1，图中分析对比在转速波动情况下的振动位移的表示方法。

键相插值点可由下式确定

(4)

其中：B为叶片总数；tKbn为参考键相，即叶片b在n转时的参考键相。

根据式(3)可得，键相插值法的叶片振动位移为

(5)

化简得

(6)

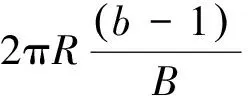
故可得键相插值情况下，叶片振动位移计算公式为

(7)

2 仿真模型建立与结果验证

2.1 仿真模型介绍

为了通过仿真方法验证键相插值法的可行性，需要得到与实际测量过程相类似的一系列时间点来做分析。一般叶片在旋转过程中以近于谐振动形式振动的[13]，振动位移方程可简化为

(8)

其中：A为振动幅值；ω为振动角频率；φ0为初始相位。

仿真中为了简化复杂度，只考虑一阶振动，忽略高阶振动。将高速旋转叶片的振动过程简化为叶片旋转和叶片振动，单位统一用弧度表示，这也简化了叶片振动方程的表述。其中主弧度方程表示叶片的旋转过程(旋转方程)

(9)

(10)

其中：N为仿真点数，与时间有关的量；Ω为在点i时的转速，单位r/min；t为时间，本仿真是按1s为108步长计算。

振动弧度方程表示叶片在旋转过程中的振动，其中，f表示叶片的振动频率。由式(8)得

(11)

由式(9)和式(11)得出，叶片在N时(或t=N/108)的振动累积弧度为

(12)

为了仿真叶片经过传感器时被传感器捕捉到实际到达传感器的时间。仿真中每一转内，使叶片的弧度累积到一定值时的第一个点即为实际到达传感器的时间。为了方便计算，根据旋转可得，检测方程为

(13)

键相传感器的检测方式与上式相同，可减少编程计算的复杂度。

为了与实验相参照，假设叶片个数B=16，取键相与叶片1之间的夹角为0，各叶片等间距分布，叶片振动初始相位为0。仿真的叶片编号为1, 4, 6, 8, 10, 12, 14, 15, 16，其对应的叶片振动频率为1 806 Hz；叶片编号2的振动频率为1 807 Hz[14]。取A/R=0.004。则叶片1, 4, 6, 8, 10, 12, 14, 15, 16的振动累积弧度方程可表示为

(14)

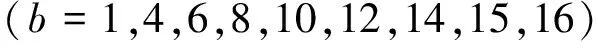
叶片2的振动累积弧度方程为

(15)

转速波动方程为

(16)

其中：An为波动转速的波动幅值；fn为波动转速的波动频率。

2.2 仿真及结果分析

在上述仿真方程的基础上，基于4 800r/min做了以下6种情况的仿真实验(为了简化将初始相位角设为0)。基准误差是仿真实验中叶片经过传感器时的振动位移获得的振动幅值与理论振动幅值之比。

表1 转速波动的幅值和频率

通过以上仿真结果可以得出，键相插值法较单键相法在转速波动过大，且波动频率不大时改善显著。如图2，3所示，当转速波动幅值为5 r/min，频率为11 Hz时基准误差与键相插值法误差相近，而单键相法偏离较大，叶片编号10以后的数据误差较大。同样，当波动幅值增大到10和20 r/min时，键相插值法仍然具有较高的精度，而单键相法误差逐步增大。当波动频率为55 Hz时，在低波动幅值下(5 r/min),键相插值法仍然具有较高的精度，但是当波动幅值增大到10 r/min甚至更高时(20 r/min)，键相插值法的改善效果会有所降低，但单键相法误差更大，此时需要通过其他方法来解决由于转速波动过大而导致的叶片振动测量误差较大的问题。由此可见，在一定程度上引入键相插值会提高叶片振动的测量精度，且不会带来附加影响。

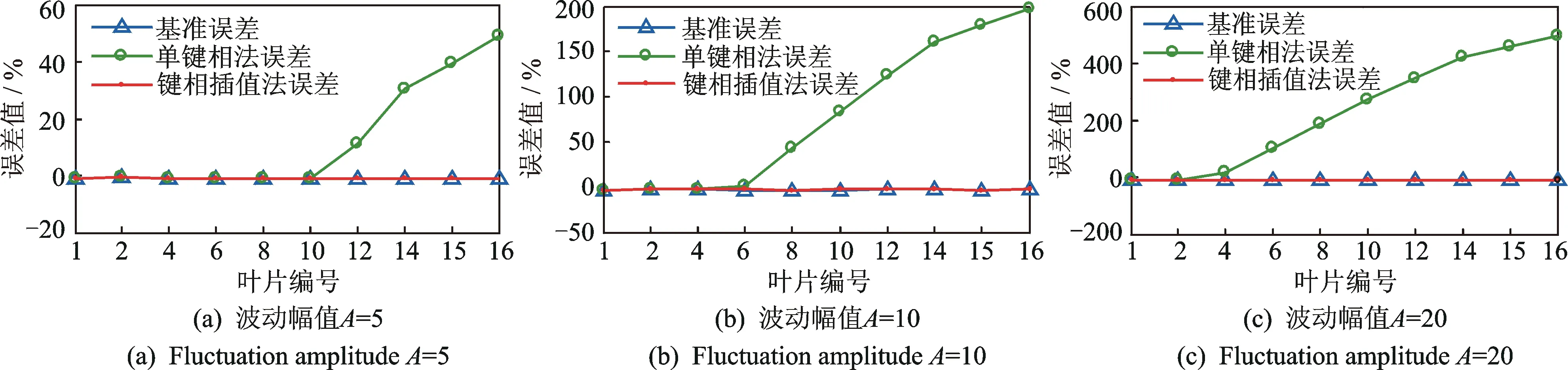
图2 转速波动频率为11 Hz时各波动幅值下的误差对比Fig.2 Comparing vibration amplitude error under different fluctuation amplitude at the speed fluctuation of 11 Hz

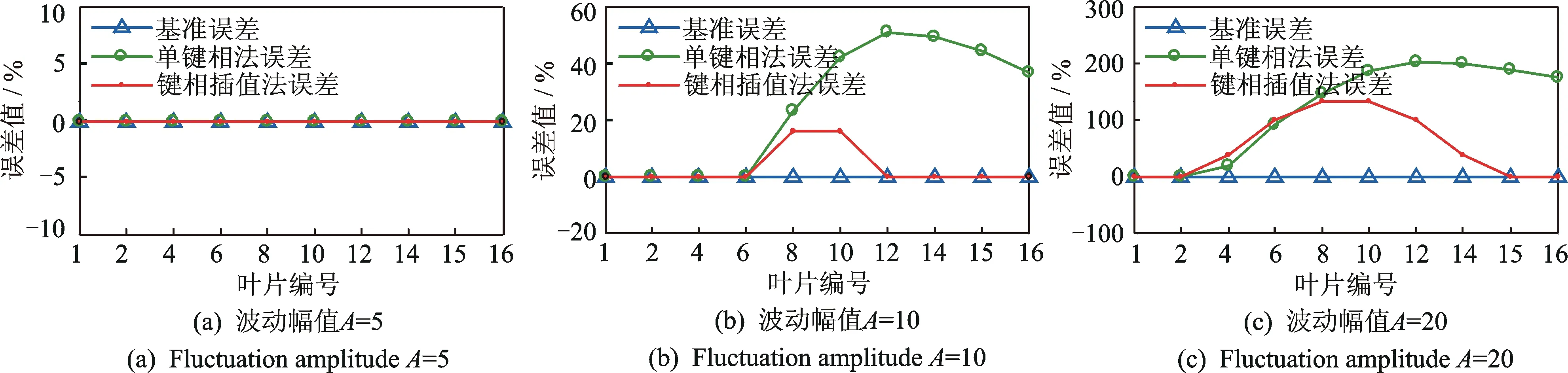
图3 转速波动频率为55 Hz时各波动幅值下的误差对比Fig.3 Comparing vibration amplitude error under different fluctuation amplitude at the speed fluctuation of 55 Hz

2.3 实验台1对键相插值法的验证

实验台由模拟涡轮叶片的柔性直叶片(叶片直径100 mm，叶片个数为16)、cDAQ-9174采集设备(带NI9402采集卡)、一套Bently 3300 XL 8 mm电涡流传感器、两套光纤传感器、光电探测器、激光源、变频器、无刷直流电机、驱动器及其他辅件组成，如图4所示。

图4 直叶片振动监测实验台及叶片Fig.4 Blade vibration monitoring apparatus

在上述实验台的基础上，进行了4 200 r/min和2 400 r/min两种转速的测试。4 200 r/min时，取叶片编号1的振动位移放大图，如图5所示。

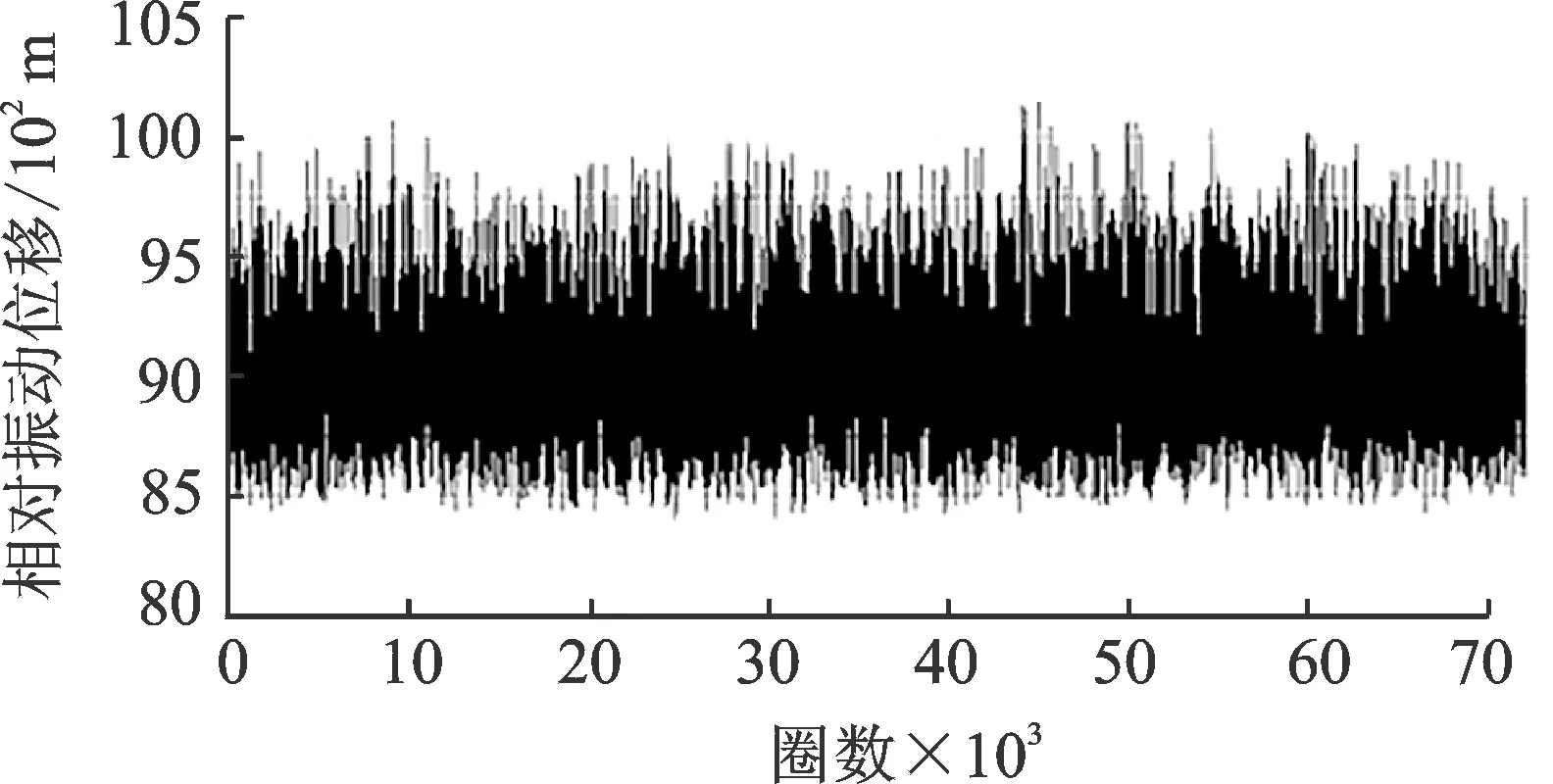
图5 单键相法测得叶片编号1的振动位移Fig.5 Blade No.1 vibration displacement by KPIM

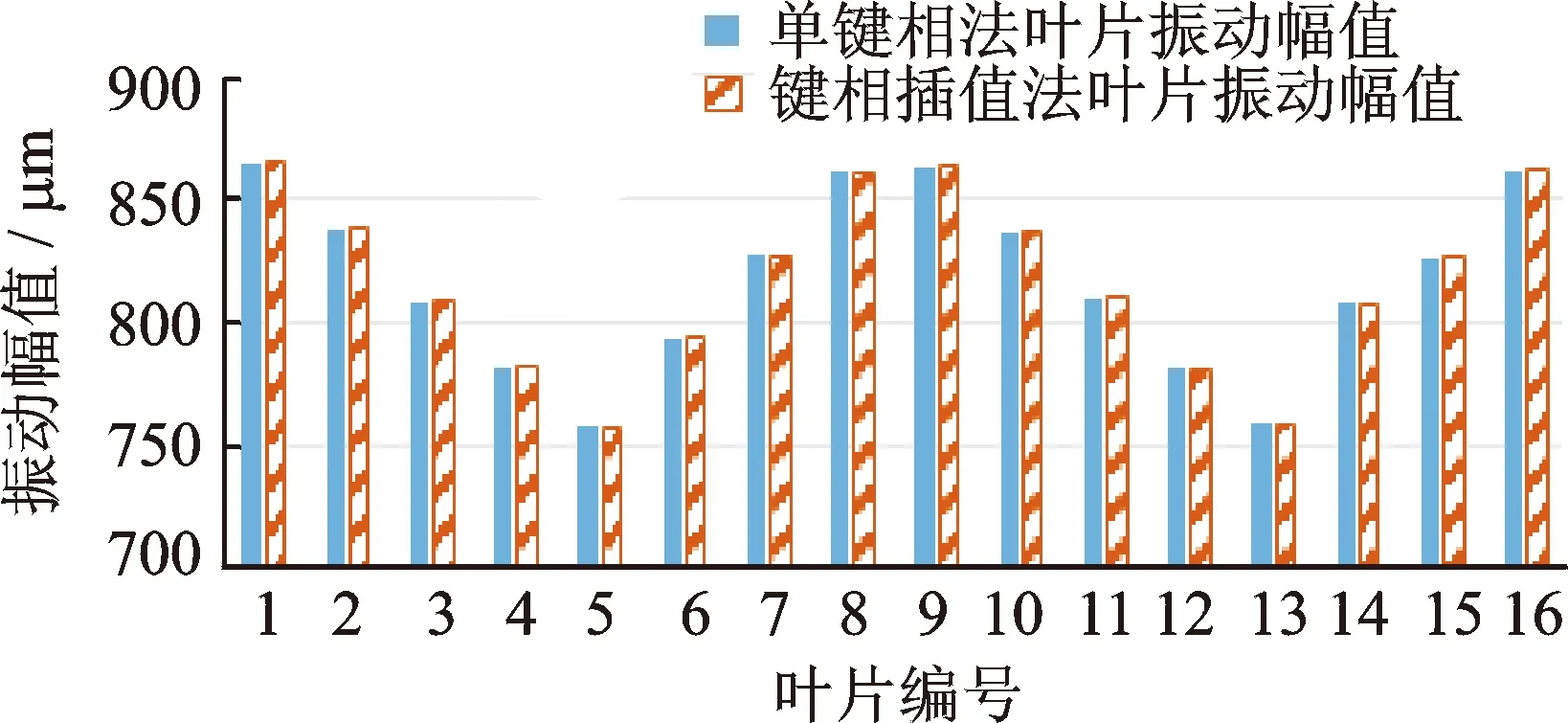
图6 4 200 r/min时单键相法与键相插值法结果对比Fig.6 Comparing the results of single phase method and KPIM at the speed of 4 200 r/min

图6为单键相法和键相插值法求得的叶片振动幅值之间的对比。通过分析转速情况可知，转速波动幅值小于6 r/min，波动频率超过30 Hz(且有噪声干扰)，两种方法测出的叶片振动幅值接近，与上述仿真结论较为接近。运行转速为2 400 r/min时， 两种方法获得的叶片振动幅值大小差别几乎为0，如图7所示。分析转速发现，转速波动幅值小于2 r/min，且波动频率在20～30 Hz(有噪声干扰)。以上两种转速实验与仿真结果得出的结论一致。

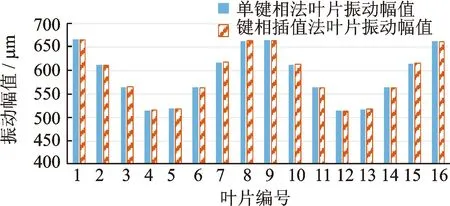
图7 2 400 r/min下单键相法与键相插值法结果对比Fig.7 Comparing the results of single phase method and KPIM at the speed of 2 400 r/min

2.4 实验台2介绍与实验结果

实验台2中采用扭转叶片，如图8所示。叶盘外圆直径137 mm，叶片个数为32，整个涡轮叶片采用铝合金数控铣加工而成。

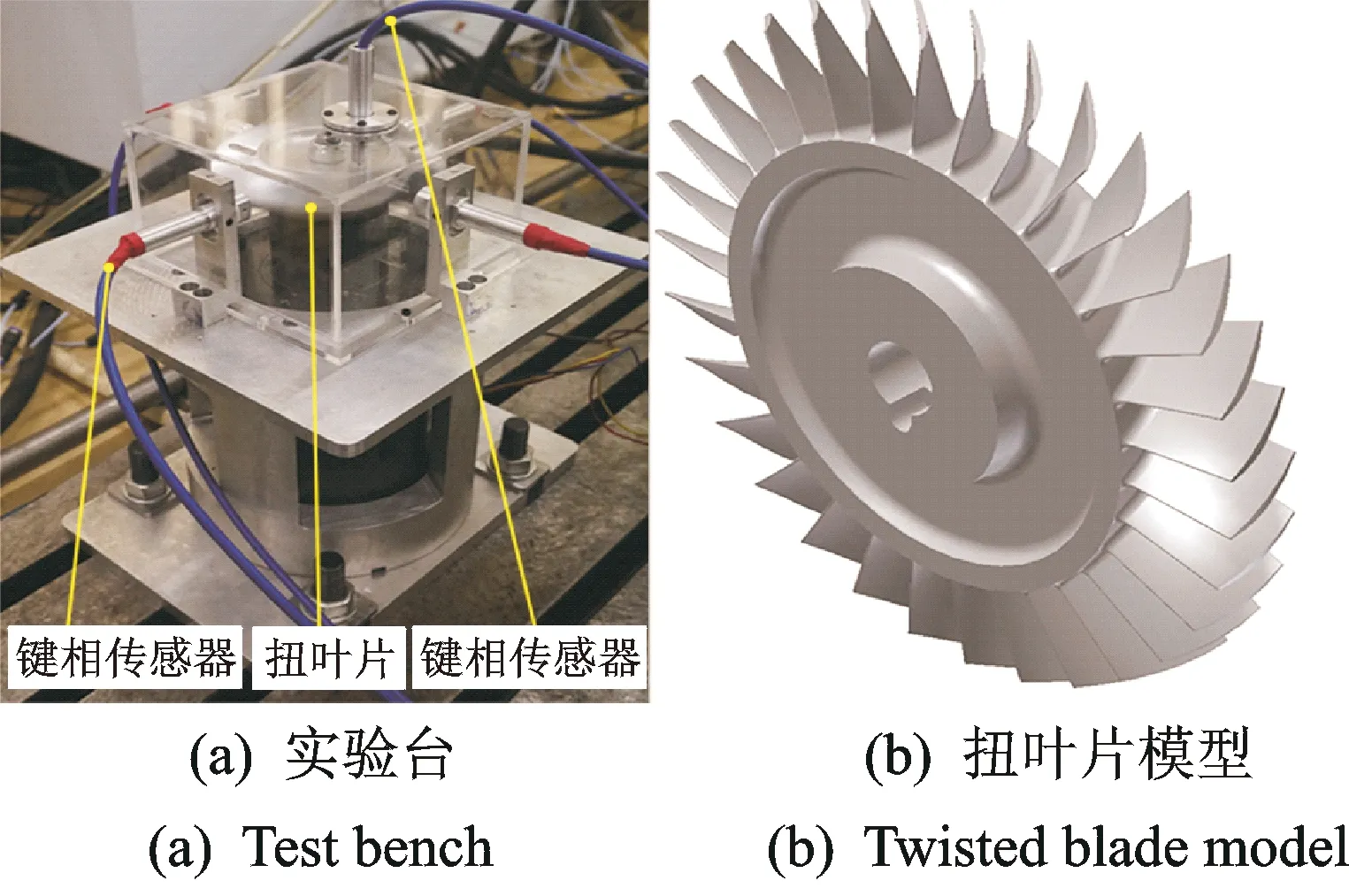
图8 实验台与扭叶片模型Fig.8 The test bench and twisted blade model

在上述实验台的基础上为了探究键相插值法的可行性，进行了4 800 r/min的运转实验。运用单键相法测得叶片编号1的振动位移，如图9所示。

通过图9可以看到两个现象:一是叶片偏向一侧振动位移较大，而另一侧很小；二是随着运转时间的增加，叶片的平衡位置会向上漂移。在对6 000,7 200,8 400,9 600 r/min这4个转速的实验中，也都出现上述两个现象。

现象一的发生是由于扭叶片本身结构原因所导致的。叶片弯曲振动可分为切向振动和轴向振动，分别沿最小主惯性轴和最大主惯性轴振动，扭叶片的最小主惯性轴与轴线不平行，且左右的抗弯截面系数不同会导致叶片出现上述振动现象。对现象二进行了长时间的运转实验与监测，发现在运转超过4 min后该漂移现象趋于平缓，10 min之后平衡位置几乎不变。这种现象发生原因是由于在初始运转的过程中叶片对热膨胀效应较为敏感，导致叶顶发生轴向位移，进而表现为叶顶到达传感器的时间发生改变，随着运转时间的增长，热膨胀效应达到极限，进而平衡位置不再发生改变。

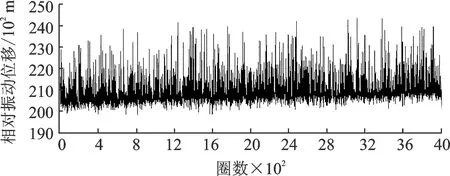
图9 叶片编号1振动位移图Fig.9 Blade No.1 vibration displacement diagram

相较于直叶片，扭叶片振动形式更为复杂，导致键相插值法的使用受到较大限制，但扭叶片应用更为普遍，需要继续研究真实叶片振动及测试方法。

3 结 论

1) 完成了键相插值法的理论推导，并建立了仿真数学模型。进行了不同波动转速下的仿真，仿真的结果表明在对转速波动较大且波动频率不大时会对测量结果带来很大的改善，同时对波动频率较高或恒转速情况下可以自适应。

2) 通过直叶片实验台进行了叶片振动位移测量实验，在运行转速为2 400 r/min和4 200 r/min时，两种方法测得的振动幅值的大小较为接近，通过对转速进行分析可知由于转速波动很小导致，这也验证了仿真的结果。

3) 为了与工程应用中使用的真实叶片更为接近，使用了扭叶片进行相关实验，在监测叶片振动位移的过程中，出现了叶片单侧振动位移较大，另一侧振动位移很小的现象，同时随着运转时间的增加平衡位置有漂动。上述现象的出现，虽然不能为验证键相插值法提供依据，但为进一步解决工程实际问题提供了更多的思考方向。

[1] Kaszynski A A, Brown J M. Accurate blade tip timing limits through geometry mistuning modeling[C]∥ASME Turbo Expo 2015: Turbine Technical Conference and Exposition. Montréal, Canada:American Society of Mechanical Engineers, 2015.

[2] Knappett D, Garcia J. Blade tip timing and strain gauge correlation on compressor blades[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2008, 222(4):497-506.

[3] Gallego-Garrido J, Dimitriadis G, Wright J R. A class of methods for the analysis of blade tip timing data from bladed assemblies undergoing simultaneous resonances—part i: theoretical development[J]. International Journal of Rotating Machinery, 2007, 2007:11.

[4] Pickering T M. Methods for validation of a turbomachinery rotor blade tip timing system[D]. Blacksburg: Virginia Polytechnic Institute and State University, 2014.

[5] Hu Zheng, Lin Jun, Chen Zhongsheng, et al. A non-uniformly under-sampled blade tip-timing signal reconstruction method for blade vibration monitoring[J]. Sensors, 2015, 15(2):2419-2437.

[6] Salhi B, Lardiès J, Berthillier M, et al. Modal parameter identification of mistuned bladed disks using tip timing data[J]. Journal of Sound & Vibration, 2008, 314(3):885-906.

[7] Abdelrhman A M, Hee L M, Leong M S, et al. Condition monitoring of blade in turbomachinery: a review[J]. Advances in Mechanical Engineering, 2014, 2014:10.

[8] 王萍. 叶尖定时方法在国外航空发动机叶片振动测量中的应用综述[J]. 航空科学技术, 2013,6(6):5-9.

Wang Ping. Application review of blade tip timing method for foreign aero-engine blade vibration measurement[J]. Aeronautical Science & Technology, 2013,6(6):5-9. (in Chinese)

[9] Carrington I B. Development of blade tip timing data analysis techniques[D]. Manchester: University of Manchester, 2002.

[10]邓勇, 盛鑫志, 薛秀生. 光纤叶片振幅监测系统应用试验研究[J]. 航空动力学报, 1992,2(2):156-158.

Deng Yong, Sheng Xinzhi, Xue Xiusheng. A fibre-optic amplitude monitor for blade vibration[J]. Journal of Aerospace Power,1992,2(2):156-158. (in Chinese)

[11]Twerdochlib M. Method of matching sensors in a multi-probe turbine blade vibration monitor:US,US7987725[P], 2011-08-02.

[12]Guo Haotian, Duan Fajie, Zhang Jilong. Blade resonance parameter identification based on tip-timing method without the once-per revolution sensor[J]. Mechanical Systems and Signal Processing, 2016, 66(2016): 625-639.

[13]萨勃洛斯基ИE. 涡轮机叶片振动的非接触测量[M].吴士祥,郑叔琛,译.北京:国防工业出版社,1986:40-43.[14]张玉贵. 烟气轮机叶片振动的非接触式在线监测关键技术研究[D]. 天津:天津大学, 2008.

*国家自然科学基金面上资助项目(51275028);国家自然科学基金重点资助项目(51135001);中央高校基本科研业务费专项资金资助项目(JD1508)

2015-04-17；

2015-09-20

10.16450/j.cnki.issn.1004-6801.2017.02.025

V216.2; TH45

王维民，男，1978年4月生，博士、教授、博士生导师。主要研究方向为旋转机械动力学分析、状态监测及故障诊断。曾发表《An identification method for damping ratio in rotor system》(《Mechanical Systems and Signal Processing》2016,Vol.68-69)等论文。 E-mail：wwmbuct@163.com