我国住宅商品房价格影响因素研究——基于空间计量模型

（上海师范大学 商学院，上海 200234）

我国住宅商品房价格影响因素研究
——基于空间计量模型

包舒雨

（上海师范大学 商学院，上海 200234）

住房问题关系到国计民生，一直备受关注，国家政策也大力支持房地产行业的发展，但随着经济的发展、物价上涨等经济环境的变化，高房价问题已成为重大经济问题。本文引用了2005—2014年我国31个省的住宅商品房价格的空间面板数据，运用空间计量模型，分析了人均国内生产总值和工业化水平对房价的影响，并在此基础上分析了我国住房价格的空间溢出效应。另外，也对我国房价进行了区域差异分析。结果显示：人均gdp和工业化水平对于住房价格有正向的促进作用，我国住房价格在空间上具有较强的集聚效应。我国房价从区域上来看，从东部向西部呈现递减的规律。

人均gdp；工业化水平；住房价格；K-means聚类；空间溢出效应

一、引言

自从1979年我国开始全价销售商品房以后，我国城镇化住房制度改革一直稳步地向前推进。1998年我国便开始了全面住房市场化改革，进一步推动了房地产市场的货币化、商品化和市场化步骤。住宅市场不断完善和日趋成熟，逐步成为国民经济新的增长点，奠定了国民经济支柱产业的地位。但房地产行业随经济的发展、物价升高等经济环境的影响，带来的高房价问题又成为另一重大经济问题。现在，面对居高不下的房价，让我国的居民们可谓是谈“房”色变！

住宅商品房的价格是住宅市场供需双方之间经济利益关系的平衡点。它不仅是商品住宅所处城市经济发展水平与商品住宅购买者收入状况的市场表现，而且也是商品住宅所处居住环境与商品住宅所在区位、商品住宅本身品质的直接反映。居高不下的住宅价格蕴藏着许多内在相互联系的信息，包括人均gdp，国民人均收入，城镇化水平，现代工业化水平，消费水平等等。房地产行业对于国民经济的拉动效应与日俱增，几乎到了“牵一发而动全身”的程度。随着房价在近几年的迅速疯涨的过程中，我国政府也是在不断要求各地区、各相关部门切实保障性住房建设和稳定房屋价格，坚决遏制部分城市房地产的过快投资和价格的非理性上涨。即便如此，一些大中城市的房价依然是在继续攀升，势头强劲，政府的调控结果不尽如人意。住宅商品房价格己经日渐成为政府、居民、开发商、学术界等各方面关注的焦点。

由于我国疆域辽阔，每个地区处于不同经济发展水平导致住宅房价格处于不同水平，而每个地区内部也因不同的地理位置使得住宅房价格也有所不同。再者，在城市商品住宅价格水平整体上涨的同时，不同区位的房价上涨幅度也不同，因此，住宅商品房价格会带有很明显的区域差异，住宅房的价格与地理空间位置有着密切的关系。

本文既是从人均gdp、工业化水平，这两个角度为切入点，选取我国除港澳台之外31个省份地区从2005年至2014年的房价数据进行空间分析。

二、房价影响因素分析

本文主要利用了工业化水平、人均gdp这两个自变量对于住宅商品房价格影响的分析。文章所用的原始数据均来自中国统计年鉴，在此基础上进行的一些公式变化。另外，本文的数据处理是在MTALAB、GeoDa、R语言这三个软件进行处理的。

1、住宅商品房的价格分析

表1是全国住宅商品房2005—2014年期间每年全国的房价，图2.1是全国房价的折线图。结合表格和图1，可以发现，全国房价变动整体上升，局部波动。2006-2007年，房价涨速较快，由3119.25元/m2上升到3645.18元/m2。而2007-2008年，房价有一个较平缓的回落，由3645.18元/m2下跌到3576元/m2。2008年以后，我国房价呈现出持续增长的态势。其中2008—2009年增幅较大，由3576元/m2上涨到4459元/m2。在2014年的房价达到最大值，为5933元/m2。

并且对于全国住宅商品房价格进行了卡方检验，结果显示其p值小于0.05，拒绝正态性假设，即全国住宅房价不服从正态分布。

2、工业化水平

工业化水平运用的是是第三产业总产值除以国内总产值得到的数值，它是国家工业化程度的度量。其发展水平往往折射出一个地区或者国家的经济状况发展水平，随着社会的发展进步，第三产业迅速发展使得其对劳动力的需求也快速提高，形成了对劳动力的巨大需求，从而对住房的需求也在上升。并且巨大的劳动力需求带来了劳动力成本上升，劳动力的工资提升，因此也增加了劳动力的实际购买力。并且第三产业，吸纳劳动力最多。它的发展往往位于城市等人口集中的地方，并且倾向于集中在某一个区域，使得这一地区的土地价格和房产价格上升，并带动周边地区的土地价格与房屋价格上升，进而对整个城市的房价上升产生影响。

图1 全国住宅商品房价格折线图

表1 全国住宅商品房价格

图2 工业化对房价的散点图

图2是2005—2014年间全国及个地区住宅房价与工业化水平之间的散点图和回归线。其计算所得的房价与工业化水平的相关系数是0.7346739，根据图3和相关系数可以知道，住宅房价与工业化水平之间相关程度较高，是明显的正相关关系。

3、人均gdp

GDP是衡量一国经济发展水平的一项基本指标，近而gdp增长速度是衡量一国经济发展速度的基本指标，他们对住房价格的影响表现在两个方面，一是随着经济的发展，gdp的增长，人们的收入提高，购买力也随之提高，从而住房价格也会上升；二是当gdp增长速度较快的年份，人们对未来预期的也会更为乐观，从而提高了购买的欲望，促进了需求，导致房价上涨。

图5是全国人均gdp增长折线图，可以直观看出2005-2014年间，人均gdp一直是在不断增长的，而且增长的速度趋于稳定。从2005年的14368元增长到2014年的47203元，增长了2.3倍，平均增幅约为3648.33元/年。图4是2005—2014年间全国及个地区住宅房价与人均gdp之间的散点图和回归线。其计算所得的房价与人均gdp之间的相关系数为0.8324223。根据图4及相关系数的结果可知，人均gdp与房价之间具有很强的正相关关系。

4、区域差异

（1）K-means聚类

K-means聚类是数据挖掘最重要的算法之一，聚类是指将一个数据集分成指定个数的类簇的过程。K-means聚类的方法是，随机选取k个初始值作为类的种子，将距离某个初始值最近的数据添加到该初始值所属的类并重新计算类的中心，通常取为重心。

图3 全国人均gdp增长折线图

图4 人均gdp对房价的散点图

（2）房价区域差异分析

工业化水平这个变量的取值在0～1之间，因此将人均gdp作极差正规化变换，使之取值在0～1之间。

运用K-means聚类，首先要知道类数，因此需要先画谱系图，确定分为几类。此操作均是在R语言中实现。所得到的谱系图如图5所示。

根据谱系结果，我们可以将其分为五类比较合适。因此建立K-means聚类的时候，选择5类。根据程序，得到聚类结果图，如图6所示。

根据图6的聚类结果，将31个省份分为五类，第一类：河北、山西、吉林、黑龙江、湖北、湖南、海南、重庆、陕西、宁夏、新疆；第二类：江苏、浙江、内蒙古、辽宁、福建、山东、广东；第三类：贵州、云南、西藏、甘肃；第四类：河南、青海、安徽、江西、广西、四川；第五类：北京、天津、上海。表2是聚类后各个类的中心。可以看出。第五类两个维度的指标都是最高的，第三类在工业化水平的类中心上为第二位，而另外三类中，第二类＞第一类＞第四类。

由于对于房价的总体分布未知，因此采用Kruskal-Wallis检验和Willcoxon秩和检验两种方法比较五类地区的房价差异。

Kruskal-Wallis检验是一个关于三组或更多数据的非参数性测试，检验样本之间是否有差异。经过检验，得到P值为0.002905.通过了5%水平下的显著性检验，因此可以认定各类地区的房价不相同.接下来利用Willcoxon秩和检验来比较五类房价之间的大小。需检验零假设：H：pri（i）大于pri（j）。其中i和j不相等，取值范围（1，5）。P值小于0.05，则拒绝假设。反之则接受假设。

图6 聚类结果

表2 聚类中心

表3 Willcoxon秩和检验

表2是检验结果，从结果可以知道。各类地区的房价顺序是：第五类＞第二类＞第一类＞第四类＞第三类。第五类是京津沪，为我国的发达地区，第二类的省份多位于我国东部沿海地带，第一类的省份我国东部地区加中部一些省份，第四类里省份多位于我中部地区，第三类的四个省份在我西部地区。总体来看，这样分类符合我国目前的经济从东部到西部递减的趋势。

三、空间面板模型构造

1、空间滞后模型

空间滞后模型是用以考察变量在地区是否有扩散现象，即溢出效应，其表达式为：

式中，Y是因变量，即扩散程度；X为n*k阶的外生解释变量矩阵；ρ为空间回归系数，反映了样本观测值中的空间依赖作用，Wy为空间滞后因变量，是一内生变量，反映了空间距离对因变量的作用；ε为随机误差向量；参数β反映了自变量X对因变量Y的影响。

2、空间误差模型

空间误差模型的数学表达式为：

式中，ε为随机误差向量，λ为n*1阶的截面因变量向量的空间误差系数，为正态分布的随机误差向量，衡量了样本观察值中的空间依赖作用。参数β反映了自变量X对因变量Y的影响。存在于扰动误差项之中的空间依赖作用度量了邻接地区关于因变量的误差冲击对本地区观察值的影响程度。

四、房价影响因素实证分析

1、基于Moran’I系数的自相关检验

（1）全局空间相关性

利用Moran’I系数对我国31个省域2005-2010年间住宅商品房价格数据做全局空间自相关检验，分析各省域之间的商品房价格是否存在空间交互作用。

表4显示了我们31个省域住宅商品房价格的Moran’I系数。我国在这连续十年的时间里，31个省域住宅房价格的Moran’I系数均小于0.01，都通过了显著性检验。这组数据说明我国区域的住宅商品房价格之间存在着显著的空间交互作用。即商品房价格在空间的布局上并不是随机分布的，而是存在着显著的空间相关关系，观察Moran’I系数发现，2005—2014年间的Moran’I系数均大于0，徘徊在0.3左右。这说明住宅商品房价格存在显著的空间正相关关系，表现为商品房价格相对较高的省域倾向于与其他商品房价格相对较高的省域相临近；商品房价格相对较低的省域倾向于与其他商品房价格相对较低的省域相临近。

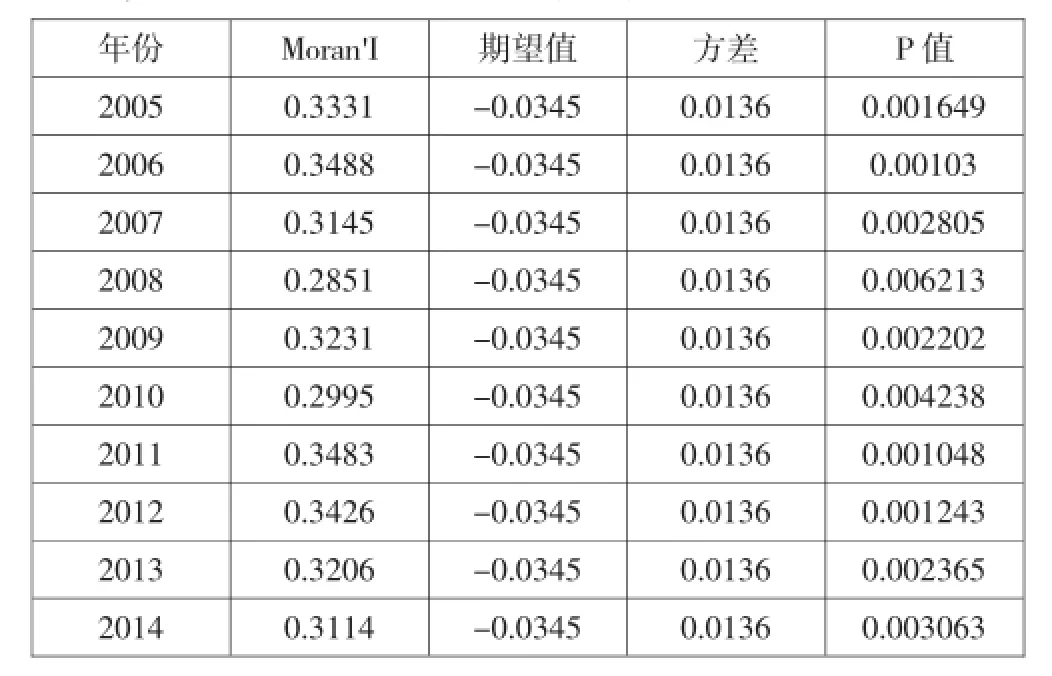
表4 我国31个省域住宅商品房价格Moran’I系数

图7 2005年、2008年、2011年、2014年Moran’I散点图

（2）局部空间相关性

引入一阶邻接“车标准”权重矩阵，通过GeoDa软件对2005-2014年我国各省域住宅商品房价格的局部空间相关性进行分析。可以运用Moran’I散点图。Moran’I散点图将各省域的商品房价格的分布划分为四个象限，第一象限（高-高）表示住房价格相对较高的省域被住房价格相对较高的其他省域所包围；第三象限（低-低）表示住房价格相对较低的省域被住房价格相对较低的省域所包围；第二象限（低-高）表示住房价格较低的省域被住房价格相对较高的哲域所包围；第四象限（高-低）表示住房价格相对较高的省域被住房价格相对较低的省域所包围。图7分别是2005年、2008年、2011年、2014年的Moran’I散点图。从图7可以看出，高-高相邻和低-低相邻的省域占据大多数。即多数省份多集中在散点图的第一、三象限。即住宅房价格较高的地区相对的趋于和住宅房价格较高的地区相邻，比如北京、天津、江苏、浙江、上海等地。住宅房价格较低的地区相对的趋于和住宅房价格较低的区域相邻，比如新疆、宁夏、甘肃等地。

1、空间面板模型分析

（1）住宅商品房价格的空间相关性检验结果

首先应当检验变量的空间相关性。本文对2005—2014年全国31个省市数据面板数据进行处理，使用MATLAB软件进行空间相关性检验，其检验结果如表5所示：

从表5可以知道，Moran’I系数为正，且P值检验为0.007988，通过了显著性水平检验，因此，认为住宅商品房价格具有空间集聚效应。

表5 Moran’I空间相关性检验结果

（2）住宅商品房空间面板数据估计结果

利用空间面板数据模型分析人均gdp、工业化水平等影响因素对住宅房价格水平的影响。首先，检验相应的非空间计量模型以确定其是否符合空间滞后模型或者空间误差模型。当非空间计量模型被拒绝时，则说明方程可能是空间滞后模型或者是空间误差模型，反之则是非空间计量模型。检验结果如表6，模型均在无固定效应下建立的。

表6 LM检验结果

根据表6的结果可以知道，应该选择空间误差模型，其LM检验值和稳健下的LM检验均通过了显著性检验。因此，接下来对空间误差模型的混合模型，地区固定效应模型，时间固定效应模型和时间地区都固定的双固定模型进行比较。比较结果如表7，其中1=“混合模型”，2=“地区固定效应模型”，3=“时间固定模型”，4=“双固定模型”。

表7 空间误差模型估计结果

根据表7，经过比较，混合模型和时间固定模型下的空间误差模型各项系数值均通过了显著性检验。比较混合模型和时间固定模型，在拟合优度和最大似然值数值上，时间固定模型均比混合模型大，说明时间固定的空间误差模型拟合性更好，因此选择时间固定的空间误差模型。

在固定时间的空间误差模型中，人均gdp的系数是0.081936，工业化水平的系数是15521.646，因此，在其它变量保持不变的条件下，人均gdp若每上升10000元，则会导致房价上升819.36元；工业化水平每上升一个百分点，则房价会上升15521.646元。由此可见，人均gdp和工业化水平对房价的影响因素比较至关重要的。

在空间误差模型中，参数λ衡量了样本观察值的误差项引进的一个区域间溢出成分，即度量了邻近地区关于住宅商品房价格误差冲击对本地区住宅房价格观察值的影响程度。在时间固定的空间误差模型中，λ=0.166978，并且其检验值为0.034017，通过5%水平下的显著值检验，因此可以显著的认为邻近地区住宅商品房价格的误差冲击对本地住宅房价有正向的影响，即住宅商品房价格存在空间溢出作用，其溢出作用强度为16.6978%。

五、结论与启示

1、研究结论

本文采用了10年间，31个省域的面板数据研究住宅商品房价格的空间相关性。首先，对全国十年间的房价进行了一个整体的简单分析，我国在这十年里房价是整体上升，局部波动。然后分别分析了人均gdp和工业化水平这两个指标对于房价的影响，二者与住房价格均有较强的正相关关系。接下来，在引进空间面板模型之前，首先对于我国各地区住宅商品房价格数据进行了整体和局部的空间相关性分析。从整体上，可以知道，10年的数据均通过了Moran’I系数检验，并且均大于0，可知，我国住宅房价具有较强的空间集聚效应，并且在时间上具有持续稳定性。从局部分析来看，大多数省份均分布在高-高和低-低区域，局部性也是比较明显的。最后，进行空间模型的拟合估计，得出结果。人均gdp和工业化水平对住宅房价都是产生正相关影响，并且结果也显示了邻近地区住宅房价的误差冲击对本地住宅房价有显著的正向影响，即住宅商品房价格存在空间溢出作用。

2、政策建议

随着我国经济的快速发展，第三产业，人均gdp都在不断的发展与提高，并从不同方面影响着我国的住房价格，同时房子作为居民生产生活的必需品，对国民经济的发展，产业结构的调整，人民生活水平的提高都有着极其重要的影响，房价的合理可以促进整个社会的稳定。然而当下，我国房价的快速上涨，渐渐突破居民的可承受范围，这将会直接影响我国经济的持续健康发展。因此，有如下几点建议：

（1）重区域间合作，以城市集群为房价调控对象。统筹区域商品房协调发展，充分发挥邻近城市优势互补的功能，实现区域商品房市场的融合发展，带动区域房地产市场的稳定、健康发展。

（2）一步提高城镇居民的收入水平，提升居民的房地产市场支付能力，缓解房地产市场供求失衡。

（3）市场为主，调控为辅。竖持市场机制和政府调控相结合，解决住房价格过高。充分发挥政府对市场的宏观调控、监管和住房保障职责，保障市场的合理发展。

[1] 范新英：中国城市房价的空间非线性机理研究[D]．山西财经大学，2015．

[2] 谷兴、周丽青：基于地理加权回归的武汉市住宅房价空间分异及其影响因素分析[J]．国土与自然资源研究，2015（03）．

[3] 杜小薇：我国城镇化对房价影响分析[D]．重庆工商大学，2015．

[4] 张凌：城市住房价格波动差异及连锁反应研究[D]．浙江大学，2008．

[5] 赵自胜：城市商品住宅价格空间分异研究[D]．河南大学，2010．

[6] 程华靖：我国住房价格影响因素研究[D]．西南大学，2013．

[7] 郑晓燕、周鹏：武汉市房价的空间分布格局及其影响因素分析[J]．国土与自然资源研究，2016（02）．

[8] 公言常：基于面板数据的房价空间溢出效应研究[D]．华南理工大学，2015．

[9] 吴玉鸣：空间计量经济模型在省域研发与创新中的应用研究[J]．数量经济技术经济研究，2006（5）．

（责任编辑：冷丽）