三角模糊层次分析法在高校实验室评估中的应用

李 丽

(河南职业技术学院 汽车工程系, 郑州 450046)

三角模糊层次分析法在高校实验室评估中的应用

李 丽

(河南职业技术学院 汽车工程系, 郑州 450046)

实验室评估是高校实验室建设与管理的一项重要工作，对提升实验室建设水平具有重要作用。针对目前高校实验室评估工作的现状和存在的问题，提出采用三角模糊层次分析法对高校实验室进行评估。根据高校实验室的发展目标和评估标准，建立了高校实验室的2级评估指标体系，共包括7项1级指标与35项2级指标。介绍了三角模糊数的定义与运算法则等相关基本理论。给出了基于三角模糊层次分析法的实验室评估步骤，并详细论述了指标权重矩阵的确定方法。最后，通过应用实例对该方法进行了验证。结果表明，三角模糊层次分析法在高校实验室评估中具有较好的可行性和实用性。

实验室评估； 三角模糊数； 模糊层次分析法； 指标体系

0 引 言

实验室是高校培养学生实践动手能力和创新精神的重要场所，是加强学生素质教育的重要基地。为了适应高校优化育人环境、提高教学质量的要求，促进实验室的建设与发展，有必要采用科学的评价方法对实验室进行客观的评价。实验室评估是实验室建设与管理的一项重要工作，对于优化资源配置、提升实验室建设水平具有重要作用，因此实验室评估工作越来越引起相关教育管理部门、学校职能单位以及广大实验室工作者的重视[1-8]。

目前，实验室评估通常采用百分制打分法、层次分析法、多层次模糊综合评判法、灰色局势决策法、变权综合法等，均在一定程度上取得了较好的效果。但是，在减小不确定性带来的误差、降低人为主观因素的影响等方面，仍然存在进一步改进和提高的空间。三角模糊层次分析法将三角模糊数理论与模糊层次分析法结合起来，以三角模糊数代替常规层次分析法中的标度，对评价对象采用自然语言进行单因素模糊评价，对多层次评价指标的权重采用模糊层次分析法进行判断[9]。该方法已经在企业知识管理水平评价[9]、风险量化[10]、设计方案评价[11]等问题中进行了应用，并获得了比较满意的效果。鉴于此，本文提出采用三角模糊层次分析法对高校实验室进行评估，以进一步提高评估结果的科学合理性。

1 实验室评估指标体系

根据教育部制定的《高等学校基础课教学实验室评估办法和标准》、《高等学校专业实验室评估标准(试行)》等文件，并结合各高校多年来在实验室评估工作中的经验[12-13]，本文设计了高校实验室的评估指标体系(见表1)。该指标体系共分2级，第1级指标包括7项：体制与管理、仪器设备、实验任务、实验队伍、环境与安全、规章制度、特色与创新。每个1级指标又包括若干个2级指标，共计35个。

2 三角模糊数的基本理论

2.1 三角模糊数的定义

三角模糊数能够将模糊的不确定语言变量转换为确定的数值，在相关的评价方法中可以很好的解决评价对象性能无法准确量化，而只能用自然语言进行模糊评价的问题。三角模糊数定义如下[14]：

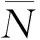
(1)

2.2 三角模糊数的运算法则

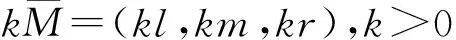
表1 实验室评估指标体系

1级指标2级指标体制与管理X1管理体制X11管理机构X12管理手段X13建设规划X14保障机制X15仪器设备X2仪器设备配置与管理X21低值耐用品管理X22贵重仪器设备管理X23仪器设备维修与完好率X24仪器设备更新X25仪器设备使用率X26实验任务X3实验教学任务X31实验考试和考核X32实验项目管理X33实验教材建设与选用X34实验开出率X35实验报告X36实验研究与成果X37科研任务与社会服务X38实验队伍X4教学师资X41队伍结构及合理性X42职责分工X43人员培训X44人员聘任与考核X45环境与安全X5学生实验用房X51设施与环境X52环境保护X53安全措施X54规章制度X6仪器设备管理制度X61安全与环保制度X62学生实验守则X63工作档案管理制度X64特色与创新X7实验室特色X71实验教学改革X72创新成果X73

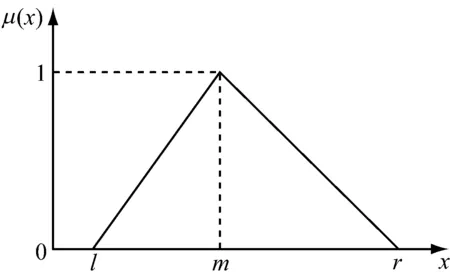
图1 三角模糊数的隶属函数

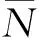
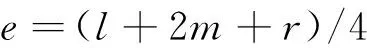
(2)

3 三角模糊层次分析法的步骤

三角模糊层次分析法的步骤如下：

(1) 建立多层次评估指标体系。模糊综合评价的第1步就是建立多层次评估指标体系，列出影响评估对象的相关因素。高校实验室的评估指标体系由7个1级指标和35个2级指标构成(见表1)。

(2) 建立评价集合。评价集合是评估专家对评估对象各项指标的直接描述。采用基于集合的三角模糊数定义方法[9]，建立了针对实验室的专家评价语言集合及其对应的三角模糊数(见表2)。

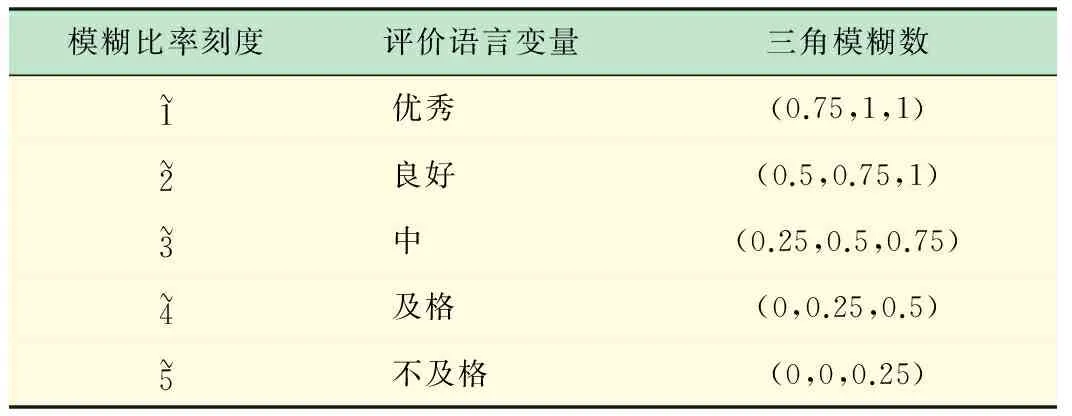
表2 评价集合及对应的三角模糊数

(3) 对1级指标X1中的2级指标X1i分别进行单因素评价，得到X12级指标的三角模糊数评价结果矩阵G1。

(4) 确定X1的2级指标权重矩阵。在模糊综合评价中，指标权重是非常重要的。采用模糊一致

判断矩阵法确定评价指标的权重，能够在最大程度上消除主观因素的影响[4]。

① 构造两评价指标X1k和X1v相对重要程度的标度表示方法，如表3所示。

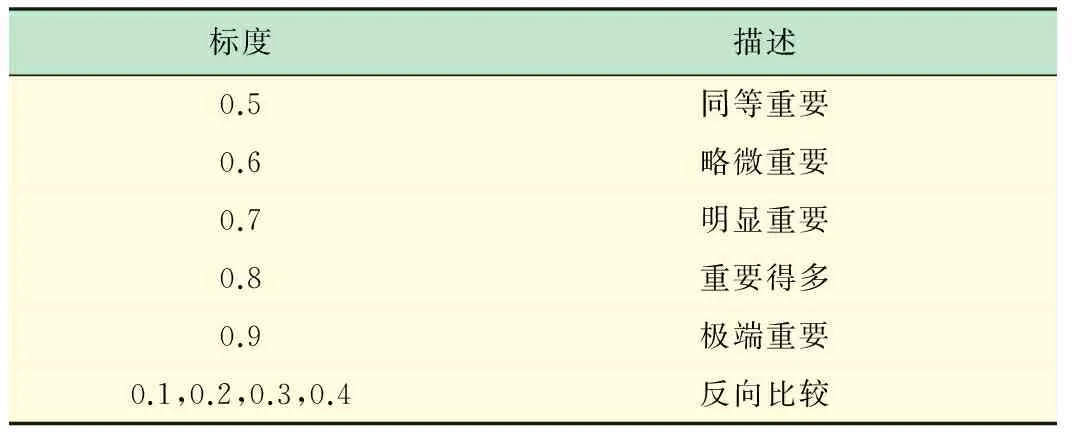
表3 评价指标相对重要程度的标度

② 利用表3，将X1的2级指标两两比较，得到2级指标的模糊互补判断矩阵P1。

③ 运用文献[15]中的数学变换方法，将P1改造为模糊一致矩阵M1；求出M1的最大特征值及特征向量，并进行归一化处理，得到归一化的特征向量H1，即为X1的2级指标权重矩阵。

(5) 将X12级指标的评价结果矩阵与权重矩阵进行模糊运算，得到1级指标X1的评价结果三角模糊数

(3)

式中，符号⊕和⊗分别表示模糊数运算的加法和乘法。

(6) 按照上述步骤，计算得到全部1级指标的评价结果三角模糊数，构成矩阵

(4)

(7) 利用步骤(4)的方法，确定1级指标权重矩阵

(5)

(8) 将1级指标评价结果矩阵R与权重矩阵W进行模糊运算，得到综合评价结果三角模糊数

(6)

若有多个专家参与评估，则需要将所有专家的评价结果求算术平均数[16]。

4 应用实例

为了更好的提升实验室建设水平，某高校实验室管理处组织了3位专家(Exp1～3)对该校的4个工科实验室(Lab1～4)进行评估。在评估过程中，建立了多层次的高校实验室评估指标体系(见表1)和专家评价语言集合(见表2)，采用了本文的三角模糊层次分析法，具体步骤如下。

(1) 对1级指标X1的5个2级指标分别进行单因素评价，得到的三角模糊数评价矩阵如下：

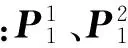
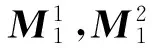
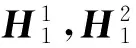
(3) 将X1的2级指标评价矩阵与权重矩阵进行模糊运算，得到X1的三角模糊数评价结果如下：

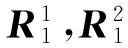
(4) 按照上述步骤，计算得到全部1级指标的三角模糊数评价结果如下：

(5) 利用2级指标权重的确定方法，得到1级指标的权重矩阵如下：

W1=[0.114, 0.155, 0.164, 0.139, 0.174, 0.116, 0.139]T

W2=[0.112, 0.155, 0.168, 0.141, 0.174, 0.120, 0.130]T

W3=[0.120, 0.159, 0.153, 0.141, 0.170, 0.122, 0.135]T

W1、W2与W3分别为3位专家针对1级指标给出的权重。

(6) 将上述步骤(3)与步骤(4)所得的全部1级指标的三角模糊数评价结果，组成新的矩阵，再与1级指标权重矩阵进行模糊运算，得到综合评价结果。

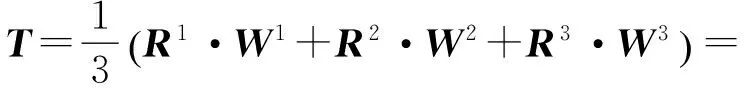
(7) 对综合评价结果进行去模糊值处理，可得：

T=[0.646, 0.552, 0.734, 0.489]T

根据以上结果及最大隶属度原则可知，4个实验室的评估等级分别为：Lab1(良)、Lab2(中)、Lab3(良)、Lab4(中)，且排序为：Lab3>Lab1>Lab2>Lab4。结果表明，实验室Lab3的建设与管理情况要强于其他实验室。体现在它的仪器设备管理较好，实验队伍实力较强，规章制度完善，特色鲜明，创新成果显著等方面，与实际情况相符。而实验室Lab2和Lab4则需要在实验任务、环境与安全、规则制度等方面进一步改进与提高。

5 结 语

高校实验室评估是实验室管理中的一项重要工作。本文建立了实验室评估的二级指标体系，并采用三角模糊层次分析法对高校实验室进行评估，该方法将三角模糊数理论与模糊层次分析法结合起来，使评估结果更加科学、合理与准确，并且易于通过计算机编程实现，具有较好实用性。通过实例应用，评估结果与

实际情况相符，证明了三角模糊层次分析法在高校实验室评估中的可行性和实用性。

[1] 唐 岚，甄洪鹏，谢庆春，等. 构建高校实验室效益评估指标体系的探究[J]. 实验技术与管理, 2013, 30(5): 185-187, 199.

[2] 侯亚彬，张 慧，丁 颖. 高校教学实验室综合效益考核的评估实践与思考[J]. 实验技术与管理, 2012, 29(6): 197-199.

[3] 苏文霞，白 琳，王明东. 基于灰色局势决策的实验室工作水平评估[J]. 实验室研究与探索, 2011, 30(8): 206-209.

[4] 陈念东，邹丽云. 多层次模糊综合评价法在高校教学型实验室评估中的应用[J]. 赤峰学院学报(自然科学版), 2011, 27(10): 215-218.

[5] 刘鹏超，张喜刚. AHP-模糊综合评价法在高校科研实验室评估中的应用[J]. 中国电力教育, 2011 (10): 134-135.

[6] 樊 敏，宋世军. 变权综合算法在高校实验室工作质量评估中的应用[J]. 实验技术与管理, 2008, 25(3): 159-161.

[7] 苏文霞，王战伟. 实验室工作水平的模糊综合评估[J]. 实验室研究与探索, 2006, 25(6): 722-724.

[8] 张 黎. 高校建筑模型实验室的安全风险评估[J]. 实验室研究与探索, 2013, 32(5): 239-241.

[9] 潘 星，王 君，刘 鲁. 航空制造企业知识管理水平的模糊综合评价方法[J]. 计算机集成制造系统, 2007, 13(10): 2019-2026.

[10] 朱松岭，周 平，韩 毅，等. 基于模糊层次分析法的风险量化研究[J]. 计算机集成制造系统, 2004, 10(8): 980-984.

[11] 古莹奎，杨振宇. 概念设计方案评价的模糊多准则决策模型[J]. 计算机集成制造系统, 2007, 13(8): 1504-1510.

[12] 李 毓. 基于模糊层次决策的高校实验室综合评估模型[J]. 实验室科学, 2011, 14(5): 152-157.

[13] 宗军君，叶结松，侯智斌，等. 模糊可拓层次分析法在实验室评估中的应用[J]. 实验室研究与探索, 2012, 31(3): 196-200.

[14] 王 宇，尚 利，汪永超，等. 基于FAHP的服务型制造企业供应商的选择研究[J]. 组合机床与自动化加工技术, 2015 (11): 149-152, 156.

[15] 刘 怡，张子刚. 基于模糊层次分析法的工作流任务排序研究[J]. 计算机集成制造系统, 2006, 12(5): 688-691,701.

[16] 张东方. 基于FAHP 的立体车库人机界面可用性评价方法[J]. 机械设计, 2014, 31(4): 97-100.

Application of Triangular Fuzzy Analytic Hierarchy Process in Evaluation of University Laboratories

LILi

(Department of Automobile Engineering, Henan Polytechnic, Zhengzhou 450046, China)

Laboratory evaluation is an important work of university laboratory construction and management, and it plays an important role to enhance the level of laboratory construction. In the light of the present condition and existing problems of laboratory evaluation in colleges and universities, the triangular fuzzy analytic hierarchy process (AHP) was adopted. According to the development goal and evaluation standards of laboratories in colleges and universities, an evaluation index system of laboratory including seven first grade indexes and 35 second grade indexes was established. The related basic definition of triangular fuzzy number and algorithm principles were introduced. The laboratory evaluation steps based on triangular fuzzy AHP were given, and the determination method of index weight matrix was described in detail. Finally, an application example of this method was verified. The results showed that the laboratory evaluation method based on triangular fuzzy AHP has good feasibility and practicability.

laboratory evaluation; triangular fuzzy numbers; fuzzy analytic hierarchy process; index system

2016-07-28

河南省高等学校重点科研项目(16A413015)；河南职业技术学院科研基金资助(2015-HZK-04)

李 丽(1982-)，女，安徽无为人，硕士，讲师，主要从事企业信息化、数字化设计的研究。

Tel.：15039094960; E-mail:cflw2006@163.com

G 482

A

1006-7167(2017)03-0255-05