基于遗传计算模糊PID的数字随动系统设计

赵文龙， 黄 寻

(南昌航空大学 信息工程学院， 南昌 330063)

基于遗传计算模糊PID的数字随动系统设计

赵文龙， 黄 寻

(南昌航空大学 信息工程学院， 南昌 330063)

开发了以TMS320F28335为主控芯片的数字随动系统控制器，实现了遗传计算模糊PID控制算法在微控制器上的应用。上位机软件采用MFC程序设计编写，实现控制器与PC机的串行通信，将给定量与反馈量在PC机上进行波形和形态显示，便于更直观地对其控制性能进行分析。实验结果表明，实际控制效果与Matlab仿真有一定的差距。遗传计算模糊PID控制与PID控制相比较，系统的稳态性能增强，动态性能减弱。仿真与真实系统的对比可以使学生对理论与实际有更加直观的认识和深入的理解，能够取得良好的学习效果。

数字随动系统； 数字信号处理器； 遗传计算； 模糊PID； 复合控制

0 引 言

数字随动系统是一个由计算机控制的位置跟踪系统，它将计算机预先给定的在时间上不连续的数字量变成在时间上连续的，并且有一定输出功率的模拟量。当给定数字量发生变化时，输出的模拟量也随之发生变化。文献[1-2]中设计了以STC单片机为核心的控制器，实现多种控制规律的数字位置随动控制，控制方法主要以传统PID为主。文献[3-8]中采用Matlab仿真方法对模糊控制算法及参数的选定进行研究，为随动系统的深入研究奠定了理论基础。文献[3]中采用模糊控制算法，文献[4,6-8]中采用了模糊自适应PID控制算法，文献[5]中采用模糊积分控制算法。以上这些研究仅仅停留在软件仿真层面，在教学中不能提供给学生一个真实的控制效果和直观的感受。

为了使学生对经典控制和智能控制有一个真实的感受，本文将遗传计算模糊PID控制算法在微控制器上进行了实现。采用运算速度快、外设资源丰富的TMS320F28335作为主控芯片设计了数字随动系统控制器。为了更方便地分析其控制性能，设计了上位机软件实时显示给定轮盘和反馈轮盘的图形跟踪效果和给定和反馈数据的波形曲线，可以更加直观地表达其控制效果。

1 数字随动系统的设计

1.1 位置随动系统原理

位置随动系统是典型的位置闭环反馈系统，一般随动控制系统要求有良好的跟随性能。输出响应的快速性和准确性成了位置随动系统的主要特征。数字随动系统结构图如图1所示。其中，C0为给定的数字量；θ为反馈的位置数字量。

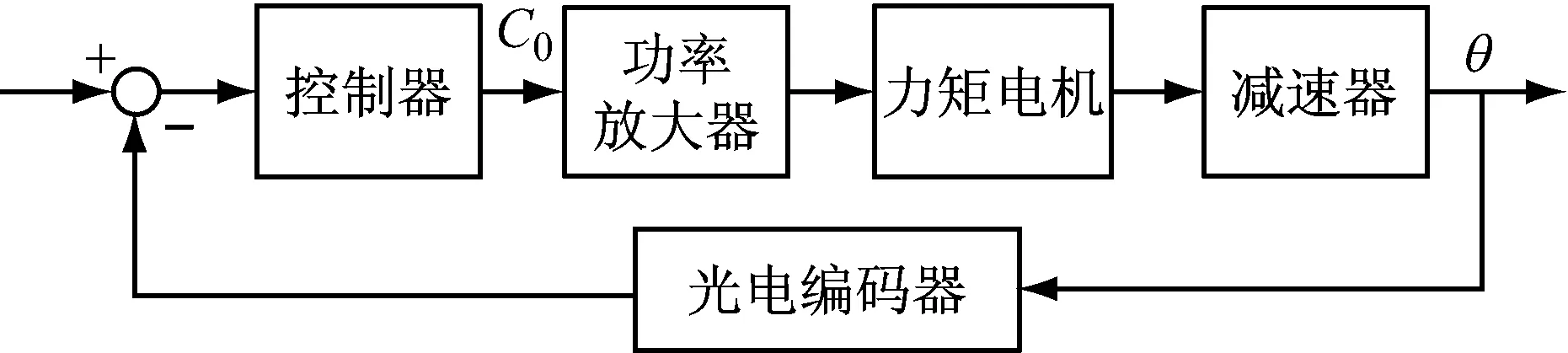
图1 数字随动系统结构图

1.2 DSP控制器的设计

控制器采用TMS320F28335作为核心处理器，辅以外围电路，构成嵌入式随动系统控制器。ADC单元对给定的电压信号进行数字量转换，9位I/O口采样光电编码器脉冲信号，作为系统的反馈。处理器通过串口或USB口实时与PC机进行通信。此控制器主要由以下几个模块组成：TMS320F28335最小系统、电源系统电路、ADC信号调理电路、数码管显示电路、功率放大电路、声光报警电路，总的硬件控制系统结构图如图2所示。

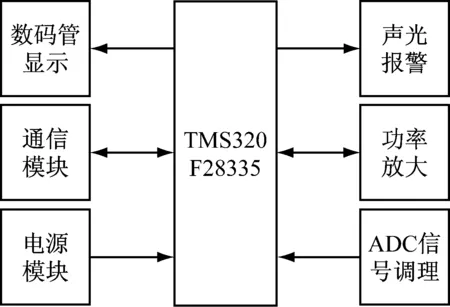
图2 控制器硬件系统结构图

软件完成数据采集和处理、信息显示、数据通信以及控制算法。采用模块化编程思想，各模块进行独立编程。首先进行子程序设计，包括数码管扫描显示、A/D转换、串行通信、数据滤波，其次进行相应的控制算法设计，如遗传优化、PID控制算法、模糊控制算法，最后运用前面设计的子程序以及控制算法进行位置随动系统综合程序设计。位置随动系统主程序流程图如图3所示。

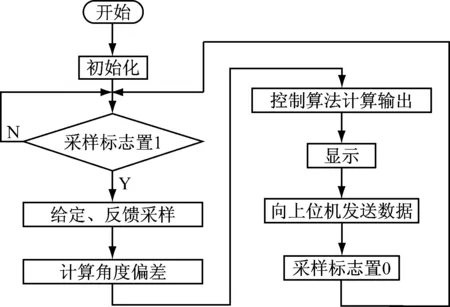
图3 位置随动系统主程序流程图

1.3 上位机软件设计

上位机软件采用MFC程序设计编写，实现控制器与PC机的串行通信，将数据在PC机上进行波形显示和形态显示，具有良好的人机交互界面和完整的数据分析能力。通过向被测随动系统发送测试信号来检测被测随动系统的动静态特性。数字随动系统实物照片如图4所示。

图4 数字随动系统实物图

2 控制器原理与遗传计算

模糊控制器通常由以下几部分组成：模糊化、数据库、规则库、模糊推理和清晰化。其中，模糊化、模糊推理、规则库和清晰化过程通过离线模糊计算产生控制表，提供给在线实时控制使用。理论分析和实验都表明，只利用模糊控制器进行系统控制，往往不能满足控制对象的所有指标(尤其是在控制底层)，所以一个完整的模糊控制系统还需要某种传统的控制器作为补充，一般采用的就是PID控制方法。

为了使模糊PID控制器[9]具有更好的性能，控制参数需要根据动态和稳态性能不断的调整参数，其调整方法主要包括[10]：控制规则调整、隶属函数调整、系数调整。该3种方法中，对系数调整来改变控制器性能较其他两种方法要简单得多。模糊控制器的系数主要有量化因子和比例因子。由于同时调整两种因子会使控制算法过于复杂，且比例因子的因果关系较明确，最终也能起到调整量化因子的作用，故只需对比例因子进行在线整定即可。

将模糊推理和清晰化过程用遗传算法进行替代，可以使控制量和比例因子同时确定，节省比例因子的整定时间。控制系统结构如图5所示。

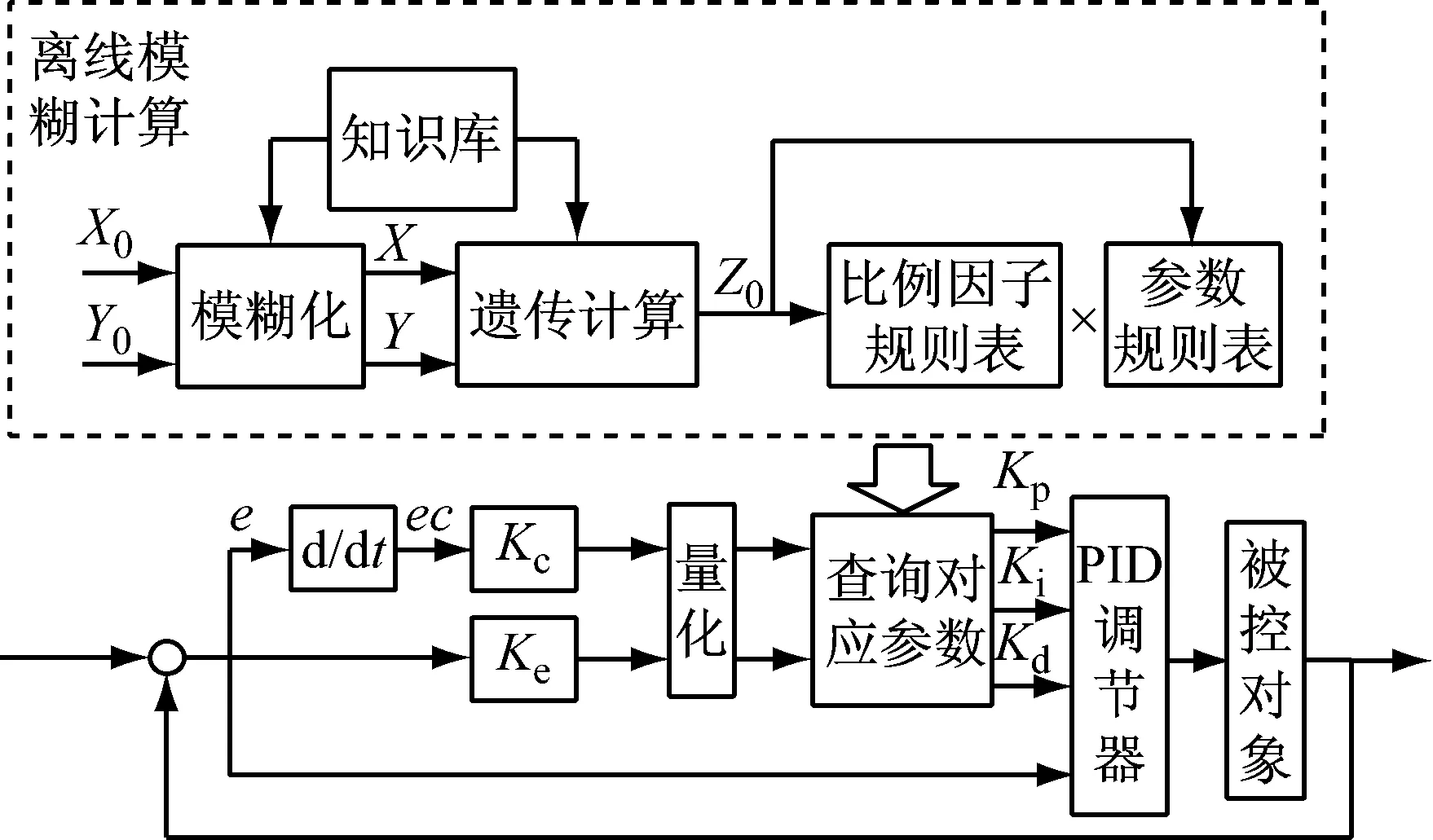
图5 控制系统结构图

2.1 模糊控制

从模糊控制器实现的难易程度与其控制性能的优良性上考虑，二维模糊控制器是最好的选择。常用的二维模糊控制器都是以系统误差e和误差变化率ec作为输入变量。

(1) 模糊化及隶属函数的确定。采用双输入三输出模糊控制器设计。以给定转角C0与反馈转角θ的偏差e及偏差变化率ec作为系统的输入变量；将后级PID控制器的3个给定参数Kp、Ki、Kd作为输出变量，比例因子qp、qi和qd对应于不同的输入量时具有不同的数值。

输入变量和输出变量的模糊子集语言变量均为{NB,NM,NS,NZ,PS,PM,PB}。其模糊子集的隶属度函数取梯形函数和三角函数，分别关于y轴和x=5对称，如图6所示。

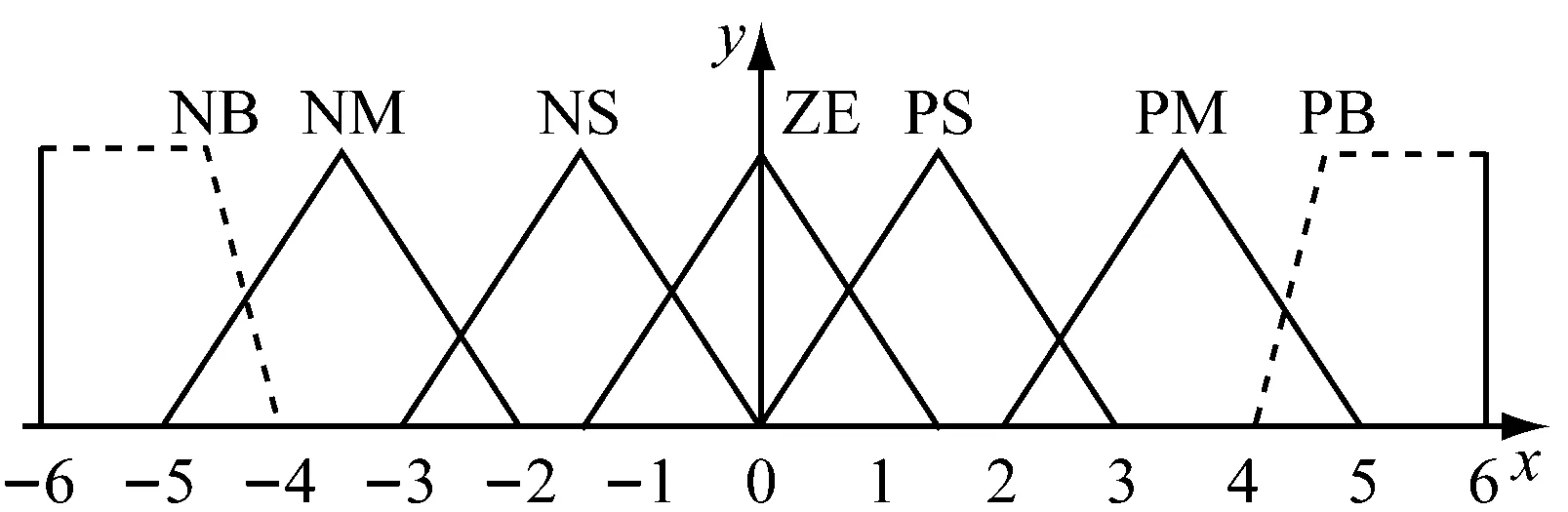
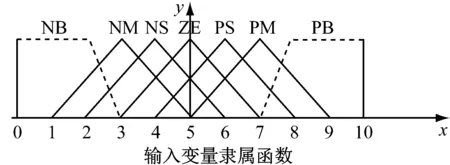
图6 隶属度函数示意图

(2) 模糊规则的建立及确定输出量。根据控制经验，PID参数的调整规则见表1[11]。在确定精确输出量时，通常需要根据制定的模糊规则进行模糊推理得到模糊关系，然后根据输入的模糊量得到一个模糊解集，再对模糊解集进行清晰化处理得到一个精确解。本文提出一种利用遗传计算方法代替模糊推理及解模糊来直接确定精确解及其对应的比例因子的方法。即根据输入量和模糊规则确定了输出量的模糊等级后，在相应的区域进行计算，确定精确解及对应比例因子。

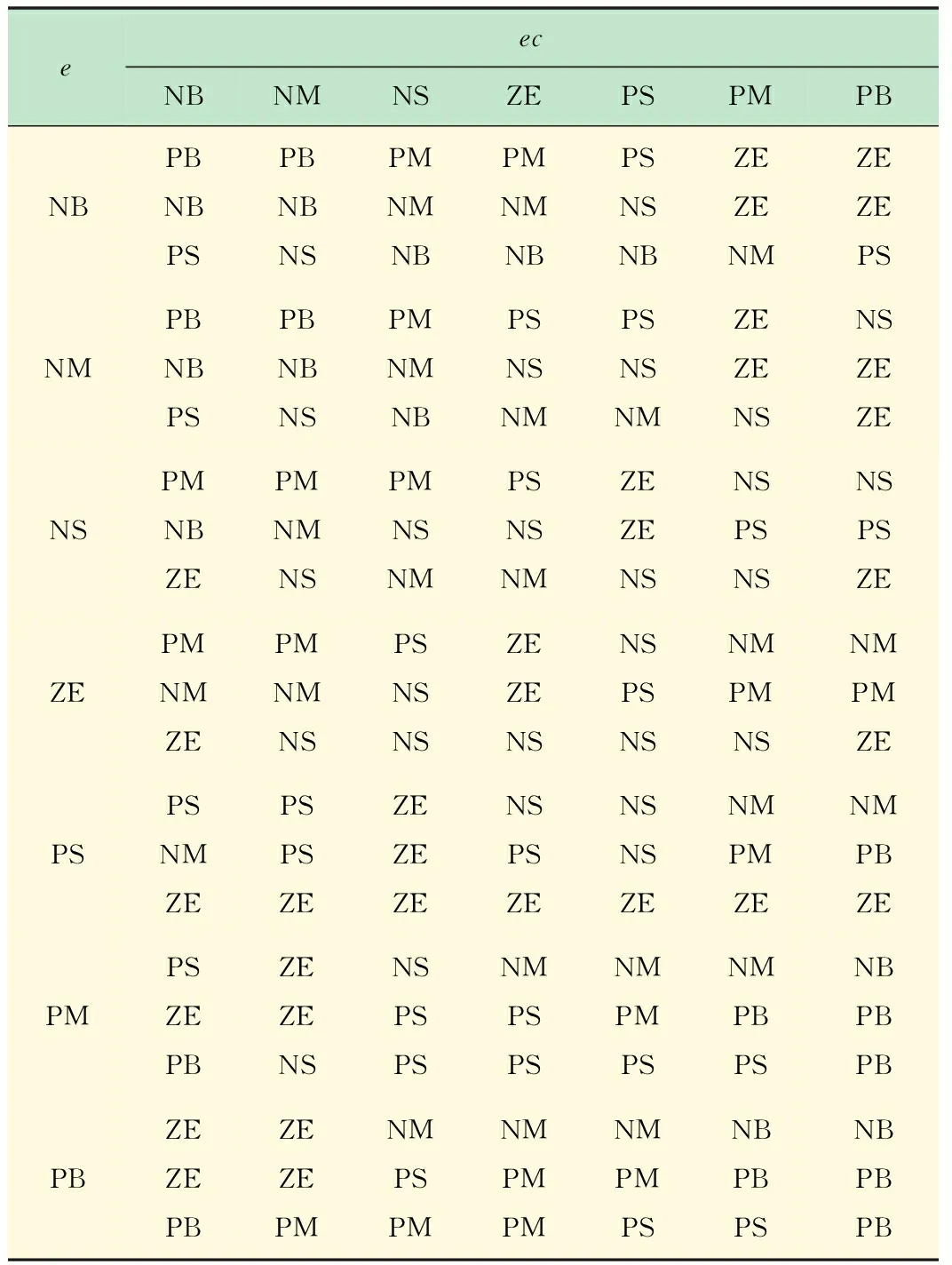
表1 模糊控制规则表

2.2 遗传计算

在求解问题时,遗传算法首先要选择编码方式,它直接处理的对象是参数的编码集而不是问题参数本身,搜索过程既不受优化函数连续性的约束,也没有优化函数微分必须存在的要求。因此，参数的选择和编码方式十分重要[12]。

通常需要根据实际控制效果来调节对应的比例因子，比例因子的确定主要靠专家的经验或反复试探的方法来调整，这实际上是一个寻优的过程。

(1) 编码。本文采用实数编码，该方法的优点是便于全局搜索，防止陷入局部最优，提高运算效率。决策变量有：Kp、Ki、Kd、qp、qi和qd。将每一个决策变量当做一个基因组成一条染色体，其结构如图7所示。

图7 染色体结构图

由模糊控制规则表可知，共有49条模糊控制规则，每条控制规则对应一条最优染色体。Kp、Ki、Kd的取值范围为所对应的模糊等级隶属函数范围；qp、qi、qd范围为[0,2]，精度为小数点后2位。

(2) 适应度函数。考虑到性能指标应当既能反映动态性能，又能包含稳态特性，选择误差绝对值乘以时间的积分作为寻优的性能指标[13]：

(1)

为了适用计算机运算，将上式离散化得

(2)

为了避免超调，可以采用惩罚功能，即一旦产生超调，就将超调量作为最优指标的一项[14]：

(3)

e(t)<0

式中，K1、K2为权值。

由于遗传算法要求个体适应度越大越优，且通常优良参数对应的性能指标值较小，故须将性能指标函数转换为趋近于1的适应度函数。转换函数为

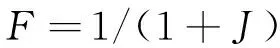
(4)

(3) 遗传算子。选择：选择算子采用无回放余数随机选择，该方法可以确保适应度优于均值的个体遗传到下一代，误差较小。

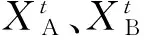
(5)

式中，t为进化代数。

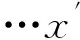
(6)

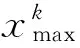
(7)

式中：r∈[0,1]，为符合均匀概率分布的一个随机数；T为最大进化代数；b为系统参数，它决定随机扰动对进化代数t的依赖程度。

(4) 控制参数。遗传算法中的交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在。为了得到一个较好的数值，本文采用自适应遗传算法，Pc和Pm计算表达式如下：

(8)

(9)

式中：fmax为群体中最大的适应度值；favg为每代群体的平均适应度值；f′为要交叉的2个个体中较大的适应度值；f为要变异个体的适应度值。

3 仿真与实验

3.1 被控对象的仿真模型

通过对被控对象的建模，可以得到被控对象为一比例积分双惯性模型，其数学表达式为：

(10)

进行拉氏反变换可以得到系统的微分方程：

40u(t)

(11)

通过计算机使用四阶龙格库塔法求出被控对象的输出响应。

3.2 参数的遗传优化选择

首先需要确定一个具体的PID参数值，根据经验给输出变量和比例因子一个合理的搜索寻优范围，根据搜寻结果的适应度值进行范围缩小，直到寻找到符合期望的一组PID参数。图8所示为根据性能指标式所进行参数选择的输出响应曲线。所算得PID参数为：Kp=10.3，Ki=5.76，Kd=0.42。

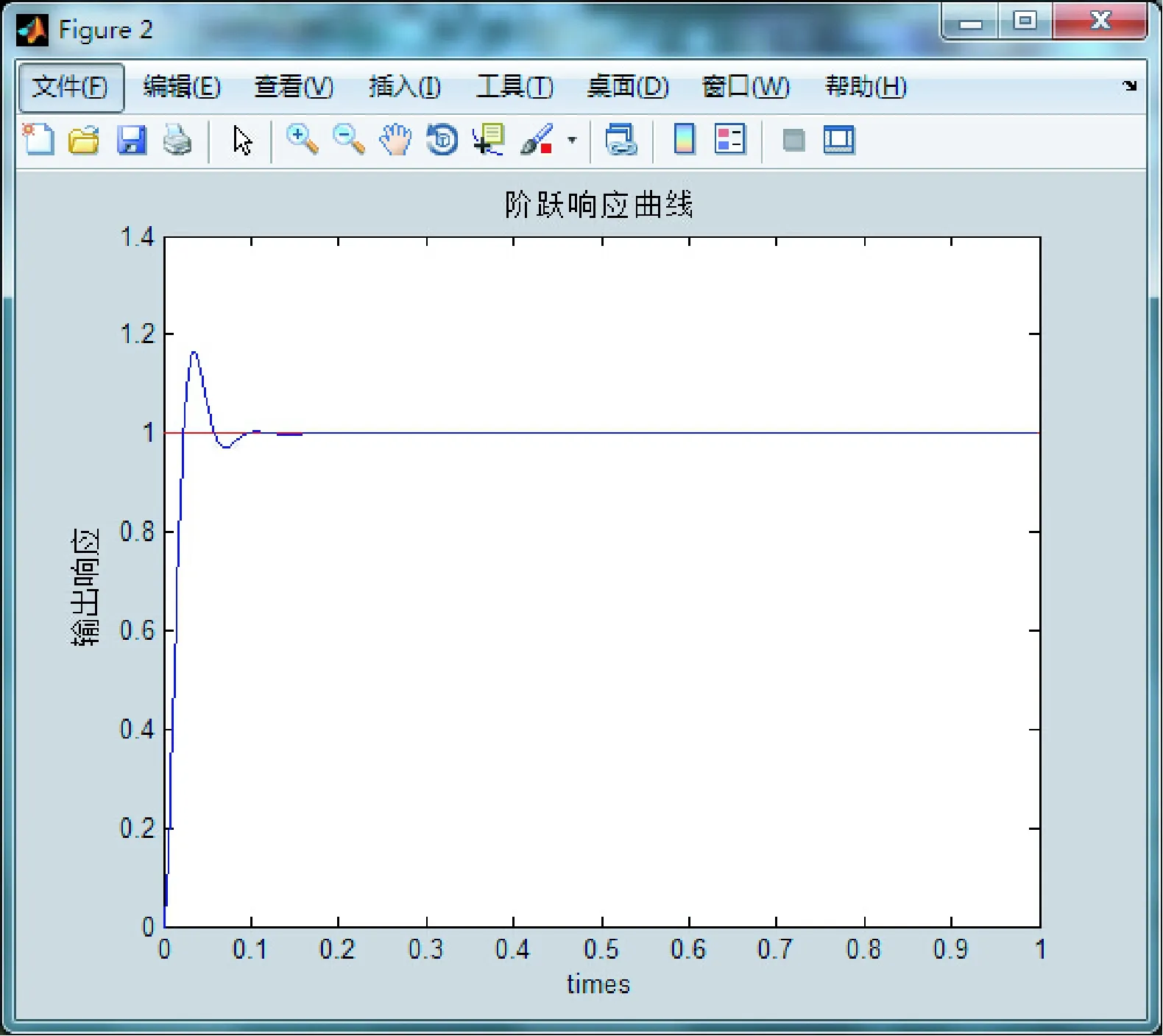
图8 输出响应曲线

从图8可以看出，虽然输出具有良好的响应速度，但有超调，因此，在根据模糊控制规则表和隶属函数遗传优化计算控制量查询表时，采用超调惩罚性能指标。通过计算，可以得到PID参数查询如表2所示。

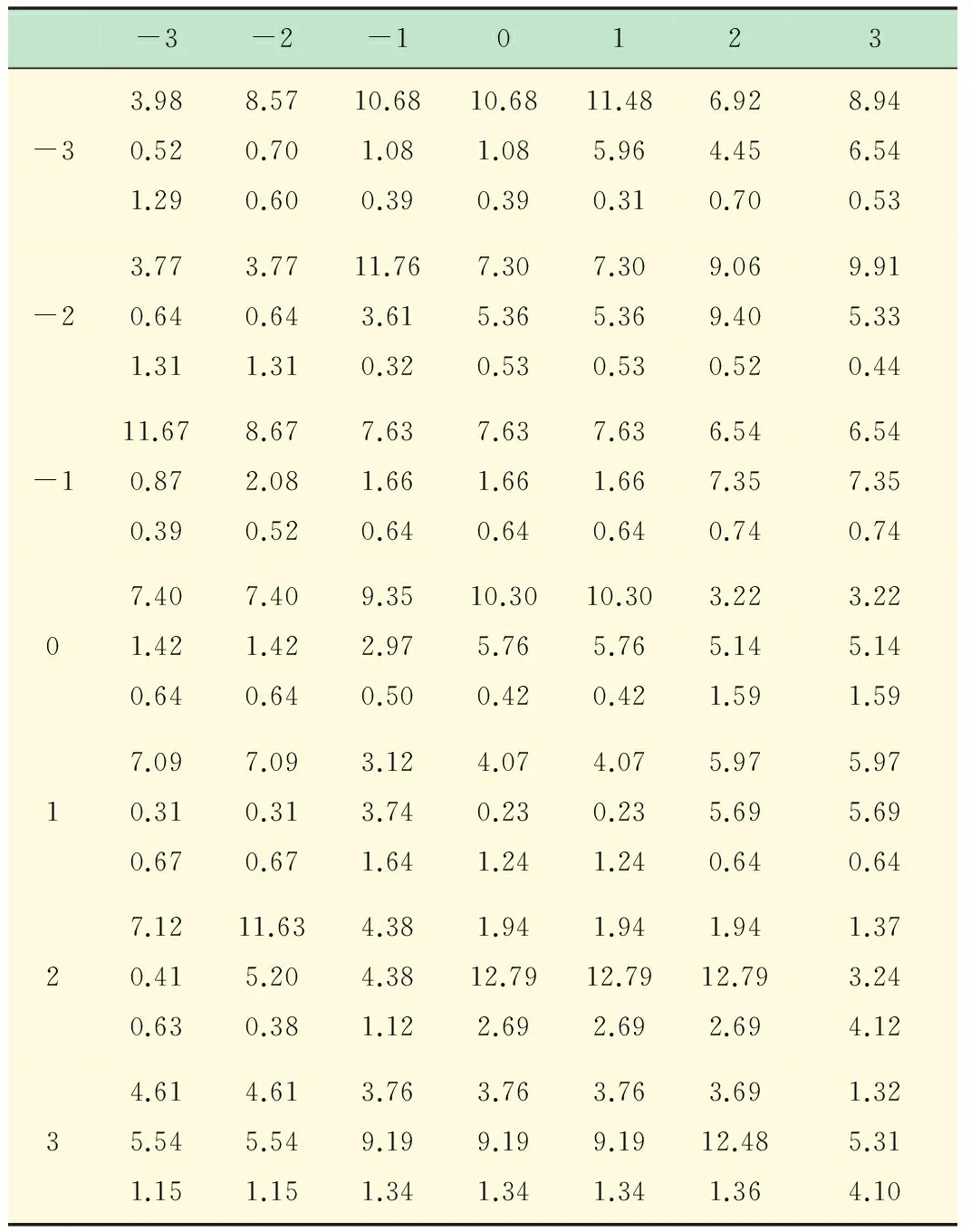
表2 控制参数查询表

3.3 仿真结果

根据图5系统结构图搭建仿真，给定信号为幅值为1的阶跃信号，图9所示为仿真结果。

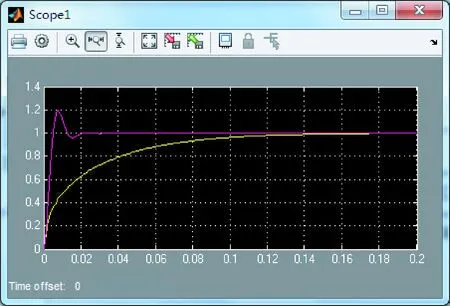
图9 输出响应曲线

图中粉色曲线为PID控制响应曲线；黄色曲线为模糊PID控制响应曲线。可以清楚看到，模糊PID响应无超调，但到达稳态时间加长了许多。

3.4 实验验证

为了验证随动系统模糊PID控制算法在DSP控制器上的可行性及效果，将它与PID控制算法在真实被控对象上进行对比。

首先进行PID控制。给定量分别为50°～-100°及-100°～50°的阶跃信号，实验结果如图10所示。

然后进行模糊PID控制，给定量和控制方式不变，实验结果如图11所示。

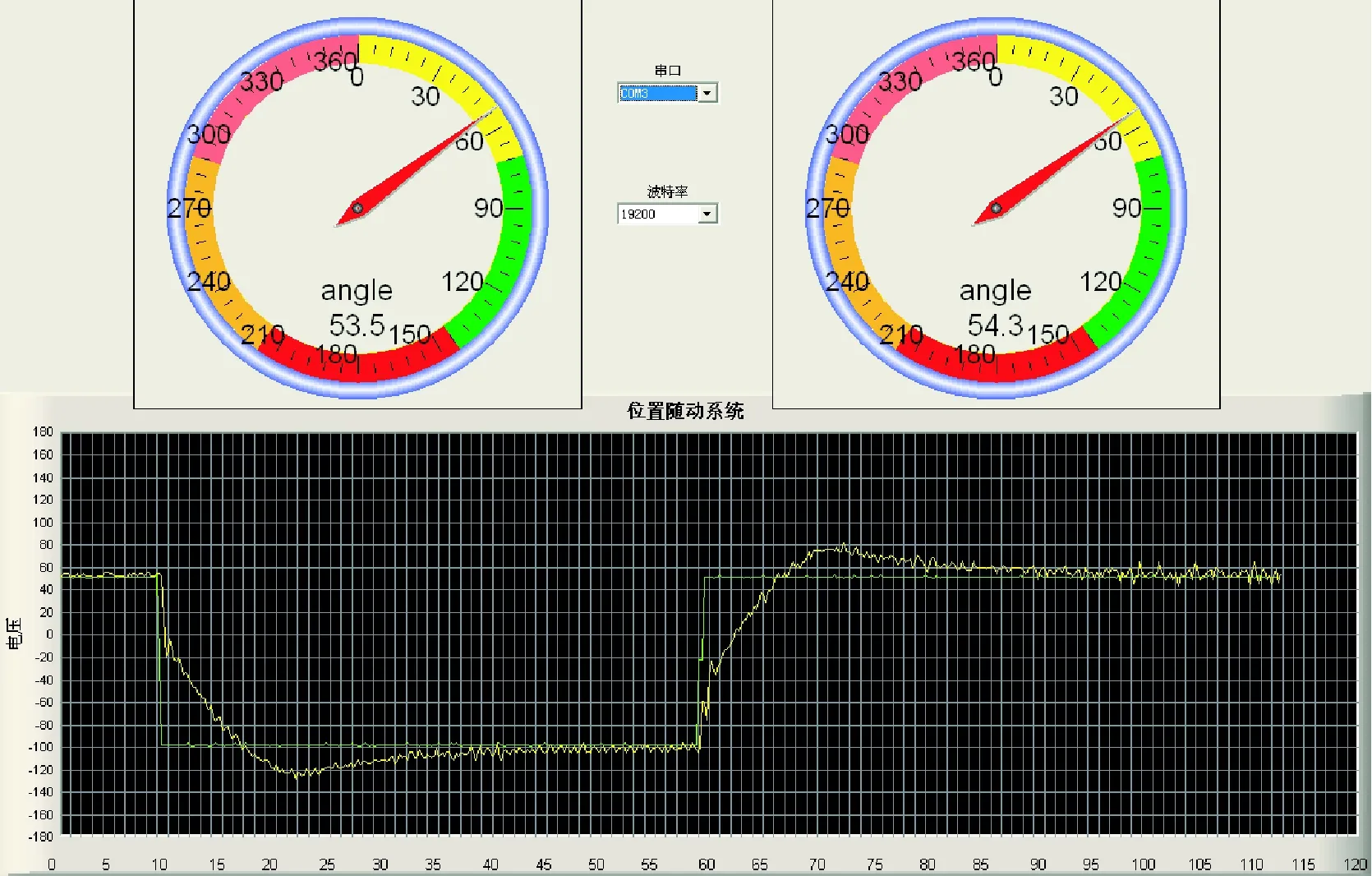
图10 阶跃给定时PID控制实验结果图

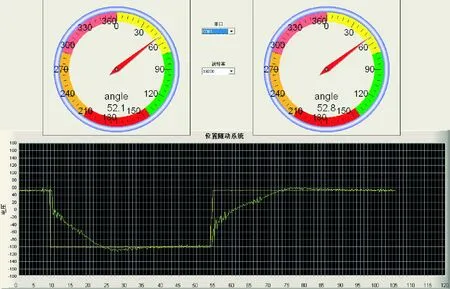
图11 阶跃给定时模糊PID控制实验结果图

从图中波形对比可以看出，真实实验结果与仿真结果大体一致，从而验证了控制算法的可行性。观察两组波形可以发现，在PID控制下，电机对正反两个阶跃信号的响应曲线具有完美的对称性，说明PID控制在正反两个方向上的控制效果一致性好。而模糊PID控制正反两个方向上的响应曲线有偏差，正方向的多项时间指标都比负方向大，说明在正反两个方向上的控制效果不一致。在上升时间初期，波形抖动持续时间比PID控制长。

为了进一步定量分析两种控制方式的性能，将实验结果进行反色放大，如图12、13所示。

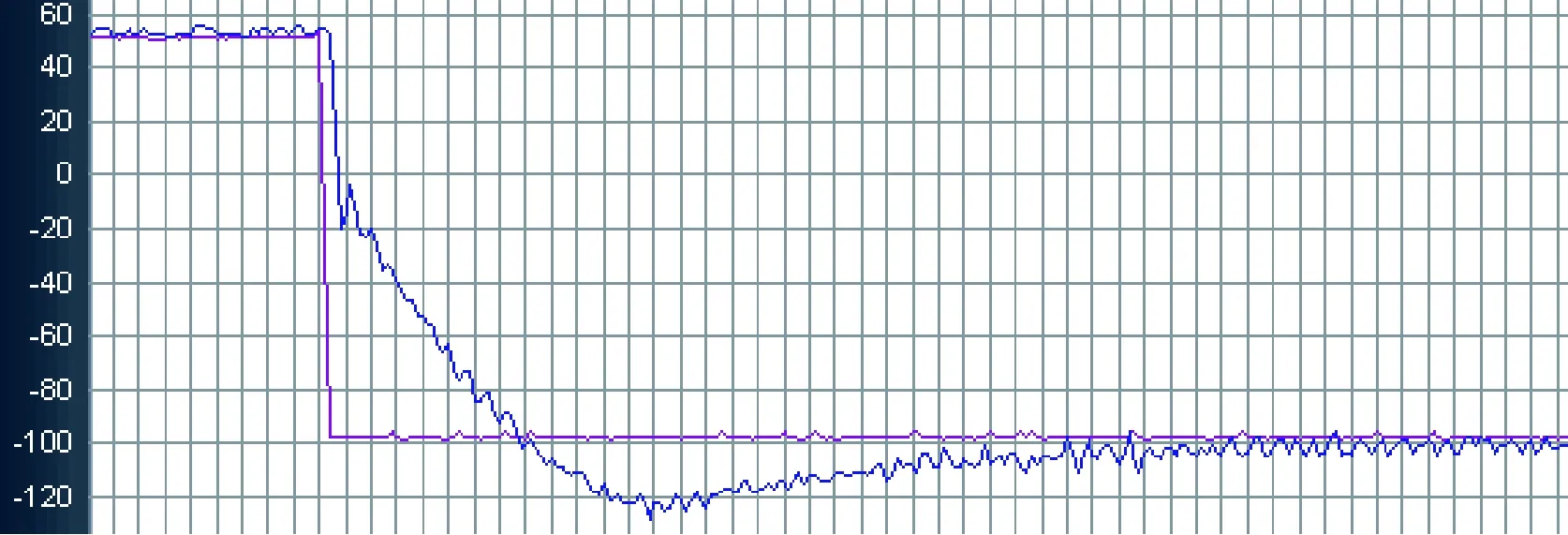
图12 阶跃给定时PID控制实验结果反色图

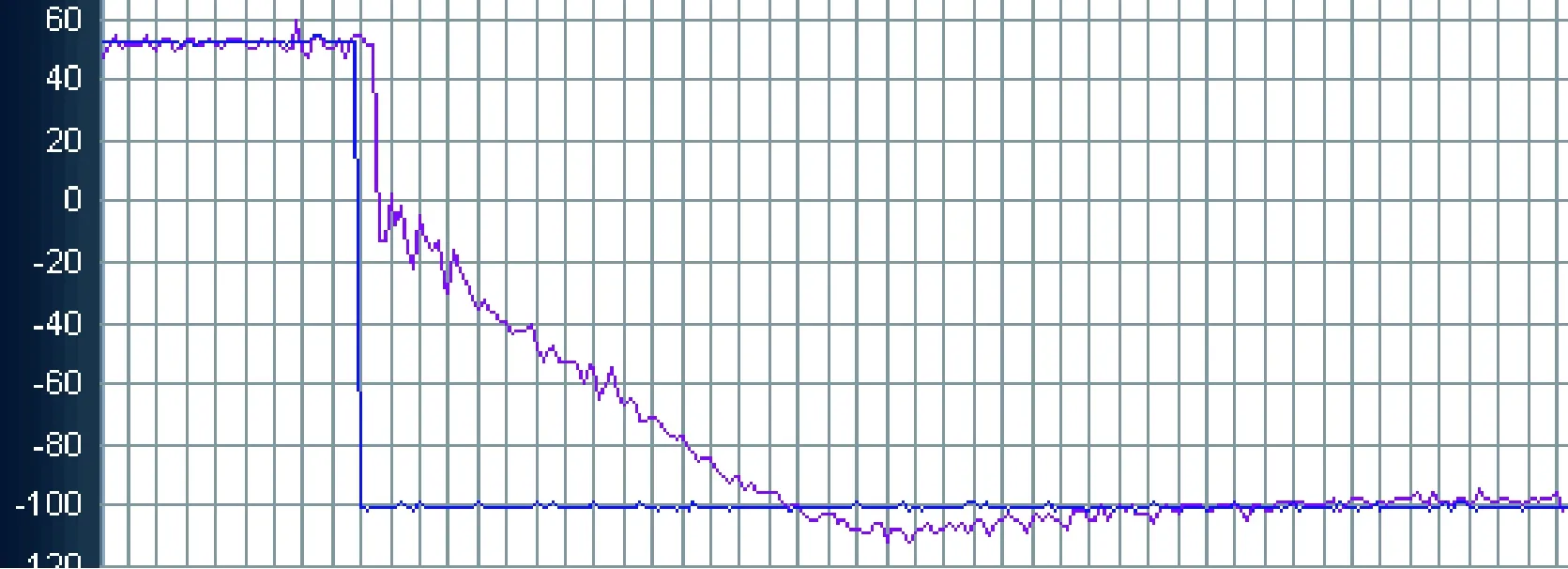
图13 阶跃给定时模糊PID控制实验结果反色图

定量分析图12、13，横坐标代表时间(每格50 ms)，纵坐标代表角度(每格20°)。实验结果表明，进行阶跃给定时，图12应用PID控制系统超调量较大，大概24°(1.2格)；峰值时间0.65 s(13格)。图13应用模糊PID控制，减小了超调量，10°以内(0.5格)；延长了峰值时间0.95 s(19格)。说明模糊PID控制在加强了稳定性能的同时牺牲了动态性能。

4 结 语

实验结果表明，DSP嵌入式控制器完全能够进行数字随动系统的控制，不仅是传统的PID控制，模糊PID控制算法在微控制器上也能实现。基于遗传算法对模糊控制输出量及对应比例因子的计算在控制效果上是可行的，能够大大缩短比例因子的整定时间。模糊PID控制相比较PID控制在稳定性上有所加强，在快速性上有所减弱。如何加强模糊PID控制在随动系统正反控制方向上的一致性有待进一步研究。

[1] 赵文龙，刘 洋，黄雅娜. 小功率随动系统中模拟校正装置的数字化设计与实现[J]. 实验技术与管理, 2013, 30(9): 58-62，71.

[2] 赵文龙，熊克勤，黄雅娜. 数字随动系统中嵌入式微控制器的设计[J]. 南昌航空大学学报(自然科学版), 2014(2): 97-104.

[3] 钱志良，章小红. 模糊控制在小功率位置随动系统中的应用[J]. 机电工程, 2006(8): 58-60.

[4] 燕 翔，张持健. 工业随动系统中模糊PID控制器的设计及应用[J]. 河北工业科技, 2011(3): 121-125.

[5] 孙前来. 模糊积分控制在位置随动系统中的应用[J]. 太原科技大学学报, 2009(3): 203-207.

[6] 韩 沛，朱战霞，马卫华. 基于模糊自适应PID的随动系统设计与仿真[J]. 计算机仿真, 2012(1): 138-142.

[7] Zhao Guoyong， Shen Yong， Wang Youlin. Fuzzy PID position control approach in computer numerical control machine tool[J]. Journal of Computers, 2013, 8(3): 622-629.

[8] Deng C，Xie S Q. Position error compensation of semi-closed loop servo system using support vector regression and fuzzy PID control[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(5-8): 887-898.

[9] 阳 睿，李英姿. 模糊PID控制的原子力显微镜仿真平台[J]. 实验室研究与探索, 2014, 33(1): 9-12，153.

[10] 李 娟. 自整定因子模糊PID控制器的设计与研究[D]. 镇江：江苏大学, 2007.

[11] 李国勇. 智能预测控制及其Matlab实现[M]. 2版. 北京: 电子工业出版社, 2010.

[12] 邓 可，贺向前. 基于遗传算法的自适应控制系统[J]. 实验室研究与探索, 2007, 26(10): 41-43，72.

[13] Ala Eldin Avdallan Awouda. New PID tuning rule using ITAE criteria[J]. International of Engineering, 2010, 3(6): 597-608.

[14] 殷 帅. ITAE在无刷直流电动机PID参数优化中的应用[J]. 微特电机, 2014, 42(9): 76-79.

[15] 姜长生，王从庆. 智能控制与应用[M]. 北京: 科学出版社, 2007.

Design of Digital Servo System Based on Genetic Fuzzy PID

ZHAOWenlong,HUANGXun

(College of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China)

According to the actual needs of course teaching of computer control technology, and the training of engineering students’ practical ability, a digital servo system was developed and TMS320F28335 was applied as controller. It applied genetic fuzzy PID compound control algorithm on MCU. The software of master computer was programmed based on MFC, it realized the serial communication of controller and PC. The data displayed on the PC with waveform that was more intuitive to analysis the control performance. The experimental results showed that there is a gap between actual control and Matlab simulation. Fuzzy control system had the better steady state but worse dynamic performance compared with PID control. The comparison between simulation and real system could make the students have a more intuitive understanding of the theory and practice, and could achieve good learning effect.

digital servo system； digital signal processor(DSP)； genetic algorithm; fuzzy-PID; compound control

2016-07-15

赵文龙(1963-)，男，江西上高人，硕士，教授，研究方向：嵌入式技术应用，计算机仿真与智能控制技术。

Tel.：13879136985；E-mail：1989121600@sina.com

TP 275

A

1006-7167(2017)03-0142-06