惯性式激振器研制及在模态测试中的应用

吴 帅， 胡科琪， 廖海黎， 李鋆胤

(西南交通大学 a.力学与工程学院; b.土木工程学院，成都 611730)

·仪器设备研制与开发·

惯性式激振器研制及在模态测试中的应用

吴 帅a， 胡科琪a， 廖海黎b， 李鋆胤a

(西南交通大学 a.力学与工程学院; b.土木工程学院，成都 611730)

以桥梁模态测试研究为工程背景，为解决桥梁模型模态测试中常规激振装置存在的不足，研制了一种小型惯性式激振器。该激振装置主要由步进电机、驱动器、控制器、齿轮传动部件、一对偏心质量块及底座组成。对某大跨度悬索桥模型进行激振，通过动力放大系数峰值处激振频率确定共振时模态频率，并与ANSYS有限元模型计算、锤击自由振动实验结果对比，证明了该激振器在桥梁模型模态测试中的适用性。该激振器具有质量轻、体积小、激振频率精准可控的特点，除在模型模态测试中的应用，还为实验教学及实际桥梁的激振提供了新的思路和方法。

模态测试； 惯性式激振器； 桥梁气动弹性模型

0 引 言

风洞试验作为考察结构空气动力特性的重要手段，在大跨度桥梁抗风设计中具有至关重要的作用[1-2]。在桥梁气动弹性模型风洞试验中，模型的振动模态测试是检验模型动力特性能否满足风洞试验要求的必要环节[3-4]。进行桥梁气动弹性模型模态测试的常用方法分为自由振动法和强迫振动法。自由振动法包括锤击法和人工激励法，通过采集模型的自由衰减振动信号来识别频率、阻尼等振动特征；强迫振动法则是采用激振器对模型施加激励，通过采集模型的稳态振动响应信号来识别振动模态参数。由于悬索桥、斜拉桥等大跨度桥梁气动弹性模型具有刚度小、质量轻、振动能量耗散快等特点，采用自由振动法进行模态测试往往难以获得准确的高阶模态参数。采用强迫振动法虽然能够激发出风洞试验所需的各阶模态，但由于激振器与模型之间连接，给模型提供了附加刚度或支撑，导致模态测试结果不准确[5]。

本文针对上述模态测试方法的不足，研制了一种小型惯性式激振器，用于桥梁气动弹性模型模态测试。通过对某大跨度悬索桥模型进行实验，验证了本文方法的有效性。

1 激振器工作原理与设计

1.1 激振器构成

本文提出的旋转偏心质量激振系统由机械作动器和控制部分组成。机械作动器主要由步进电机和机械部分组成，其中机械部分由变速齿轮、伞齿轮、传动轴与一对偏心质量块构成，如图1(a)所示；控制部分由CS20-1S串口控制器、ZD-2HD430步进电机驱动器和电源组成。本小型惯性式激振器结构框图见图1(b)。

(a) 机械作动器轴测图

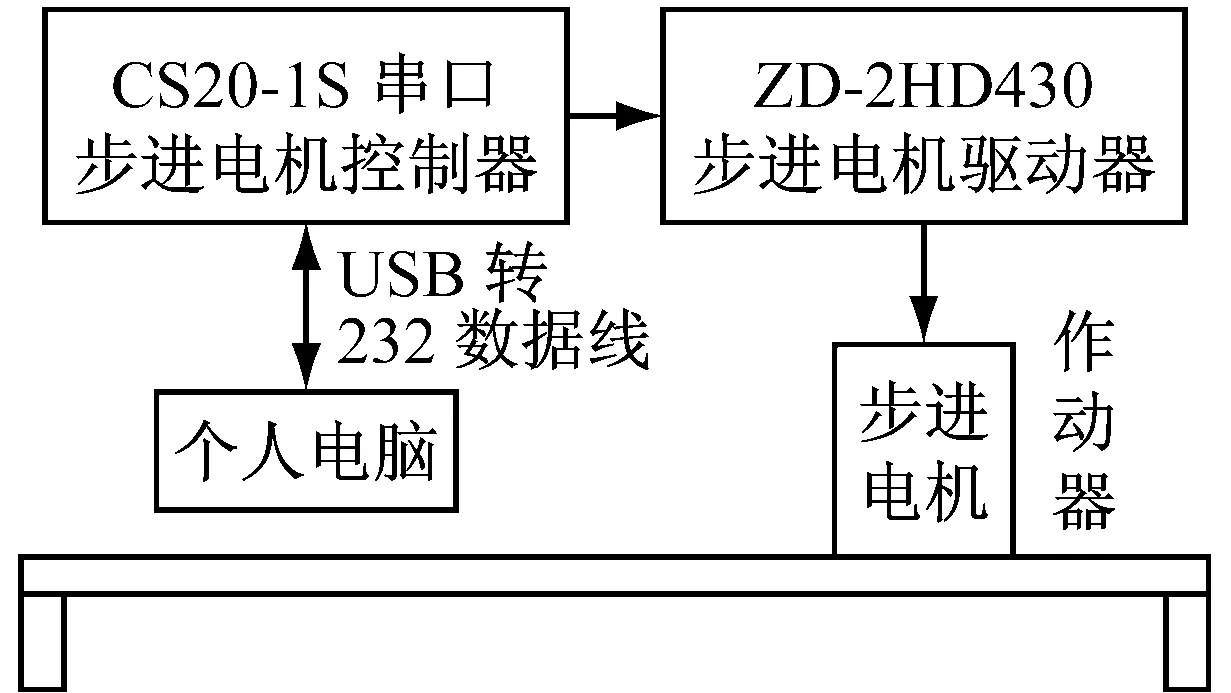
(b) 惯性式激振器系统构成

图1 小型惯性式激振器构成

1.2 激振频率控制

根据理论力学中动力学知识可知，旋转运动的转子将产生一个离心力[6]。设计的惯性式激振器，利用一对反向旋转偏心质量块，将水平方向惯性力相互抵消，最终合成得到一个垂直方向的正弦激振力,

(1)

式中：m为一个偏心质量块的质量；e为偏心距；ω0为质量块旋转频率。

使用CS20-1S步进电机控制器终端，设置步进电机控制器单位时间发出的脉冲信号数，经驱动器转化为强电流信号，驱动步进电机以固定频率转动。通过改变单位时间脉冲数改变电机转速，达到改变激振频率的目的。

根据振动测试中的要求，设计的激振器需要具有以下优点：①激振器机械作动部分质量与体积较小，可放置于激振对象上，并对其模态质量改变很小。②可以实现对激振频率的准确控制，且激振频率可以达到实验所需范围。

2 桥梁模型模态测试实验

针对某桥梁气弹模型，利用惯性式激振器设计模态测试实验，验证其在模型实验中的可行性。当激振器置于跨中单点激振时，桥梁主要产生对称竖弯变形，可将桥梁模型简化为单自由度的受迫振动模型，测量计算桥梁模型某阶模态频率，完成验证实验。

2.1 实验原理

根据结构动力学受迫振动基本原理[7-8]，简化后受简谐力作用的单自由度受迫振动位移幅值：

(2)

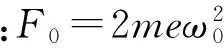
对于确定系统，位移幅值同时受F0、λ及ξ影响。电脑软件终端调整转子频率时，激振力幅值与频率比均改变。为找到振动幅值与频率比关系，令B0=F0/k，取动力放大系数

(3)

作动力放大系数与频率比和阻尼比关系图，得到系统的频率影响特性，如图2所示。

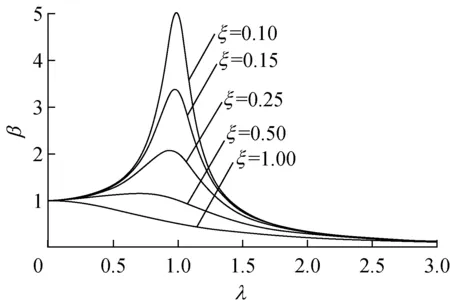
图2 系统频率响应曲线

由图2可见,在发生共振时，β达到峰值，ξ的变化对峰值出现时的λ影响很小。故可通过改变激振频率测量模型跨中振幅，计算对应的动力放大系数，当β达到峰值时，桥梁模型发生共振，由激振频率可获得桥梁模型某阶模态频率。

2.2 实验过程

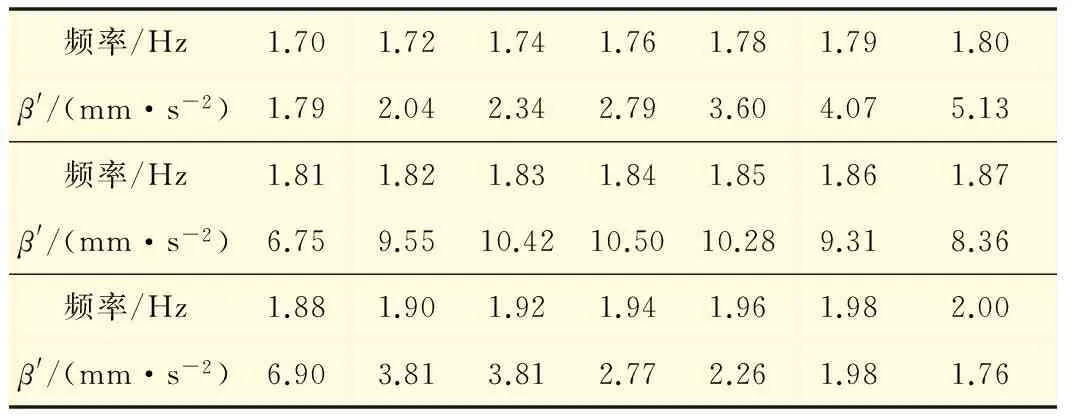
表1 频率-β′对应关系表

对表1中数据使用最小二乘法进行曲线拟合[9-11]，作频率与β′的关系曲线(见图3)。易得1.84 Hz时，β′达到峰值，此时β也位于最大值点，桥梁模型发生共振。则桥梁气弹模型一阶对称竖弯频率测量值为1.84 Hz。

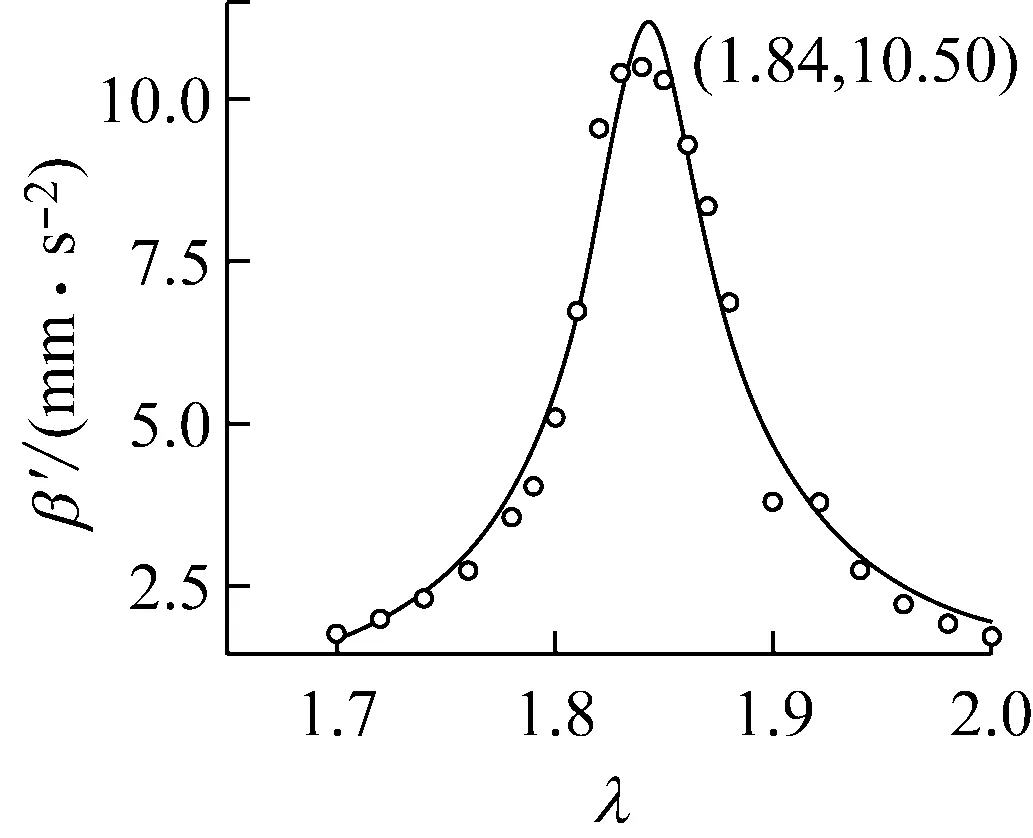
图3β′-λ关系拟合曲线

3 结果分析

3.1 振动模态有限元计算

本实验有限元模型数值计算利用大型通用有限元分析软件ANSYS。

由于实桥采用的是桁架型主梁断面，因此可以利用鱼刺梁式的单主梁方式，利用空间梁单元来模拟整个加劲梁，然后用刚臂与吊杆相连。主缆及吊索采用空间杆单元。索塔各构件均采用空间梁单元，对于变截面的中塔柱和下塔柱加密单元划分，且采用单元中央截面的几何特性。在计算过程中，不考虑支座的弹性和位移。

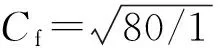
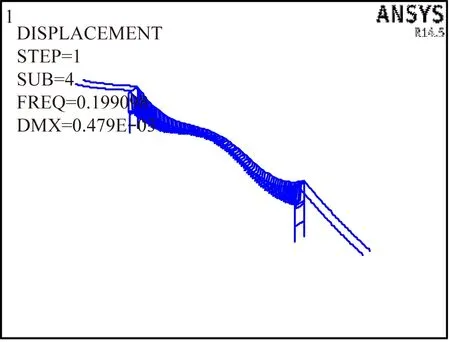
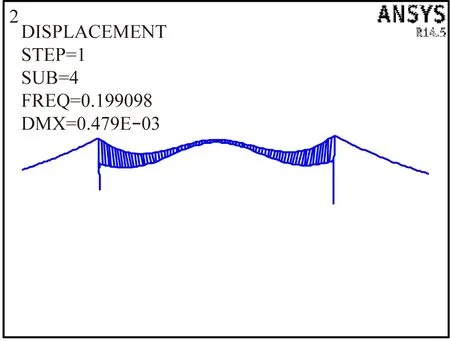
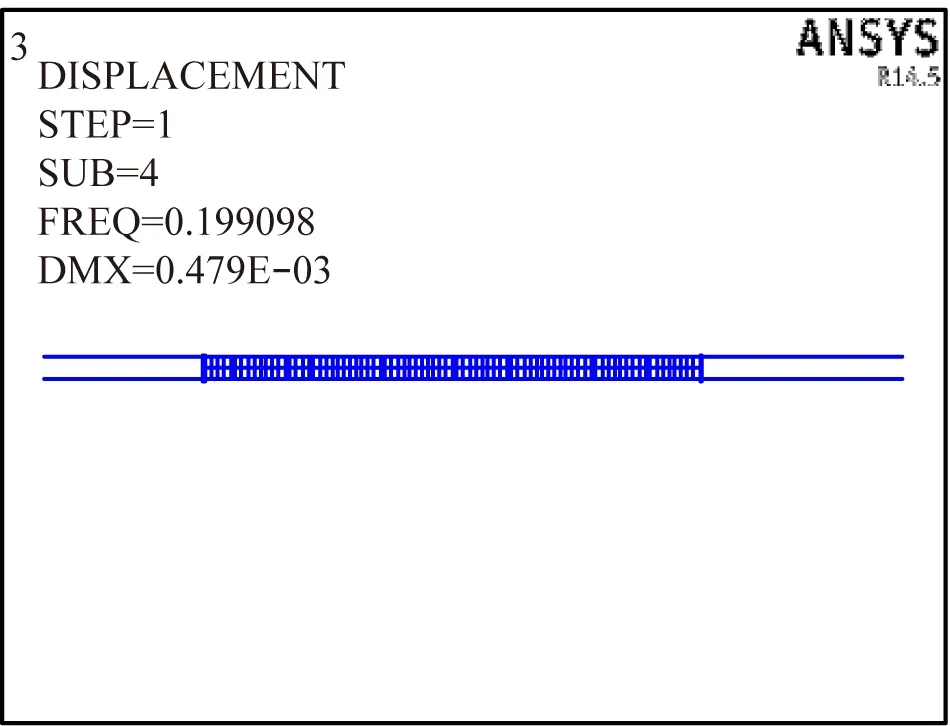
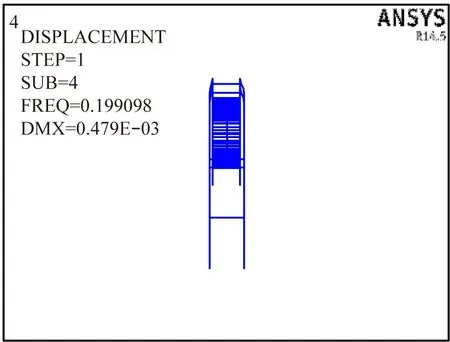
图4 一阶对称竖弯频率有限元计算值

通过激振器测量一阶对称竖弯模态频率的值1.84 Hz，较有限元理论计算值偏大。由于实桥建模获得的模态参数经频率比换算的到的1.78 Hz为气弹模型的设计期望值，与激振器测得1.84 Hz有3.26%的相对误差，表明模型存在一定设计误差，但仍在工程允许误差范围5%以内。

3.2 振动模态自由振动法测试

根据结构动力学，在确定与频率相关的参数时，频域分析方法是一种很高效的方法。频域分析技术就是将一些时域信号视为许多简谐信号的合成，利用频域分析将时域信号转化到频域上，从而进行数据的分析[13-14]。

桥梁模型自由振动时，振幅在系统阻尼作用下衰减，振幅与时间关系曲线如图5所示。利用Matlab编程，对激光位移传感器测得时间幅值信号做快速傅里叶变换，绘制振幅与频率关系曲线图[15]，如图6所示，得到桥梁模型的一阶对称竖弯频率为1.82 Hz。

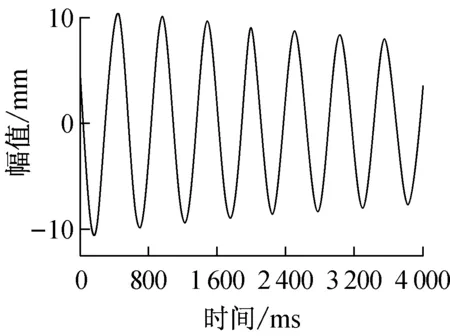
图5 自由振动时程

3.3 实验结果

将激振器激振测试结果及自由振动实验结果与有限元计算对比，计算相对误差，如表2所示。

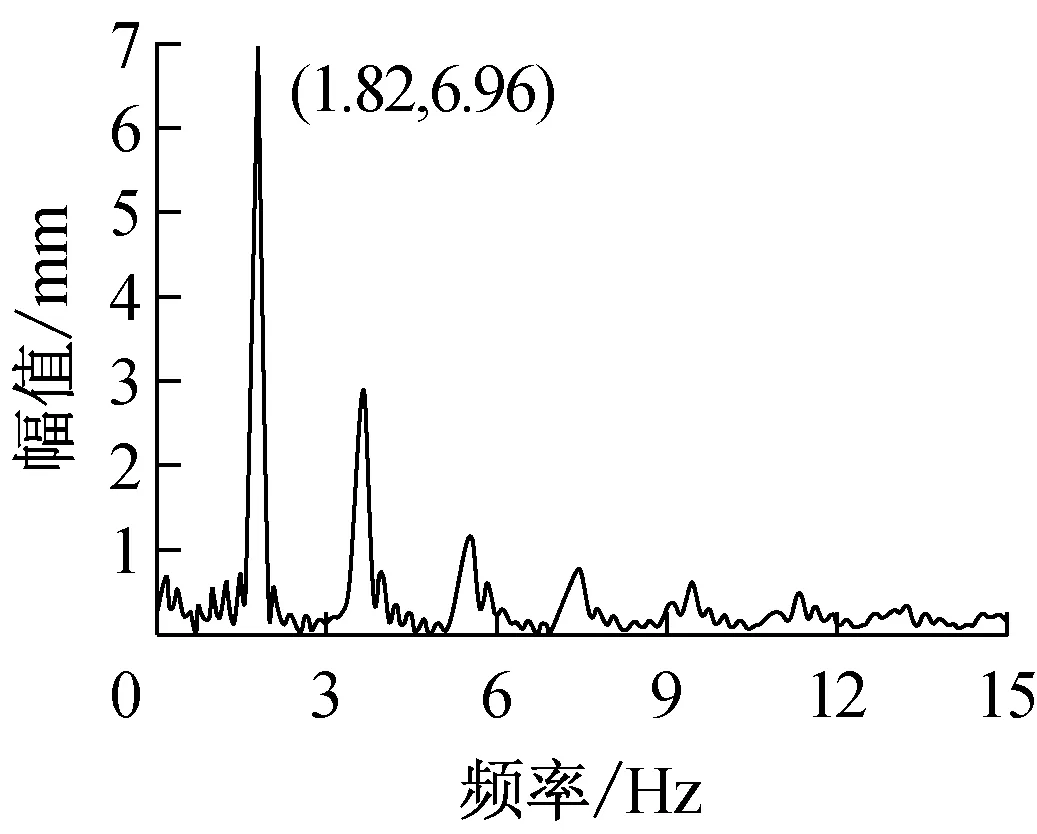
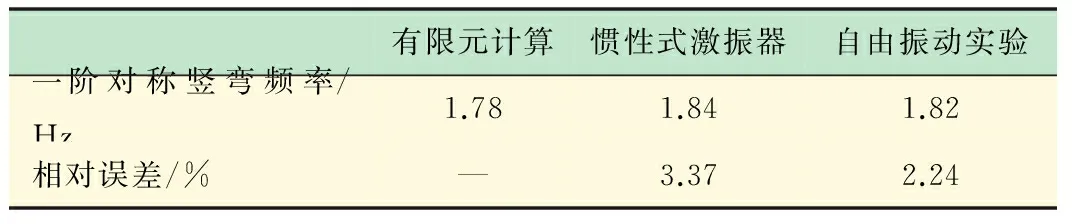
图6 自由振动幅频关系

显然，经过自由振动实验的验证，可知通过本小型惯性式激振器寻找共振频率的实验方法测得的一阶对称竖弯频率结果较为准确。与有限元计算结果存在3.37%的相对误差，说明桥梁气弹模型制作并未完全达到设计目标，但测量值与理论值相对误差仍在工程允许范围内(5%)。因此实验结果表明，此新型惯性式激振器有较高的可靠性、准确性，在振动测试实验中，有很好的可行性。

4 结 语

本文研制的惯性式激振器作为振动试验中的一种新型激励方式，控制精准、操作便捷，在大跨度桥梁气动弹性模型模态试验中具有显著优点，在振动测试实验教学中亦有应用前景。同时，利用本文设计原理可制造同类型大型激振器，为大跨度桥梁实桥模态测试提供一种新的激励手段。

本文采用研制的惯性式激振器仅对桥梁模型进行了一阶模态测试，旨在阐述其工作原理、实验方法及有效性。高阶模态测试的实验结果将另文介绍。

[1] 潘言全，冯大鹏. 国内桥梁的现状与应解决的问题[J]. 中国水运(学术版)，2007(8)：78-79.

[2] 《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2014[J]. 中国公路学报，2014(5)：1-96.

[3] 熊 龙，廖海黎，李明水,等. 马普托桥颤振稳定性的风洞试验研究[J]. 防灾减灾工程学报，2017(2)：1-6.

[4] 许福友，马如进，陈艾荣,等. 苏通大桥全桥气弹模型设计与模态调试[J]. 工程力学，2009(12)：150-154,174.

[5] 郭震山，宋锦忠，陈艾荣. 缆索承重桥梁全桥气动弹性模型模态测试分析[J]. 结构工程师，2003(4)：63-69.

[6] 黄安基. 理论力学[M].2版. 北京：高等教育出版社，2011：427-448.

[7] Clough W, Penzien J. Dynamics of Structures[M]. 2nd ed. New York：McGraw-Hill, 1995.

[8] 刘晶波，杜修力. 结构动力学[M]. 北京：机械工业出版社，2005：51-59.

[9] 侯超钧，曾艳姗，吴东庆. 全局连续的分段最小二乘曲线拟合方法[J]. 重庆师范大学学报(自然科学版)，2011(6)：44-48.

[10] 龚循强,李 通,陈西江. 总体最小二乘法在曲线拟合中的应用[J]. 地矿测绘，2012(3)：4-6.

[11] 李蓓蕾. 多次自适应最小二乘曲线拟合方法及其应用[D]. 荆州：长江大学，2014.

[12] 何 能. 桥梁气动弹性模型模态参数及颤振导数识别方法研究[D]. 成都：西南交通大学，2014.

[13] 王兆辉，樊可清. 用频域法识别桥梁的模态参数[J]. 五邑大学学报(自然科学版)，2005(3)：24-28.

[14] 单德山，李 乔. 桥梁结构模态参数的时频域识别[J]. 桥梁建设，2015(2)：26-31.

[15] 楚 涓，施 意，李诠娜. 基于Matlab的快速傅里叶变换的设计探讨[J]. 数字技术与应用，2015(10)：125-126.

Development of Small-scale Inertial Vibration Exciter and Application in Modal Test

WUShuaia,HUKeqia,LIAOHailib,LIJunyina

(a. School of Mechanics and Engineering; b. School of Civil Engineering, Southwest Jiaotong University, Chengdu 611730, China)

This paper presents the design, structure and test results of a new small-scale inertial vibration exciter. Under the engineering background of the modal tests of bridges, this paper describes the development of the exciter to solve some deficiencies of ordinary exciters. The device is made of stepping motor, motor driver, motor controller, gear set, counter-rotating dual-rotor and base. According to the modal test of a long-span suspension bridge model, the resonance modal frequency is determined by the frequency in which the dynamic magnification factor is maximum, and the test results of the inertial vibration exciter are compared with those of numerical calculation of ANSYS and hammering tests. It proves that this new small-scale inertial vibration exciter is applicative to the modal tests of bridge models. With the advantages of lightness, small volume and precisely controllable frequency of force, this exciter not only is applicative in modal tests of bridge models but also provides new idea and method for experiments teaching as well as excitation of real bridges.

model test; inertial vibration exciter; aeroelastic model of bridges

2016-07-21

国家自然科学基金资助项目(51378442);国家级大学生创新创业训练计划基金项目(201510613057)

吴 帅(1994-)，男，山西阳泉人，本科生。

Tel.:15680841225; E-mail: 123657502@qq.com

廖海黎(1956-)，男，四川资中人，教授，博士生导师，主要研究方向为桥梁风工程、结构风工程、振动控制。

Tel.: 028-87634825; E-mail: hlliao@home.swjtu.edu.cn

U 446.1

A

1006-7167(2017)03-0044-04