基于自优化的多属性高斯核函数相关向量机方法*

许玉格 刘莉 罗飞

(华南理工大学 自动化科学与工程学院, 广东 广州 510640)

基于自优化的多属性高斯核函数相关向量机方法*

许玉格 刘莉 罗飞

(华南理工大学 自动化科学与工程学院, 广东 广州 510640)

在相关向量机的预测模型中,核函数的选择和核参数的取值对模型预测性能影响很大.针对这一问题,文中采用多属性高斯核函数建立相关向量机预测模型,提出了一种自优化的核参数学习方法进行参数优化,并将该模型用于二维标准函数预测和污水处理系统出水水质预测,与不同核函数下的相关向量机模型以及不同参数优化方法下获得的预测模型进行了对比实验.结果表明,基于自优化的多属性高斯核相关向量机模型对低维数据的参数敏感度较低,对高维数据有良好的输出精度和稀疏性,在污水出水水质预测中获得比较满意的结果.

相关向量机;多属性;高斯核函数;自优化方法;污水处理

软测量和模型预测可将不易实际测量或测量成本过高的变量作为主变量,选取相关辅助变量,通过构造变量间的映射关系实现对主变量的估计和预测,作为一种经济、可靠和快速的测量方法,它已被广泛应用到各个工业领域[1-3].

人工神经网络、支持向量机和相关向量机是常用的软测量和模型预测学习方法,并取得了一定的成果[4-8].但神经网络存在局部极小、泛化能力有限等缺陷,使其在应用中受到约束.支持向量机的核函数选择受限于Mercer条件,对惩罚参数过于敏感[9].相关向量机(RVM)是基于统计理论贝叶斯框架下的稀疏性学习方法,属于监督机器学习算法,具有解更稀疏、核函数选择自由、泛化能力强、鲁棒性好等优点[10],但RVM模型的输出结果受核函数的影响,核函数的选择和核参数的确定影响相关向量机模型的预测性能,因此,为相关向量机选择合适的核函数并进行核函数参数优化,对相关向量机的性能至关重要.

在相关向量机的核函数中,高斯核函数最为常见[7-8].单一高斯核函数缺乏灵活性,对复杂映射关系的描述能力有限.对此,不少学者将由多个函数构成的核函数应用于相关向量机.组合核函数、多样本的高斯核函数(MSG)、多属性高斯核函数(MAG)均属于多核函数,文献[11-12]将基本核函数进行加权组合,模型在一定程度上比单核好,但该组合核函数对初始参数比较敏感[14].文献[13-14]使用多样本高斯核,该核函数的性能优于单核,但核参数个数与训练样本数相等,并且随着训练样本的增多而增大,使模型学习变得困难.多属性高斯核[15]比较灵活,其在各个属性上使用不同的核参数,具有较好的学习能力和泛化能力,核参数个数也比较少.另外,核参数的取值对预测模型性能的影响很大,因此研究适合于多属性高斯核函数相关向量机的参数优化方法非常必要.

基于上述分析,文中采用多属性高斯核函数建立相关向量机预测模型,提出了一种自优化的核参数学习方法进行核参数优化,以降低参数敏感度,提高预测精度;将该模型应用于二维标准函数预测和污水处理系统出水水质预测,并与不同核函数下的相关向量机模型进行了对比实验,以验证文中提出的多属性高斯核函数的自优化参数优化方法的有效性.

1 基于自优化的多属性高斯核函数相关向量机建模

1.1 多属性高斯核函数

多属性高斯核的形式如下[15]:

(1)

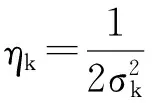
令φ(xn)=[1,k(xn,x1),k(xn,x2),…,k(xn,xN)]T,它为(N+1)×1维矩阵,N为样本个数,则MAG核构成的贝叶斯矩阵可表示为Φ=[φ(x1),φ(x2),…,φ(xN)]T,它是N×(N+1)维矩阵.1.2 多属性高斯核相关向量机建模原理

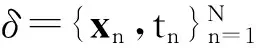
tn=y(xn,w)+εn

(2)

式中：w=[w0,w1,…,wN]T,是模型的权值向量；y(xn,w)可由核函数的加权模型表示,

(3)

若tn服从独立分布,则数据集的似然估计概率为

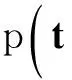
(4)

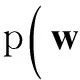
(5)

根据先验概率分布和似然估计分布,可得权重的后验概率分布:

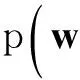
(6)

其后验均值u和协方差矩阵Σ分别为

u=β-1ΣΦTt

(7)

Σ=(β-1ΦTΦ+A)-1

(8)

(9)

式中,C=(σ2I+ΦA-1ΦT)-1.

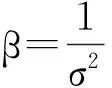
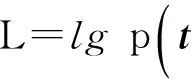
(10)

通过期望最大化算法(EM)迭代估计,获得使每代对数似然函数最大化的超参数更新公式:

(11)

其中，γi=1-αiΣii,Σii为Σ的第i个对角元素.

1.3 多属性高斯核参数自优化学习

参数的取值会影响模型性能,为了获得良好的模型性能,需要对模型参数进行学习,选取最优参数[16].

多属性高斯核函数中有d个核参数需要学习.由函数定义可知,核参数ηk的取值必须大于0,由于训练样本的多样性和不确定性,若不对参数学习过程中可能出现的ηk为0或负值情况加以处理,将导致核参数的学习失败.另外,在对核参数寻优的实验中发现:在单一高斯核函数的参数学习中,似然函数的更新呈现单调性,使得优化过程单调地快速收敛于最优值;在多高斯核函数的参数优化过程中,似然函数不一定呈现单调递增.针对以上问题,文中推导出一套多属性高斯核参数的自优化学习方法,将d个核参数转换成核参数几何平均值h,并引入参数ρ,保证在学习过程中核参数始终大于0,而且尽可能地使似然函数的更新呈现单调递增,保证核参数学习成功且最大似然估计值单调递增,最后收敛到最优值.具体参数更新过程如下.

设核参数几何平均值为h,使得

(12)

似然函数可写成如下带有拉格朗日因子的函数形式:

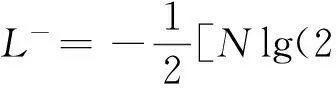
(13)

该模型对核参数求导,得

(14)

(15)

否则,为保证核参数均大于0且最大似然估计尽可能的大,梯度小于0的核参数更新公式为

ηi,new=ρηi

(16)

梯度大于0的核参数更新公式为

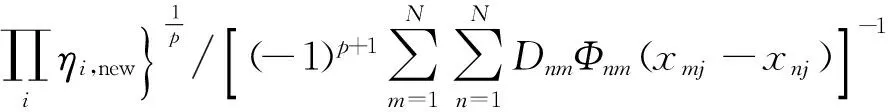
(17)

式中，i、j分别表示梯度小于0和梯度大于0的属性列,p为梯度大于0的属性列个数.

为保证模型收敛,当且仅当核参数的变化趋向于使最大似然估计值变大,则按式(15)-(17)更新参数,否则不更新核参数值.

1.4 多属性高斯核相关向量机建模步骤

基于自优化的多属性高斯核相关向量机建模步骤如下:

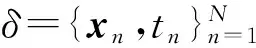
(2)初始化模型参数α=[N-2,N-2,…,N-2]T,σ2=0.1var(t),var(·)为方差函数,η=[h-2,h-2,…,h-2]T.

(3)按式(7)、(8)更新u和Σ.

(4)按式(11)更新超参数α和β.

(5)如果超参数αi大于给定的某个极大值(文中取e9),则认为该超参数趋于无穷,从而将相应的权值设为0,并且忽略相应的贝叶斯矩阵;否则,定义该训练样本为相关向量.

(6)如果最大似然估计值变大,则按式(15)-(17)更新核参数,并更新贝叶斯矩阵Φ,否则不对核参数和贝叶斯矩阵Φ进行更新.

(7)如果连续两代间的超参数α的最大变化值小于某一极小值(文中取e-3),则转步骤(8),否则转步骤(3).

(8)输出模型权值w、核参数η、相关向量个数Nr、噪声方差σ2.

2 仿真实验和结果分析

分别采用相关向量机性能测试中二维标准函数和污水处理过程的出水水质预测对6种相关向量机(单个高斯核函数的相关向量机(RVM)[15]、多样本高斯核函数相关向量机(MSG-RVM)[16]、组合核函数的相关向量机(C-RVM)[8,12]、基于遗传的多属性高斯核相关向量机(MAGE-RVM)[17]、基于梯度的多属性高斯核相关向量机(MAGD-RVM)[15]、自优化的多属性高斯核相关向量机(MAGO-RVM))进行仿真实验.实验参数设置如下:

1)RVM算法只有一个高斯核函数,采用遗传算法计算核参数的初始值.

2)MSG-RVM算法采用多样本高斯核函数,采用梯度下降法计算核参数,用遗传算法确定核参数的初始值.

3)C-RVM算法中核函数是由加权组合核函数k=akpoly+(1-a)kgauss构成,加权系数为a,多项式函数设为4阶.采用遗传算法获取初始核参数和加权系数a.

4)MAGE-RVM算法采用多属性高斯核函数,采用遗传算法来学习全部d个核参数(η1,η2,…,ηd).

5)MAGD-RVM算法使用多属性高斯核函数,利用梯度下降法计算核参数,用遗传算法确定初始核参数几何平均值h的取值.

6)MAGO-RVM算法采用多属性高斯核函数,采用文中提出的自优化来计算核参数,用遗传算法确定初始核参数几何平均值h和ρ.

将遗传算法的个体规模设为100,遗传代数分别设为20、50、100,6种模型中h和(η1,η2,…,ηd)的取值范围为[0,100],α和ρ的取值范围为[0,1].将目标值和预测值进行归一化,以均方根误差(RMSE)为目标函数.目标函数均方根误差公式为

(18)

相对均方根误差为

(19)

式中,yn是预测值,Nt是测试样本数.

2.1 二维标准函数实验

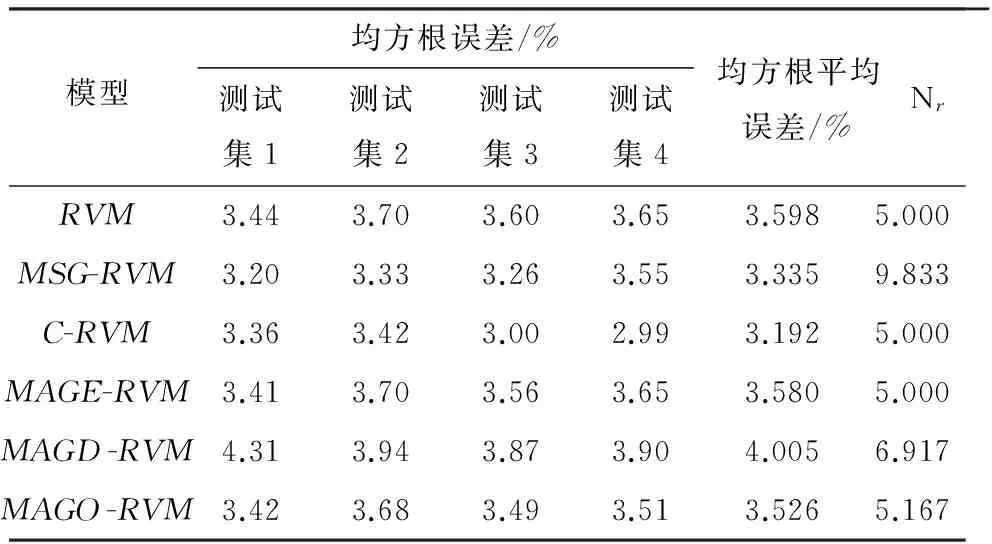
表1 6种模型的预测性能比较

从表1可知,6种模型的平均输出精度和稀疏性非常接近,多属性高斯核函数在低维数据下的性能没有太大优势.

文中从建模成功率和初始核参数的有效范围两方面分析6种模型对参数的敏感性.参数的敏感度可以理解为:在相同个体规模下使得建模失败的无效个体占总个体数的平均百分比,敏感度数值越高表示模型对参数的敏感性越大,建模成功率越低;模型取得良好预测效果的初始核参数范围越大,模型对参数的敏感度越低.6种模型对初始参数敏感度的对比结果如表2所示.从表中可知,基于多属性高斯核函数的相关向量机对初始参数的敏感度较低,受初始核参数值的影响较小.

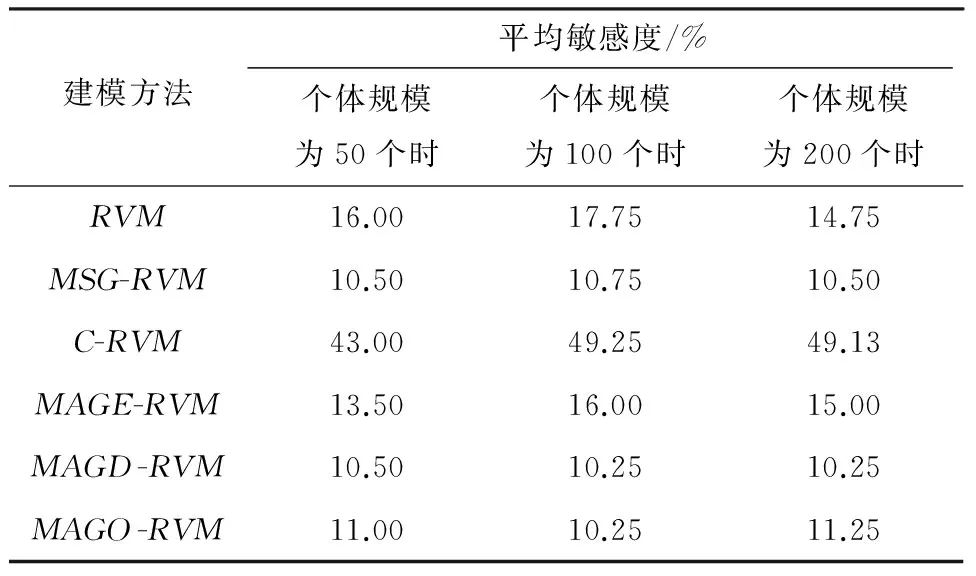
表2 6种模型的平均敏感度

在利用穷举法确定初始核参数的情况下进行实验,发现RVM的初始核参数在[1,8]内时预测效果较好,C-RVM合适的初始核参数范围为[2,10],MSG-RVM的初始核参数在[1,4]内时预测效果较好,MAGE-RVM模型的初始核参数为[1,8]、MAGD-RVM的初始核参数为[1,10]、MAGO-RVM的初始核参数为[0.01,20.00]时预测效果均较好.MAGO-RVM的初始核参数取值范围比其他模型更广.RVM和MAGO-RVM在初始核参数取不同值时的输出结果如图1所示.由图可见,RVM在初始核参数为0.01、20.00时均无法获得满意的输出效果,而MAGO-RVM在初始核参数为0.01、20.00时均可以保证输出效果良好.

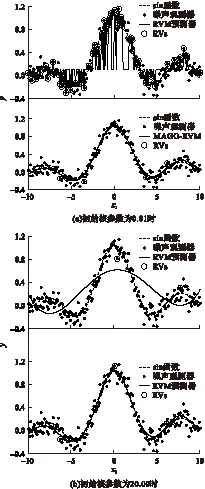
图1 RVM和MAGO-RVM在初始核参数取不同值时的输出结果比较

Fig.1 Comparison of output results between RVM and MAGO-RVM with different initial nuclear parameters values

2.2 污水处理系统的仿真实验

污水的主要污染来自于有机物,而有机物在水中因为好氧微生物的存在而处于不断变化中,很难运用定量来分析.因此在水质检测中,利用生物需氧量BOD、化学需氧量COD等指标来衡量污水受污染的程度[13].BOD、COD与悬浮固体的质量浓度,进水的化学需氧量及生物需氧量、流量、pH值等变量密切相关.使用软测量方法来预测BOD、COD等出水参数,必须借助辅助变量.污水仿真实验采用加州大学数据库(UCI)提供的污水数据(共527组,38维),经数据预处理后得到400组20维的数据,其中包含两个输出属性BOD、COD,该实验数据属于高维数据.归一化后的输入数据作为模型输入,建模所需18个辅助变量如下:输入生物需氧量(DBO-E)、输入化学需氧量(DQO-E)、二级沉降器输入pH值(pH-D)、二级沉降器输入生物需氧量(DBO-D)、二级沉降器输入化学需氧量(DQO-D)、输入沉淀物(SS-D)、二级沉降器输入悬浮固体物(SED-D)、输出pH值(pH-S)、输出悬浮固体物(SS-S)、输出沉淀物(SED-S)、初沉池输入生物需氧量(RD-DBO-P)、初沉池输入悬浮固体物(RD-SS-P)、二沉池输入生物需氧量(RD-DBO-S)、二沉池输入化学需氧量(RD-DQO-S)、整个污水厂生物需氧量(RD-DBO-G)、整个污水厂化学需氧量(RD-DQO-G)、整个污水厂悬浮固体浓度(RD-SS-G)、整个污水厂可降解固体浓度(RD-SED-G).

实验时,取前200组数据作为训练数据,后200组作为测试数据,建立预测模型.除了前面6种预测模型之外,还增加了SVM预测模型进行对比分析.在BOD预测中,SVM惩罚参数C=17.869 6,g=0.082 97;MAGO-RVM的核参数几何平均值h=24.337 2,ρ=0.237 9.在COD预测中,SVM惩罚参数C=99.995 8,g=0.058 9,核参数几何平均值h=80.777 5,ρ=0.099 8.7种模型对污水处理参数的预测性能如表3所示,MAGO-RVM模型对BOD、COD的预测结果与实际结果的对比如图2所示.

从表3可知:MAGO-RVM的BOD预测误差最小,支持向量个数也较少;在COD预测中,SVM预测误差最小,但支持向量个数达到82个,MAGO-RVM预测误差相对较小,相关向量个数也较少.从图2可知,MAGO-RVM的BOD和COD污水出水预测曲线直观地反映了MAGO-RVM对污水出水实际值的拟合情况.

表3 不同模型对污水BOD和COD的预测性能

Table 3 Prediction performance of different models for BOD and COD

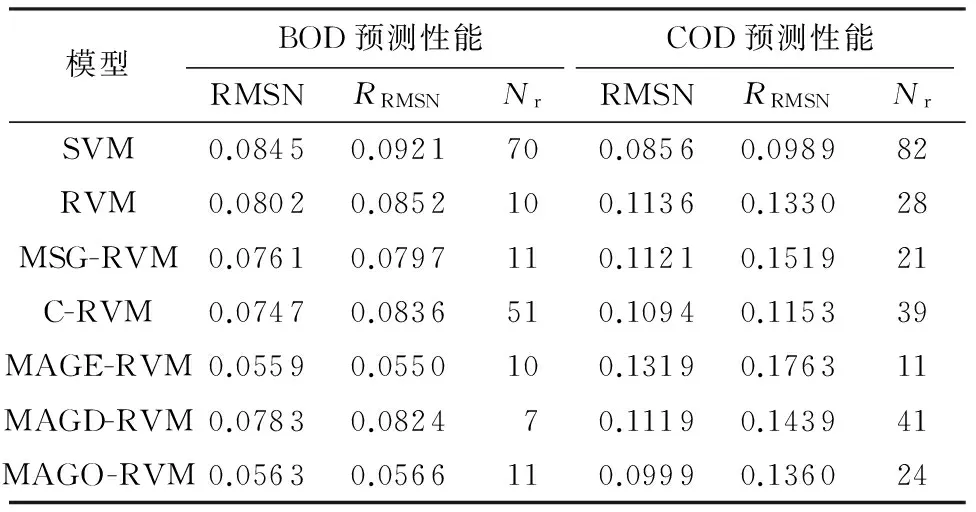
模型BOD预测性能COD预测性能RMSNRRMSNNrRMSNRRMSNNrSVM0.08450.0921700.08560.098982RVM0.08020.0852100.11360.133028MSG-RVM0.07610.0797110.11210.151921C-RVM0.07470.0836510.10940.115339MAGE-RVM0.05590.0550100.13190.176311MAGD-RVM0.07830.082470.11190.143941MAGO-RVM0.05630.0566110.09990.136024

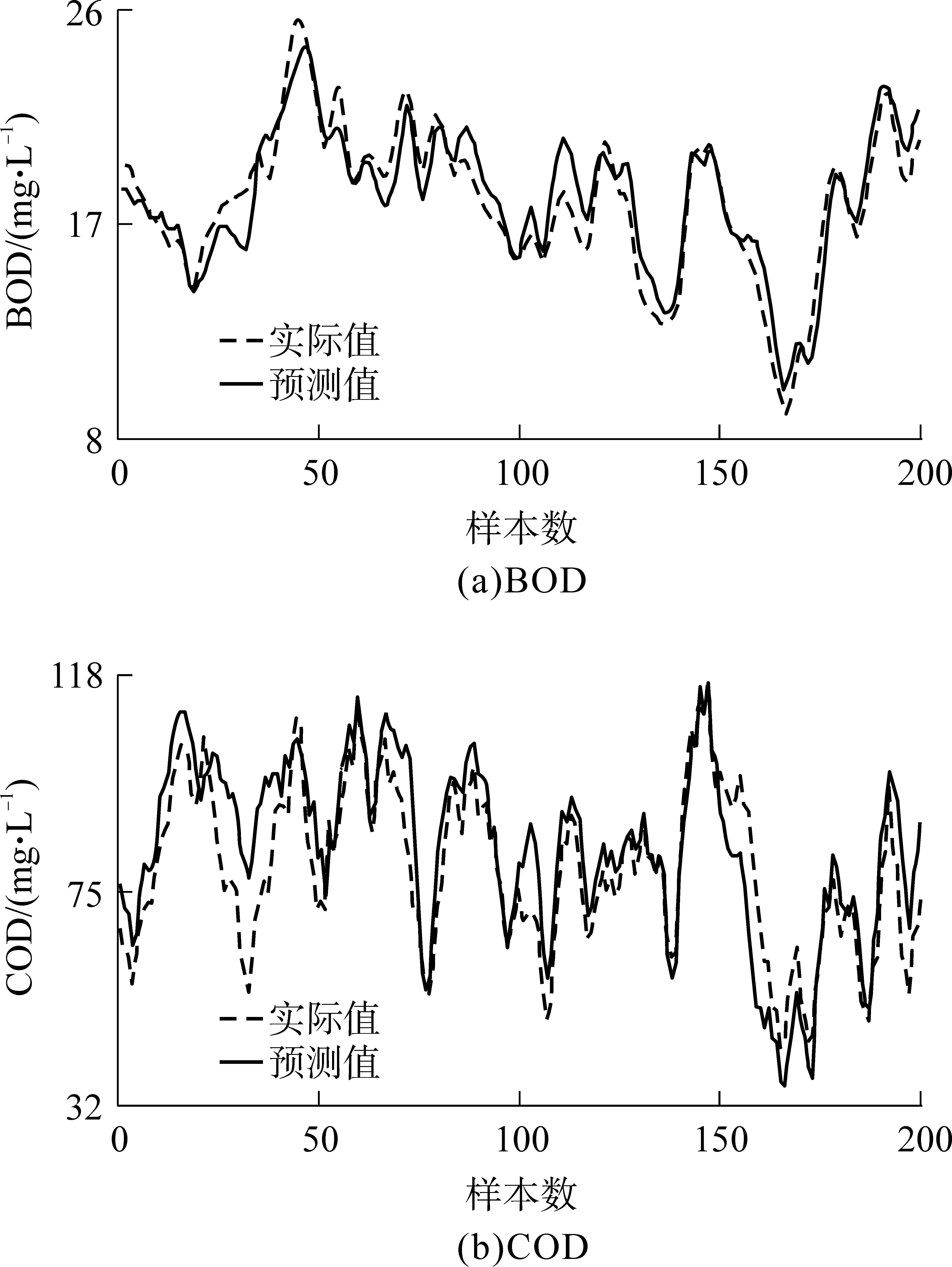
图2 MAGO-RVM模型对BOD和COD的预测值与实际值对比

Fig.2 Comparison of BOD and COD between the predictive values and the actual values by MAGO-RVM model

3 模型收敛性和稀疏性分析

采用自优化方法对核参数进行学习时,仅当核参数的变化趋向于使最大似然估计值变大时才对核参数进行更新,否则不改变核参数值,以保证模型在EM迭代估计过程中仍然满足最大似然估计函数单调递增的条件,从而使模型具有收敛性.

在污水的BOD仿真实验中,当模型取得最小均方误差而收敛时,6种模型收敛时的迭代次数见表4,RVM和MAGO-RVM模型的收敛曲线如图3所示,A为MAGO-RVM收敛点,B为RVM的收敛点.实验结果表明,相比于其他多核相关向量机,基于自优化的多属性高斯核相关向量机在收敛到最优值时需要的迭代次数最少,该结果验证了1.3节关于似然函数单调递增会加快收敛速度的分析.

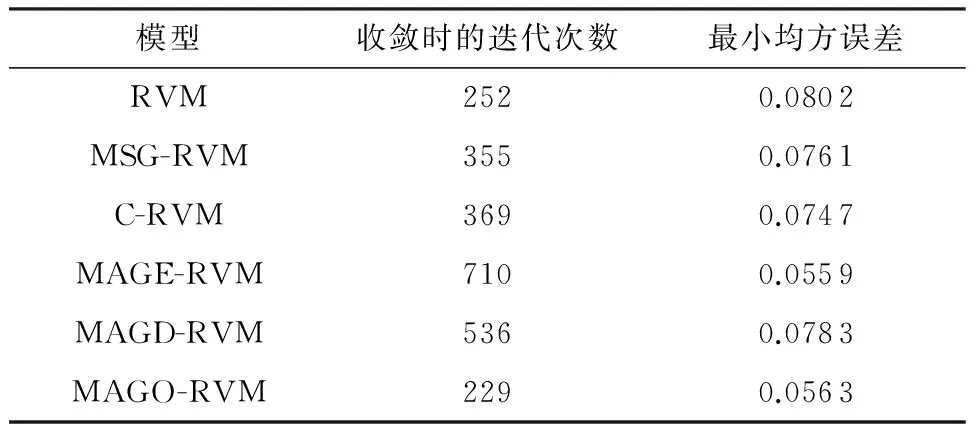
表4 6种模型的收敛性分析

图3 MAGO-RVM模型与RVM模型的收敛曲线

Fig.3 Convergence curves of MAGO-RVM model and RVM model

令RVM初始核参数和MAGO-RVM的核参数几何平均值相等,即两种模型的初始核参数取值相等.初始核参数取不同值时两种模型的均方根误差RMSE和相关向量个数如图4所示.从图中可知,文中提出的MAGO-RVM模型在提高预测精度的情况下并没有破坏模型的稀疏性.

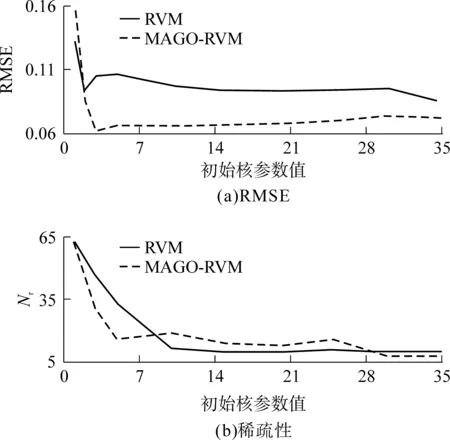
图4 MAGO-RVM模型与RVM模型的RMSE和稀疏性对比

Fig.4 Comparison of RMSE and sparsity between MAGO-RVM model and RVM model

由二维标准函数和污水处理的实验结果可知,基于自优化的多属性高斯核相关向量机模型对低维数据的参数敏感度较低,对高维数据在能够保证模型稀疏性和快速收敛性的同时获得较高的输出精度,获得了满意的污水出水水质预测结果.

4 结论

文中研究不同核函数下相关向量机的性能,针对多属性高斯核函数的相关向量机,提出了一种自优化的参数学习方法,在保证核参数学习成功的前提下尽快满足最大似然估计值单调递增,从而获得满意的核参数值.二维标准函数和污水出水水质预测实验结果表明,文中提出的模型能够获得比较满意的预测性能.文中提出的方法属于静态预测范畴,今后将在此基础上开展多属性高斯核函数相关向量机的在线软测量研究.

[1] MCCANDLESS T C,HAUPT S E,YOUNG G S.A regime-dependent artificial neural network technique for shor-trange solar irradiance forecasting [J].Renewable Energy,2016,89:351-359.

[2] CHEN Z M,HU J.Wastewater treatment prediction based on chaos-GA optimized LS-SVM [C]∥Proceedings of the 2011 Chinese Control and Decision Conference.Mianyang:IEEE,2011:4013-4016.

[3] ELARAB M,TICLAVILCA A M,TORRES-RUA A F,et al.Estimating chlorophyll with thermal and broadband multispectral high resolution imagery from an unmanned aerial system using relevance vector machines for precision agriculture [J].International Journal of Applied Earth Observation & Geoinformation,2015,43:32-42.

[4] CIVELEKOGLU G,YIGIT N O,DIAMADOPOULOS E. Modelling of COD removal in a biological wastewater treatment plant using adaptive neuro-fuzzy inference system and artificial neural network [J].Water Science and Technology,2009,60(6):1475-1487.[5] LI G H,ZHENG H.Application of artificial neural network in wastewater treatment [C]∥Proceedings of the 2nd International Conference on Information Science and Engineering.Hangzhou:IEEE,2010:4370-4372.

[6] YANG B L,ZHAO D A,ZHANG J.Prediction system of sewage outflow COD based on LS-SVM [C]∥Procee-dings of the 2nd International Conference on Intelligent Control and Information Processing.Harbin:IEEE,2011:399-402.

[7] KHADER A I,MCKEE M.Use of a relevance vector machine for groundwater quality monitoring network design under uncertainty [J].Environmental Modelling & Software,2014,57:115-126.

[8] 许玉格,曹涛,罗飞.基于相关向量机的污水处理出水水质预测模型 [J].华南理工大学学报(自然科学版),2014,42(5):103-108.

XU Yu-ge,CAO Tao,LUO Fei.The prediction of effluent quality of wastewater treatment based on relevancevector machine [J].Journal of South China University of Technology(Natural Science Edition),2014,42(5):103-108.

[9] 柳长源.相关向量机多分类算法的研究与应用 [D].哈尔滨:哈尔滨工程大学,2003.

[10] 杨树仁,沈洪远.基于相关向量机的机器学习算法研究与应用 [J].计算技术与自动化,2010,29(1):43-47. YANG Shu-ren,SHEN Hong-yuan.The research and application of machine learning based on relevance vector machine [J].Computing Technology and Automation,2010,29(1):43-47.

[11] WU B,ZHANG W Q,LIANG J H.A genetic multiple kernel relevance vector regression approach [C]∥Proceedings of the Second International Workshop on Education Technology and Computer Science.Wuhan:IEEE,2010:52-55.

[12] ZHAO L,SU Y D,QIN H.Study of multiple-kernel relevance vector machine based on kernel alignment [J].Applied Mechanics & Materials,2012,50(6):1308-1312.

[13] MOHSENZADEH Y,SHEIKHZADEH H.Gaussian kernel width optimization for sparse Bayesian learning [J].IEEE Transactions on Neural Networks & Learning Systems,2015,26(4):1-6.

[14] YUAN J,BO L,WANG K.Adaptive spherical Gaussian kernel in sparse Bayesian learning framework for nonli-near regression [J].Expert Systems with Applications,2009,36(2):3982-3989.

[15] TIPPING M E.Sparse Bayesian learning and the relevance vector [J].Journal of Machine Learning Research,2001,1(3):211-244.

[16] YUAN J,BO L F,WANG K S,et al.Adaptive spherical Gaussian kernel in sparse Bayesian learning of framework for nonlinear regression [J].Expert Systems with Applications,2009,36(2):3982-3989.

[17] 李刚,王贵龙.RVM 核参数的遗传算法优化方法 [J].控制工程,2010,17(3):123-126.

LI Gang,WANG Gui-long.Genetic algorithm optimization method of RVM kernel parameters [J].Control Engineering of China,2010,17(3):123-126.

A Self-Optimal Relevance Vector Machine with Multiple-Attribute Gaussian Kernel Functions

XUYu-geLIULiLUOFei

(School of Automation Science and Engineering, South China University of Technology, Guanzhou 510640, Guangdong, China)

In relevance vector machine prediction models, the selection of kernel functions and the values of kernel parameters have great influence on the prediction performance of the models. Aiming at this issue, a novel relevance vector machine prediction model is constructed on the basis of multiple-attribute Gaussian kernel functions, and a self-optimal kernel parameter-learning method is proposed to optimize the kernel parameters. Then, the constructed model is used to predict a two-dimensional standard function as well as the effluent quality of a wastewater treatment system. Finally, this model is compared with several models using different kernel functions and several models using different parameter optimization methods by simulation experiments. The results indicate that the proposed model is less sensitive to lower dimension data and has better output accuracy and sparsity in dealing with higher dimension data, and that it shows a satisfying performance in predicting the effluent quality of wastewater.

relevance vector machine; multiple attributes; Gaussian kernel function; self-optimization method; wastewater treatment

1000-565X(2017)01- 0088- 07

2015- 05- 27

广东省科技计划项目(2016A020221008,2016B090927007);广州市科技计划项目(201604010032)

Foundation items： Supported by the Science and Technology Planning Project of Guangdong Province(2016A020221008,2016B090927007)

许玉格(1978-),女,博士,副教授,主要从事数据挖掘和机器学习研究.E-mail:xuyuge@scut.edu.cn

TP 39

10.3969/j.issn.1000-565X.2017.01.013