一类耦合映射模糊时滞跟驰系统的反馈控制*

翟聪 刘伟铭† 谭飞刚,2

(1. 华南理工大学 土木交通学院, 广东 广州 510640; 2. 深圳信息职业技术学院 交通与环境学院, 广东 深圳 518172)

一类耦合映射模糊时滞跟驰系统的反馈控制*

翟聪1刘伟铭1†谭飞刚1,2

(1. 华南理工大学 土木交通学院, 广东 广州 510640; 2. 深圳信息职业技术学院 交通与环境学院, 广东 深圳 518172)

由于驾驶员在感应车间距变化时存在时变滞后的问题,且其灵敏度随着不同的车速和车间距在一定范围内波动,为了准确描述车辆在行驶过程中的运行状态,文中在耦合映射(CM)跟驰模型基础上,提出了一类模糊滞后CM跟驰模型,并对该模型的稳定性进行了分析.利用Lyapunov函数给出了模糊控制器存在的充分条件,使闭环跟驰系统满足稳定性,即交通拥挤现象能够得到有效抑制,并通过求解线性矩阵不等式(LMI)得到所设计的控制器.仿真实验表明,在该模糊控制器作用下,各辆车的速度震荡幅度得到了有效的降低,且能够更快地恢复到平稳状态,同时有效降低了车辆的二氧化碳排放量,说明该方法对于抑制交通拥挤和降低二氧化碳排放量是有效的.

耦合映射跟驰模型;模糊控制;滞后反应时间;稳定性;线性矩阵不等式

近年来,随着交通需求的日益增大,交通拥挤变得愈发严重.为了探讨交通拥堵产生的机理,有效地缓解交通拥挤问题,人们提出了很多交通流模型,如元胞自动机模型[1]、水动力模型[2]、跟驰模型[3]等.然而以往主要是利用微分方程对车辆跟驰行为进行分析,对于复杂的跟驰行为存在微分方程难以求解和可视化的情况.为了解决上述问题,Yukawa等[4-5]将耦合映射理论运用到交通建模中,使耦合映射(CM)跟驰模型得到了迅速的发展.Ge等[6]考虑了相邻前、后车车间距的影响,提出了一类新的CM跟驰模型,并设计了一类动态控制器;Han等[7]提出了一类驾驶员灵敏度非恒定的CM跟驰模型.深入的研究发现,驾驶员在驾驶过程中感知车辆信息的变化存在着一定的滞后时间.基于此,Zhao等[8]基于CM跟驰模型设计了新的含滞后项的反馈控制器,有效抑制了瓶颈路段上的交通拥挤状况;Fang等[9]在考虑连续车辆速度差对车流稳定性的影响后,设计了静态和动态的反馈控制器用于抑制交通拥挤现象;Zhang等[10]设计了一类新的滞后反馈控制器,该控制器能够有效降低交通过程中CO2的排放量.其余关于跟驰模型的研究可参考文献[11-14].

尽管已经有很多学者对CM跟驰模型进行了研究,但现有的CM跟驰模型存在以下的保守性:①假定驾驶员的滞后时间是恒定的,但Schultz[15]基于数据验证发现,驾驶员的滞后时间在一定范围内缓慢波动,故把驾驶员的滞后时间视为恒定过于理想化;②假设驾驶员的灵敏度是恒定的,但实际调查结果显示,驾驶员在不同车速和车间距下的灵敏度是不同的,一般情况下在拥挤道路上驾驶员的灵敏度要略高于在空旷的道路上.因此,为能准确描述车辆在行驶过程中的运行状态,文中在CM跟驰模型[16]的基础上引入时变滞后反应时间,提出了一类新模糊滞后CM跟驰模型,并对该模型的稳定性进行分析;基于分段Lyapunov函数给出了CM跟驰系统渐近稳定的充分条件以及模糊状态反馈控制器的设计步骤,并通过求解线性矩阵不等式(LMI)得到该控制器;最后通过仿真实验来验证该方法的有效性.

1 CM跟驰模型的描述

针对图1所示的单车道车辆跟驰行为,文中提出了一类CM模糊时滞跟驰系统(1).

图1 N辆车行驶在单车道示意图

Rj:如果vi且yi，则

(1)

(i=1,2,…,N)

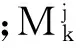
(2)

yi(k)=φ(k), k=-2,-2+1,…，1,0.

文中通过中心平均反模糊化和乘积推理得到系统全局模型如下:

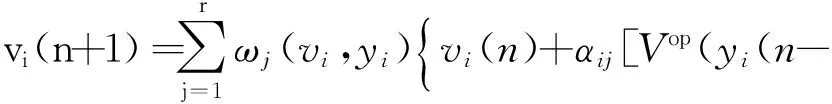
αij[Vop(yi(n-

(3)

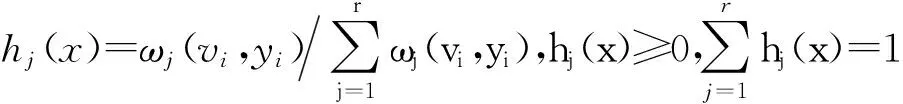
为了保持研究的一致性,文中仍然沿用分段线性OV函数[3]

(4)

式中:Hsat(·)为一类饱和函数,

vmax>0为车辆的最大行驶速度;η>0为车辆的安全间距;ζ为调节参数.

考虑头车以恒定速度v0匀速行驶,则模糊滞后跟驰系统(1)的稳定性状态为

(5)

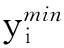
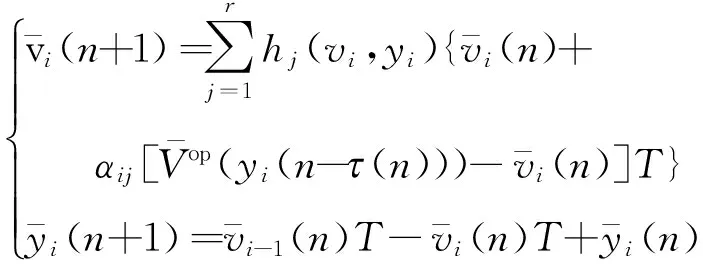
(6)

(i=1,2,…,N)

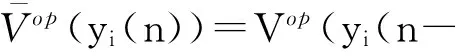
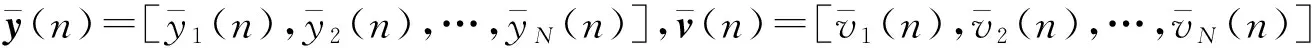
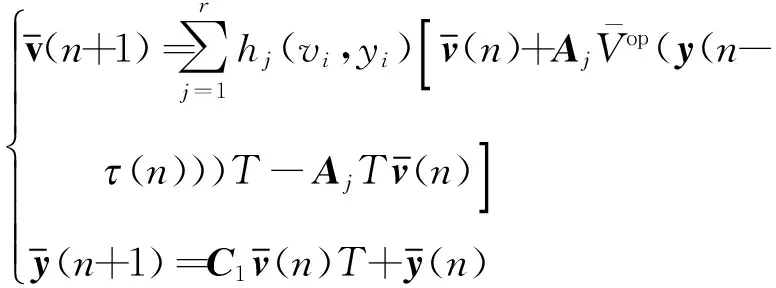
(7)

式中:Aj=diag{a1j,a2j,…,aNj},

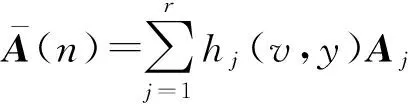
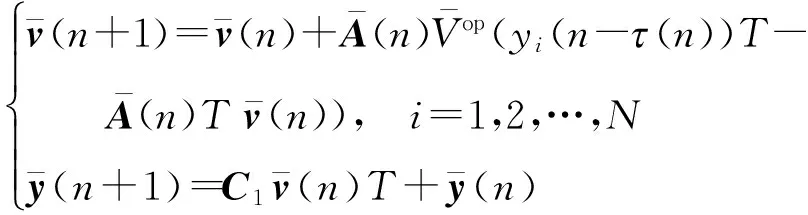
(8)

2 CM跟驰模型的稳定性分析

定理1 考虑CM跟驰模型(1),其中滞后反应时间(n)满足条件(2),对于任意的ε>0,如果存在正数γ、正定矩阵Pi(i=1,2)和Qj(j=1,2,3),使得下列线性矩阵不等式成立

(9)

则称CM跟驰模型(1)是稳定的,其中*表示的是对称矩阵.

证明 构造Lyapunov-Krasovskii泛函

V(n)=V1(n)+V2(n)+V3(n)

(10)

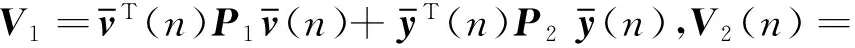
定义ΔV(n)=V(n+1)-V(n),则通过求解式(10)得到:

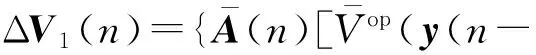
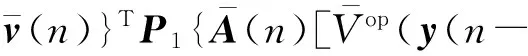
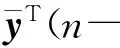
考虑非线性项(4),对于任意的标量ε≥0,可得

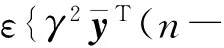
(11)

通过利用式(11)可得

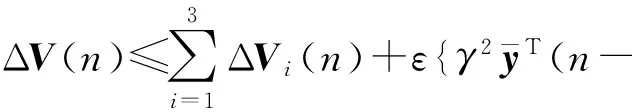
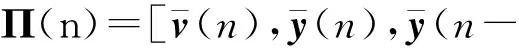
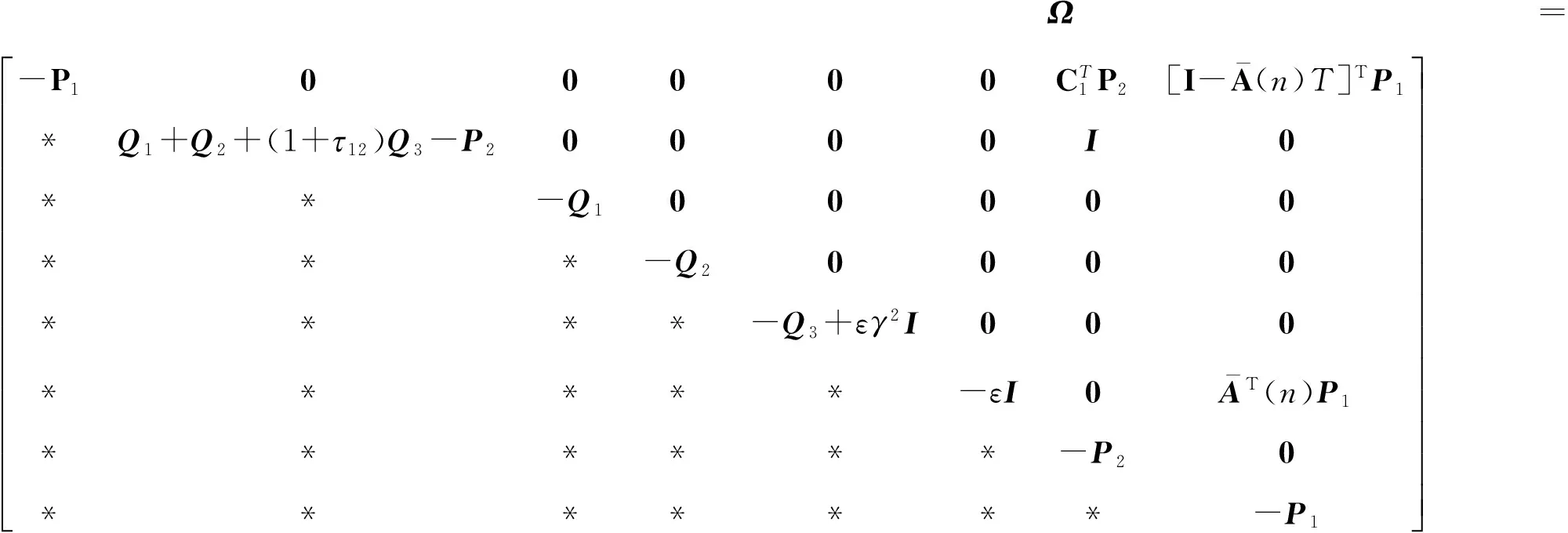
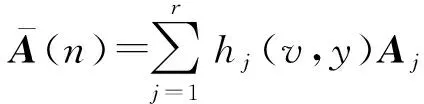
根据式(9)可知ΔV(n)≤0,即由稳定性理论可知跟驰系统(1)是稳定的.

3 模糊反馈控制器设计

交通拥堵必然会引起交通事故以及交通瓶颈,为了缓解交通拥堵,减小交通压力,文中通过考虑连续车辆速度差对车队稳定性的影响,引入并行分布补偿原理(PDC)对每个线性子系统都设计局部的反馈控制器,即Rl:如果vi且yi，则ui(n)=Kil(vi-1(n)-vi(n)). 则整个系统的控制律为各个子系统局部反馈控制的加权和,即

(12)

(13)

(i=1,2,…,N)

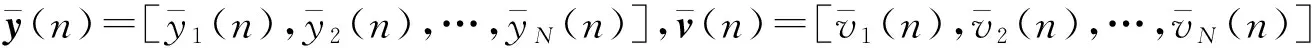
(14)

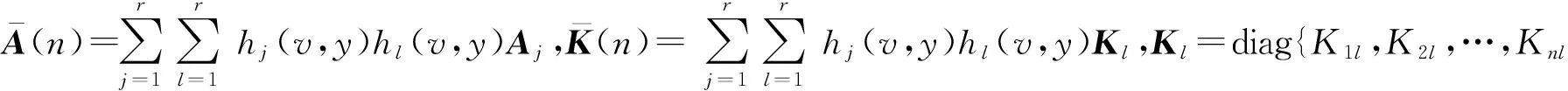
(15)

(16)

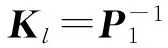
证明 构造形如式(10)的Lyapunov-Krasovskii泛函V(n)，定义ΔV(n)=V(n+1)-V(n),则通过求解得到

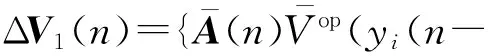
ΔV3(n)=).

基于非线性项(11)可得

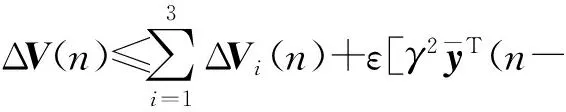
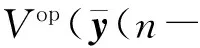
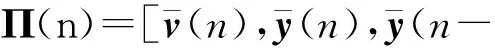
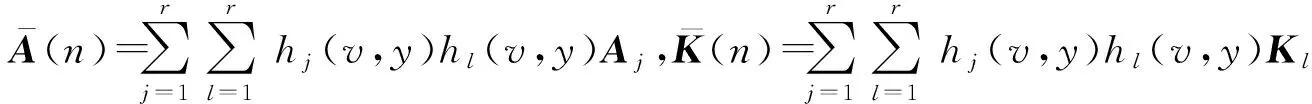
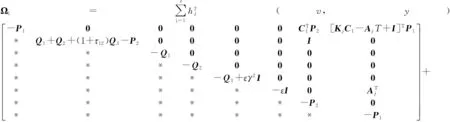
根据式(15)、(16)可知ΔV(n)≤0,即由稳定性理论可知闭环跟驰系统(14)是稳定的,即存在形如式(12)的状态反馈控制器,使得交通拥挤现象能够得到有效的抑制.

4 仿真实验

为了研究的一致性,文中仍然沿用文献[1]的参数,假设有11辆车行驶在开放边界的单车道上,且车与车之间不允许有超车行为,头车以v0=20 m/s匀速行驶,车辆的最大行驶速度为vmax=33.6 m/s,最短安全距离为ymin=7.02 m,中性安全距离η=25 m,调节系数ζ=23.3,采样时间为T=0.1 s.根据文献[12],驾驶员的滞后反应时间应该是在一定范围内缓慢波动的. 基于此,文中假设滞后时间函数为(n)=1+,满足(n)[1,2],1=0.6,2=1.4.

文中借助模拟驾驶生理仪对不同人在不同驾驶环境下的驾驶心理行为进行分析,结果发现,在车辆行驶速度较高且与前车间距较小时,驾驶员的灵敏度会高于正常情况;类似地,在车速较低且与前车间距较大时,驾驶员的灵敏度会低于正常情况.基于此,文中引入模糊控制理论,且为了研究方便,将驾驶员的灵敏度分为强、适中和弱3类,车辆的行驶速度和车间距分别分为慢、快、适中和近、远、适中3类,具体如图2所示.

当头车在第100秒至第120秒内受到外部扰动影响时,速度降为0,即当100 s≤nT≤102 s时,x0(n)=0.在无控制器作用下车辆的运行情况如图3所示.从图3(a)可知,在头车遭受外部干扰时,其余车辆的速度也相应发生变化,且各车变化幅度剧烈,震荡时间长;从图3(b)发现该震荡很明显地向后扰动传播;从图3(c)可知,车辆的车间距震幅很大,这间接说明了车辆在该时间内加、减速频繁,车辆的抗干扰能力差,收敛性不足,当存在外部干扰时,容易引发交通拥挤.

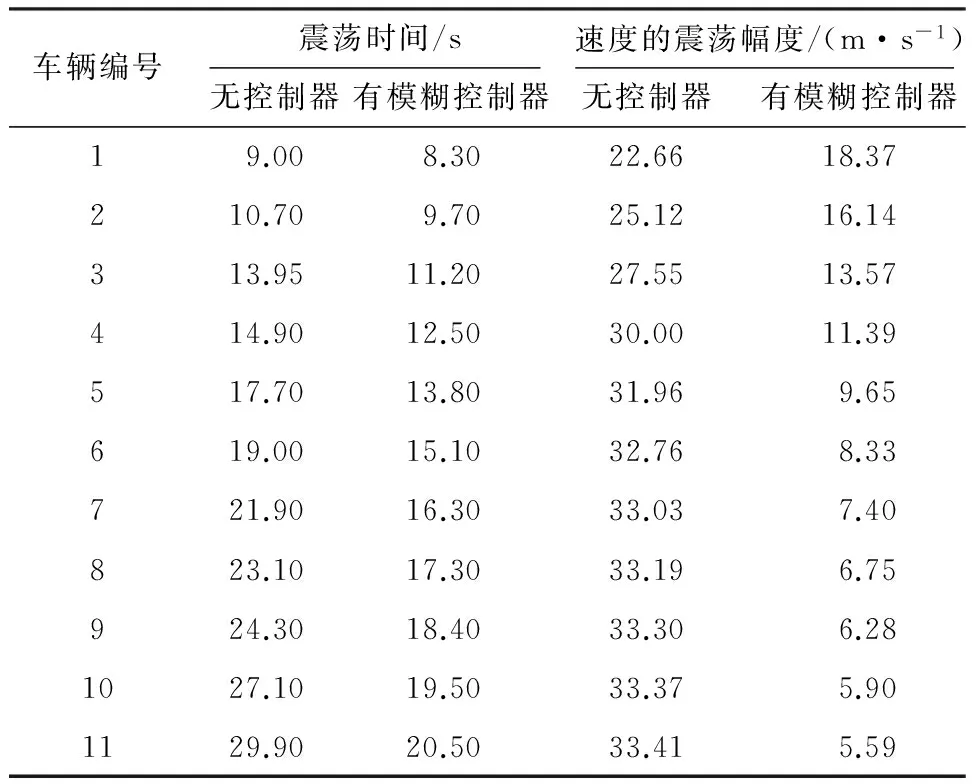
为了有效地缓解交通拥挤现象,提高车辆的抗干扰能力,文中利用Matlab的LMI工具箱对定理2进行求解,得到所设计的控制器参数为ki=0.6(i=1，2，…，11),在该控制器作用下车辆的运行情况如图4所示.从图4(a)可知,第1、6、11辆车的速度震荡得到了有效的缓解,且能够更快地恢复到平稳状态;图4(b)表明,该震荡并未对后面车辆参数产生剧烈的影响,且该震荡幅度对后续车辆的影响逐渐减弱;图像4(c)显示,该控制器有效降低了车辆的车间距波动,使得车队运行更加平稳.在控制器作用前、后车辆的震荡时间和速度震荡幅度的对比如表1所示.从实验结果可知,该控制器确实能够有效地增强车辆的鲁棒性,车辆在遭受外部干扰时能够更快地恢复到平稳状态,验证了该控制器对抑制交通拥挤现象确实是有效的.

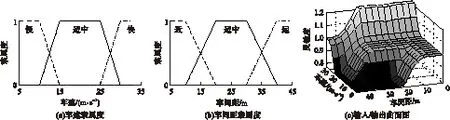
图2 车辆行驶速度和车间距的隶属度函数、输入/输出曲面图

Fig.2 Membership functions of speed and headway of vehicles and the input/output curved surfaces

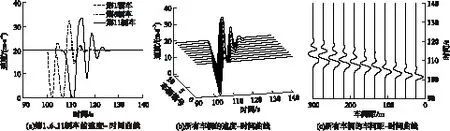
图3 在无控制器下车辆的速度-时间、车间距-时间曲线

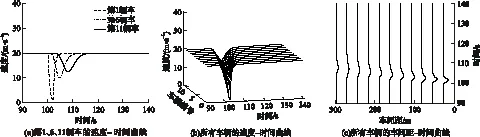
图4 在模糊控制器下车辆的速度-时间、车间距-时间曲线

表1 在第100秒至第200秒内所有车辆在模糊控制器作用前、后的震荡时间和震荡幅度比较

Table 1 Comparison of oscillation time and oscillation amplitude of velocity among all vehicles with or without controller from 100 s to 200 s

车辆编号 震荡时间/s 速度的震荡幅度/(m·s-1)无控制器有模糊控制器无控制器有模糊控制器19.008.3022.6618.37210.709.7025.1216.14313.9511.2027.5513.57414.9012.5030.0011.39517.7013.8031.969.65619.0015.1032.768.33721.9016.3033.037.40823.1017.3033.196.75924.3018.4033.306.281027.1019.5033.375.901129.9020.5033.415.59

文中对车辆在行驶过程中的能耗与排放问题进行研究.目前有关车辆能耗与排放问题的研究很多,且提出了很多排放模型,文中采用CO2排放模型[17]:

E=Kc(β1t′+β2L+β3Acc)

(17)

(18)

式中:E为二氧化碳排放量,kg;Kc为车辆的排放系数;βi(i=1,2,3)为距离系数;t′为车辆行驶时间;L为车辆的行驶距离;Acc为加速度增益量;vk为k时刻车辆的瞬时速度;δk为Heaviside函数,

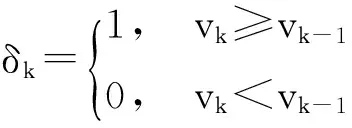
模糊反馈控制器作用前、后3辆车的二氧化碳排放量如图5所示.从图5(a)可知,在前车受到外部干扰且速度出现震荡时,车辆加、减速频繁,造成车辆二氧化碳排放激增;从图5(b)可知,采用文中设计的模糊反馈控制器,能够有效地降低车辆在受外部干扰时造成的额外的废气排放.

下面对所有车辆的二氧化碳排放情况进行分析,为了简化分析,当头车受到外部干扰时,把所有车辆在第90秒至第140秒内的二氧化碳排放量进行归一化处理,0和1分别表示在无控制器下所有车辆在第90秒至第140秒内二氧化碳排放的最大值和最小值,基于此所有车辆的废气排放情况如图6所示.从图中可知,文中设计的模糊控制器在外部干扰情况下能有效地抑制车辆的二氧化碳排放.

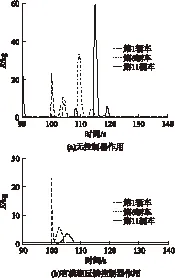
图5 模糊反馈控制器作用前、后3辆车的二氧化碳排放情况Fig.5 Carbon dioxide emissions of three vehicles with or without fuzzy controller

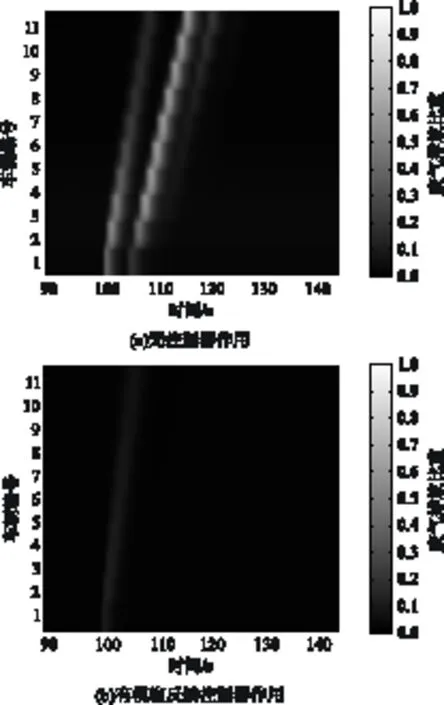
图6 模糊反馈控制器作用前、后所有车辆的二氧化碳排放情况

Fig.6 Carbon dioxide emissions of all vehicles with or without fuzzy controller

5 结论

由于驾驶员在车辆驾驶过程中受滞后反应时间的影响,且驾驶员的灵敏度在不同车间距和速度下会有所不同,为了准确描述车辆在行驶过程中的运行状态,文中提出了一类新的模糊滞后跟驰模型,对该模型的稳定性问题进行了分析,利用Lyapunov函数和并行分布补偿原理给出了模糊控制器存在的充分条件,即使得闭环模糊系统在控制器下满足稳定性,并通过求解LMI得到该模糊控制器.仿真实验表明,在该模糊控制器作用下,各车的速度震荡得到了有效的缓解,且能够更快地恢复到平稳状态,同时有效降低了车辆的二氧化碳排放量,从而验证了该方法在抑制交通拥堵和降低二氧化碳排放方面的可行性.文中方法可应用于自动驾驶中控制器的设计,由于文中方法是基于单车道,且车辆不允许超车,而实际情况中出现超车的现象十分普遍,故今后将对有超车行为的多车道的车辆跟驰问题进行研究,以适应更复杂的交通环境.

[1] CHEN Qun,WANG Yan.A cellular automata (CA) model for two-way vehicle flows on low-grade roads without hard separation [J].IEEE Intelligent Transportation Systems Magazine,2016,8(4):43-53.

[2] TANG T Q,CHEN L,YANG S C,et al.An extended car-following model with consideration of the electric vehicle’s driving range [J].Physica A Statistical Mechanics & Its Applications,2015,430:148-155.[3] LI Y,ZHANG L,ZHANG B,et al.Non-lane-discipline-based car-following model considering the effect of visual angle [J].Nonlinear Dynamics,2016,85(3):1-12.

[4] YUKAWA S,KIKUCHi M.Coupled-map modeling of one-dimensional traffic flow [J].Journal of the Physical Society of Japan,1994,64(1):35-38. [5] YUKAWA S,KIKUCHI M.Density fluctuations in traffic flow [J]. Journal of the Physical Society of Japan,1996,65(4):916-919.

[6] GE H X,LIU Y X,CHENG R J,et al.A modified coupled map car following model and its traffic congestion analysis [J].Communications in Nonlinear Science & Numerical Simulation,2012,17(17):4439-4445.

[7] HAN X,CHENG O,LI X.A modified coupled map car-following model considering a nonconstant driver sensitivity [J].Procedia Engineering,2012,31:1045-1049.

[8] ZHAO X,GAO Z.A control method for congested traffic induced by bottlenecks in the coupled map car-following model [J]. Physica A Statistical Mechanics & Its Applications,2006,366(C):513-522.

[9] FANG Y L,SHI Z K,CAO J L.Congestion phenomenon analysis and delayed-feedback control in a modified coupled map traffic flow model containing the velocity diffe-rence [J].Communications in Nonlinear Science & Numerical Simulation,2015,23(1/2/3):175-184.

[10] ZHANG L D,ZHU W X.Delay-feedback control strategy for reducing CO2emission of traffic flow system [J].Physica A Statistical Mechanics & Its Applications,2015,428:481-492.

[11] YU S,HUANG M,REN J,et al.An improved car-following model considering velocity fluctuation of the imme-diately ahead car [J].Physica A Statistical Mechanics & Its Applications,2016,449:1-17.

[12] PEI X,PAN Y,WANG H,et al.Empirical evidence and stability analysis of the linear car-following model with gamma-distributed memory effect [J].Physica A Statistical Mechanics & Its Applications,2016,449:311-323.

[13] KAZEMI R,ABDOLLAHZADE M.Introducing an evo-lving local neuro-fuzzy model:application to modeling of car-following behavior [J].ISA Transactions,2015,59(3):375-384.

[14] SAIFUZZAMAN M,ZHENG Z,MAZHARUL Haque M,et al.Revisiting the task-capability interface model for incorporating human factors into car-following models [J].Transportation Research Part B Methodological,2015,82:1-19.

[15] SCHULTZ G G.Analysis of distribution and calibration of car-following sensitivity parameters in microscopic traffic simulation models [J].Transportation Research Record Journal of the Transportation Research Board,2004,1876(1):41-51.

[16] KONISHI K,KOKAME H,HIRATA K.Coupled map car-following model and its delayed-feedback control [J].Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics,1999,60(4):4000-4007. [17] OGUCHI T,KATAKURA M,TANIGUCHI M.Carbon dixide emission model in actual urban road vehicular traffic condition [J]. Doboku Gakkai Ronbunshu,2002,695(695):125-136.

Feedback Control of a Class of Coupled-Map Fuzzy Time-Delay Car-Following System

ZHAICong1LIUWei-ming1TANFei-gang1,2

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China;2. School of Environment and Transportation, Shenzhen Institute of Information Technology, Shenzhen 518172, Guangdong, China)

When a driver is sensing headway, there exists a time-varying delay, and the sensitivity of the driver changes with the speed and the headway within a certain range. In order to accurately describe the running state of vehicles, on the basis of coupled-map car-following model, a new coupled-map fuzzy car-following model with time-delays is proposed, and the stability of the new car-following model is investigated. Then, by using Lyapunov function, the sufficient condition of the existence of a fuzzy controller is given. Under this condition, the closed-loop system achieves an asymptotic stability, that is, traffic congestion phenomena can be effectively suppressed. Finally, the fuzzy controller is obtained by solving a linear matrix inequality (LMI). Simulation results show that, with the help of the fuzzy controller, the car achieves smaller amplitude of velocity oscillation, faster process of recovering to an equilibrium state, and lower emission of carbon dioxide, which means that this method is effective in suppressing traffic congestion and reducing carbon dioxide emissions.

coupled-map car-following model; fuzzy control; time delay; stability; linear matrix inequality

1000-565X(2017)01- 0009- 09

2016-04-28

广东省科技计划项目(2014B090901012)

Foundation item： Supported by the Science and Technology Planning Project of Guangdong Province(2014B090901012)

翟聪(1989-),男,博士生,主要从事智能交通控制研究.E-mail:957083516@qq.com

† 通信作者： 刘伟铭(1963-),男,博士,教授,主要从事智能交通、高速公路收费系统研究.E-mail:weimingliu@126.com

TP 13

10.3969/j.issn.1000-565X.2017.01.002