基于复合稀疏约束的近似消息传递CS重构算法*
2017-04-25谢中华马丽红钟福平
谢中华 马丽红 钟福平
(华南理工大学 电子与信息学院, 广东 广州 510640)
基于复合稀疏约束的近似消息传递CS重构算法*
谢中华 马丽红†钟福平
(华南理工大学 电子与信息学院, 广东 广州 510640)
压缩感知(CS)重构中的近似消息传递(AMP)算法通过迭代执行小波阈值操作和残差更新来快速准确地实现稀疏信号重构,但它所采用的小波系数稀疏约束并不适用于非稀疏的自然图像,尤其CS观测过程存在噪声干扰时.为此,文中提出了一种基于复合稀疏约束和AMP框架的CS图像重构算法,使用相似图像块低秩约束和双边滤波约束作为自然图像的联合先验信息,以改善图像规则纹理和边缘的恢复效果,从而提升算法的重构性能.无噪CS观测的重构实验表明,文中算法的峰值信噪比(PSNR)比仅用低秩约束的AMP算法提高了0.45 dB,比原始AMP算法高6.19 dB;而在含噪CS观测的重构实验中,对应的PSNR增益则分别是0.25和4.60 dB;无论是无噪观测还是含噪观测,文中算法都获得了更佳的主观视觉效果.
压缩感知;近似消息传递;复合稀疏约束;低秩约束;双边滤波
压缩感知重构技术从低维观测值中恢复出高维的原始信号,其本质是求解一个欠定的线性方程组,而原始信号的稀疏性作为先验信息,提供观测值之外的附加信息量,可增加判断最优解的依据.小波稀疏性或梯度稀疏性常被用作信号的先验信息[1-3],前者提供了信号结构突变位置信息,后者则提供了沿最大变化方向的目标轮廓信息.但非稀疏的自然图像具有过多的突变位置和小目标轮廓,不具备小波和梯度稀疏特性.
为非稀疏信号构造变换系数间的高阶稀疏表示,可获得信号结构上的稀疏信息.高阶稀疏结构主要包括树稀疏[4-6]、块稀疏[7]和非局部稀疏[8-10].在基于树稀疏的CS重构算法中,WaTMRI算法[5]采用了小波树稀疏正则化项对具有父子关系的小波系数进行约束,使得它们趋向于共同为零或非零值;Turbo-AMP算法[6]通过条件概率表示小波系数的父子关系,并令父子系数共同为零或非零值的概率很大.父子系数具有相同稀疏样式的约定,对于整体结构规则的核磁共振图像或雷达图像十分有效,但不利于捕捉图像的局部变化特征,对局部突变明显的自然图像效果受限.为此,非局部稀疏结构被挖掘来描述相似图像块间的稀疏信息.文献[8]认为相似图像块组成的矩阵具有低秩的特性,应限定相似图像块的稀疏系数也相似,从而构建了一个基于图像块的低秩正则化模型;BM3D-AMP算法[9]通过概率图模型刻画CS观测值与原始信号间的统计关系,通过三维块匹配(BM3D)去噪算法对相似图像块进行阈值收缩处理,使其满足联合稀疏结构.但当参考块缺少相似块或受噪声干扰相似块匹配错误时,基于非局部稀疏的重构算法性能会下降,因为最终图像是重叠划分的多个重构图像块的加权平均结果,导致重叠区域的内容变得模糊.
以上分析表明,图像具有多种结构稀疏信息,但每种信息的适用范围有限.为提供更全面的自然图像的稀疏描述,文中在AMP框架[11]下构建一个由相似图像块低秩正则化约束项和双边滤波约束组成的复合稀疏模型.相似图像块的低秩约束负责图像规则纹理的恢复.双边滤波具有良好的边缘保持能力,能改善边缘模糊的问题.由于双边滤波算法在做邻域加权平均运算时同时考虑空间邻近信息和幅度相似性,使得离边缘较远的像素权值很小,从而保证了边缘附近像素值的保存.文中算法同时利用相似图像块的低秩特性和边缘像素的空间及幅值信息,以兼顾图像规则纹理和边缘的恢复.文中最后通过无噪观测和含噪观测实验来验证文中所提算法的性能.
1 近似消息传递算法
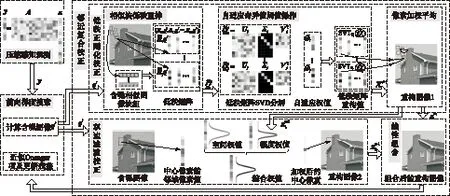
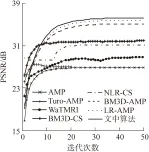
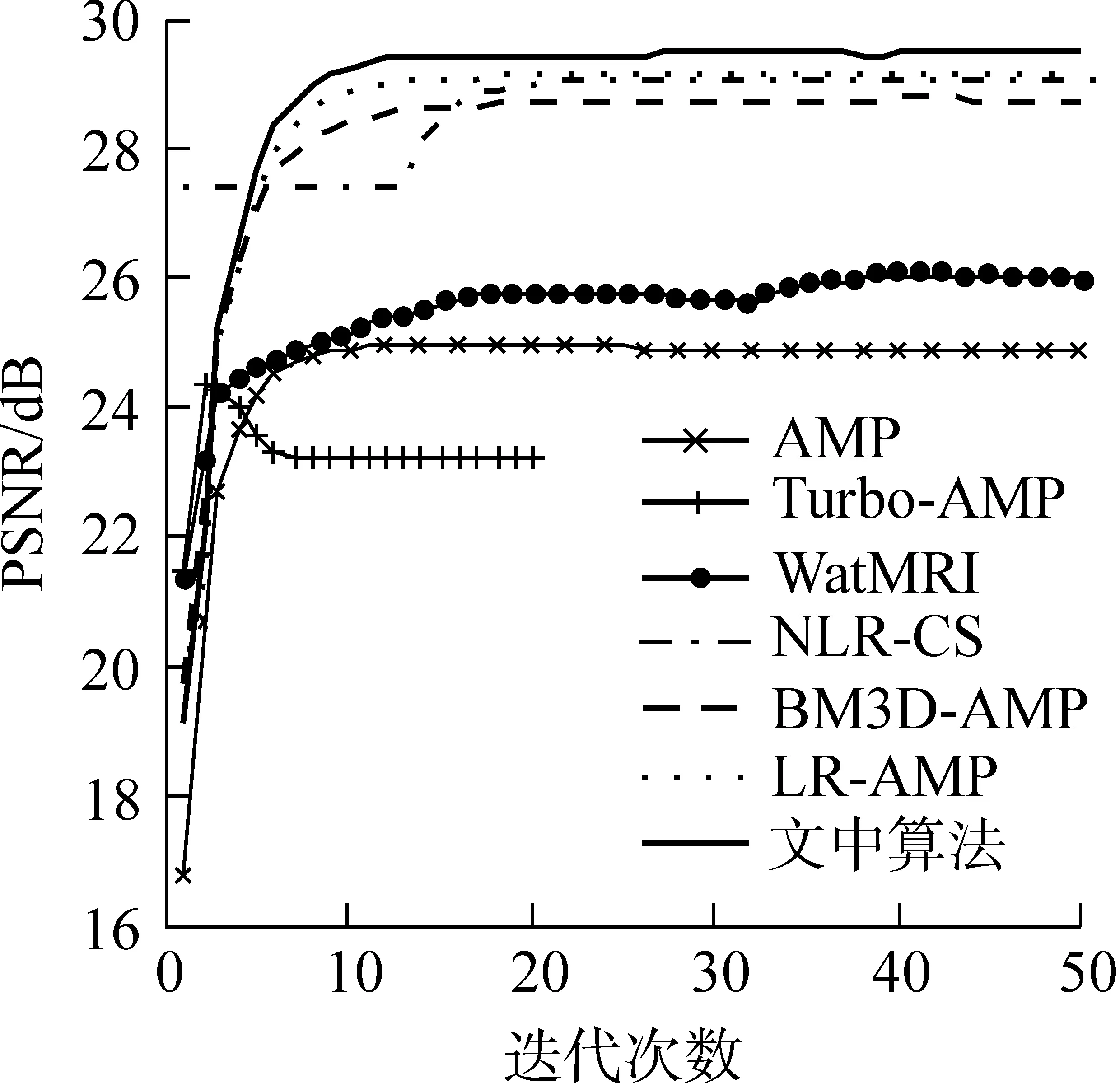
压缩感知重构技术从观测值y=Ax0(yCm)中估计原信号x0Cn,其中ACm×n是观测矩阵.由于m (1) 式中:第1项为数据保真项;第2项为稀疏约束项;‖x‖1为x的L1范数,等于其元素的绝对值之和;是控制保真项和约束项权重的正则化因子. 基于置信传播理论,近似消息传递(AMP)算法通过在与观测值y(或残差z)相关的因子节点和与信号x相关的变量节点间迭代传递概率消息来推断CS重构问题的最大后验概率[11].与一般的置信传播算法不同,在高维的情形下,AMP 算法利用中心极限定理及泰勒展开式来进行近似,极大地降低了计算量.从初始状态x0=0,z0=y开始,AMP算法求解目标函数(1)的迭代过程如下: xt+1=η(xt+A*zt) (2) (3) 式中,xt为原始信号x0在第t次迭代的估计值,η(y)为小波软阈值操作,为阈值参数,zt为第t次迭代的残差,A*为A的共轭转置.这里,残差zt比迭代阈值算法的残差y-Axt多了一个Onsager矫正项为阈值函数η的导数. 2.1 基于复合稀疏约束的图像CS重构新模型 自然图像中存在着丰富的相似成分,可当作CS重构算法的先验信息,即非局部稀疏结构.将图像重叠分块,以搜索窗为范围采用基于L2距离的块匹配方法[8]寻找相似图像块组,非局部稀疏约束使得组内的相似块具有相似的稀疏系数.另一方面,双边滤波具有良好的边缘保持能力,它通过兼顾空间邻近信息和幅度相似性的邻域加权,即边缘像素取较大的权值,保证了边缘附近像素值的保存.结合相似块低秩的特性与双边滤波的优点,文中构建基于复合约束的CS重构的新目标函数: (4) (5) 式中,Nv是以参考像素为中心的邻域,权值ku,v为 (6) 图1 相似块低秩约束与双边滤波约束复合的AMP算法流程图 2.2 基于复合分解技术的AMP算法 (7) (8) (9) 基于复合分解技术[14],该复合约束问题(qt) 通过变量分离和操作分离分解为两个易解的子问题,然后分别对子问题独立求解,再通过线性组合获得最终解.原始的复合分解技术[14]在做线性组合时使用了平均运算,而文中根据文献[15]中定理3.4使用更灵活的加权组合方式.基于复合稀疏模型的AMP重构算法描述如下. fort =1toTdo ∥Onsager项近似及残差更新 zt=y-Axt+zt-1‖′(xt-1+A*zt-1)‖1/m; qt=xt+A*zt;∥计算含噪图像 ∥低秩校正 ∥双边滤波校正 end for 其中,低秩校正的步骤是一个加权核范数最小化问题,等价于 (10) (11) 式(11)为一个加权核范数最小化问题,根据文献[8]中的定理1,式(11)的最优解可通过加权奇异值阈值(SVT)操作求得: (12) (13) (14) (15) (16) 这里图像块奇异值的零范数定义为奇异值个数之和.该值越小,表明这组重构后的图像块的稀疏程度越高,恢复效果越好,因此权值越大. 实施近似消息传递算法求解复合约束问题的一个难点在于Onsager校正项的估计,因为它需要计算邻近复合校正函数(qt)的导数(式(9)),而(qt)函数没有明确的输入输出关系.文中采用蒙特卡洛(MC)[17]随机数近似的方法来估计Onsager校正项1/m中的导数运算:((qt+εb)-(qt))/ε]≈ E[bT((qt+εb)-(qt))/ε] (17) 式中,E[·]表示求数学期望,独立同分布的随机矢量b~N(0,I),ε是一个很小的正数.具体步骤如下: (1)生成L个独立同分布的随机矢量b1,b2,…,bL; (2)对每个矢量bj计算估计值 (3)计算这些估计值的平均值 按照弱大数定理,当L→ ∞时,该估计值收敛到真实的导数值. 为验证文中算法的重构性能,分别在无噪观测和含噪观测两种情况下比较文中算法与其他7种算法(原始AMP算法、仅使用低秩正则化的AMP算法LR-AMP (即令文中算法的线性组合参数ω1=1,ω2=0)、基于树稀疏的算法WaTMRI[5]和Turbo-AMP[6]、基于非局部稀疏的算法NLR-CS[8]、BM3D-AMP[9]和BM3D-CS[10])重构的客观质量和主观质量.由于仅使用双边滤波的AMP 算法与文中算法的性能相差较大,因此未给出其重构结果.实验测试图像为图2所示的22幅128×128的自然图像.所有实验均在Matlab R2014a 平台上运行,使用的计算机CPU型号为AMD A10-5800K 3.80 GHz. 图2 实验所用的测试图像 3.1 无噪观测实验 在无噪环境下,采用8种算法分别在5个采样率(16%、18%、20%、22%和24%)下进行重构实验.由于采用随机观测方式,重构结果存在一些浮动,因此对每幅图像进行5次随机观测和重构,再计算PSNR的平均值,结果如图3所示.从图中可知:文中算法较其他算法有更佳的客观重构质量;基于非局部稀疏的5种重构算法(包括文中算法、LR-AMP、NLR-CS、BM3D-AMP、BM3D-CS)比WaTMRI、Turbo-AMP和原始AMP算法的PSNR平均值更高,说明非局部稀疏约束比树稀疏结构或小波稀疏约束更适合于自然图像的重构;与仅用低秩正则化的LR-AMP算法相比,文中算法获得了高的PSNR平均值,说明在低秩约束的基础上使用复合约束能进一步提升AMP算法的重构性能.事实上,文中算法的PSNR比LR-AMP算法平均提高了0.45dB,而比原始AMP算法平均提高了6.19dB.由于采用高阶稀疏结构,文中算法改善了原始AMP算法的重构质量;又因为复合约束的合理引入,文中算法比基于非局部稀疏的其他4种算法具有更优的重构质量. 图3 不同采样率下8种算法的PSNR平均值 Fig.3AveragePSNRof8algorithmsatdifferentsamplingrates 以Cameraman图像为例,在20%采样率下8种算法的重构结果如图4所示,PSNR随迭代次数的变化曲线如图5所示.从图4可知,基于非局部稀疏的5种算法重构的图像依然比基于树稀疏约束的两种算法和原始AMP算法更整洁、更清晰.在基于非局部稀疏的5种重构算法中,文中算法和LR-AMP算法在细节纹理(如草地区域)方面恢复得更好.这归功于文中建立的基于加权核范数的低秩正则化模型,以及自适应的核范数权值设定.文中算法与LR-AMP算法的区别可通过分别计算它们和原图对应像素的差值,再取绝对值得到的图像进行对比得出.如在衣服边缘区域,文中算法重构图像的白色像素比LR-AMP算法少,说明与原图像的差异更小,因此,引入双边滤波约束能增强原始重构算法的边缘保持能力. 图4 20%采样率下8种算法对Cameraman图像的重构结果 由于文中算法整体上基于AMP框架,且在求解复合约束问题时应用了复合分解技术,因此可以保证算法收敛.从图5可知,到达相同PSNR结果时文中算法所需迭代次数比LR-AMP算法少,说明复合约束比单独低秩约束能进一步缩小解空间,从而加快最优解的搜索速度.由于BM3D-CS和NLR-CS的迭代次数(分别为100和260)远多于其他算法,为集中显示所有算法,图中这两种算法只分别给出间隔为2和间隔为5的PSNR结果. 图5 20%采样率下7种算法的PSNR随迭代次数的变化曲线 Fig.5 Changing curves of PSNR with the iteration number of 7 algorithms at 20% sampling rate 3.2 含噪观测实验 现实环境中压缩感知观测普遍存在噪声的干扰,为了说明使用复合约束能提升AMP算法对噪声的鲁棒性,文中比较了8种算法在含噪观测情况下的重构质量.在实验中先对CS观测结果加入高斯噪声,即y=Ax0+w,其中w为高斯噪声,然后使用上述CS重构算法进行重构.以采样率20%为例,在4种噪声标准差σ(1、5、10和15)下7种算法的PSNR平均值如图6所示.由于每次迭代时用观测得到的傅里叶系数替换重构后的系数,本质上无法去除观测值中的噪声,故本次实验没有使用BM3D-CS算法.从图6可知,添加噪声后各算法的PSNR值普遍略低于未加入噪声时的结果(其中σ=10时文中算法比无噪时平均降低了3.79 dB),但与无噪情况下观察到的规律相似:基于非局部稀疏的4种重构算法的PSNR平均值比基于树稀疏约束的两种算法和原始AMP算法高;在所有采样率下文中算法的PSNR平均值仍然最高,文中算法的PSNR比仅使用低秩正则化的LR-AMP算法平均提高了0.25 dB,比原始AMP平均提高了4.60 dB.这些结果进一步验证了在无噪情况下分析得到的结论,进一步说明文中构造的复合约束模型能提升AMP算法对噪声的鲁棒性. 图6 不同噪声强度下7种算法的PSNR平均值 在噪声方差为10和20%采样率下7种算法对Cameraman图像的重构结果如图7和图8所示.和图4相比,图8中每种算法的重构图像质量都下降了,但基于非局部稀疏的4种算法的重构图像依然比基于树稀疏约束的两种算法和原始AMP算法更整洁,视觉效果更好.在基于非局部稀疏的4种重构算法中,NLR-CS算法重构图像的噪声点更多,BM3D-AMP算法重构图像的细节(如相机的支架区域)更加模糊,LR-AMP算法和文中算法的重构结果较为理想.类似地,通过和原图像的差值图像比较,可以发现文中算法重构图像在边缘处的白色像素比LR-AMP算法少,即与原图像的差异更小,因此,文中算法在边缘保持上优于LR-AMP算法.以上结果表明,在CS观测中存在噪声干扰时,文中算法依然能保持最佳的重构质量. 图7 在σ=10和20%采样率下7种算法的PSNR随迭代次数的变化曲线 Fig.7 Changing curves of PSNR with the iteration number of 7 algorithms at 20% sampling rate andσ=10 图8 在σ=10和20%采样率下7种算法对Cameraman图像的重构结果 文中提出了一种基于复合稀疏约束和近似消息传递框架的图像压缩感知重构算法.基于加权核范数的相似图像块低秩约束和基于边信息指导的双边滤波约束组成的复合稀疏约束提升了AMP算法对图像规则纹理和边缘的重构质量.此外,复合分解技术的运用实现了复合约束问题的简易求解.无噪观测和含噪观测实验结果表明:与仅用相似块低秩约束算法相比,文中算法采用的复合稀疏约束能进一步增强图像边缘的保持能力;无论是无噪观测还是含噪观测,文中算法的重构质量均优于原始AMP算法及其他基于结构化稀疏模型的重构算法,验证了复合稀疏约束对提升AMP算法性能的有效性.事实上,复合稀疏约束不仅限于文中所采用的低秩约束和双边滤波约束,而文中主要是给出了在AMP框架下如何使用复合稀疏约束的一种解决措施. [2] BECK A,TEBOULLE M.A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems [J].SIAM Journal on Imaging Sciences,2009,2(1):183-202. [3] 曾春艳,马丽红,杜明辉.前向预测与回溯结合的正交匹配追踪算法 [J].华南理工大学学报(自然科学版), 2012,40(8):14-19. ZENG Chun-yan,MA Li-hong,DU Ming-hui.Look ahead and backtracking-based orthogonal matching pursuit algorithm [J].Journal of South China University of Technology(Natural Science Edition),2012,40(8):14-19. [4] HE L,CARIN L.Exploiting structure in wavelet-based Bayesian compressive sensing [J].IEEE Transactions on Signal Processing,2009,57(9):3488-3497. [5] CHEN C,HUANG J.Exploiting the wavelet structure in compressed sensing MRI [J].Magnetic Resonance Imaging,2014,32(10):1377-1389. [6] SOM S,SCHNITER P.Compressive imaging using appro-ximate message passing and a Markov-tree prior [J].IEEE Transactions on Signal Processing,2012,60(7):3439-3448.[7] ELDAR Y C,KUPPINGER P,BOLCSKEI H.Block-sparse signals:uncertainty relations and efficient recovery [J].IEEE Transactions on Signal Processing,2010,58(6):3042-3054.[8] DONG W,SHI G,LI X,et al.Compressive sensing via nonlocal low-rank regularization [J].IEEE Transactions on Image Processing,2014,23(8):3618-3632.[9] METZLER C,MALEKI A,BARANIUK R G.BM3D-AMP:a new image recovery algorithm based on BM3D denoising [C]∥Proceedings of IEEE International Conference on Image Processing.Quebec City:IEEE,2015:3116-3120.[10] DABOV K,FOI A,KATKOVNIK V,et al.Image denoi-sing by sparse 3-d transform-domain collaborative filtering [J].IEEE Transactions on Image Processing,2007, 16(8):2080-2095. [11] DONOHO D L,MALEKI A,MONTANARI A.Message passing algorithms for compressed sensing [J].Procee-dings of the National Academy of Sciences,2009,106(45):18914-18919. [12] VENKATAKRISHNAN S,BOUMAN C A,WOHLBERG B.Plug-and-play priors for model based reconstruction [C]∥Proceedings of IEEE Global Conference on Signal and Information Processing.Austin:IEEE,2013:945-948.[13] XIE Z,MA L,ZENG X.A structured AMP method recovering signals with a forward-backward splitting mode [C]∥Proceedings of IEEE Region 10 Conference. Macao:IEEE,2015:1-4.[14] HUANG J,ZHANG S,METAXAS D.Efficient MR image reconstruction for compressed MR imaging [J].Medical Image Analysis,2011,15(5):670-679. [15] COMBETTES P L,PESQUET J C.A proximal decomposition method for solving convex variational inverse problems [J].Inverse Problems,2008,24(6):1-27. [16] DONG W,SHI G,LI X.Nonlocal image restoration with bilateral variance estimation:a low-rank approach [J].IEEE Transactions on Image Processing,2013,22(2):700-711. [17] METZLER C,MALEKI A,BARANIUK R G.Optimal recovery from compressive measurements via denoising- based approximate message passing [C]∥Proceedings of IEEE International Confence on Sampling Theory and Applications.Washington D C:IEEE,2015:508-512. An Approximate Message Passing Algorithm with Composite Sparse Constraint for CS Reconstruction XIEZhong-huaMALi-hongZHONGFu-ping (School of Electronic and Information Engineering, Guangzhou 510640, Guangdong, China) In CS reconstruction, approximate message passing (AMP) can realize the reconstruction of sparse signals quickly and accurately by performing both wavelet de-noising and residual updating iteratively. However, the sparse constraints of the wavelet coefficients used in AMP are not suitable for non-sparse natural images, especially when the measuring process of CS is disturbed by noises. In order to solve this problem, a CS image reconstruction algorithm is proposed on the basis of composite sparse constraints and an AMP framework. This algorithm takes both the low-rank constraint of similar image patches and the bilateral filter constraint as the joint prior information of natural images to enhance the recovery effect of image textures and edges, thus improving the performance of the algorithm. The results of the reconstruction experiment with no noise in the measuring process of CS show that, the proposed algorithm averagely improves PSNR (Peak Signal to Noise Ratio) by 0.45 dB and 6.19 dB, respectively in comparison with the AMP algorithm that only uses low-rank constraint and the original AMP algorithm. While in the presence of noise, the corresponding average PSNR gains are respectively 0.25 dB and 4.60 dB. In conclusion, the proposed algorithm can achieve a better visual quality whether it is noiseless or not. compressed sensing; approximate message passing; composite sparse constraint; low-rank constraint; bilateral filter 1000-565X(2017)01- 0018- 08 2016- 05- 10 国家自然科学基金资助项目(61471173) Foundation item: Supported by the National Natural Science Foundation of China(61471173) 谢中华(1985-),男,博士生,主要从事压缩感知、多维信号重建研究.E-mail:eezhxie@gmail.com † 通信作者: 马丽红(1965-),女,博士,教授,主要从事图像视频信号处理、模式识别研究.E-mail:eelhma@scut.edu.cn TP 391 10.3969/j.issn.1000-565X.2017.01.003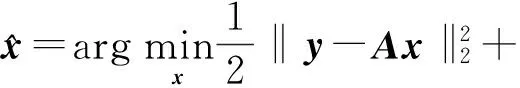
2 基于复合稀疏约束的AMP算法



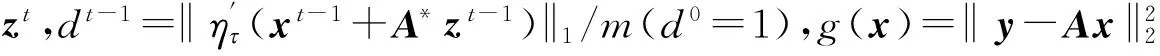

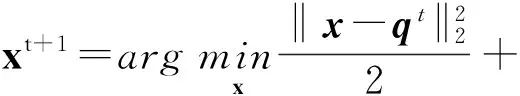

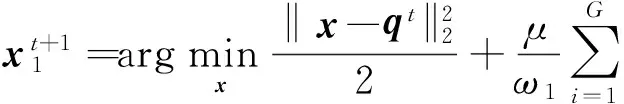
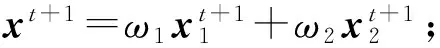
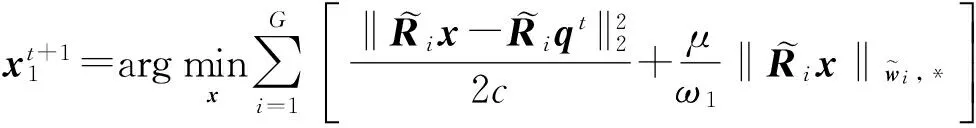
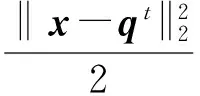
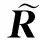



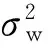
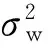

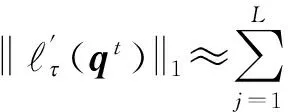
3 实验与结果分析





4 结论
