星箭解锁分离装置中摆臂的动力学分析

蒋青飞，徐洋，岳洪浩，汪国元，钱如峰

（1.东华大学机械工程学院，上海201620；2.哈尔滨工业大学机电工程学院，哈尔滨150001）

星箭解锁分离装置中摆臂的动力学分析

蒋青飞1，徐洋1，岳洪浩2，汪国元1，钱如峰1

（1.东华大学机械工程学院，上海201620；2.哈尔滨工业大学机电工程学院，哈尔滨150001）

在非火工甚低点式星箭解锁分离装置工作过程中，要求星箭分离在很短的时间内完成以及避免在星箭分离过程中产生较大的冲击力对其他重要的敏感元器件造成损害，因此在星箭解锁分离装置中摆臂旋转时间及由其与圆柱壳体碰撞产生的碰撞力对于整个分离过程的影响是不可忽略的。主要通过运用动力学及Herz接触理论对星箭解锁分离装置中一级摆臂、二级摆臂进行动力学建模及分析，运用数值分析软件对模型进行仿真计算，得出摆臂旋转时间和碰撞冲击力的仿真曲线，并通过实验验证理论模型的正确性；仿真分析结果与试验结果对比表明数据规律一致性较好，计算结果具有较高的可信度。

振动与波；星箭解锁分离装置；摆臂；旋转时间；碰撞力

太空飞行器上需要许多解锁分离装置来实现空间连接与解锁的功能，比如星箭分离、火箭级间分离、有效载荷的分离释放等[1]。分离装置一方面保证在发射过程中可靠连接，另一方面确保在入轨后可靠分离，在实现正常分离的同时，需要保证解锁分离过程产生的碰撞冲击力不会对其他元器件的使用造成影响。与传统火工分离装置相比，非火工分离装置具有冲击小，无污染等特点，另外还具有容易检测、试验成本低的特点，产品在试验后可部分或完全重复使用。目前对于物体间的碰撞问题已经是众多工程领域的基础性研究内容，比如在航空航天[2]、机器人控制[3]、工程机械和散体材料[4]等领域有比较广泛的应用。建立正确而又合理的模型，能够准确地对系统进行运动学和动力学分析，弄清物体之间的碰撞力学机制是非常有意义的。

文中所分析的对象是一种新型非火工星箭解锁分离装置，该装置采用形状记忆合金为驱动源，通过电加热的方式实现触发动作，从而实现整套装置的分离功能。在分离装置动作的过程中，一级摆臂和二级摆臂的限位依次被解除，在扭簧的驱动下运动旋转，并分别与圆柱壳体发生碰撞，形成两次冲击。主要对摆臂分离运动过程进行分析，研究摆臂运动规律以及摆臂与壳体之间的碰撞力。

1 摆臂的动力学分析

星箭解锁分离装置摆臂工作原理为当形状记忆合金丝(SMA)驱动及控制组件接收上面级供电后，电能转变成热能，由于SMA具有应变特性，当达到SMA的相变温度时，SMA产生回复应力和应变，从而带动触发转轴转动，从而解除对一级摆臂的限位，一级摆臂在扭簧扭矩M1作用下旋转，进而解除对二级摆臂的限位，二级摆臂在扭簧扭矩M2作用下转动，实现分离，图1所示为星箭分离装置及摆臂示意图，图1(a)为分离装置实物模型，图1(b)为分离装置中摆臂示意图，初始时刻限位块限制一级摆臂转动，一级摆臂受到扭矩M1的作用，二级摆臂受到扭矩M2的作用。

1.1 摆臂旋转特性分析

对星箭分离装置中摆臂分离过程进行简化，如图2所示。图2(a)表示触发转轴未转动、摆臂限位没有解除时的状态，图2(b)表示摆臂限位解除后的运动状态，图2(c)表示摆臂与圆柱壳体碰撞后的状态。

1.1.1 一级摆臂动力学分析

当t＞0时，触发转轴转动，一级摆臂限位被解除，对一级摆臂进行受力分析，摆臂受到扭簧扭矩以及运动副中的反力FRx、FRy的作用，如图3所示。由受力平衡可得式(1)。

式中Fx、Fy为一级摆臂的惯性力。一级摆臂的运动微分方程组为

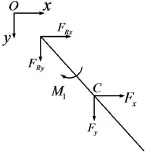
图3 一级摆臂转动受力分析

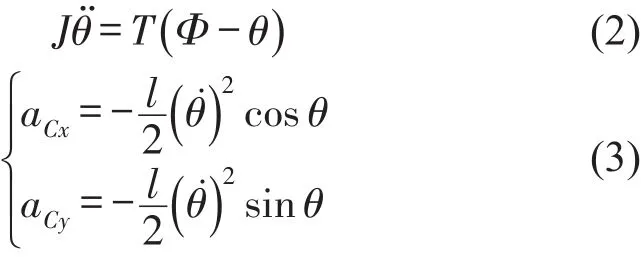
式中aCx、aCy为一级摆臂质心C的加速度；Φ为初始时刻扭簧扭转角，为72度；θ为时间t的函数，J为一级摆臂转动惯量，T为扭簧的扭转刚度系数3.571 4 N∙mm/(°)。m为一级摆臂的质量，为0.001 45 kg，一级摆臂的长度为28 mm。

求解式(2)中的2阶常系数线性非齐次微分方程

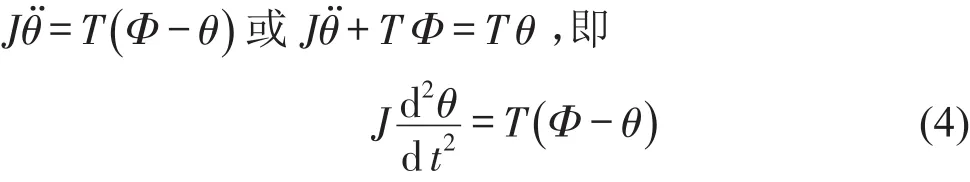
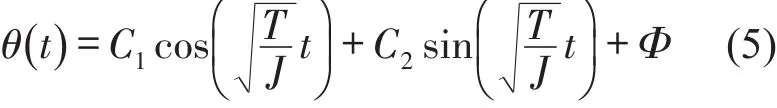
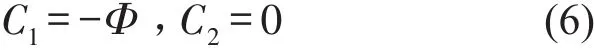
则对应的角位移函数为

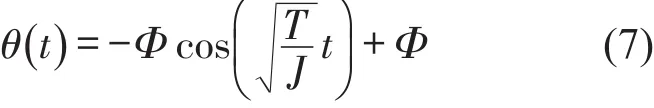
经计算可得式(4)对应的通解为

经测得一级摆臂与壳体之间夹角约为68度，通过计算可知一级摆臂从开始旋转到与圆柱壳体碰撞的时间约为0.023 s，通过计算可得一级摆臂顶端处沿水平方向和垂直方向速度为vx=-1.924 5 m/s，vy=1.317 7 m/s。

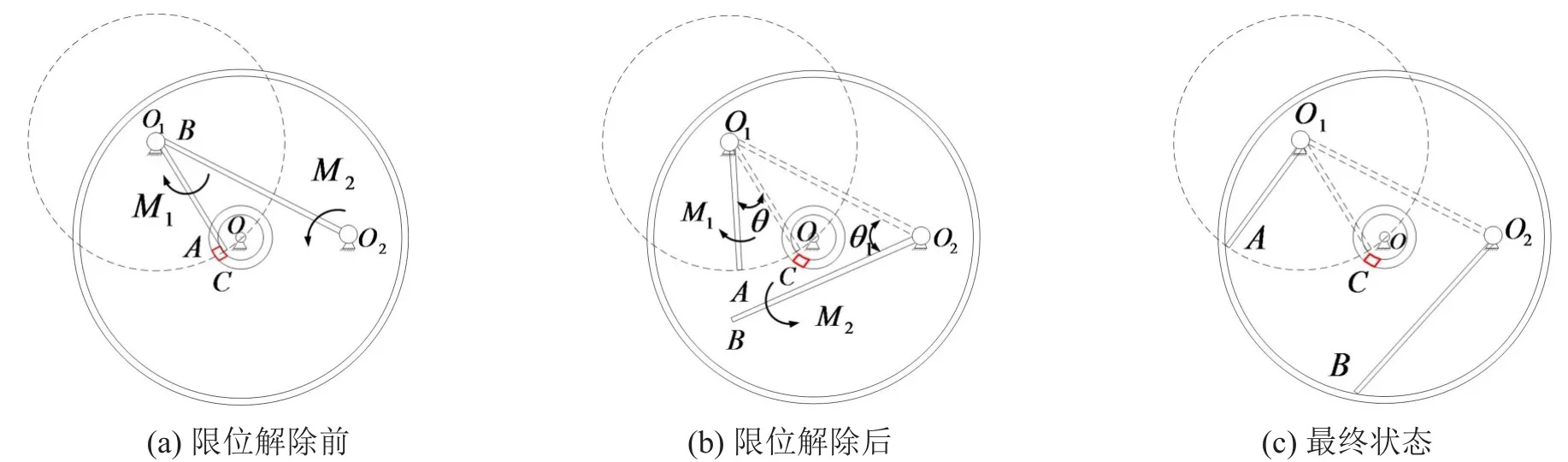
图2 摆臂分离过程示意图

1.1.2 二级摆臂动力学分析

由于二级摆臂臂端受到一级摆臂的限位作用，只有当一级摆臂转动对其解除限位后，二级摆臂才能转动，则二级摆臂转动受力分析如图4所示。

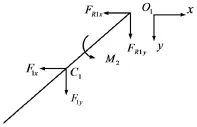
图4 二级摆臂转动受力分析

二级摆臂在转动过程中受到扭簧力矩的作用、转轴对摆臂的支反力FR1x、FR1y的作用。则可得转动过程中受力平衡方程

式中F1x、F1y为二级摆臂受到的惯性力。

二级摆臂的运动微分方程为

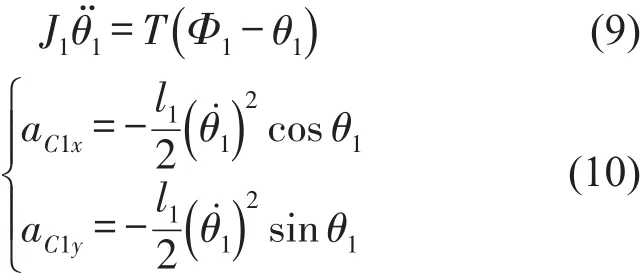
式中aC1x、aC1y为二级摆臂质心C的加速度；Φ1为扭簧从起始点位置旋转过的角度，为80度；θ1为时间t的函数，J1为二级摆臂转动惯量，T为扭簧的扭转刚度系数，为3.571 4 Nmm/(°)。m1为二级摆臂的质量，为0.012 86 kg，摆臂2的长度l1为48 mm。

可得二级摆臂对应的角位移函数为

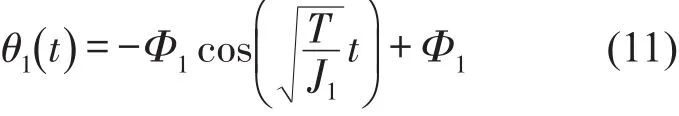
测得二级摆臂与圆柱壳体之间夹角约为76度，则根据式(11)计算可得二级摆臂从开始旋转到与圆柱壳体碰撞的时间约为t=0.08 s。二级摆臂顶端沿水平方向和垂直方向速度分别为v1x=-0.912 8 m/s，v1y=0.713 1 m/s。

1.2 摆臂碰撞特性分析

通常来讲对于多体系统接触碰撞问题，一般有三种处理方式：经典碰撞理论、等效弹簧阻尼模型和连续接触模型。等效弹簧阻尼模型假定两质体的碰撞为点接触，质体之间的碰撞力通过接触点作用在质体上，碰撞力的大小取决于等效弹簧的刚度特性和阻尼特性，等效弹簧阻尼模型虽然是一种近似分析的方法，但使用起来方便，并且当等效刚度和等效阻尼的参数选择合理时，计算结果也很准确，目前应用比较普遍[5]。Khulief和Shabana提出运用线性弹簧阻尼模型近似模拟多体系统碰撞过程的方法，从而将线性弹簧阻尼模型引入到多体系统碰撞动力学的研究中，建立了含弹性碰撞力模型的多体动力学方程，并给出了确定等效质量、弹簧刚度以及阻尼系数的理论方法[6]。从图2(c)中可以看出，摆臂与圆柱壳体碰撞是一种斜碰撞，因此，在计算碰撞力时将碰撞力分解为法向接触力和切向接触力，利用等效弹簧阻尼接触模型进行摆臂撞击圆柱壳体动力学分析建模。

1.2.1 建立接触模型

(1)建立碰撞时的法向碰撞接触模型

两质体碰撞时，考虑到材料的阻尼，其法向碰撞接触模型用等效弹簧阻尼模型进行描述，则可得碰撞期间法向接触力，用广义的Hertz公式形式表示为[7]

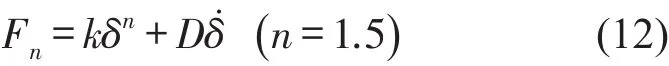
式中Fn为碰撞点处法向接触力；k为弹性力学中Hertz刚度，取决于材料特性和曲率半径；δ为接触点的法向压缩量,̇为接触点法向相对速度；D为与δ有关的阻尼系数为恢复系数，v0为撞击点的初始相对速度。

(2)建立碰撞时的切向碰撞接触模型

摆臂与圆柱壳体的碰撞为斜碰撞，如图5所示，故会有切向运动的产生。当摆臂与圆柱壳体碰撞后的运动状态为相对滑移时，此时摩擦模型可以选择Coulomb摩擦定律，滑动摩擦力与正压力成正比，方向与相对运动速度的方向相反。

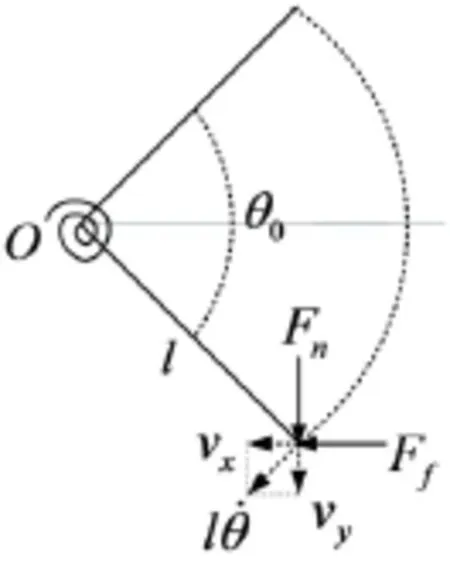
图5 摆臂与传动壳体碰撞模型

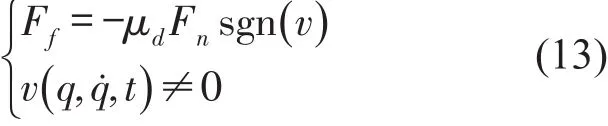
式中Ff为接触处的滑动摩擦力；μd为动摩擦系数；为接触点的相对滑动速度。当摆臂与传动壳体碰撞后的运动状态为静止模式时，则切向接触力Ff小于两质体间的最大静摩擦力，故有

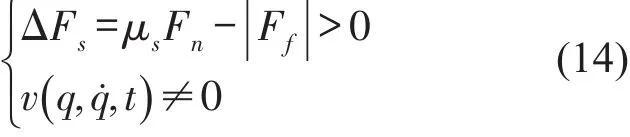
式中ΔFs为撞击处的静摩擦力与动摩擦力之差；μs为静摩擦系数。考虑到两接触体的切向变形，切向接触力的计算方法为

式中ε(t)为接触点处的切向弹性变形，当有相对滑动时，ε(t)为常数，K为等效切向刚度。由于切向摩擦力的处理异常复杂，目前还没有统一有效的解决方式，而且大多数情况下都不考虑切向静止状态的摩擦力，故仅仅考虑相对滑动时的摩擦力，并采用Coulomb摩擦定律计算。

1.2.2 系统碰撞动力学方程

假定摆臂与圆柱壳体间的法向接触力与Y轴平行，通过牛顿欧拉方法可得摆臂与传动壳体碰撞前运动阶段的系统动力学方程为

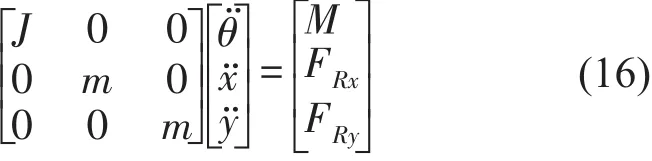
当摆臂与圆柱壳体碰撞时，需在动力学方程中加入等效接触力，则系统动力学方程变为

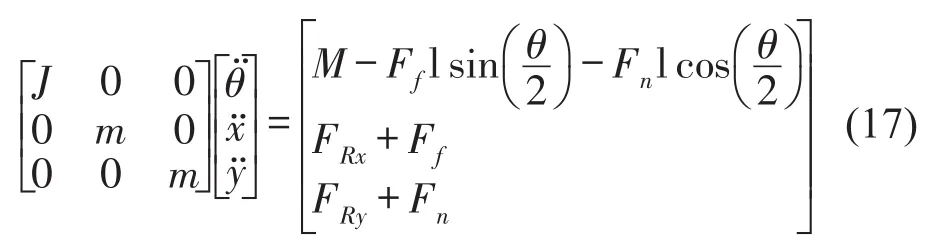
利用所建立的动力学模型对整个分离碰撞过程进行数值模拟，可得图6至图10所示的各模型仿真图。

分析图6可知，一级摆臂从开始运动到与圆柱壳体碰撞所用的时间大约为0.023 s，这一时间符合星箭解锁分离装置摆臂瞬时分离的要求，一级摆臂旋转角度约为68度，摆臂与壳体碰撞后经历了两次反弹，回弹最大角位移约为15度；而且从图6(a)中可以看出，二级摆臂解除限位后，与圆柱壳体碰撞所用时间大约为0.08 s，旋转角度约为76度，回弹最大角位移约为10度；图6(b)中一级摆臂的角速度也在增加，但随着时间的增加，其增加速率变缓，这一点也正符合摆臂与旋转壳体碰撞时不会产生过大碰撞冲击力的要求，二级摆臂运动情况类似，相对一级摆臂来说，角速度增加缓慢，摆臂与壳体碰撞后回弹，角速度发生突变，由于一级摆臂质量相比二级摆臂质量轻，从图6(b)中可以看出一级摆臂碰撞后反弹角速度比二级摆臂大；从图6(c)、图6(d)中可以看出，一级摆臂的转动使得扭簧扭转角减小，扭矩减小，可以看到角加速度在逐渐减小。一级摆臂在0.023 s时刻、二级摆臂在0.08 s时刻与壳体碰撞，角加速度发生突变，摆臂与壳体碰撞阶段接触时间很短，从图6 (c)、图6(d)中可以看出首次碰撞瞬间摆臂角加速度值比未碰撞前摆臂角加速度高出许多。

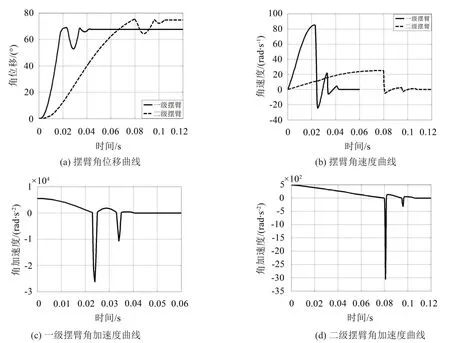
图6 摆臂的运动分析曲线

分析图7、图8可知，摆臂与壳体未碰撞前，触发转轴解除对一级摆臂的限位后，支点O对一级摆臂的支反力随摆臂旋转角度变大逐渐增大，在t= 0.017 s左右时，X轴方向的支反力值达到最大，约为0.19 N，在t=0.023 s左右时，Y轴方向上的支反力值约为0.29 N，此时X轴方向反力已减小约为0.12 N，而且支反力均连续变化。二级摆臂约在0.058 s左右，X轴方向支反力达到最大约为0.125 N。在0.08 s时，碰撞前一瞬间Y轴方向支反力最大，约为0.22 N。摆臂与壳体碰撞阶段，支点对摆臂的支反力发生两次突变，碰撞结束后，由于一级摆臂和二级摆臂各自的扭簧扭矩不为零，从图7、图8中可以看摆臂依旧受到支点对其的支反力。

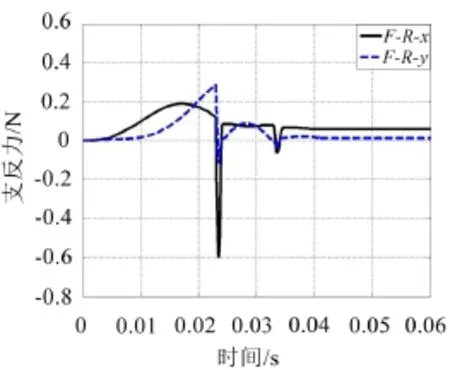
图7 支点O对一级摆臂的支反力FRx、FRy

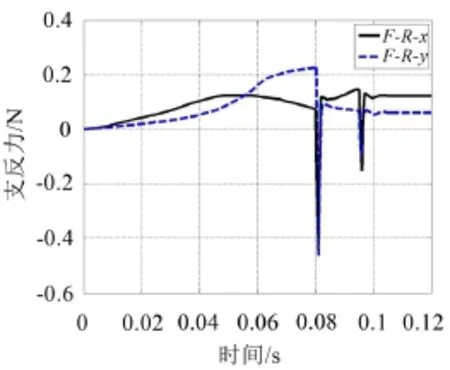
图8 支点O1对二级摆臂的支反力FR1x、FR1y

从图9中可知一级摆臂与壳体撞击时，瞬间碰撞力的大小约为375 N左右。在图10中显示二级摆臂与壳体碰撞时，碰撞力的大小约为430 N。

2 实验验证

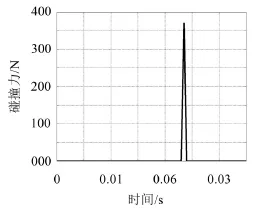
图9 一级摆臂与壳体碰撞碰撞力仿真图

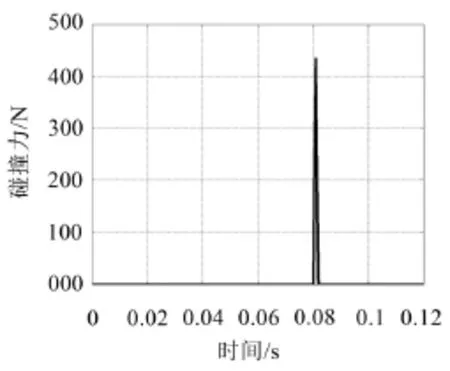
图10 二级摆臂与壳体碰撞产生的碰撞力仿真图

实验采用东华测试公司DH 5992通用型动态测试分析系统对星箭分离装置分离过程进行数据采集，设置采样频率为10 kHz，为避免固定约束的干扰，实验在悬挂方式下进行，同时为了保证能准确采集数据，实验中采用超薄微型压电式力传感器进行冲击力的测试，传感器位置布置在摆臂与壳体接触点处，如图11所示。

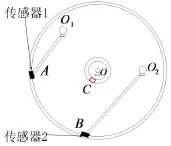
图11 测试传感器位置

得到摆臂从分离到与圆柱壳体碰撞的数据，选取首次碰撞的数据进行绘图可得碰撞阶段产生的碰撞力大小以及所对应的时间值。分析图12、图13可知，一级摆臂与壳体碰撞时间约为0.023 s，一级摆臂与壳体碰撞力约为312 N，二级摆臂与壳体碰撞力约为345 N。在误差允许的范围内，仿真结果与实验所测结果基本吻合，仿真与实验结果有差别的原因主要是对模型进行简化时所选的参数值为近似值。

3 结语

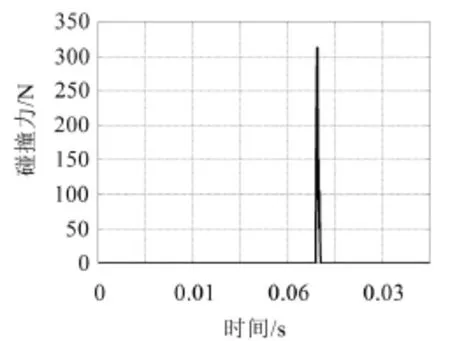
图12 一级摆臂与壳体碰撞力测试图

图13 二级摆臂与壳体碰撞力测试图

通过对星箭分离装置中一级摆臂、二级摆臂进行动力学建模、仿真分析，得出两摆臂在分离过程中碰撞前后的受力、位移、速度的变化情况，同时也得知一级摆臂从开始转动到与壳体碰撞所需时间约为0.023 s，二级摆臂从开始转动到与圆柱壳体碰撞所需时间约为0.08 s以及碰撞冲击力的大小。从而可知摆臂的尺寸形状、材料及所加初始扭矩都会对整个分离装置的分离造成不可忽略的影响，并通过实验验证了所建模型的正确性。

[1]高滨.形状记忆合金在航天器分离机构上的应用[J].航天返回与遥感，2005，26(1)：48-52.

[2]刘锦阳，洪嘉振.空间伸展机构接触的动力学分析[J].宇航学报，1997，18(3)：14-25.

[3]华卫江，章定国.柔性机器人系统碰撞动力学建模[J].机械工程学报，2007，43(12)：222-228.

[4]马炜.散体介质冲击载荷作用下力学行为理论分析与算法实现[D].北京：北京大学，2008.

[5]白争锋.含间隙机构接触碰撞动力学研究[D].哈尔滨：哈尔滨工业大学，2007.

[6]KHULIEF Y A,SHABANA A A.A continuous force model for the impact analysis of flexible multibody systems[J].Mechanism and Machine Theory,1987,22 (3):213-224.

[7]王巍，孙京，于登云，等.基于接触理论的一类带锁定机构的间隙铰链分析模型研究[J].宇航学报，2004，25(1)：1-12.

DynamicsAnalysis of SwingArms in the Satellite-rocket Unlocking and Separation Device

JIANG Qing-fei1,XUYang1,YUE Hong-hao2, WANG Guo-yuan1,QIAN Ru-feng1
(1.College of Mechanical Engineering,Donghua University,Shanghai 201620,China; 2.College of Mechanical and Electrical Engineering,Harbin Institute of Technology, Harbin 150001,China)

In the working process of the non-pyrotechnic and lower point-to-point impact satellite-rocket unlocking and separation device,the swing arm rotation time and the impact force generated by the collision cannot be ignored for the whole separation process.In this paper,the dynamics and Herz contact theory are used to the dynamic modeling and simulation of the first and second stage swing arms in the separation device by means of the numerical analysis software. The simulation curves of the swing arm rotation time vs.impact force are obtained,and the correctness of the theoretical model is verified by experiments.The mutual comparison between the simulation results and the experimental results shows that the data consistency is good.The calculation results have a high reliability.

vibrationandwave;satellite-rocket unlocking and separation device;swing arm;rotation time;impact force

O3；TB123

A

10.3969/j.issn.1006-1355.2017.02.0010

1006-1355(2017)02-0047-06

2016-10-30

蒋青飞（1992－），男，安徽省阜阳市人，硕士生，主要研究方向为机械系统振动、冲击及模态分析。

徐洋，女，博士生导师。E-mail:xuyang@dhu.edu.cn