基于离散事件仿真的多状态多阶段任务系统可靠性分析

苏续军, 吕学志

(1.军械工程学院 一系， 河北 石家庄 050003； 2.陆军炮兵训练基地 模拟训练中心， 河北 宣化 075100)



基于离散事件仿真的多状态多阶段任务系统可靠性分析

苏续军1, 吕学志2

(1.军械工程学院 一系， 河北 石家庄 050003； 2.陆军炮兵训练基地 模拟训练中心， 河北 宣化 075100)

介绍了多状态多任务系统可靠性参数的离散事件仿真算法。对多阶段任务系统及其特点进行了分析，提出了利用表决冷储备(AS)树描述多阶段任务系统每个阶段的逻辑结构关系。利用状态图分析了多状态多阶段任务系统的行为。依据离散事件仿真思想，分别给出了多状态多阶段任务系统的仿真算法，具体介绍了算法的假设条件、输入参数、输出参数、算法框架、如何描述AS树、如何确定系统状态、如何确定单元转移状态。给出了计算实例，验证了该算法的正确性和有效性。该仿真算法可以很好地描述多阶段任务系统复杂行为，可以获得多种了解系统运行规律的可靠性参数，具有很强的通用性与实用性。

系统评估与可行性分析； 可靠性; 多阶段任务系统； 离散事件系统仿真

0 引言

多阶段任务系统(PMS)是指可以根据系统配置、任务成功标准、子系统行为的差异将系统的任务周期分成一系列连续不相交的独立时间段的系统。而这些连续不相交的独立时间段则被定义为阶段。它自1975年由Esary等[1]提出以来，引起了许多学者的关注和研究。现在的PMS任务可靠性分析方法大致可分为两类：解析法和仿真法。解析法主要包括基于马尔可夫的方法[2]和基于二元决策图(BDD)法[3]。前一种方法基于随机过程的理论进行分析，可能存在状态空间爆炸的问题，限制了其实际应用。后一种方法只适用于不可修的PMS. 由于解析法描述和求解能力存在不足，仿真法得到了更多青睐，得到了广泛的应用。按照开发层次，仿真可以分为仿真模型、一次开发仿真程序和二次开发仿真程序。聂成龙等[4]建立了基于Petri网的PMS任务效能多层仿真模型。一次开发仿真主要是指在编程语言基础上开发的仿真程序，如Murphy等[5]开发的Raptor仿真工具可完成对PMS可靠性仿真。二次开发仿真是指在第三方仿真工具基础上开发的仿真程序。杨建军等[6]提出基于Extend的多态PMS仿真模型。杨春辉等[7]应用着色Petri网(CPN)工具建立PMS的多层通用仿真模型。仿真模型是仿真程序的概念模型；一次开发仿真程序较为灵活，工作量较大；二次开发仿真程序工作量较少，但受第三方仿真工具在建模能力方面的限制。现有的仿真法仍在建模能力方面存在局限，表现为只描述两状态单元，任务阶段系统可靠性关系不能涵盖冷储备关系，这影响了其应用范围。本文主要针对现有仿真法存在的问题，提出解决方法。

1 多阶段任务系统及其特点

随着现代系统变得越来越复杂和智能化，系统的运行不再是单一过程，而是包括了多个功能流程的转换，或者在不同阶段通过对单元重组形成新系统的过程，这样的系统称之为PMS[8]。根据很多文献的论述，PMS两个基本特点：系统功能的实现依赖于时间连续且不重叠的多个任务阶段；任务成败标准具有阶段依赖性。PMS经常被配置到关键应用中，特别是航天和军用装备领域，如巡航导弹系统、防空武器系统及航天测控系统等，这些系统中对于任务可靠性都具有很高的要求。同时，PMS任务可靠性分析对于发现系统薄弱环节、改进设计、合理分配可靠性指标等都具有重要的作用。因此，基于PMS的可靠性建模与分析也逐渐成为研究的热点。作者认为每个任务阶段系统可靠性关系，即任务成败标准是建模重点。但是目前的仿真方法主要用BDD[7]、最小路集[9]、最小割集[10]、故障树[11]来描述系统可靠性关系，这种描述方法很难反映单元状态的相关性和多样性，并不适用于冷储备这种状态相关的可靠性逻辑关系，限制了其应用范围。这里采用表决冷储备(AS)树来表示任一任务阶段系统可靠性关系。

如图1所示，在AS树中，有两种图形，分别为矩形和圆形。矩形表示下层单元的关系，矩形中的“A”表示表决关系，“S”表示冷储备关系。如果是表决关系，矩形中数字表示k/n(A)表决系统中的k，k是工作单元数，n是系数中总的单元数。如果是冷储备关系，矩形中数字表示冷储备系统n-k/n(S)中正常工作单元数k. 圆形表示下层单元，按数字顺序进行编号。在图1中，单元1、2、3组成1/3(G)表决系统，单元4、5、6组成有2/3(S)冷储备系统(3个单元中有2个备件)，1/3(G)表决系统与2/3(S)冷储备系统又构成1/2(S)冷储备系统。使用AS树描述任务阶段可靠性关系有以下4个优势：1)容易建立。很容易从扩展可靠性框图转化为AS树；2)建模能力强。可以描述串、并联、表决、冷储备等关系组成的复杂可靠性关系；3)可以很容易描述系统配置。PMS中，每个阶段工作的单元可能是不同的，AS树含有工作单元的信息，即系统配置信息；4)利于编写仿真算法。在具体介绍算法时，将会看到这种建模方法在确定系统状态和单元转移状态方面的优势。

图1 任务阶段AS树状图示例Fig.1 AS tree of mission phase example

2 多状态多阶段任务系统行为分析

在分析PMS可靠性时，为了简单起见通常假设单元有工作和故障两个状态。但是当要考虑冷储备关系时，就必须考虑单元的待用状态。此外，当系统故障时，单元也没有必要处于工作状态，需要进入待用状态。为了分析PMS行为，首先分析一下典型的2单元串、并联系统与2单元冷储备系统的行为。图2是2单元串联系统状态图，图2中x1与x2分别表示两个单元，sys表示系统。x1、x2有3个状态：work (工作)、down(故障)、wait(待用)；sys有2个状态：work (工作)、down(故障)。x1、x2与sys的初始状态为工作状态；当x1、x2任一故障之后，系统故障。f1、f2分别表示x1、x2的故障事件；g1、g2分别表示x1、x2的修好事件。当单元x1或x2处于work状态，当sys进入down状态，即en(sys.down)，则x1、x2进入wait状态。当单元x1或x2处于wait状态，当sys进入work状态，即en(sys.work)，则x1或x2进入work状态。当发生故障事件后，x1或x2由work状态转变为down状态。当发生修好时间后，x1或x2由down状态转变为wait状态。图3是2单元并联系统状态图。图2和图3的区别主要是sys的状态转换条件不同。图4是2单元冷储备系统状态图。x2是备件，x1、sys的初始状态为工作状态，x2初始状态为待用状态；当x1故障之后，x2进入工作状态；当x2与x1都故障时，系统故障。通过比较图5、图3、图4，可知冗余系统中，单元状态是相关的。当系统故障时，可以正常工作的单元也将进入待用状态。当系统正常工作时，处于待用状态的单元也将进入正常工作状态。此外，在冷储备系统中，由于某些单元是备用的，所以单元之间状态是相互影响的[12]。

图2 串联系统状态图Fig.2 State diagram of series system

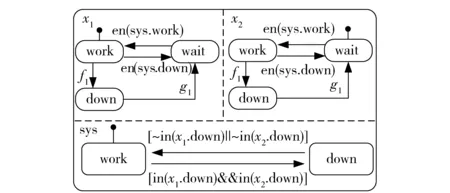
图3 并联系统状态图Fig.3 State diagram of parallel system

图4 冷储备系统状态图Fig.4 State diagram of cold-standby system

接下来，以图1所示的冗余系统对具有两层嵌套结构的冗余系统行为进行分析。假设单元1、单元2、单元3、单元4、单元5、单元6初始状态为工作，处于第2层的1/3(A)表决系统处于工作状态，2/3(S)冷储备系统处于工作状态，则顶层的1/2(S)冷储备系统处于工作状态。顶层系统状态处于工作状态，由于其关系是冷储备，所以处于第2层的1/3(G)表决系统、2/3(S)冷储备系统必有一个处于待用状态，选择2/3(S)冷储备系统处于待用状态，则其下属单元4、单元5、单元6处于待用状态。若单元1、单元2、单元3都故障且没有修好，第2层的1/3(G)表决系统进入故障状态，2/3(S)冷储备系统处于待用状态，启动2/3(S)冷储备系统后顶层的1/2(S)冷储备系统仍处于正常工作状态，选择2/3(S)冷储备系统下属单元4处于工作状态，单元5、单元6处于待用状态。

通过以上分析，可以得出以下结论：对于PMS的某个任务阶段，其行为总是由单元的事件引起的，单元故障或修好事件再影响到上层关系的状态，间接影响到兄弟单元状态。这样的行为变化具体来讲分为两个过程：一个过程是“自下而上”确定系统状态的过程；另一个过程是“自上而下”确定单元转移状态的过程。以上的分析是建立仿真算法的基础。

3 仿真算法设计

3.1 假设条件

算法假设条件有：1)系统功能的实现依赖于时间连续且不重叠的多个任务阶段；2)单元3状态：单元有3个状态，即工作、故障、待用；否则单元状态仍然是两个；3)系统两状态：在任一时间，系统或者故障或者工作；4)单调关联系统：所分析的系统认为是单调关联系统，也就是说，如果每个单元处于工作状态，系统必定处于工作状态，如果没有单元处于工作状态，系统必定处于不工作状态，单元从不工作状态向工作状态转变不会导致系统从工作状态向不工作状态转变；5)单元之间状态相关；6)任务阶段系统结构：每个任务阶段系统的逻辑结构已知，可以用AS树的形式给出；7)单元的故障分布函数与维修时间分布函数：每个单元的故障分布函数与维修时间分布函数已知，即分布类型与分布参数已知；8)维修策略：对于每个单元采用连续状态监视策略，以及事后维修策略，不考虑维修资源有限性；9)单元修复后如新：当单元故障后经过维修，或用新单元更换之后，单元如同新的一样。

3.2 输入输出参数

输入参数主要包括：1)仿真次数：增加仿真次数一方面可以提高结果的精确性，另一方面也将消耗更多的计算时间与内存资源；2)仿真时间：每次仿真的逻辑时间；3)单元数量；4)单元故障分布函数；5)单元维修时间分布函数；6)任务阶段数量；7)每个任务阶段持续时间；8)任务阶段系统结构，以AS树形式表示。

输出参数[13]主要包括：

1) 任务可靠性R，

(1)

2) 平均可用度A0，

(2)

3) 战备完好性RED，

(3)

4) 可用与可靠概率PAR，

PAR=平均使用可用度×可靠度；

(4)

5)平均首次任务失效间隔时间MTBMF，

(5)

式中：yi为每i次仿真中，系统第一次失效前的工作时间，如果任务没有失效，则yi等于任务的时间长度；

6)系统的平均工作(可用)时间MUT和系统的平均故障(不可用)时间MDT，

(6)

(7)

3.3 算法框架

该算法使用离散事件仿真(DES)方法，主要的事件包括单元故障、单元修好、任务开始事件，如图5所示。算法步骤[14]如下：

第1步：初始化仿真变量，即仿真时钟与统计变量。

第2步：初始化事件表，即安排第一个任务阶段开始事件。

第3步：确定下一个事件的类型，发生时间，如果是故障事件和修好事件则确定发生部位。

第4步，判断事件是故障，是修好，还是阶段开始。若是故障事件，则采用故障事件操作；若是修好事件，则采用修好事件操作；若是阶段开始事件，则采用阶段开始事件操作。

第5步，更新系统状态、统计变量，推进仿真时钟。

第6步：重复步骤3～步骤5，直到达到仿真时间。

第7步：记录单次仿真数据。

第8步：重复步骤1～步骤7，直到满足仿真次数要求。

图5 PMS可靠性仿真算法Fig.5 Simulation algorithm of PMS reliability

下面对事件流程进行介绍，图6是故障事件流程。首先，根据维修时间分布函数生成维修时间，安排单元未来事件为修好事件(可以理解为维修结束时刻，单元修好)，然后确定系统新状态st(1)，若有st(1)为正常工作，则确定单元状态，更新单元事件表，更新单元状态；否则，所有处于工作状态单元处于备用状态，更新事件表，记录单元剩余寿命。图7是修好事件响应操作流程图。首先，单元处于备用状态，更新事件表，单元剩余寿命为0，然后确定系统新状态st(1)，若st(1)为正常工作，则确定单元状态，更新单元事件表，更新单元状态。图8是任务开始事件响应操作流程图，主要是根据任务阶段的可靠性关系初始化系统状态、单元状态和事件表，安排下一任务开始事件。以上介绍了仿真算法框架，接下来介绍算法中的一些细节问题。

图6 故障事件响应操作流程图Fig.6 Flow chart of failure event response

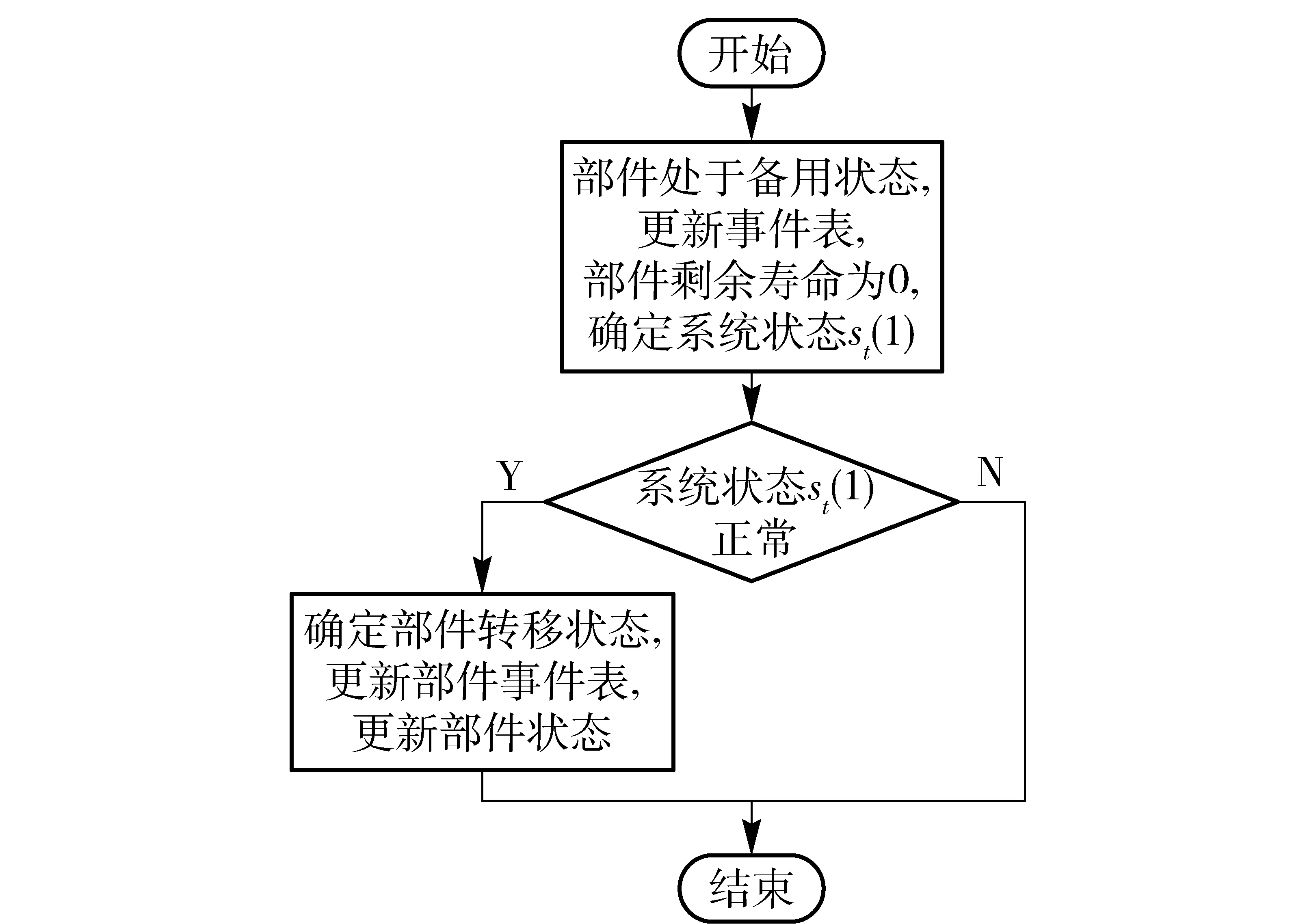
图7 修好事件响应操作流程图Fig.7 Flow chart of repairing event response

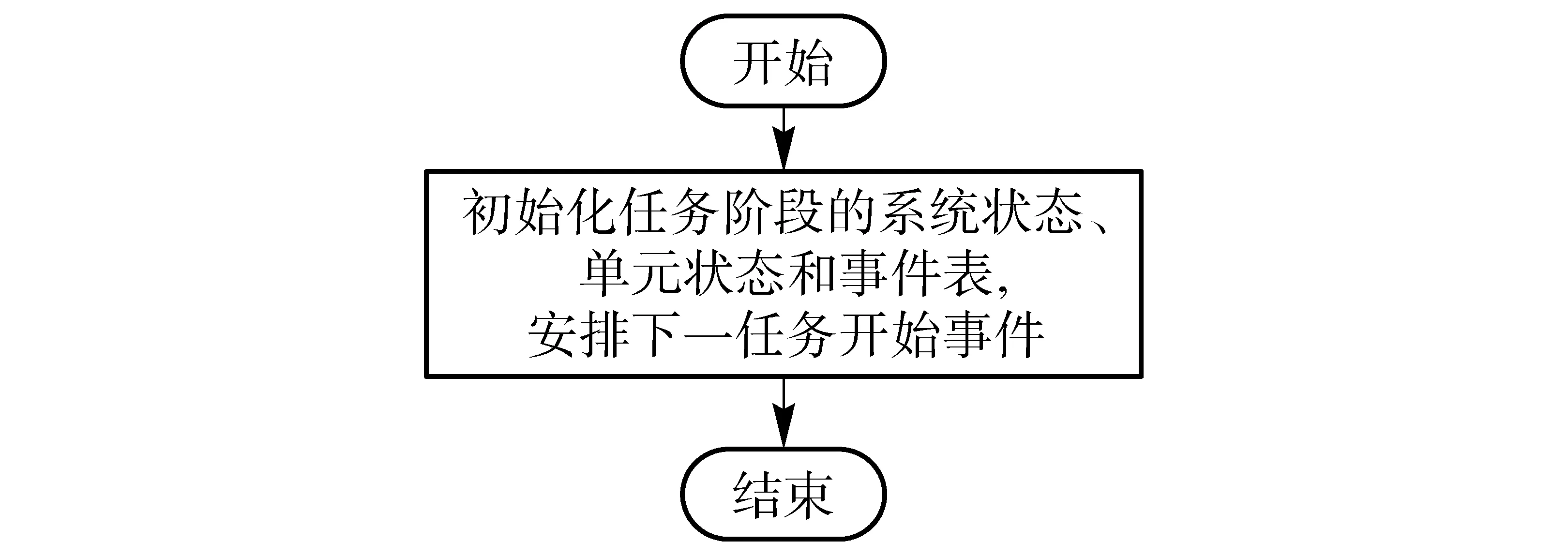
图8 任务开始事件响应操作流程图Fig.8 Flow chart of mission start event response

3.4AS树的描述及常用方法

首先，来看一下AS树应该采用哪种数据结构。显然，AS树可以用树来描述。树有两种主要表示方法，一种是左子结点/右兄弟结点法，另一种是父指针表示法[15]。这里介绍后一种表示法。图9所示的AS树可以表示为三维数组形式。

图9 树的父指针数组表示法Fig.9 Parent pointer presentation method of tree

在父指针表示法中，每个结点包含类型值和标记值，以及一个指向父结点的指针。为简明起见，父指针表示为父结点在数组中位置的下标值。类型值可以取1、2、3，取1表示结点为表决关系结点，取2表示结点为冷储备关系结点，取3表示结点为单元。标记值对于不同类型结点有不同含义。对于表决关系结点，标记值为k/n(A)表决系统中的k. 对于冷储备关系结点，标记值为n-k/n(S)冷储备系统中的k. 对于单元结点，标记值为单元编号。在具体仿真计算过程中，用类来描述树，并定义树的方法。这些方法主要包括判断结点i是否是叶子isleaf(i)，得到宽度搜索向量breadthfirstiterator，得到结点的子结点向量getchildren(i)，得到结点类型值gettype(i)，得到结点标记值getmark(i).

3.5 确定系统状态算法

正如前面的分析，确定系统状态是一个“自下而上”的过程。输入参数包括t(描述系统结构的AS树)和sc(描述所有单元状态的向量)。输出参数是st(描述AS树所有结点状态的节点)，st(1)表示BS根结点状态，即系统状态。确定系统状态的流程图如图10所示，其中sign()是一个函数，当x=0时，sign(x)=0；当x非0时，sign(x)=x/|x|.

图10 确定系统状态流程图Fig.10 Flow chart of determining system state

3.6 确定单元转移状态

确定单元转移状态是一个“自上而下”的过程。只有确定了系统状态为工作的情况下才会确定单元转移状态。若系统状态为故障，则令所有处于工作状态的单元进入待用状态。算法的输入参数包括t(描述系统结构的AS树)和sc(描述所有单元状态的向量)。输出参数是s′c(描述所有单元转移状态的向量)。对于类型是冷储备关系且转移状态为工作(即等于1)的结点，可以称其为“A型”结点，确定其子结点的转移状态较为复杂(流程图从上向下第3个“判定”符号左下部分)。首先，对于“A型”结点的子结点，按照转移状态可以分为两类：一是不可能转移状态的子结点，主要是处于故障状态的子结点；二是可能转移状态的子结点，包括处于工作状态、待用状态的子结点。

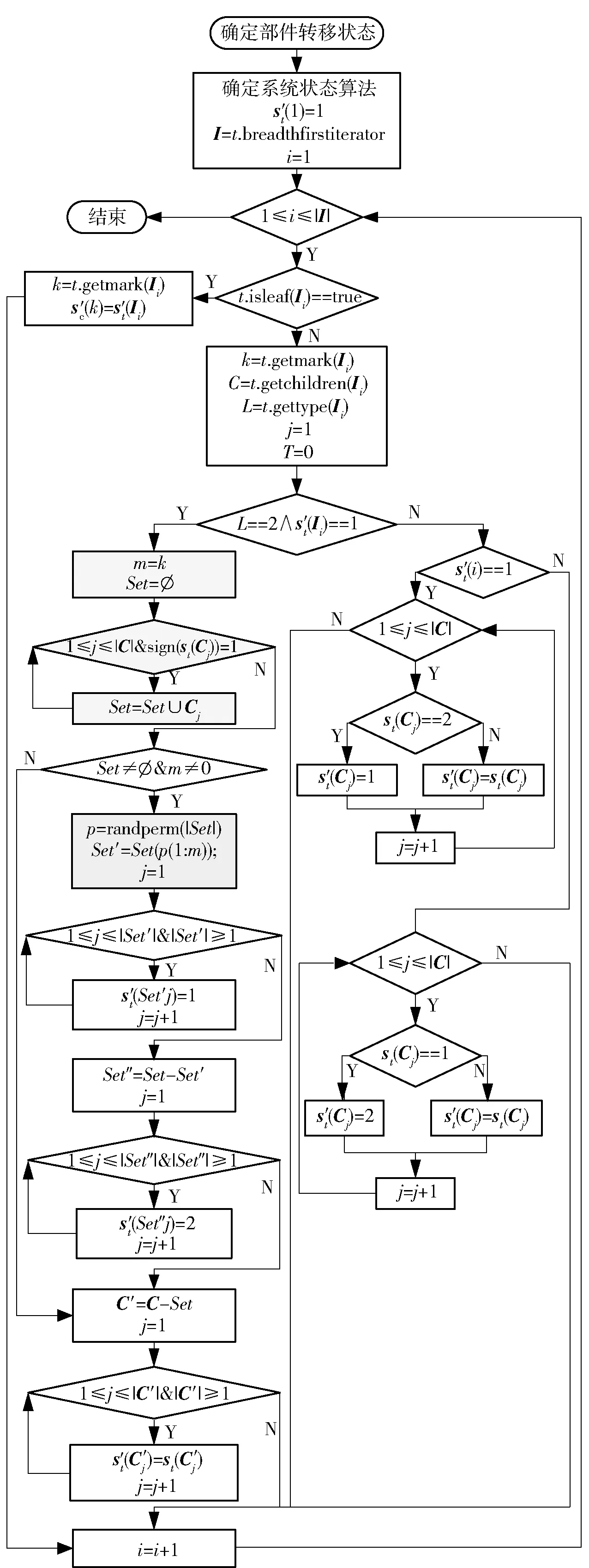
图11 确定单元转移状态流程图Fig.11 Flow chart of determining transition state of unit

在图11中，以5%灰度为背景色的框图部分是“确定待转移状态子结点集合”。这里采用的策略1，即处于故障状态的子结点不可能转移状态，而处于工作、待用状态的子结点可能转移状态。当然，也可能采用策略2，即处于故障、工作状态的子结点不可能转移状态，而处于待用状态的子结点可能转移状态。采用策略2确定待转移状态集合的算法如图12所示。在具体编程时可以将这两种策略用“分支结构(switch)”组合在一起。之后，从待转移状态子结点集合中确定哪些子结点处于工作状态，哪些子结点处于待用状态，可称该过程为“启动方式”。在图11中，以10%灰度为背景色的框图描述了该过程。这里采用策略1，即随机启动方式。当然，也可能采用策略2，即优先启动方式。这种方式按照某种优先顺序启动子结点，如图13所示。对于不是“A型”结点的结点，可将其称为“B型”结点。对于“B型”结点，确定其子结点的转移状态较简单(见图11，从上向下第3个“判定”符号右下部分)。如果结点转移状态为1，则所属子结点中处于待用状态的子结点进入工作状态。如果结点转移状态为0，则所属子结点中处于工作状态的子结点进入待用状态。

图12 策略2流程图Fig.12 Flow chart of Strategy 2

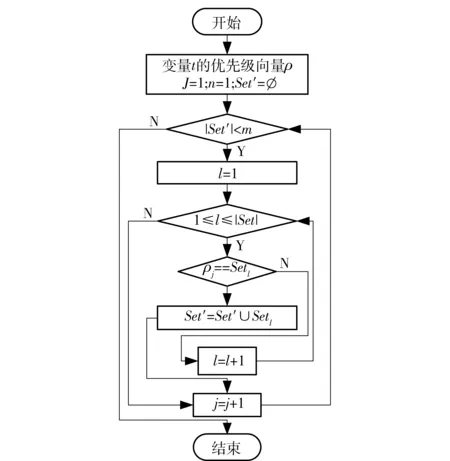
图13 优先启动流程图Fig.13 Flow chart of prioritized startup

4 计算实例

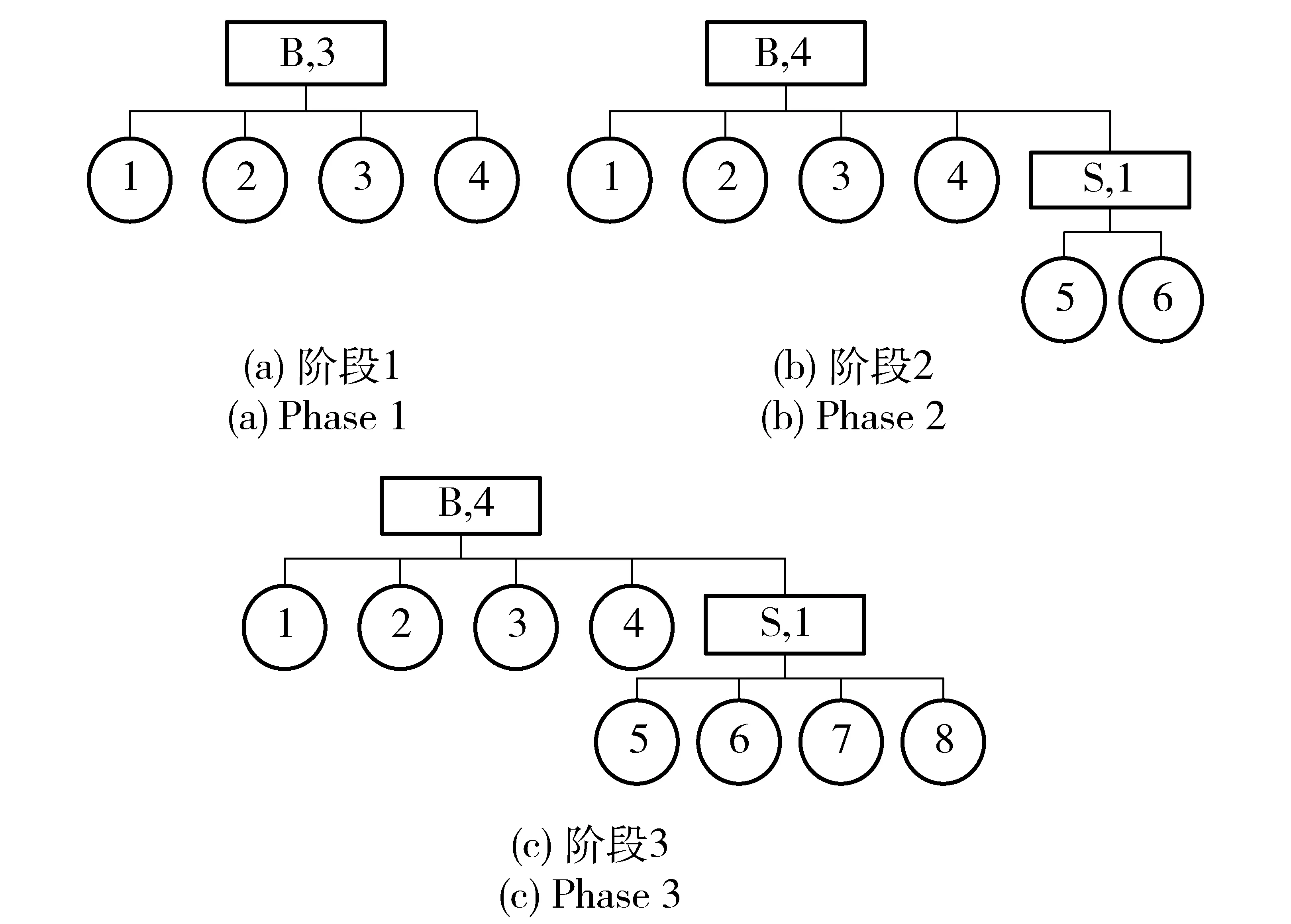
图14 3个任务阶段的系统AS树Fig.14 AS tree of three mission phases

系统由8个相同单元组成，其故障分布函数均为e-0.01t,t≥0，修理时间分布函数均为1-e-0.1t,t≥0. 时间单位为小时。PMS有3个任务阶段，3个任务阶段持续时间分别为10 h、15 h、20 h，不同任务阶段系统的结构用上文的AS树表示，如图14所示。根据本文所提出的算法设计用Matlab进行了编程，评估PMS的可靠度。可靠度仿真的次数1 000次。任务可靠性R为0.803 0. 平均可用度A0为0.983 9. 平均可用时间MUT为162.798 3 h，平均不可用时间为2.900 5 h. 每次仿真可用时间和不可用时间直方图与累积概率分布曲线如图15、图16所示。如果没有任务时间的限制，可用时间和不可用时间通常会近似服从正态分布，而有了任务时间限制后，可用时间和不可用时间服从“截断的”正态分布。每次仿真首次任务失效间隔时间直方图与累积概率分布区域如图17所示。原理同上，首次任务失效间隔时间也服从“截断的”正态分布。平均任务首次失效间隔时间MTBMF为211.720 7 h. 战备完好性RED为0.926 9. 每次仿真维修时间与维修次数的直方图如图18所示，维修时间呈指数分布，而维修次数呈泊松分布，平均维修时间MTTR为9.800 3 h. 故障次数直方图与累积概率分布曲线如图19所示，呈泊松分布，平均故障次数为0.263.

图15 系统可用时间统计分析图Fig.15 Statistic analysis of system available time

图16 系统不可用时间统计分析图Fig.16 Statistic analysis of system unavailable time

图17 平均首次任务失效间隔时间统计分析图Fig.17 Statistic analysis of mean time between mission failure

图18 维修时间与次数直方图Fig.18 Histogram of repairing time and times

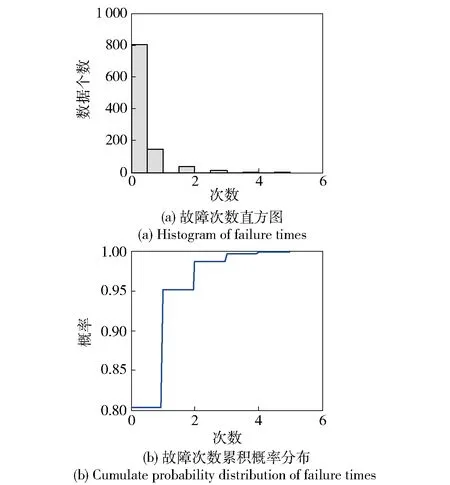
图19 故障次数统计分析图Fig.19 Statistic analysis of failure times

5 结论

本文针对现有PMS可靠性仿真只考虑单元0～1状态，不能适应于存在冷储备关系的情况，不能处理单元可能存在故障、正常(工作与待用)3种特殊状态且状态相关的情况，利用AS树状结构来描述任务阶段系统可靠性关系；依据离散事件系统仿真思想，给出了PMS可靠性仿真算法，介绍该算法的假设条件、输入参数、输出参数、算法框架、AS描述及方法、如何确定系统状态和单元转移状态等问题。该仿真算法可以对多状态PMS系统可靠性等多种参数进行计算，且所需输入参数较少，编程实现简单，对任务阶段系统可靠性关系具有良好的描述能力，具有很强的通用性与实用性，很好地解决了任务阶段系统结构描述、确定系统状态及单元转移状态的技术难题。当然，本文未对温储备、其他类型表决系统进行深入研究，也没有考虑备件转换可靠性、多种失效模式、更多的单元状态等问题，这也是后续研究需要进一步完善的地方。

References)

[1] Esary J D, Ziehms H. Reliability analysis of phased missions[R]. Monterey, CA, US: Naval Postgraduate School, 1975.

[2] Kim K, Park K S. Phased-mission system reliability under Markov environment [J]. IEEE Transactions on Reliability, 1994, 42(3): 301-309.

[3] Xing L, Levitin G. BDD-based reliability evaluation of phased-mission systems with internal/external common-cause failures [J]. Reliability Engineering & System Safety, 2013, 112(1): 145-153.

[4] 聂成龙, 张柳, 于永利，等. 多阶段任务系统任务持续能力仿真模型研究[J]. 系统仿真学报, 2008, 20(3): 729-732. NIE Cheng-long, ZHANG Liu, YU Yong-li, et al. Research to PMS mission sustainability simulating models[J].Journal of System Simulation, 2008, 20(3): 729-732.(in Chinese)

[5] Murphy K E, Carter C M, Malerich A W. Reliability analysis of phased-mission systems: a correct approach[C]∥Annual Relia-

bility and Maintainability Symposium. Orlando, FL, US: IEEE, 2007: 7-12.

[6] 杨建军, 杨晶, 刘锋, 等. 基于Extend的多态PMS仿真模型[J]. 计算机工程, 2010, 36(14): 230-232. YANG Jian-jun, YANG Jing, LIU Feng, et al. Multi-mode PMS simulation model based on Extend[J]. Computer Engineering,2010, 36(14): 230-232. (in Chinese)

[7] 杨春辉, 杨建军, 姚路. 多阶段任务系统通用可靠性仿真模型[J]. 北京航空航天大学学报, 2011, 37(12): 1562-1568. YANG Chun-hui, YANG Jian-jun, YAO Lu. General model for PMS reliability[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12): 1562-1568. (in Chinese)

[8] 闫华, 王魁, 刘子林, 等.基于Markov方法的多阶段任务系统可靠性分析综述[J].兵器装备工程学报, 2016, 37(6): 92-96. YAN Hua, WANG Kui, LIU Zi-lin, et al. Reliability analysis of phased-mission system using Markov approach[J].Journal of Ordnance Equipment Engineering, 2016, 37(6): 92-96. (in Chinese)

[9] Lin J,Donaghey C. A Monte Carlo simulation to determine minimal cut sets and system reliability [C]∥Proceedings of Annual Reliability and Maintainability Symposium. Atlanta, GA, US:IEEE,1993: 246-249.

[10] 吕学志, 于永利, 刘长江. 基于Stateflow的复杂可修系统的建模与仿真方法[J]. 指挥控制与仿真. 2009, 31(6): 71-75. LYU Xue-zhi, YU Yong-li, LIU Chang-jiang. A modeling and simulation approach of complex repairable system based on stateflow[J]. Command Control & Simulation, 2009, 31(6): 71-75. (in Chinese)

[11] 杨建军, 刘锋, 黎放. 多阶段任务多态系统可靠性建模与仿真[J]. 火力与指挥控制. 2011, 36(2): 89-92. YANG Jian-jun, LIU Feng, LI Fang. Reliability modeling and simulation for phased mission system with multi-mode failures[J]. Fire Control & Command Control, 2011, 36(2): 89-92. (in Chinese)

[12] The MathWorks Inc. Stateflow getting started guide: revised for version 7.3[M]. Natick, US: The MathWorks Inc, 2009.

[13] 毛炳祥, 白桦, 程文鑫.系统战备完好性分析、计算与检测[M]. 北京:国防工业出版社, 2012. MAO Bing-xiang, BAI Hua, CHENG Wen-xin. System operational readiness analysis, computation and detection [M]. Beijing: National Defense Industry Press, 2012. ( in Chinese)

[14] Law A,Kelton D. Simulation modeling & analysis[M]. New York: McGraw-Hill, 2000.

[15] 周大庆.实用数据结构教程:Java语言描述[M]. 北京：人民邮电出版社，2007. ZHOU Da-qing. Data structure practical course for Java[M]. Beijing: Posts & Telecom Press, 2007. (in Chinese)

Reliability Analysis of Phased-mission System with Multiple States Based on Discrete Event Simulation

SU Xu-jun1, LYU Xue-zhi2

(1.Artillery Department, Ordnance Engineering College, Shijiazhuang 050003, Heibei, China；2.Simulation Training Center, Artillery Training Base of the Army, Xuanhua 075100, Hebei, China)

An algorithm of phased-mission system with multiple states is presented. The concepts of phased-mission system and its features are discussed, and an active standby (AS) tree structure method is proposed to depict the system structure of each phase. The behaviors of phased-mission system with multiple states are discussed based on state chart. According to discrete event simulation concept,a simulation algorithm is presented to estimate the reliability parameters of phased-mission system with multiple states. A case-study is introduced to verify the algorithm. The proposed simulation algorithm is very practical and versatile. The algorithm can be used to describe the complex behaviors of phased-mission system flexibly and obtain the more reliability parameters to understand the system operation.

system assessment and feasibility analysis; reliability; phased-mission system; discrete event simulation

2016-09-08

军内装备科研项目(012016012600B12507)

苏续军(1977—)，男，讲师，硕士。E-mail:sxj_china@163.com

吕学志(1979—)，男，副教授。E-mail:ghostsheep@tom.com

TP391.92

A

1000-1093(2017)04-0776-09

10.3969/j.issn.1000-1093.2017.04.020