随机共因失效条件下的多阶段任务成功概率评估研究

曹文斌， 胡起伟， 苏续军， 赵建民

(1.军械工程学院 装备指挥与管理系, 河北 石家庄 050003; 2.军械工程学院 火炮工程系, 河北 石家庄 050003)



随机共因失效条件下的多阶段任务成功概率评估研究

曹文斌1， 胡起伟1， 苏续军2， 赵建民1

(1.军械工程学院 装备指挥与管理系, 河北 石家庄 050003; 2.军械工程学院 火炮工程系, 河北 石家庄 050003)

共因失效广泛存在于装备作战任务过程中，合理地对共因失效事件进行建模，对于准确评估装备任务成功概率，具有十分重要的意义。针对现有的多阶段任务成功概率评估模型中没有考虑的一类随机共因失效问题，采用隐式二元决策图法，建立了当共因失效事件的产生服从随机分布时的多阶段任务成功概率评估解析模型，并以某型火箭炮装备为实际案例对模型进行了验证。研究结果表明：所建立的数学模型可以解决随机共因失效条件下的多阶段任务成功概率评估问题，为评估装备多阶段任务成功概率提供了模型支撑；合理地任务剖面分析与建模有助于准确评估装备任务成功概率。

系统评估与可行性分析；多阶段任务； 成功概率； 随机共因失效； 二元决策图

0 引言

多阶段任务系统(PMS)是指由执行时间上具有连续性和不重叠性，功能上具有相关性的多个阶段组成任务的复杂系统[1]。每个任务阶段，系统工作部件及结构关系、外部环境、任务要求可能不同[2]。典型的PMS有飞机[2-3]、卫星系统[4]、核电站[5]、某些武器装备[6-7]等。任务成功概率是指在规定的条件下和规定的任务剖面内，装备能完成规定任务的概率[8]。虽然研究多阶段任务成功概率评估的文献相对较多[9-14]，但是如何考虑作战任务的复杂性和装备战场损伤的不确定性，对装备多阶段任务成功概率进行评估，现有的解析模型还不能有效解决。

在战场条件下，影响装备任务成功概率的损伤可分为非战斗损伤和战斗损伤两部分。非战斗损伤主要是由自然故障、人为差错、装备不适于作战环境等原因造成的[15]，而战斗损伤是指敌方武器作用造成的装备损伤[15]。战斗损伤的产生往往具有随机性和并发性，即装备执行任务过程中，敌方武器作用的时刻、次数都是随机的，且往往会以一定的概率造成我方装备多部件同时损伤。因此，敌方武器作用是一种典型的共因失效事件，这里将这类具有随机性的共因失效称为随机共因失效(RCCF)。虽然现有的考虑共因失效的多阶段任务成功概率评估方法可以用于评估装备多阶段任务的成功概率，但是，大部分数学模型假设共因失效事件会以一定的概率发生，且发生时必然造成多个部件的同时故障(即共因失效发生的条件下部件故障概率为1)，这类共因失效被称为确定性共因失效(DCCF)。只有Wang等[16]研究了概率性共因失效(PCCF)条件下多阶段任务成功概率评估问题，即共因失效事件以一定的概率发生且以一定的概率造成多部件同时故障。但是，该模型假设共因失效事件只有发生和不发生两种情况，不适用于评估装备这类RCCF情况下的多阶段任务的成功概率。鉴于此，本文结合装备作战任务特点，考虑共因失效事件的产生服从某一分布这类随机情况，研究建立装备多阶段任务成功概率评估解析模型，并以某型火箭炮装备为例进行应用验证，从而为评估RCCF条件下装备多阶段任务成功概率提供模型支撑。

1 问题描述

装备作战环境复杂、损伤原因多、战斗损伤随机性强，为了针对性地开展研究，这里做如下假设：

1)假设装备损伤只包含战斗损伤和自然故障两部分，且战斗损伤和自然故障二者相互独立；

2)敌方武器作用的时刻服从某一分布，且以一定的概率造成我方装备多个部件同时损伤；

3)装备任务由多个阶段组成，每个任务阶段内工作的部件不同，且各任务阶段的持续时间确定且已知；

4)在任务过程中，不考虑装备维修过程。

考虑以上情况，这里以某型火箭炮装备为例，分析需要解决的问题。某型火箭炮装备的典型任务过程如图1所示，包括装填、行军、射击准备、发射、撤收和阵地转移6个任务阶段，每个任务阶段工作的部件不同，任务持续时间也不同。火箭炮装备在执行任务过程中可能存在敌方武器作用(即RCCF事件)，且到达时刻服从某一分布，并以一定概率造成火箭炮装备多部件同时损伤。决策者需要根据火箭炮装备多阶段任务特性，考虑战斗损伤和自然故障，计算火箭炮装备作战任务成功概率。在下文描述中，用“RCCF事件”代替“敌方武器作用”。

2 基于隐式二元决策图法的装备多阶段任务成功概率评估

现有的多阶段任务成功概率评估方法主要可以分为两大类：解析法和仿真法[17]。解析法包括组合建模法(如微部件法、故障树法、二元决策图(BDD)法等)、状态空间建模法(如马尔可夫链法、Petri网法等)和模块化建模法(如BDD与马尔可夫链相结合的方法等)。仿真法可以有效解决复杂情况下的任务成功概率评估问题，但是该方法计算过程较复杂，运算时间较长；而解析法的优势在于计算过程简单，计算效率高，因此这里采用解析法。BDD法是一种有效的静态建模法，广泛应用于多阶段任务成功概率评估。当考虑共因失效时，基于BDD的多阶段任务成功概率建模方法可以分为两类：显式法[18]和隐式法[16]。由于RCCF事件的发生次数是随机的，用显式法建模较困难，而且相比于显式法，隐式法建模和计算过程较简单，因此，这里采用隐式BDD法。

2.1 基于隐式BDD法的装备多阶段任务成功概率评估流程

采用隐式BDD法，对RCCF条件下装备多阶段任务成功概率评估建模的流程[16]为：

1)按照“任务阶段—功能—部件”的对应关系，进行任务剖面分析及装备结构分解。

在多阶段任务成功概率建模中，最重要的是准确分析每个任务阶段内装备各部件的工作情况及对应的结构。由于装备组成部件较多，在结构分解时，如果将其分解到最底层的组成部件，则会显著提高分析工作的复杂性。为了简化分析过程，提高分析效率，在进行“任务阶段—功能—部件”分析时，应遵循以下3个原则：

①将装备分解到实现任务阶段内某项功能的部件，其下一层次的组成部件不再细分；

②若某几个部件同时参与完成所有阶段的任务，且在各任务阶段的结构关系相同，在分析时可以将它们看作一个虚拟部件进行分析；

③重点分析易发生损伤的部件，对于不容易发生损伤的部件，可认为其任务成功概率为1，分析时将其忽略。

2)根据多阶段任务剖面分析得到的“任务阶段—功能—部件”对应关系，画出每个任务阶段的可靠性框图和故障树模型。

3)根据故障树模型，画出每个任务阶段的BDD模型。将故障树中各事件根据按向前阶段相关性(即事件排序与任务阶段顺序相同)或者向后阶段相关性(即事件排序与任务阶段顺序相反)进行排序。用ite(If-Then-Else)结构，将故障树转换为逻辑表达式为

ite(A,B,C)=AB+A′C,

(1)

即，若A成立，则B成立，否则，C成立。按照(2)式的规则，可得到各任务阶段的BDD模型。

(2)

式中：k1和k2分别表示不同部件；G=ite(k1,Gk1=1,Gk1=0)和F=ite(k2,Fk2=1,Fk2=0)为ite结构的逻辑表达式；Gk1=1=G1和Fk2=1=F1分别为部件k1和k2的状态取1时G和F的逻辑表达式；Gk1=0=G2和Fk2=0=F2分别为部件k1和k2的状态取0时G和F的逻辑表达式；◇表示“与”或者“或”逻辑运算符；index(k1)和index(k2)分别表示预先定义的部件k1和k2的事件序号。

4)根据(2)式和(3)式的规则，用逻辑“或”将各任务阶段的BDD模型连接，形成整个多阶段任务的BDD模型。对于不同部件按(2)式的规则运算，对于相同部件但不同的任务阶段(表示为kw1和kw2)，按照(3)式的规则运算。

(3)

式中：kw1和kw2分别表示相同的部件k在不同的任务阶段w1和w2；Gkw1=1=G1和Fkw2=1=F1分别为kw1和kw2的状态取1时G和F的逻辑表达式；Gkw1=0=G2和Fkw2=0=F2分别为kw1和kw2的状态取0时G和F的逻辑表达式。

2.2 仅考虑自然故障的装备多阶段任务成功概率评估

假设T=[t(1),…,t(w),…,t(W)]表示各任务阶段的持续时间长度，Dk=[dk(1),…,dk(w),…,dk(W)]表示部件k在各阶段的工作情况，则dk(w)为

(4)

若用pk(w)表示部件k在第w个任务阶段开始时未发生故障的条件下，在结束时仍未发生故障的概率。当仅考虑自然故障时，部件k在任务阶段w(w=1,2,…,W)的任务成功概率可以描述为

(5)

式中：Rko(w)表示仅考虑自然故障时，部件k在任务阶段w的任务成功概率。根据第1节中假设条件4，当不考虑装备任务中的维修过程时，部件k在任务阶段wk结束时的任务成功概率为部件k从任务阶段1到任务阶段wk各任务阶段任务成功概率之积。即

(6)

(7)

仅考虑自然故障时的多阶段任务成功概率为

(8)

2.3 考虑RCCF的装备多阶段任务成功概率评估

为了不失一般性，假设当在某个任务阶段发生RCCF事件时，装备所有组成部件(包括不参与该阶段任务的部件)都可能发生损伤。若用C=[c(1),…,c(w),…,c(W)]表示各任务阶段内是否发生RCCF事件，则c(w)可定义为

(9)

若用ti(i=1,2,…)表示第i次RCCF事件与第i-1次RCCF事件的时间间隔，ti(i=1,2,…)独立同分布，分布函数表示为F(ti). 基于更新过程理论，在任务阶段w内，RCCF事件的发生次数N(t(w))[19]为

N(t(w))=max{i:t1+t2+…+ti≤t(w)},

(10)

t(w)时刻内发生i次RCCF事件的概率[19]为

Pr(N(t(w))=i)=

Pr(N(t(w))≥i)-Pr(N(t(w))≥i+1)=

F(i)(t(w))-F(i+1)(t(w))，i=0,1,…,

(11)

则任务阶段w内发生i次共因失效事件且未造成部件k故障的概率为

Rkc(i)=(F(i)(t(w))-F(i+1)(t(w)))(1-pkf)i,

(12)

式中：pkf表示RCCF事件发生时部件k故障的概率。若用iw表示任务阶段w内RCCF事件可能发生的最大次数，则部件k在第w个任务阶段和整个多阶段任务的任务成功概率分别为

(13)

(14)

计算RCCF条件下，整个装备的多阶段任务成功概率时，这里分两种情况讨论：装备在连续的任务阶段内存在RCCF事件(记为情况1)和装备在非连续的任务阶段内存在RCCF事件(记为情况2)。情况1是指存在RCCF事件的几个任务阶段时连续的；情况2是指装备存在RCCF事件的任务阶段是非连续的，即在两个存在RCCF的任务阶段之间的某些任务阶段内肯定没有RCCF事件发生。很显然，这两种情况下的任务成功概率计算方法不同，这里分别进行讨论。

2.3.1 情况1：装备在连续的任务阶段内存在RCCF事件

图2 连续任务阶段内存在RCCF的任务剖面Fig.2 Mission profile of RCCF occurring in continuous phases

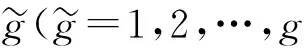
(15)

图3 任务阶段划分Fig.3 Reclassification of mission phases

(16)

(17)

(18)

(19)

将自然故障考虑在内，路径集lj对应的任务成功概率为

(20)

(21)

2.3.2 情况2：装备在非连续任务阶段内存在RCCF

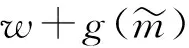
图4 任务阶段划分Fig.4 Reclassification of mission phases

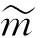
(22)

则仅考虑随机共因失效时，路径集lj的任务成功概率为

(23)

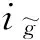
(24)

(25)

根据(21)式和(23)式，考虑路径集的相关性，可得到在非连续的任务阶段内存在随机共因失效情况下的装备多阶段任务成功概率为

(26)

3 案例分析

3.1 某型火箭炮装备多阶段任务成功概率评估

某型火箭炮装备的任务剖面如图1所示。根据2.1节的多阶段任务成功概率评估流程，对某型火箭炮装备进行“任务阶段—功能—部件”分析，共得到50个组成部件，其中15个部件可靠度较高且不易发生战损，这里将其忽略。另外，有9个部件在参与所有任务阶段内且结构关系不变，这里将其合并为一个部件分析，简化后共有27个组成部件。各任务阶段持续时间及工作部件如表1所示，仅考虑自然故障时，各部件在各任务阶段的任务成功概率如表2所示(考虑到保密问题，这里对数据进行了处理，但不影响结论)。在“发射”阶段，部件12和部件13串联后与部件14并联，其他部件在所有任务阶段中均为串联关系。假设RCCF事件到达时刻服从指数分布，分布参数为λ=0.5 h-1. 为了方便计算，假设每次RCCF事件对火箭炮装备所有组成部件造成损伤的概率相等，值为pkf=0.015.

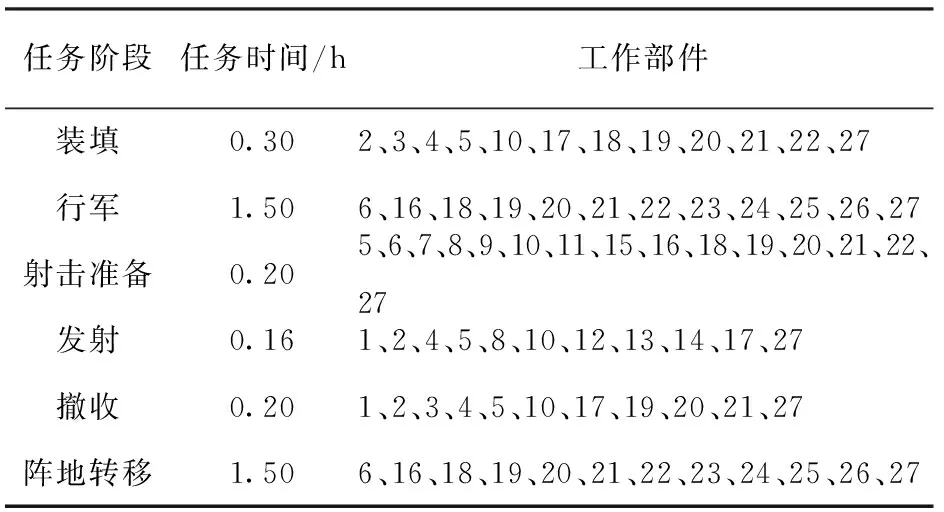
表1 各任务阶段持续时间及工作部件

根据2.1节的流程，可以得到整个多阶段任务的BDD模型，如图5所示。从图5中可以看出，共有3条任务成功时的路径集l1，l2和l3，分别为：

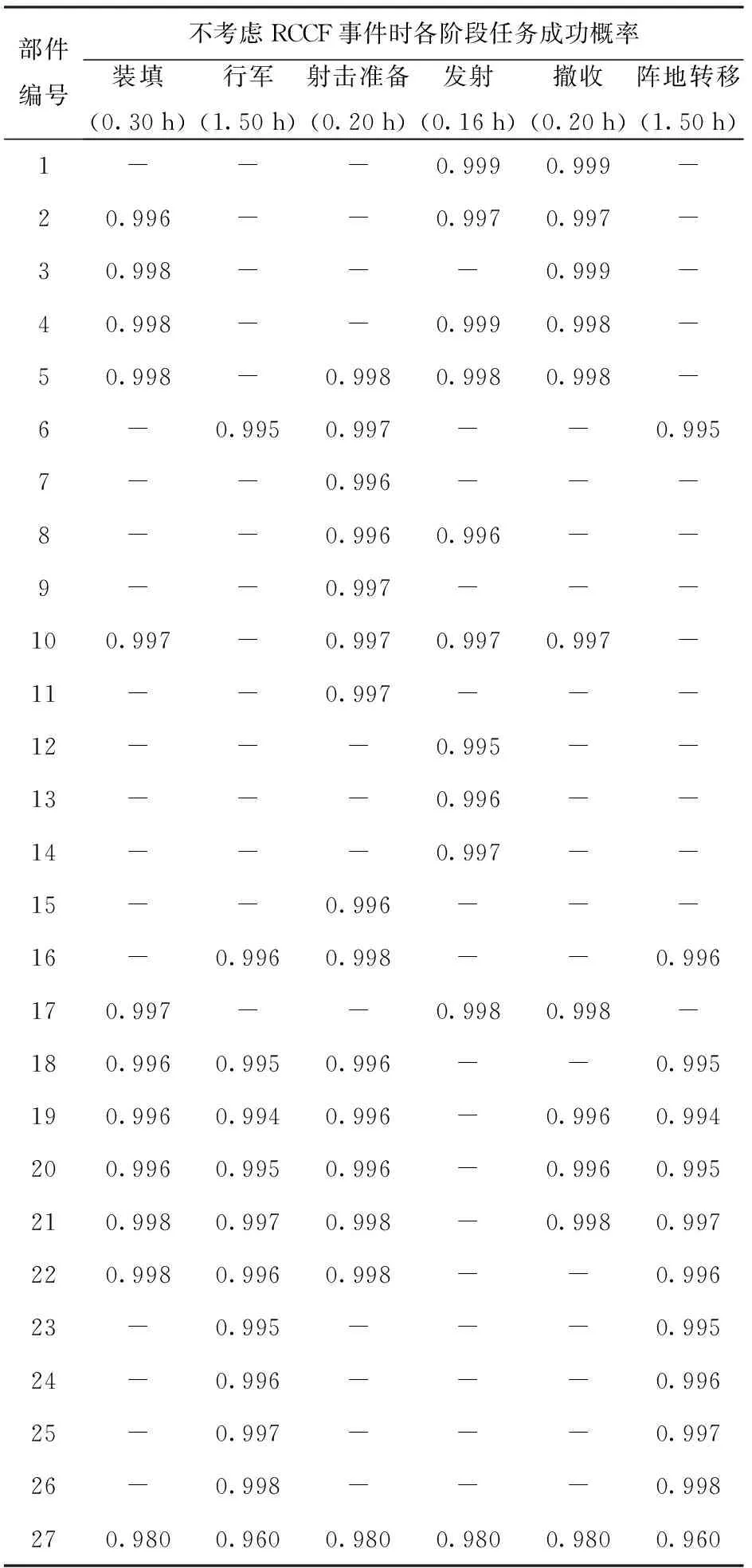
表2 仅考虑自然故障时各部件在各任务阶段的任务成功概率

注：“-”表示部件在该任务阶段未工作。

图5 多阶段任务BDD模型Fig.5 BDD model of phased mission

首先根据2.2节的模型，计算得到了仅考虑自然故障时，某型火箭炮装备多阶段任务成功概率为0.690 1. 当考虑RCCF时，这里讨论了两种情况：情况1，在任务阶段“装填”内不会发生RCCF，而在其他任务阶段都可能发生RCCF，此时，按2.3.1节的模型得到任务成功概率为0.449 2；情况2，假设在任务阶段“装填”和“发射”两个阶段内都不会发生RCCF，而在其他任务阶段内可能发生RCCF，此时，根据2.3.2节的模型得到任务成功概率为0.458 7. 通过对比可以看出，0.449 2<0.458 7<0.690 1，即不考虑RCCF时的任务成功概率最大，情况2的任务成功概率次之，情况1的任务成功概率最小，与实际情况相符。结果表明RCCF可降低任务成功概率；合理地任务剖面分析与建模有助于准确评估装备任务成功概率。

3.2RCCF事件对任务成功概率的影响分析

为了量化和评估RCCF对任务成功概率的影响，这里分析了两种情况(即情况1和情况2)下，任务成功概率R、λ和pkf之间的关系。分布参数λ决定了RCCF事件的发生次数，而pkf决定了共因失效事件发生时，造成部件损伤的概率。理论上来说，当pkf值一定时，λ值越大，任务期间发生多次共因失效事件的概率就越大，任务成功概率会越小；当λ值一定时，pkf值越大，每次共因失效事件造成部件损伤的概率越高，任务成功概率越小。因此，任务成功概率会随着λ和pkf的增大而减小。

图6 连续任务阶段内RCCF对任务成功概率的影响Fig.6 Effect of RCCF occurring in continuous phases on mission success probability

图7 非连续任务阶段内RCCF对任务成功概率的影响Fig.7 Effect of RCCF occurring in discontinuous phases on mission success probability

这里利用Matlab软件进行仿真，得到了情况1和情况2中，任务成功概率R、λ和pkf三者之间的关系，分别如图6和图7所示。从图6、图7中可以看出，在两种情况下，由本文建立的模型得到的仿真结果均与理论分析结果一致，证明了模型的正确性。另外，通过对比图6与图7的颜色和等高线，可以看出情况2的任务成功概率始终略大于情况1的任务成功概率，这是由于情况1假设在“行军、射击准备、发射、撤收和阵地转移”5个任务阶段内均会发生共因失效，而情况2假设“行军、射击准备、撤收和阵地转移”4个任务阶段内会发生共因失效，即情况1的共因失效事件发生次数要大于情况2的共因失效事件发生次数。因此，情况2的任务成功概率会大于情况1的任务成功概率。该结论与3.1节的分析结果相符，侧面说明了RCCF会降低任务成功概率。

4 结论

考虑装备在执行多阶段任务过程中可能会发生战斗损伤这一复杂情况，针对RCCF条件下多阶段任务成功概率评估问题，采用隐式BDD法，建立了当共因失效事件的产生服从随机分布时的多阶段任务成功概率评估解析模型，并以某型火箭炮装备为例进行了验证，为评估战时装备多阶段任务成功概率提供了模型支撑。模型中，装备各部件的寿命和随机共因失效事件的产生时刻可以服从任意分布。另外，可以从以下两个方面进一步深入研究：一是考虑任务持续时间服从某一分布的情况，例如某些装备执行作战任务时，火力打击时间往往是不确定的，可用某一分布进行描述；二是RCCF条件下多状态系统的多阶段任务成功概率评估有待进一步研究。这也是作者下一步将要研究的内容。

References)

[1] Xing L D, Dugan J. Analysis of generalized phased-mission systems reliability, performance and sensitivity [J]. IEEE Transactions on Reliability, 2002, 51(2): 199-211.

[2] Xing L D, Levitin G. BDD-based reliability evaluation of phased-mission systems with internal/external common-cause failures [J]. Reliability Engineering and System Safety, 2013, 112: 145-153.

[3] Xing L D. Reliability evaluation of phased-mission system reliabi-lity, performance and sensitivity [J]. IEEE Transactions on Reliability, 2007, 56(1): 58-68.

[4] 朱海鹏. 基于BDD的多阶段任务系统可靠性建模分析[D]. 成都: 电子科技大学, 2010. ZHU Hai-peng. BDD-based reliability analysis of phased-mission system [D]. Chengdu: University of Electronic Science and Technology of China, 2010. (in Chinese)

[5] Xing L D, Amari S V, Wang C N. Reliability of k-out-of-n systems with phased-mission requirements and imperfect fault coverage [J]. Reliability Engineering and System Safety, 2012, 103(3): 45-50.

[6] 张涛, 郭波, 谭跃进, 等. 一种基于BDD的多阶段任务系统可靠度新算法[J].系统工程与电子技术, 2005, 27(3): 446-448. ZHANG Tao, GUO Bo, TAN Yue-jin, et al. New BDD-based algorithm for reliability analysis of phased-mission systems[J]. System Engineering and Electronics, 2005, 27(3): 446-448. (in Chinese)

[7] 张涛, 郭波, 武小悦, 等. K阶段变化条件下k/N:G系统的备件保障度模型[J]. 兵工学报, 2006, 27(3): 485-488. ZHANG Tao, GUO Bo, WU Xiao-yue, et al. Spare availability model for k-out-of N system with different k in different phases [J]. Acta Armamentarii, 2006, 27(3): 485-488. (in Chinese)

[8] 甘茂治, 康建设, 高崎. 军用装备维修工程学[M]. 第2版. 北京: 国防工业出版社, 2005. GAN Mao-zhi, KANG Jian-she, GAO Qi. Military equipment maintenance engineering [M]. 2nd ed. Beijing: National Defense Industry Press, 2005.(in Chinese)

[9] Gregory L, Amari S V. Reliability of non-repairable phased-mission systems with common cause failures [J]. IEEE Transactions on Systems, Man and Cybernetics: Systems, 2013, 43(4):967-978.

[10] Levitin G, Xing L D, Yu S J. Optimal connecting elements allocation in linear consecutively-connected systems with phased mission and common cause failures [J]. Reliability Engineering and System Safety, 2014, 130:85-94.

[11] Wu X Y, Wu X Y. Extended object-oriented petri net model for mission reliability simulation of repairable PMS with common cause failures [J]. Reliability Engineering and System Safety, 2015, 136:109-119.

[12] Wu J M, Wu X Y, Liu Y L, et al. Reliability analysis of large phased-mission systems with repairable components based on success-state sampling [J]. Reliability Engineering and System Safety, 2015, 142:123-133.

[13] Wu J M, Wu X Y. Reliability evaluation of generalized phased-mission systems with repairable components [J]. Reliability Engineering and System Safety, 2014, 121: 136-145.

[14] Levitin G, Xing L D, Amir E Z, et al. Heterogeneous warm standby multi-phase system with variable mission time [J]. IEEE Transactions on Reliability, 2016, 65(1): 1-13.

[15] 李建平, 石全, 甘茂治. 装备战场抢修理论与应用[M].北京: 兵器工业出版社, 2000. LI Jian-ping, SHI Quan, GAN Mao-zhi. Battlefield damage repair theory and application [M]. Beijing: Publishing House of Ordnance Industry, 2000. (in Chinese)

[16] Wang C N, Xing L D, Levitin G. Probabilistic common cause failures in phased-mission system [J]. Reliability Engineering and System Safety, 2015, 144: 53-60.

[17] Xing L D, Amari S V. Reliability of phased-mission systems [M]∥Krishna B M. Handbook of Performability Engineering. London: Springer, 2008: 349-368.

[18] Fan D M, Wang Z L, Liu L L, et al. A modified GO-FLOW methodology with common cause failure based on discrete time Bayesian network [J]. Nuclear Engineering and Design, 2016, 305:476-488.

[19] 马文·劳沙德. 系统可靠性理论：模型、统计方法及应用[M]. 第2版. 北京: 国防工业出版社, 2011. Marvin R. System reliability theory: models, statistical methods, and applications[M]. 2nd ed. Beijing: National Defense Industry Press, 2011.(in Chinese)

Research on Phased-mission Success Probability Assessment under Random Common Cause Failures

CAO Wen-bin1， HU Qi-wei1， SU Xu-jun2， ZHAO Jian-min1

(1.Department of Management Engineering, Ordnance Engineering College, Shijiazhuang 050003, Hebei, China;2.Department of Artillery Engineering, Ordnance Engineering College, Shijiazhuang 050003, Hebei, China)

Common cause failure exists in the performing process of military equipment mission. The reasonable modeling of the common cause failure events is of great significance to the accurate assessment of mission success probability. A kind of random common cause failure has not been considered in the existing mission success probability assessment models for phased-mission system. The implicit BDD (binary decision diagrams) method is used to model the phased-mission success probability when the occurrence of the random common cause failure event follows a certain distribution. A real example is used to verify the validity of the proposed model. The results show that the proposed model can be used to assess the phased-mission success probability considering random common cause failure, and the reasonable modeling mission profile contributes to the accurate evaluation of mission success probability.

system assessment and feasibility; phased-mission; success probability; random common cause failure; binary decision diagram

2016-11-08

国家自然科学基金青年科学基金项目(71401173)

曹文斌(1988—), 男, 博士研究生。E-mail: wbyzq@foxmail.com

胡起伟(1979—)， 男， 副教授， 硕士生导师。 E-mail: h_q_w@sina.com

E92

A

1000-1093(2017)04-0766-10

10.3969/j.issn.1000-1093.2017.04.019