基于模糊控制的金属检测导航智能车转向系统研究
2017-04-24庞川川
庞川川
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
基于模糊控制的金属检测导航智能车转向系统研究
庞川川
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
提出了LCR检测方案作为金属检测导航智能车的道路识别方式,在此基础上,列举了小车在高速情况下通过连续急弯的三种转向方案,并实验验证了小车对于每种转向方案的动态效果。构建了自适应模糊PD控制器,以偏差和变差作为模糊输入,采用最大隶属度原则调整控制规则,进而实现了以金属检测为导航的智能车转向自适应系统设计。
金属检测;线圈排布;双路作差;偏差修正;模糊PD控制
智能车是一个集环境感知、决策规划、多等级辅助识别等功能于一体的综合系统。[1] 93-97转向系统在智能车控制系统中是非常重要的组成部分,传感器识别赛道后,送入控制器进行分析得出偏差,然后执行器响应偏差。通常在设计转向系统时,可以把该系统描述成一个关于输入参数,过程状态变量,输出参数的数学模型,[2]618-621对模型进行分析优化后可以得到最优的设置参数。
以金属检测为导航的AGV小车相对于其他导航方式具有成本低、对环境要求低、易更改路线等优点,是目前得到较多研究的导航技术之一。在金属检测传感器LDC1000采集有限数据的情况下,转向算法的设计对于小车的灵敏性和抗干拢性非常重要,文献一提出将偏差的二次项作为比例部分控制舵机偏转,[3]63-64可以提高小车的过弯性能,但是不适用于以金属检测为导航的智能车转向系统。
1 LCR金属检测方案
传统的金属检测循迹小车通常采用单路或双路线圈导航,利用线圈相对中线的偏差来控制小车方向。经实验验证,此方案主要适用于区域内自动探测和定位不同的金属物体,[4]63-66如探测硬币、扫雷等,不适用于对抗干扰性和灵敏度要求较高的竞速系统。LCR金属检测方案在原方案的基础上,加入中路线圈,三路线圈的排布遵循“干扰最少、范围最广”的原则,既要减少线圈之间的互感,又要保证小车的检测范围最大。

图1 线圈排布
该方案将赛道划分为3个区间范围:区间A:[-30°,30°],区间B:[-180°,-30°],区间C:[30°,180°]。在A区间范围内,偏转角与小车偏离中线程度呈线性响应,小车在直道不会出现“摇头”现象。在BC区间范围内,将小车偏转角置最大,小车可以顺利通过弯道。转向算法具体如下:首先通过初始标定采集赛道情况。分别标定左路位于铝膜正上方时,左路最大值、右路最小值;右路位于铝膜正上方时,左路最小值、右路最大值;两路线圈沿铝膜平行放置时,左路中值、右路中值、中路中值;以5ms控制周期对LDC1000传感器输出的数字量进行滑动平均滤波,再进行归一化处理,归一范围是0~100. sensor_to_one[i]=(float)(AD_valu[i]-min_v[i])/(float)(max_v[i]-min_v[i]);时刻记录左右两路线圈的数值,当左路线圈或右路线圈的数值小于丢线阈值时,即将丢线标志位置为True,再结合中路传感器的数值,当中路传感器数值小于偏转阈值时,可判定小车偏转角度较大,做丢线处理。根据丢线标志位将偏差置于最大,不丢线情况下,舵机根据左右线圈差值线性偏转。
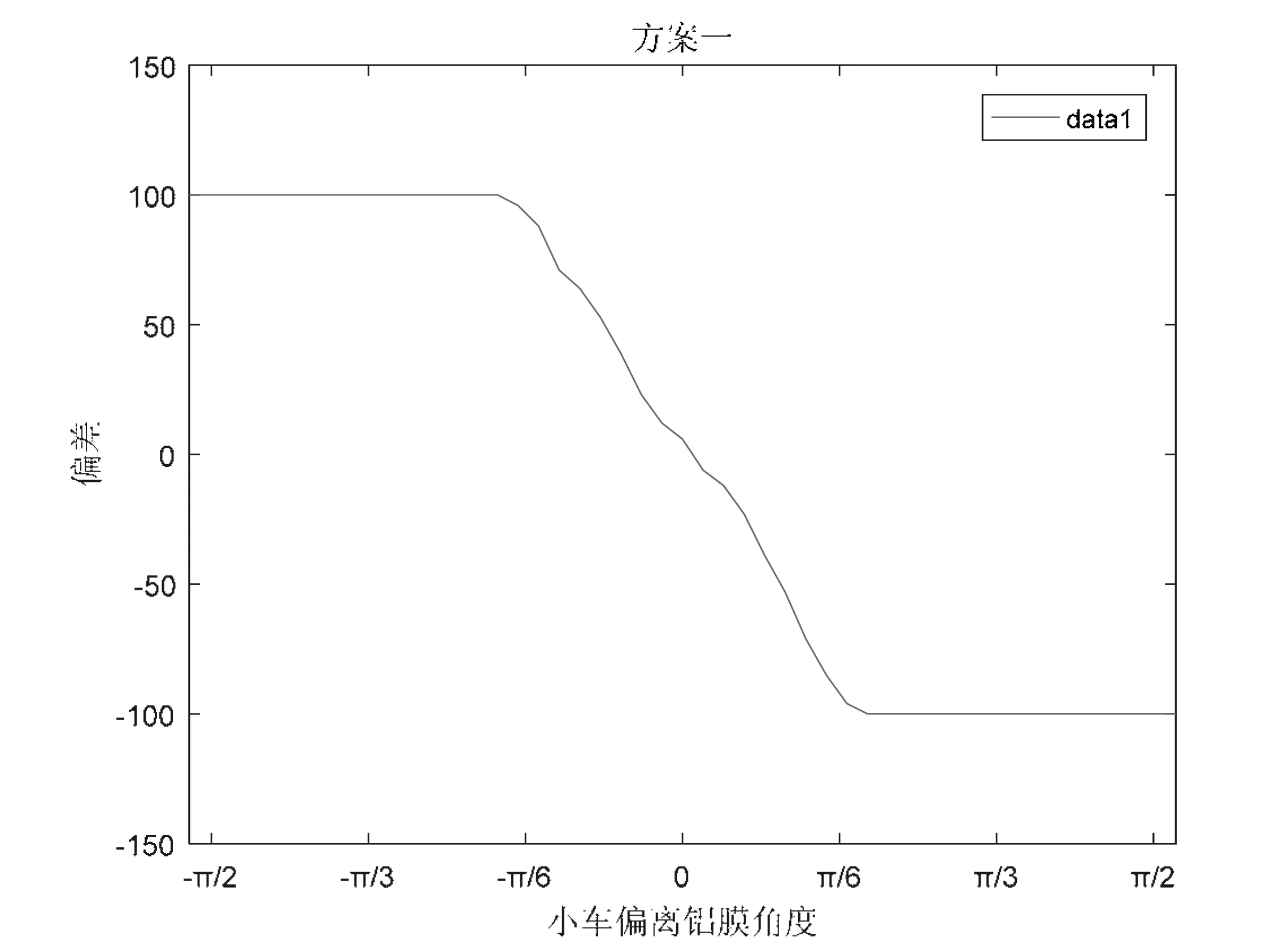
图2 方案1偏差曲线
此方案对双路线圈导航策略作了进一步的优化,低速情况下小车在直道行驶具有较好的稳定性和抗干扰性,解决了原有方案的丢线问题,但是实验发现,当小车高速通过曲率半径较大的连续急弯时,系统易出现振荡,且响应灵敏度较差。
2 检测最大值修正偏差
采用LCR导航方案,结合“中路辅助判别,双路作差”算法,小车实现了“永不丢线”。但是小车在应对连续急弯时,系统较不稳定。当小车车速较高时,应选择较远处的点求取偏差,等效于时间上提前入弯,小车利用前轮转向带来的向心力并结合小车入弯前的固有惯性达到快速转弯的目的。[5]130-134所以小车在通过连续急弯时,需提前对赛道进行预判,并用算法修正偏差曲线替代原有严重丢线的数据。
通过记录三路传感器的最大值,判断小车偏离中线的程度。当偏离中线较大时,采用曲线修正。即当误差较小的时候,输出值很小,误差变大的时候,输出值变化得很快。具体做法如下:分别读取L(左路线圈),C(中路线圈),R(右路线圈)的值,将三路线圈中的最大值记为M。
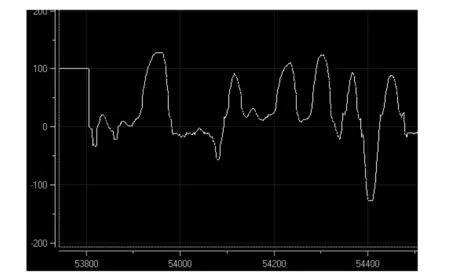
1) 当M=C时,会有以下三种情况:L>R,说明小车轻微右偏;L 2) 当M=L时,说明小车此时偏离中线较严重,右丢线。 3) 当M=R时,说明小车此时偏离中线较严重,左丢线。 图3 右丢线 图4 正常行驶 图5 左丢线 对于第1种情况,即偏差为[-60°,60°]时,系统采取线性响应,偏差为正常差值或为正常差值的倍数。第2种情况,即当偏差较大时,即可判定小车丢线较为严重,此时小车通过弯道产生较强的系统延时,对于连续的急弯道,滞后性很强。对于此种情况,将偏差根据两路线圈中的最大值,修正为一个较大值D_valueTemp,并比较此较大值与偏差的大小,一旦当D_valueTemp小于偏差时,计算出D_valueTemp与偏差的残差,当D_valueTemp减去残差小于偏差时,将偏差置成D_valueTemp减残差。即用左路或者右路的数值来拟合偏差。 chazhi=±(int16)((1/(float)(AD[1 | 2]+a))*13000-c) 此处a、c的值可根据小车的响应情况动态设定,拟合的最好状态就是将原有曲线补成一个平滑的曲线,此时在小车静止状态下对小车进行标定,其偏差曲线平滑度较好。但是实验发现,静态的偏差曲线不适用于小车动态行驶,小车实际运行较好的曲线,是当偏差较大时将其偏差置于一个极大值。偏差曲线如图所示,横坐标是传感器采集回来的赛道中心线相对于赛车中心的偏移量,纵坐标表示转角大小。 图6 方案2偏差曲线 通过检测最大值修正偏差,提高了舵机转向的灵敏性,对于弯道曲率半径较小的赛道具有较强的自适应能力,但是减弱了小车的抗干扰性,使其稳定性降低,在直道行驶中,一个微小干扰的引入即对系统造成很大的影响。 小车转向系统是一个非线性过程,用精确的数学模型对其进行描述是非常繁重的任务。所以在原有方案基础上引入模糊控制器,模糊控制将过程变量引入控制回路是静态非线性的,使得小车在转向过程中稳定性更好。 传统PID控制在直道行驶过程中,容易因超调产生振荡,且一组固定不变的PID参数无法适应变量众多,干扰众多的转向系统。[6]166-171模糊 PID控制相较于传统PID控制算法具有较好的稳定性和实时性,可以在转向时根据偏差和变差的值基于专家知识及时修改参数。由于舵机需要转向及时,积分项用来消除稳态误差,但对于系统有很强的滞后性,所以在转向系统中不引入积分项,采用模糊PD控制算法。 模糊控制器的基本结构通常由4个部分组成:模糊化接口、规则库、模糊推理、清晰化接口。[7]51-53本文通过定义量化因子将输入语言变量的论域从实际的连续域转换到离散的有限整数域。对于输出变量未使用量化因子,直接将传统PD参数的动态效果应用到该模糊控制系统中去。 该模糊控制系统输入为偏差e,变差ec,输出为kp,kd,是一个双输入输出的模糊控制系统。规范化的偏差模糊集为{NS,NM,NB,ZO,PS,PM,PB},偏差e的论域为[-3,+3],变差ec的论域为[-0.3,+0.3],kp的论域为[0,+18],kd的论域[0,+20],其中输出变量的论域由传统PD控制器大致确定,然后根据小车运行效果动态整定。 通常模糊控制的规则基于控制类型和实际经验:当偏差e较大时,需要给出正的控制量,进一步的,如果变差ec为PB,PM,其偏差为正较大且仍有加大的趋势,所以加大反向控制输出量kp设置为NB.对于其他组合也可总结出类似的规律。根据文献8,“FSW方法通过设定值权系数方法上改进的模糊逻辑调整权系数法,具有很好的跟踪设定值,减少符合扰动的性能,能实现最优整定”。[8]325-328最终规则表如下所示: Rulei:If e is Ai and ecis Bi then kp=f1(Ai,Bi)and kd=f2(Ai,Bi); i=1,2,3,…,n 表1 模糊规则表 表2 模糊规则表 该模糊控制器隶属度函数两侧为梯形隶属函数,中间为三角形隶属函数。一般来讲隶属函数的选择对控制效果影响不大,主要的影响因素是每个模糊子集的宽度选择。[9]10-14 图7 规则的三维曲面显示 采用最大隶属度原则,将推理得到的模糊子集转换为精确值,以得到最终的舵机偏转角度的论域先在PD算法控制下得出一个较为优化的区间范围,实际参数的设置还要根据小车的实际情况和赛道的摩擦力大小确定。 实验赛道全长为17.5m,采用宽度为50cm的PVC耐磨塑胶地板材料制作,赛道元素为小s弯道、大s弯道、连续急弯等元素。感应金属使用宽度5cm、厚度0.1cm的铝膜,两道铝膜铺设在赛道中央,间距为0.5cm。测试小车为飞思卡尔大学生竞赛车模-模型车A,其尺寸为27*16*8cm,有较好的调零装置,可自由组装。[10]45-49舵机采用S3010型号通用伺服器,当供电为6.0V时,其动作速度为0.16+0.02[sec/60度],反应速度快,转向灵敏。 实验分别比较了采用三种转向方案下的实验数据,用蓝牙对数据进行采集观察小车的运动状态,用秒表记录小车在三种开环占空比Ⅰ=%17,Ⅱ=%30,Ⅲ=%50控制等级下所用的时间,每种等级试验12次,计算其速度,并求其均值和方差。在试验过程中,由于环境变量相同(赛道状态、外部干扰),所以可不计入系统比较。 表3 三种方案的均值和方差 比较三种方案的速度均值显示,方案三相较于其他两种方案,在相同开环占空比下,小车的速度更快;在低速情况下,方案一小车稳定性最好,高速情况下,方案三小车稳定性最好。总的来说,模糊控制对于以金属检测为导航的智能车的转向有较好的效果。如图为采用方案三速度等级为III时,用蓝牙记录小车运行时的偏差曲线图,曲线平滑度较好,说明小车队赛道的自适应性较强,转弯效果较好。 图8 小车运动偏差曲线 本文分析了三种不同的转向控制方案,比较了各种算法的优缺点,将以金属检测为导航的智能车从普通转向策略转变到模糊PD控制算法,通过实验验证了模糊控制对于复杂转向系统的优越性。但是由于此实验三个速度等级均是开环占空比,速度环未采用闭环控制,没有将方向环与速度环进行很好地融合,所以还需要进一步的实验研究。 [1]王荣本,李冰,等.世界智能车辆研究概述[J].公路交通科技,2001,18(5): . [2]潘阳,冯能莲,等.电动助力转向系统模型预测控制策略的研究[C].2015年中国汽车工程学会年会论文集,2015. [3]张明琦,余善恩,刘国华.二次函数PD算法在智能转向车中的应用[J].哈尔滨师范大学自然科学学报,2015,31(03). [4]李艳红,李自成,孙仕琪.基于STM32单片机的金属物体探测定位器系统的设计与实现[J].仪器技术与传感器,2016(4). [5]魏玉虎,石琛宇,姜建钊,常华.基于视觉的智能车转向控制策略[J].电子技术应用,2009(1). [6]王述彦,师宇,冯忠绪.基于模糊PID控制器的控制方法研究[J].机械科学与技术,2001:30(1). [7]刘素芹,刘新平,等.PID与模糊控制算法的比较及其改进[J].控制工程,2003:10(1) . [8]宋筱玲,潘学军.模糊规则调整微分作用的PID控制方法[J].仪器仪表学报,2004,25(3). [9]窦国伟,马海涛,马先萌.基于模糊控制算法的增量式电动车能量分配策略[J].新能源汽车,2012(3). [10]朱昌平,李永强,单鸣雷.飞思卡尔智能车常见技术问题与解决方案[J].实验室研究与探索,2012(04). Class No.:TP273 Document Mark:A (责任编辑:蔡雪岚) steering system based on fuzzy control of Metal detection car Pang Chuanchuan (Anhui University of Finance and Economics, Bengbu, Anhui 233030,China) The LCR scheme is proposed as the method of road identification for the detection of intelligent car, On this basis, three high speed of steering schemes are listed, .And using experiment verified the dynamic effect of each way The adaptive fuzzy PD controller is constructed, With the deviation and variation as the fuzzy input, the control rule is adjusted by the maximum membership principle. It is achieved by metal detection for the navigation of Adaptive steering system. Metal detection; Coil configuration; Two-way difference; Deviation correction; Fuzzy PD 庞川川,安徽财经大学电子信息工程系本科学生。研究方向:嵌入式系统与应用。 2016年国家级大学生创新创业训练项目(编号:201610378119)。 1672-6758(2017)04-0075-5 TP273 A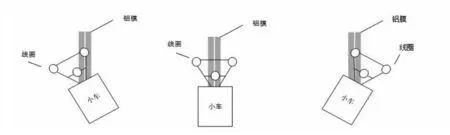

3 模糊PD控制



4 实验结果与分析

结语
