飞机受损件打磨表面形状对激光喷丸残余应力的影响*

徐晓 帅高鹏 程秀全 夏琴香†

(1.华南理工大学 机械与汽车工程学院， 广东 广州 510640;2.广州民航职业技术学院 飞机维修工程学院， 广东 广州 510403)

飞机在服役过程中，其结构件在恶劣工作环境下极易出现腐蚀损伤[1- 3].在对腐蚀损伤区域进行修复前，首先需要对该区域进行打磨，打磨后材料表面的过渡区域会产生诸如平面、凹圆弧面、凸圆弧面、双凸面、双凹面和凸凹面等表面形状[4].目前国内外学者在研究曲面上激光喷丸问题时，常将曲面激光喷丸简化为平面激光喷丸，这种简化方法对于曲率较小的曲面往往能够得到接近真实的模拟结果，但对于曲率较大的曲面，由于该区域极易成为应力集中危险区域[5- 6]，采用上述简化方法将会带来较大偏差，难以准确预测材料表面残余应力分布状况.研究不同表面形状及曲面曲率对材料表层残余应力分布的影响规律对于激光喷丸在飞机维修中的应用具有极其重要的意义.

Vasu等[7- 8]通过对飞机吊耳的激光喷丸研究发现，激光喷丸后，材料表面残余应力由大到小排列依次为凹圆弧面、平面、凸圆弧面，但其未对双凸面、双凹面等表面形状下的残余应力进行分析，因而无法直接利用其所获结论预测飞机受损件激光喷丸修复后残余应力分布状况.盛湘飞[9]基于飞机受损件常用材料7075铝合金，利用传统机械喷丸工艺，对不同表面形状下材料表面残余应力进行分析，发现材料表面残余压应力由大到小依次为凹圆弧面、凸凹面、双凹面、平面、凸圆弧面、双凸面，不同表面形状对材料内部残余压应力层深度影响不大.

文中基于飞机受损件常用材料7075-T6铝合金，通过对打磨后表面形状进行分析，采用函数对不同表面形状进行表征，研究不同表面形状及曲面曲率下材料表面的残余应力分布，为更好地掌握打磨后受损件表面复杂形状下的残余应力分布规律奠定基础.

1 飞机受损件打磨区域表面形状分类

表1 不同表面形状判定条件及其表面方程Table 1 Predicate conditions and surface region equations of different surface shapes

2 激光喷丸有限元模型

2.1 冲击波压力模型

1990年，Fabbro等[12]通过约束模型下激光喷丸试验并结合一定的理论分析，得出激光喷丸冲击波峰值压力的计算式如下：

(1)

式中，Pmax为峰值压力，ε为激光内能转化为热能系数，Z为折合声阻抗，I0为激光功率密度.

Zhang等[13]基于激光能量在空间上呈准高斯分布，提出冲击波压力在空间上亦呈准高斯分布，通过对Fabbro冲击波压力计算方法进一步改善，得出冲击波压力随空间分布的计算式如下：

(2)

式中，x、y为冲击区域某点的坐标值，R为光斑半径.根据式(2)，采用归一化处理，利用Matlab绘制冲击波压力空间分布图，如图1所示.

图1 冲击波压力空间分布Fig.1 Distribution of shock wave pressure

2.2 网格划分及边界条件

数值分析模拟结果的准确性与网格的划分紧密关联[14].由于激光喷丸过程极其短暂(ns级)，金属材料的动态响应十分剧烈，因而其对网格的要求远远高于常规有限元模拟[15].不同表面形状下激光喷丸有限元模型均采用相似的网格划分原则，下面以平面状态下激光喷丸有限元模型网格划分方法进行说明(其他形状与之相似)，其网格划分如图2所示.

图2 网格划分与边界条件示意图

Fig.2 Schematic diagram of grid partition and boundary conditions

胡永祥[16]通过对45钢和LY12铝合金的激光喷丸研究提出，在激光喷丸过程中，应力波主要沿纵向z传播，因而在划分网格时，纵向应采用更加紧密的网格进行划分.划分后的单元在x、y、z方向的尺寸分别用lx、ly、lz表示.横向上，对激光喷丸区域采用lx=ly=R/20进行划分；纵向上，由于激光喷丸残余应力层深度可达1 mm，为使模拟结果更加准确，对距冲击区域表面2 mm深度网格进行细化，并对细化区域采用lz=R/40进行划分.网格划分采用的单元类型为C3D8R，模型底部采用固定约束，模型的剖面设置为对称边界.7075-T6铝合金材料的性能参数如表2所示[17].

表2 7075-T6铝合金材料的性能参数Table 2 Mechanical properities of 7075-T6 aluminum alloy

3 飞机受损件打磨表面形状对残余应力分布的影响规律

3.1 表面形状对残余应力分布的影响规律

为了研究表面形状对材料表层残余应力分布的影响规律，利用三维建模软件UG分别对平面、凸凹面、凸圆弧面、凹圆弧面、双凸面、双凹面进行建模，并以IGS格式导入有限元软件ABAQUS中，对激光喷丸过程进行建模.对于不同表面形状，当C1、C2不为0时，选取|C1|=|C2|=0.2 mm-1,即表1中不同表面形状下表面方程R=5 mm.选取激光喷丸参数如下：冲击波峰值压力Pmax=1.83 GPa、光斑直径D=2 mm、激光脉宽=10 ns、冲击一次.由于不同表面形状下残余应力σx沿表面x、y方向的分布规律相似，以凹圆弧面为例，其残余应力σx沿表面x、y方向的分布如图3所示,l为距冲击区域中心的距离.

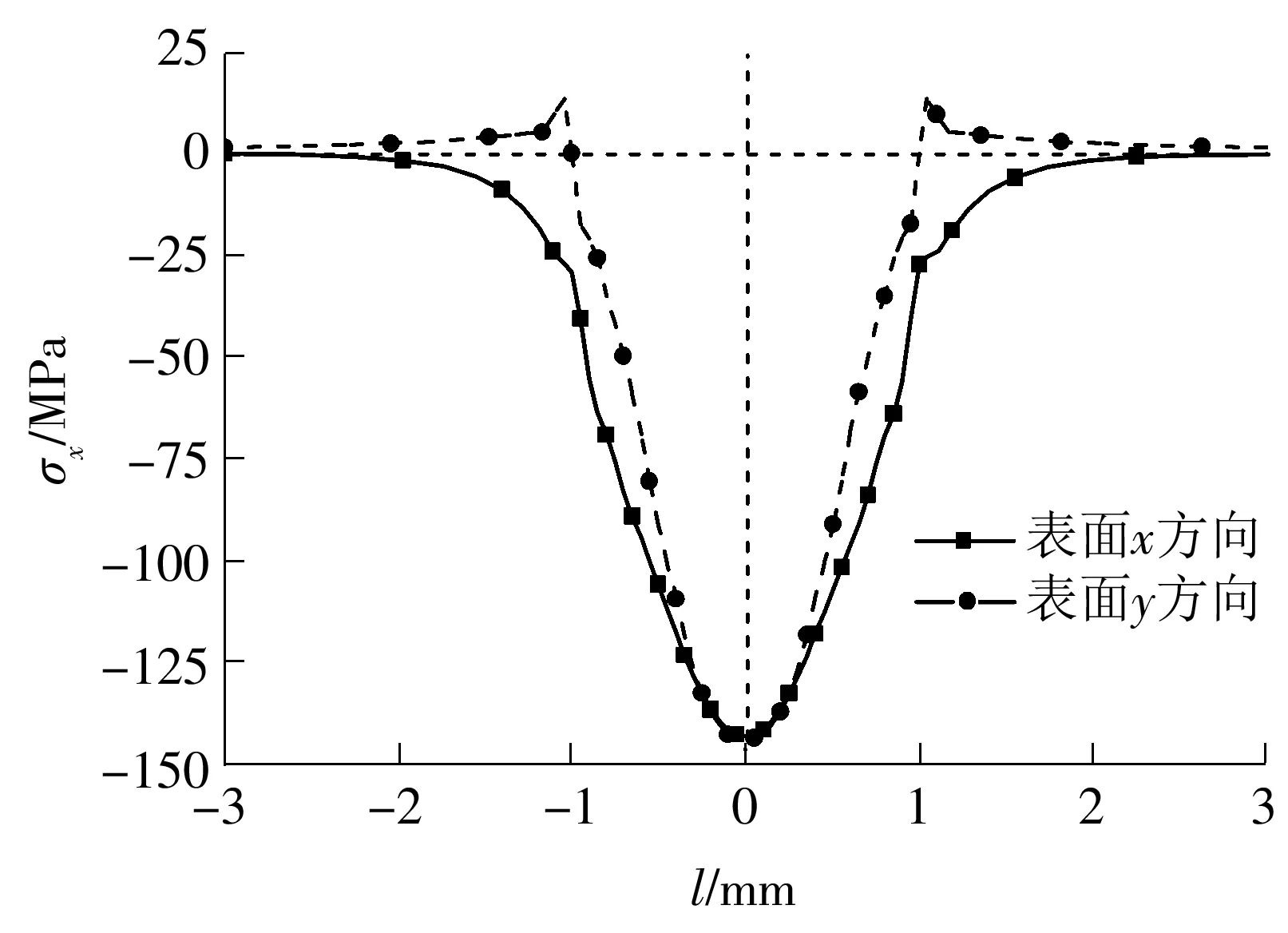
图3 凹圆弧面残余应力σx沿表面x、y方向的分布

Fig.3 Distribution of residual stressσxalongxandyaxes for concave surface

不同表面形状下残余应力σx沿深度z方向分布及表面形状与材料表层最大残余压应力σx,max关系分别如图4和5所示.

由图可知：

(1)经激光喷丸强化后，不同表面形状下材料表面最大残余压应力由大到小排列依次为：双凹面、凹圆弧面、凸凹面、平面、凸圆弧面、双凸面，表面残余压应力最大值分别为-151.6、-143.8、-140.0、-133.8、-125.5、-114.3 MPa，可由图6进行分析.

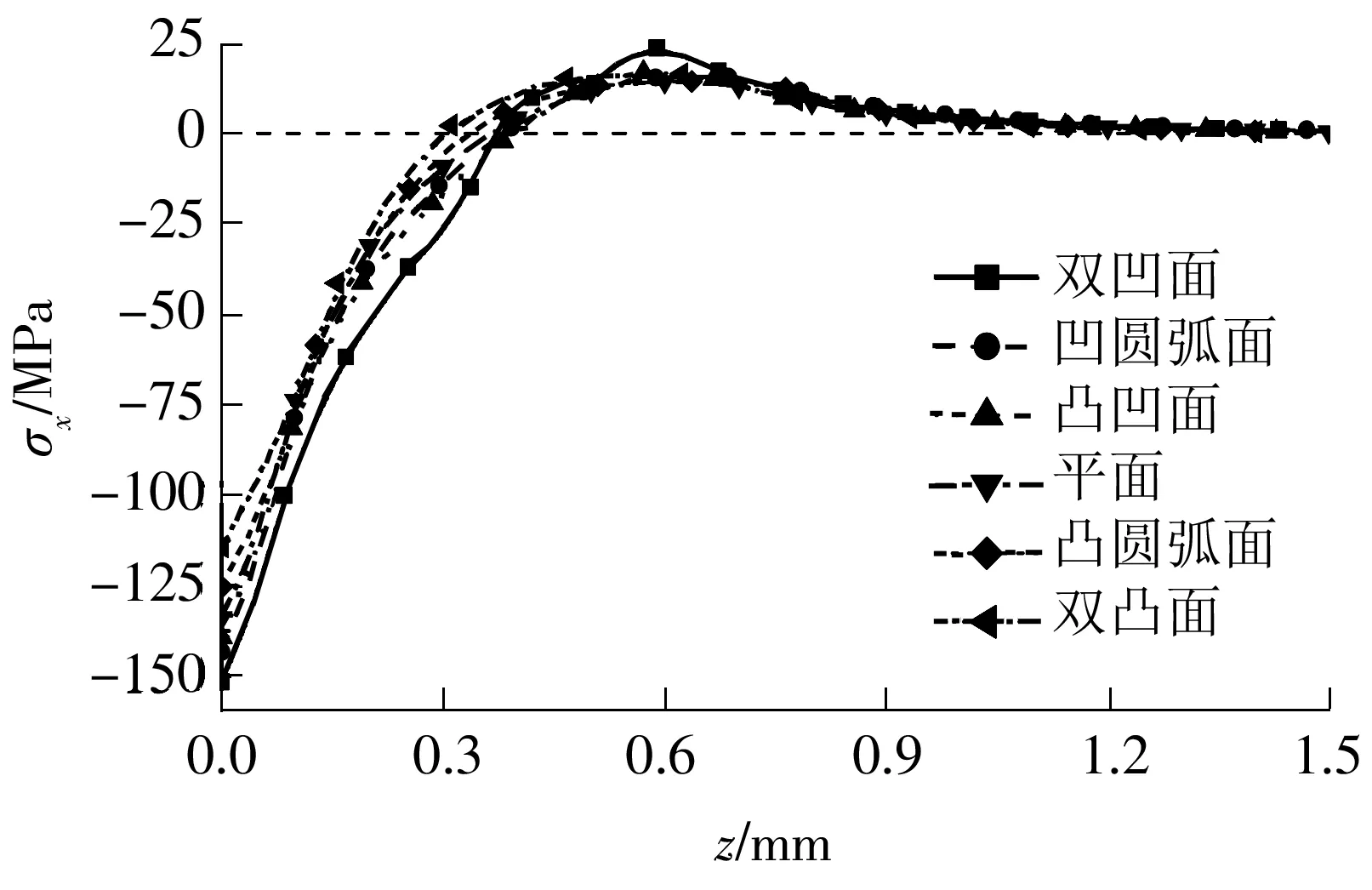
图4 不同表面形状下残余应力σx沿深度z方向的分布

Fig.4 Distribution of residual stressσxalongzaxis under different surface shapes

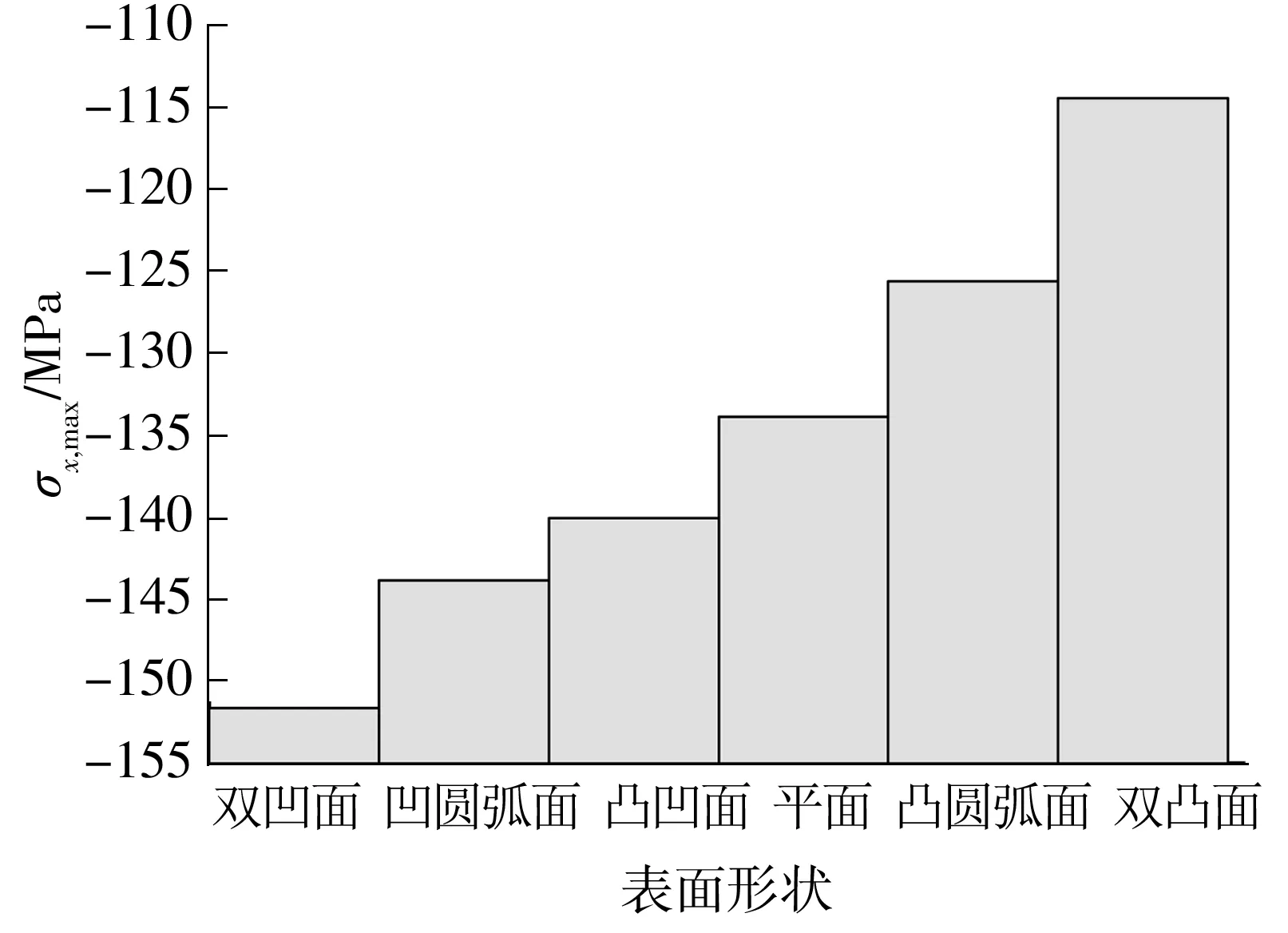
图5 表面形状与最大残余应力σx,max的关系

Fig.5 Relationship between the maximum residual stressσx,maxand surface shape

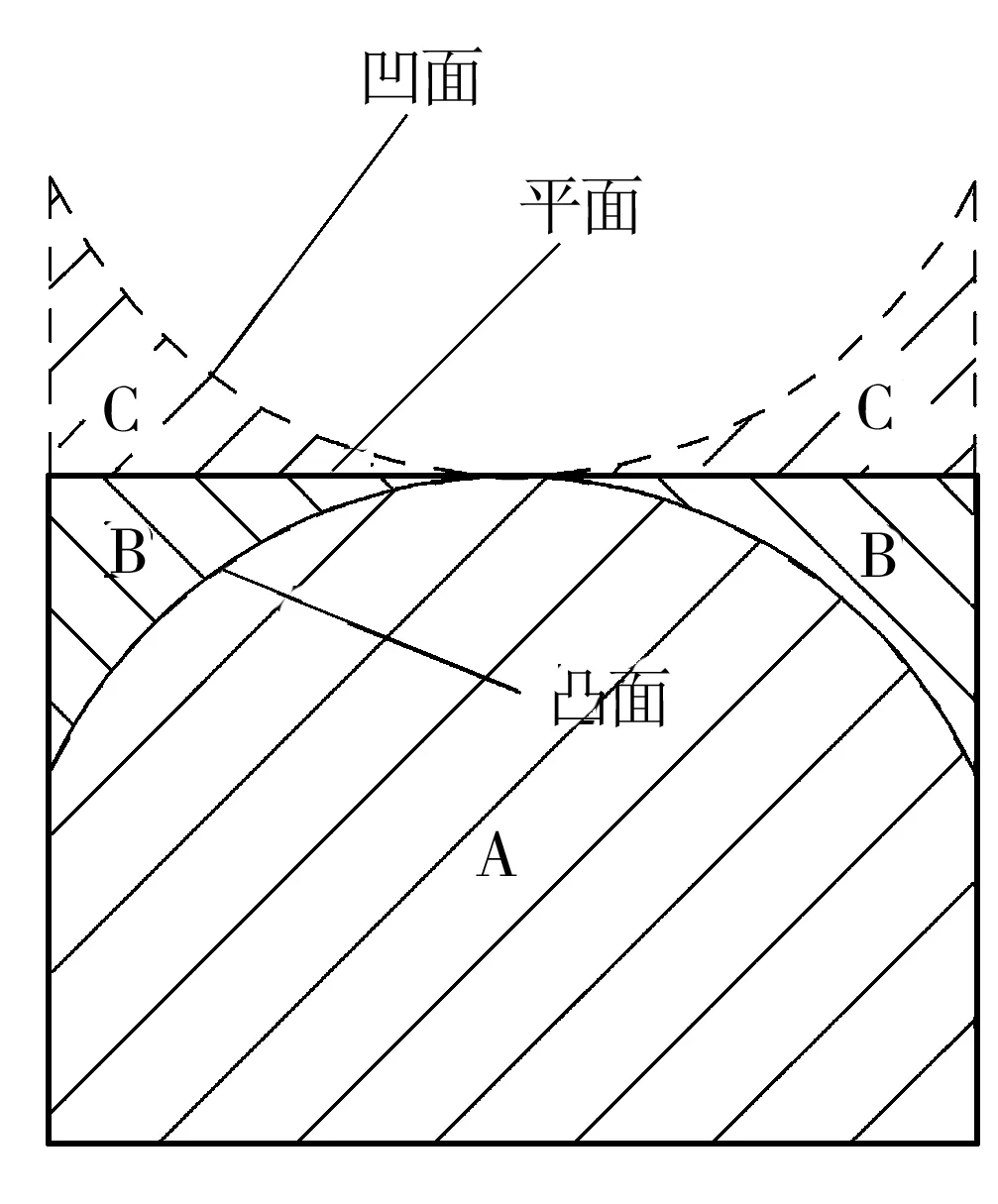
图6 不同表面形状材料的区域划分Fig.6 Partitioned regions of different surface shape

由图6可知，对不同表面形状下的材料进行区域划分，当表面形状为凸面时，模型中仅存在图中所划分的A区域材料.当表面形状为平面时，较凸面而言，增加了图中B区域材料.凹面较平面而言又增加了图中C区域的材料.在激光冲击作用时，冲击区域周围材料越多，对冲击区域的约束作用越强，冲击区域材料发生塑性变形越难，因而激光喷丸后其表面产生的残余压应力越大.

(2)不同表面形状下材料表层残余应力分布与平面状态下残余应力分布有着相似的分布规律，在表面x方向均为残余压应力，且残余压应力的大小随着距冲击区域中心的距离增大而减小，这主要是由于激光束在冲击区域中心能量密度较高，而在冲击区域边缘能量密度较低.在表面y方向，随着距冲击区域中心距离的增加，材料表面残余压应力逐渐减小，在冲击区域边缘处会出现残余拉应力，当距冲击区域中心距离进一步增加时，残余拉应力逐渐减小为0.

(3)材料内部残余压应力随着深度的加深而逐渐减小，这主要是由于冲击波在材料内部的传播是一个逐渐衰减的过程，深度越深，冲击波压力越小，因而在深度方向上残余压应力逐渐减小.不同表面形状对材料内部残余压应力层深度影响较小，材料内部残余压应力层深度的大小顺序与表面残余压应力顺序相同，但变化不大.

3.2 曲面曲率对残余应力分布的影响规律

飞机受损件在打磨过程中，由于受损件尺寸或腐蚀损伤深度限制，需要打磨出不同曲率的各类表面形状组合的过渡区域.不同曲面曲率下材料表面残余应力分布不同，因而掌握曲面曲率对残余应力分布的影响规律具有极其重要的意义.

为了研究曲面曲率对材料表面残余应力分布影响规律，以双凸面和双凹面为例，分析当曲面曲率|C1|=|C2|，且取值分别为0.01、0.10、0.20 mm-1时材料表层残余应力分布状况.选取激光喷丸参数如下：冲击波峰值压力Pmax=1.83 GPa、光斑直径D=2 mm、激光脉宽=10 ns.双凸面残余应力σx沿表面x、y方向的分布如图7所示.

不同曲面曲率下残余应力σx沿深度z方向的分布及曲面曲率与最大残余压应力的关系分别如图8、9所示.

双凹面残余应力σx沿表面x、y方向的分布如图10所示，不同曲面曲率下残余应力σx沿深度z方向的分布及曲面曲率与最大残余压应力的关系分别如图11、12所示.

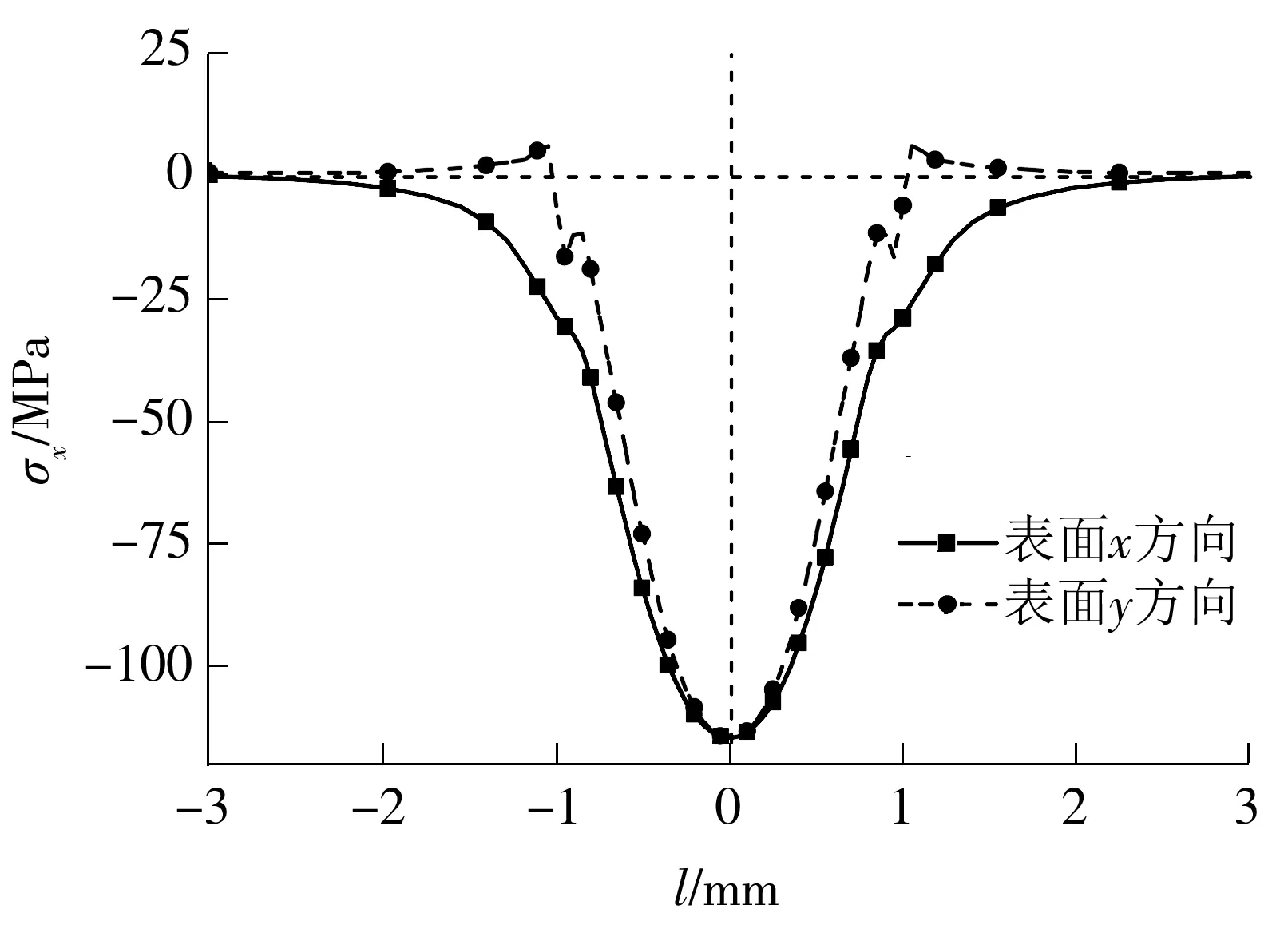
图7 双凸面残余应力σx沿表面x、y方向的分布

Fig.7 Distribution of residual stressσxalongxandyaxes for biconvex surface

图8 双凸面不同曲率下残余应力σx沿深度z方向的分布

Fig.8 Distribution of residual stressσxalongzaxis under different surface shape for biconvex surface

图9 双凸面曲面曲率与最大残余应力σx，max关系

Fig.9 The relationship between the maximum residual stressσx，maxand surface curvature for biconvex surface

由图7-12可知：

(1)随着曲面曲率的增加，双凸面表面最大残余压应力逐渐减小，双凹面表面最大残余压应力逐渐增加.这主要是由于随着曲率的增大，双凸面A区域(见图6)部分材料逐渐减少，双凹面C区域材料逐渐增加，导致在激光冲击作用时，双凸面激光冲击区域周围材料对冲击区域约束作用减弱，激光喷丸后材料表面残余压应力较小，双凹面激光冲击区域周围材料对冲击区域约束作用变强，激光喷丸后材料表面残余压应力较大.

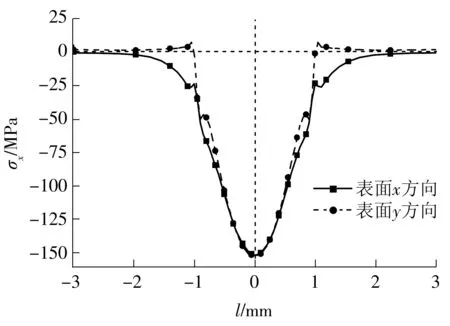
图10 双凹面残余应力σx沿表面x、y方向的分布

Fig.10 Distribution of residual stressσxalongx,yaxis for biconcave surface

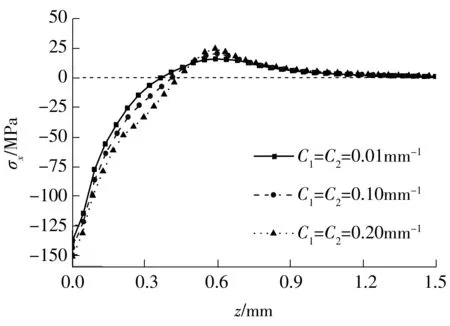
图11 双凹面不同曲率下残余应力σx沿深度z方向的分布

Fig.11 Distribution of residual stressσxalongzaxis under different surface shape for biconcave surface

图12 双凹面曲面曲率与最大残余应力σx,max关系

Fig.12 Relationship between the maximum residual stressσx,maxand surface curvature for biconcave surface

(2)不同曲面曲率对材料内部残余压应力及残余压应力层深度影响不大.

4 结论

(1)激光喷丸后，双凹面、凹圆弧面材料表面最大残余压应力较平面大；凸圆弧面、双凸面材料表面最大残余压应力较平面小，因此激光喷丸修复后，凸圆弧面、双凸面极易成为飞机受损件强度薄弱区域.

(2)凸圆弧面、双凸面材料表面最大残余压应力随着曲面曲率的增加而逐渐降低，因而在飞机受损件打磨过程中，对于凸圆弧面、双凸面应尽量采用较小的曲面曲率进行打磨.

(3)受损件表面形状及曲面曲率对材料内部残余压应力及残余压应力层深度影响较小.

(4)在飞机受损件修复过程中，改变打磨后的表面形状及曲面曲率半径难以提升残余压应力层深度，要增大残余压应力层深度，可通过改变激光喷丸参数(如冲击波峰值压力、冲击次数等)来实现.

参考文献：

[1] JONES R,MATTHEWS N,GREEN R,et al.On the potential of supersonic particle deposition to repair simulated corrosion damage [J].Engineering Fracture Mecha-nics,2015,137:26- 33.

[2] PANTELAKIS S,SETSIKA D,CHAMOS A,et al.Corrosion damage evolution of the aircraft aluminum alloy 2024 T3 [J].International Journal of Structural Integrity,2016,7(1):25- 46.

[3] OLTRA R,COLARD L,BONZOM R.A novel methodology to study localized corrosion under atmospheric simulated corrosion conditions:toward a continuous monitoring of the corrosion damage on AA2024 [J].Materials and Corrosion,2017,68(3):311- 315.

[4] 陈志超.民用飞机腐蚀损伤结构件喷丸强化方法研究 [D].广州：华南理工大学,2014.

[5] 朱有利,刘开亮,黄元林,等.应力集中和表面完整性对平尾大轴抗疲劳性能的影响 [J].机械工程学报,2012(22):93- 97.

ZHU You-li,LIU Kai-liang,HUANG Yuan-lin,et al.Effects of stress concentration and surface integrity on anti-fatigue performances of horizontal stabilizer shaft [J].Journal of Mechanical Engineering,2012(22):93- 97.

[6] VASU A,HU Y,GRANDHI R V.Differences in plasticity due to curvature in laser peened components [J].Surface and Coatings Technology,2013,235:648- 656.

[7] VASU A,GRANDHI R V.Effects of curved geometry on residual stress in laser peening [J].Surface and Coatings Technology,2013,218:71- 79.

[8] VASU A,GOBAL K,GRANDHI R V.A computational methodology for determining the optimum re-peening schedule to increase the fatigue life of laser peened aircraft components [J].International Journal of Fatigue,2015,70:395- 405.

[9] 盛湘飞.民用飞机结构件腐蚀损伤条件下喷丸强化机理研究 [D].广州：华南理工大学,2014.

[10] STEINWANDEL J,FURFARI D,OHRLOFF N,et al.Method for preventing crack formation and for slowing down the advancement of a crack in metal aircraft structures by means of laser shock rays:U.S.Patent 9,150,941 [P].2015- 10- 06.

[12] FABBRO R,FOURNIER J,BALLARD P,et al.Physical study of laser-produced plasma in confined geometry [J].Journal of Applied Physics,1990,68(2):775- 784.

[13] ZHANG W,YAO Y L.Micro scale laser shock processing of metallic components [J].Journal of Manufactu-ring Science and Engineering,2002,124(2):369- 378.

[14] DING K.Three-dimensional dynamic finite element analysis of multiple laser shock peening processes [J].Surface Engineering,2003,19(5):351- 358.

[15] 帅高鹏,徐晓,程秀全,等.激光喷丸参数对7075铝合金残余应力分布影响规律的数值分析 [J].锻压技术,2016(12):143- 149.

SHUAI Gao-peng,XU Xiao,CHENG Xiu-quan,et al.Numerical analysis on influences of laser shock peening parameters on residualstress distribution for 7075 aluminum alloy [J].Forging & Stamping Technology,2016(12):143- 149.

[16] 胡永祥.激光冲击处理工艺过程数值建模与冲击效应研究 [D].上海：上海交通大学,2008.

[17] 姜辉.激光冲击处理改善铝合金疲劳性能研究 [D].镇江：江苏大学,2010.