WPT-MSE结合PNN的电机轴承故障诊断方法
2017-04-24徐建军杜蔷楠徐建勇薛国华
徐建军,杜蔷楠,徐建勇,薛国华
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.中如建筑集团有限公司,江苏 如皋 226500)
WPT-MSE结合PNN的电机轴承故障诊断方法
徐建军1,杜蔷楠1,徐建勇2,薛国华2
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.中如建筑集团有限公司,江苏 如皋 226500)
滚动轴承是电机的重要组成零部件,在实际运行工况条件下,背景噪声干扰严重,难以实现电机轴承特征的有效提取及故障的准确判别。为了解决这一问题,提出了一种基于小波包变换(UPT)、多尺度熵(MSE)和概率神经网络(PNN)的诊断方法。首先,利用小波包变换对拾取的信号样本进行处理,并将原始信号分解为相应的子带信号分量,以减少原始信号中复杂成分之间的交叉干扰;然后,计算所得子带信号分量的多尺度熵值,并利用提取出的多尺度熵值构造能够表征电机轴承运行状态的特征向量;最后,将特征向量输入概率神经网络中,实现对电机轴承不同故障类型及损伤程度的自动识别。实测数据分析结果表明,所述诊断方法能够有效识别电机轴承的不同工作状态,从而为电机轴承的故障诊断提供了参考,具有一定的工程应用价值。
概率神经网络; 小波包变换; 多尺度熵; 电机轴承; 故障诊断
0 引言
轴承发生故障的概率约占电机全部故障的40%,因此对轴承状态进行监测、辨识是确保电机设备安全稳定运行的关键,具有重要意义[1-2]。许多非线性算法,如关联维数、近似熵、样本熵等,已被应用于诊断领域,但这些参数只能反映信号单尺度特征[3]。Costa等[4]提出的多尺度熵(multiscale entropy,MSE),可根据尺度变化反映信号在不同尺度上的特征规律。相关学者已将其用于处理机械故障信号,并得到了比样本熵更理想的效果[5-6],但信号的复杂性使得直接利用MSE描述故障特征效果欠佳。小波包变换(wavelet packet transform,WPT)可将原信号分解为相应的子带信号,从而有效减少复杂成分的交互干扰。利用该方法对原信号进行预处理,对于后续特征刻画更有利。概率神经网络(probabilistic neural network,PNN)具有良好的自学习能力及强大的并行处理能力。与BP神经网络相比,PNN网络训练过程耗时更短,结果更稳定[7]。基于上述分析,本文提出一种基于WPT-MSE和PNN的电机轴承诊断方法。
1 小波包变换
WPT是将信号在小波基函数系上展开,通过信号与小波基函数的内积运算,实现对信号的精确分解与重构。WPT同时对信号的高、低频系数进行相同形式的处理,形成了完整二叉树结构,可以将原始信号无冗余、无疏漏地映射至2j个小波包子空间(j为WPT处理层数),所得的每个子带信号分量都包含了原始信号不同频段的特征信息。
小波包变换过程如图1所示。
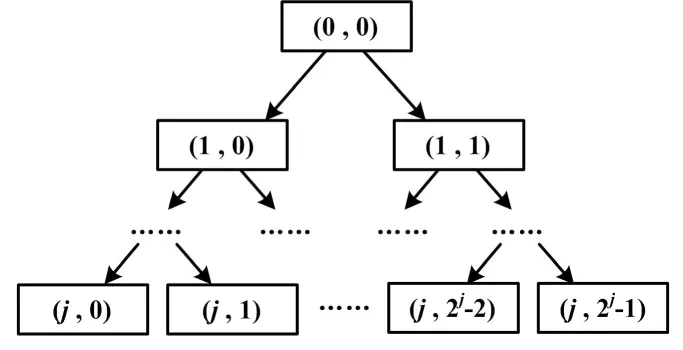
图1 小波包变换过程示意图
与小波变换相比,WPT能够提高信号通频段的分辨率,更为有效地挖掘信号中的潜在特征信息。其分解和重构算法如下[8]。
分解算法为:
(1)
重构算法为:
(2)

2 多尺度熵
MSE是在样本熵算法基础上发展而来的一种能够在不同尺度上衡量信号复杂度的方法。给定一个长度为L的序列{x1,x2,…,xL},其多尺度熵的具体计算过程如下[9]。
①对时间序列进行粗粒化处理。
(3)
②根据尺度因子τ的变化,得到长度为N=L/τ的序列,并构成m维矢量[Y(τ)(1),Y(τ)(2),…,Y(τ)(N-m+1)]。其中:Y(τ)(i)=[y(τ)(i),y(τ)(i+1),…,y(τ)(i+m-1)](1≤i≤N-m+1)。
③定义尺度τ上矢量Y(τ)(i)和Y(τ)(j)对应元素差值的最大绝对值为矢量间的距离。
d[Y(τ)(i),Y(τ)(j)]=max|y(τ)(i+k)-y(τ)(j+k)|
(4)
计算各i值下Y(τ)(i)与其他矢量Y(τ)(j)间的距离。
④给定一个相似容限r,统计各i值下d[Y(τ)(i),Y(τ)(j)]小于r的数目及其与距离总数的比值。

(5)
(6)
⑥对(m+1)维矢量重复步骤②~⑤,得到Cτ,m+1(r)。
⑦当长度L为有限值时,序列的样本熵值为:
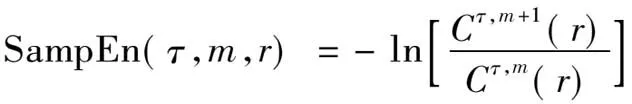
(7)
⑧多尺度熵的定义为:不同尺度因子τ下样本熵值的集合。则原始序列的多尺度熵为:
MSE={τ|SampEn(τ,m,r)}
(8)
3 概率神经网络
PNN是由径向基神经网络发展而来的一种前馈神经网络。其在径向基神经网络基础上,融合了概率密度函数估计和贝叶斯理论,以指数函数替代传统神经网络中常用的S型函数作为激活函数,具有训练简便、分类性能强等诸多优势。PNN一般由输入层、模式层、求和层和决策层构成,其结构如图2所示[10]。

图2 概率神经网络结构示意图
输入层将输入样本传递至模式层各节点,模式层与输入层通过权值ωij相连,进行加权求和,并通过非线性算子g(zi)运算后,传递给求和层。
(9)
该层各个模式单元的输出为:

(10)
式中:X为输入样本;Wi为输入层与模式层间权值矩阵;σ为平滑系数。
求和层将对应样本中同一类别的模式层传递输出进行累加,即:
(11)
式中:m为样本个数。
决策层接收求和层输出的各类别概率密度函数。概率密度函数最大的神经元输出为1,其对应的类别即为样本的识别结果;其他神经元输出则为0。
4 故障诊断流程
本文融合小波包变换、多尺度熵在信号特征提取上的优势以及概率神经网络强大的模式辨别能力,提出一种基于WPT-MSE和PNN的电机轴承故障诊断方法。故障诊断流程如图3所示。

图3 故障诊断流程图
故障诊断具体步骤如下。
①设置WPT的处理层数,对采集到的每个信号样本进行分解重构,得到相应的子带信号分量。对于WPT处理层数的选取,如果设置的层数过小,信号划分不够精细;反之,如处理设置的层数过大,则所得的子带信号分量带宽过窄,包含的特征信息过少,不利于特征信息的获取。综合考虑上述原因,本文设定WPT的处理层数为2层。
②计算每个信号样本分解所得子带信号分量的MSE,并构造相应的特征向量。MSE的计算结果主要受嵌入维数m和相似容限r这两个参数的影响。m越大,在动态重构序列的联合概率时,蕴含的细节信息越丰富;但m取值过大,会造成计算负担过重。综合考虑,本文设定m=2。r取值过大,会丢掉许多统计信息;反之,则容易受噪声的干扰,得到的统计特性效果不理想。因此,r一般取0.1SD~0.5SD(SD为原始数据的标准差),本文设定r=0.15SD。至于对MSE计算结果影响较小的样本长度L和尺度因子τ这两个参数的选取,本文分别取L=2 048、τ=10。
③通过WPT和MSE提取各样本的特征向量后,将训练样本的特征向量输入PNN,对神经网络进行训练。
④将测试样本的特征向量输入到训练好的PNN中,通过网络的输出结果来判别轴承的状态。
5 实例验证
利用西楚大学电气工程实验室的公开实测数据来验证所述方法的有效性。试验采集了SKF6205电机轴承在正常状态、内圈故障、外圈故障和滚动体故障等不同故障类型及不同损伤程度下的7种状态数据。试验过程中,电机转速为1 797 r/min,采样频率为12 kHz,对每种轴承状态均采集50个信号样本,样本长度为2 048点;从每种轴承状态的样本集中随机选取10个用于训练,另外40个作为测试样本进行测试。信号样本的具体描述如表1所示,轴承的7种工作状态分别用序号C1~C7表示。

表1 信号样本的具体描述
不同轴承状态样本的波形完全不同,轴承正常状态波形与内、外圈故障波形存在较大差异,但是与滚动体故障波形间的差异则不够明显。此外,对于同一故障类型,很难准确区分不同损伤程度的信号样本。为此,通过小波包和多尺度熵来提取信号样本的特征,并利用概率神经网络作为分类器来识别电机轴承的不同状态。
首先,对各个信号样本进行WPT处理。本文设定的处理层数为2层,因此每个样本经分解重构后得到4个频段由高至低排序的子带信号分量,并且与原信号相比,所得各子带信号分量复杂度有所降低。
利用WPT对各个样本进行处理后,计算样本分解重构所得子带分量的MSE,并构造相应的特征向量。由于本文选取的MSE尺度因子τ为10,因此每个信号样本经过WPT、MSE提取特征后,得到一个由4×10=40个元素组成的特征向量。轴承不种状态样本的特征向量如图4所示。
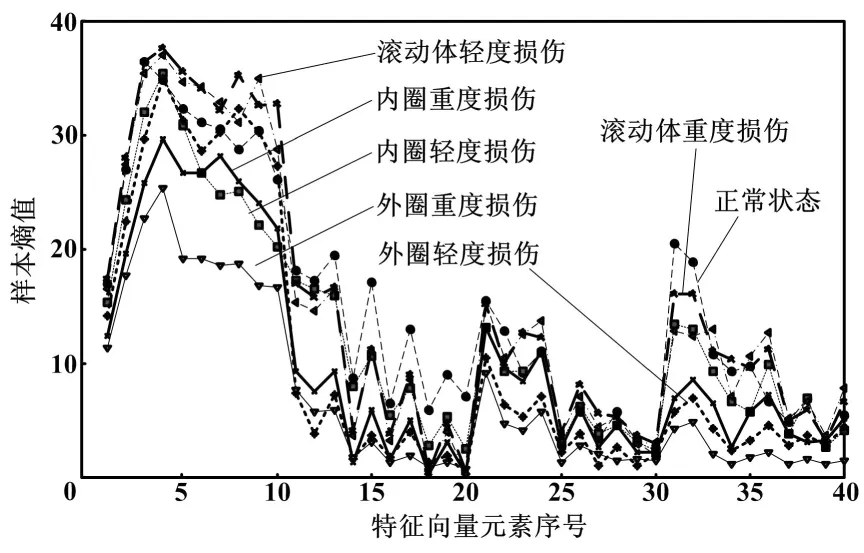
图4 轴承不种状态样本的特征向量示意图
通过观察图4可以发现,特征向量大部分序号位置对应的样本熵值可以很好地区分轴承不同状态,但是少数序号位置对应的样本熵值存在彼此接近的情况,由此表明熵值的可区分性不同。
对于电机轴承的7种状态,共有50×7=350个样本。在每种状态随机选取10个样本用于训练PNN网络,构成一个包含10×7=70个样本的训练集,剩余的40×7=280个样本则组成测试集。为了验证本文所述特征提取方法的可行性及优势,利用3种方法分别提取信号样本的特征。构造相应的特征向量后,将训练集的特征向量输入到PNN中进行网络训练,利用测试集的特征向量对训练好的网络进行检验。其中,方法一是本文提出的WPT结合MSE的方法,方法二直接计算样本的MSE作为特征参量,方法三采用文献[6]提出的EMD结合MSE的方法。3种特征提取方法识别准确率对比如表2所示。
由表2可知,方法一识别准确率最高,无论是单一状态判别还是整体识别,准确率均达到100%。方法二的整体识别准确率最低,为86.79%,且C7状态(滚动体重度损伤)的识别准确率极低,仅为25%,其中大部分C7状态样本被误判为C6状态(滚动体轻度损伤),说明直接以MSE为特征难以区分不同损伤程度的滚动体故障,而将WPT与MSE相结合则可以更好地刻画信号样本的本质特征,这也验证了WPT预处理的必要性。方法三的整体识别准确率为89.64%,除了C1状态(正常状态)外,其他状态类别均存在误判,且与方法一相比,识别准确率存在很大差距。究其原因,主要是由于EMD属于一种自适应信号处理手段,作为预处理方法在分解原始信号样本时表现得不够稳定,从而对后续分类效果造成不利影响。
上述对比结果表明,本文所述的WPT结合MSE方法能更好地实现对信号样本特征信息的提取,并且本文提出的基于WPT-MSE和PNN的诊断方法能够实现对电机轴承状态的准确判定。

表2 三种特征提取方法识别准确率对比
为了进一步验证PNN作为分类器的优越性,在训练样本集和测试样本集完全相同的情况下,利用WPT结合MSE提取样本特征并构造特征向量后,训练传统的BP神经网络并进行测试。PNN和BP网络识别结果对比如表3所示。

表3 PNN和BP网络识别结果对比
由表3可知,与PNN网络训练过程相比,BP网络的耗时更长,且样本整体识别准确率也低于PNN网络。由此表明,无论在网络训练速度还是分类准确率方面,PNN网络均优于传统BP网络。
6 结束语
本文提出了一种基于WPT-MSE和PNN的电机轴承故障诊断方法,通过WPT对信号样本进行分解重构处理,得到若干子带信号分量;利用MSE来描述各子带信号分量的状态特征,并构造相应的特征向量;通过PNN网络来识别电机轴承的不同工作状态。实际数据对比分析结果表明,与直接采用MSE方法以及EMD结合MSE的方法相比,WPT结合MSE的方法能更好地实现信号样本特征信息的提取。与传统BP神经网络相比,PNN网络在训练速度及分类精度上更具优势。本文提出的诊断方法能够有效区分电机轴承处于不同故障类型、不同损伤程度时的工作状态,得到可靠、准确的故障识别结果,从而为实际工程应用提供一定的参考。
[1] 马立新,黄阳龙,范洪成,等.基于自适应变异微粒群优化SVM的电机轴承故障诊断方法[J].电力科学与工程,2016,32(2):66-71.
[2] 罗忠辉,薛晓宁,王筱珍,等.小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J].中国电机工程学报,2005,25(14):125-129.
[3] 郑近德,程军圣,胡思宇.多尺度熵在转子故障诊断中的应用[J].振动、测试与诊断,2013,33(2):294-297.
[4] COSTA M,GOLDBERGER A L,PENG C K.Multiscale entropy analysis of biological signals [J].Physical Review E,2005,71:1-18.[5] 张龙,张磊,熊国良,等.基于多尺度熵的滚动轴承Elman神经网络故障诊断方法[J].机械科学与技术,2014,33(12):1854-1858.[6] 秦喜文,高中华,董小刚,等.利用经验模态分解和多尺度熵的滚动轴承故障诊断研究[J].制造业自动化,2015,37(11):67-70.[7] 杨凌霄,朱亚丽.基于概率神经网络的高压断路器故障诊断[J].电力系统保护与控制,2015,43(10):62-67.
[8] 向玲,鄢小安.基于小波包的EITD风力发电机组齿轮箱故障诊断[J].动力工程学报,2015,35(3):205-212.
[9] 李莉,朱永利,宋亚奇.多尺度熵在变压器振动信号特征提取中的应用[J].振动、测试与诊断,2015,35(4):757-762.
[10]陈慧,张磊,熊国良,等.滚动轴承的MSE和PNN故障诊断方法[J].噪声与振动控制,2014,34(6):169-173.
Fault Diagnosis Method Based on WPT-MSE and PNN for Motor Bearing
XU Jianjun1,DU Qiangnan1,XU Jianyong2,XUE Guohua2
(1.School of Electrical Information Engineering,Northeast Petroleum University,Daqing 163318,China;2.Zhongru Construction Group Co.,Ltd.,Rugao 226500,China)
Rolling bearing is an important element in the motors;under actual operating condition,the interference of background noise is serious,so effective feature extraction and accurate fault judgment for motor bearings are difficult to be achieved.In order to solve this problem,a diagnosis method based on wavelet packet transform(WPT),multiscale entropy(MSE) and probabilistic neural network (PNN)is proposed.Firstly,the acquired signal samples are processed using wavelet packet transform,the original signals are decomposed into the corresponding subband signal components,and the cross interferences between the complex components in the original signals could be reduced.Then,the multiscale entropy of each subband signal component obtained is calculated,and the extracted multiscale entropy is used to construct the feature vectors which can characterize the operating conditions of the motor bearings.Finally,the feature vectors are input into the probabilistic neural network,and the different fault types and injury degrees of the motor bearings can be identified automatically.The analysis results of the measured data show that the diagnosis method proposed can effectively identify the different operating conditions of the motor bearings,which provides a new reference for fault diagnosis of motor bearings and has a certain value for engineering applications.
Probabilistic neural network; Wavelet packet transform; Multiscale entropy; Motor bearing; Fault diagnosis
徐建军(1971—),男,博士,教授,主要从事电力理论与新技术的研究。E-mail:123939274@qq.com。 杜蔷楠(通信作者),女,在读硕士研究生,主要从事电力理论、故障诊断方向的研究。E-mail:759670887@qq.com。
TH17;TP27
A
10.16086/j.cnki.issn1000-0380.201704020
修改稿收到日期:2016-11-29
