神经网络预测在无刷直流电机调速中的应用
2017-04-24付光杰林雨晴牟海维
付光杰,林雨晴,牟海维
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.东北石油大学电子科学学院,黑龙江 大庆 163318)
神经网络预测在无刷直流电机调速中的应用
付光杰1,林雨晴1,牟海维2
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.东北石油大学电子科学学院,黑龙江 大庆 163318)
针对传统无刷直流电机调速系统中转速控制器参数不易设定、传统控制中依据反馈信号控制当前状态会产生延迟且转速预测精度较低等弊端,提出了一种改进的神经网络预测控制方法。该方法将BP神经网络和预测控制相结合,并在转速预测环节利用曲率圆作为参考模型实现神经网络的训练。通过设置适当的输入层和隐含层,实现了神经网络对误差信号的有效调节,并预测出电机下一时刻的转速,从而有效地减小了控制作用的延迟时间,使非线性控制系统的参数设定具有良好的准确性,并能提高无刷直流电动机的转速预测精度和准确度。仿真结果表明,神经网络预测控制能够在1 000~3 000 r/min的调速范围内,有效改善系统的控制精度、实时性和稳定性。该方法也可应用于轧机、变频空调压缩机等调速控制系统。
直流电机; 电机调速; 转速预测; 神经网络; PID控制; Matlab
0 引言
无刷直流电机根据转子位置控制电力电子器件进行换向,克服了普通直流电机由电刷滑环构成机械换向器的各种弊端,因此被广泛应用于汽车、变频空调等工业工控领域[1]。在控制方法上,由于无刷直流电机属于非线性、强耦合系统[2],采用经典PID控制的控制效果往往不够理想,目前使用较普遍的是智能控制或智能控制与PID相结合的控制方法。为进一步改善调速效果,本文根据无刷直流电机控制方法的研究现状,提出了一种神经网络预测控制方法。该方法利用神经网络对电机的转速进行预测,并根据预测的电机转速指导并调整当前的转速,以提高调速系统响应的快速性、准确性和稳定性。
1 无刷直流电机的数学模型
无刷直流电机主要由电机本体、位置检测装置、驱动控制器和电力电子电路构成,其结构框图如图1所示。

图1 无刷直流电机结构框图
无刷直流电机在工作时,由转子位置检测装置检测出转子位置;根据转子所在的位置,由驱动控制器控制相应电力电子器件的导通和关断,以达到换向的目的[3]。无刷直流电机电压方程如式(1)所示。

(1)
式中:μA、μB、μC为无刷直流电机的定子绕组各相电压;iA、iB、iC为绕组各相电流;eA、eB、eC为绕组各相反电动势;RS为绕组电阻;L为三相绕组自感;M为互感。
无刷直流电机的线电压反电动势与转速n的关系为:
E=CeΦδn
(2)
式中:Ce为反电动势系数;Φδ为每极气隙磁通。
不考虑开关器件动作过渡过程,并忽略电枢绕组的电感,则无刷直流电机电枢每相电流为:
(3)
式中:Ud为电源电压;IA为每相电枢电流;RA为电枢绕组平均电阻;ΔU为功率晶体管饱和管压降。
2 神经网络预测控制
2.1 神经网络预测控制方法
目前,用于无刷直流电机的控制方法大多根据电机当前时刻的转速值与给定转速值之间的误差情况进行控制[3]。在实际应用中,电机的转速变化往往较大,尤其是在电机启动过程中或受到外界扰动情况下[4],利用电机当前时刻的转速进行控制往往存在滞后性[5]。
神经网络预测控制利用神经网络预测出电机的转速,并根据该预测值对当前电机转速进行控制。首先对无刷直流电机的转速信号进行反馈,通过神经网络预测出下一时刻电机的转速值,并将其与给定转速进行比较,求出转速误差;然后通过神经网络产生控制信号,进而通过调压等手段对电机的转速进行调节。其中,神经网络预测采用参考模型法,也就是将转速信号与预先设置的曲率圆参考模型的特征进行对比,实现转速预测。得到转速误差后,为了弥补PID对非线性系统控制不理想的缺陷[6],本设计采用神经网络生成非线性控制信号,其控制作用f与误差E的关系曲线如图2所示,相当于控制信号的参考模型。

图2 控制作用f与误差E的关系曲线
2.2 神经网络参考模型转速预测
本文采用基于参考模型的神经网络转速预测方法。首先根据电机转速变化的特点建立一个参考模型,电机转速变化具有实时性、连续性和非线性的特点。典型的转速变化规律是当电机启动后,转速值迅速升高,达到给定转速后产生超调量,随后逐渐在给定转速附近上下震荡多次后与给定转速保持一致。电机转速与时间的关系曲线如图3所示。

图3 电机转速随时间变化典型曲线
图3中:n*为给定转速值;k为曲线上任一点切线的斜率值,即转速的瞬时变化率。
(4)
k的取值范围为(-∞,+∞),每当转速变化经历一次波峰和波谷的波动时,其转速变化率便由正无穷大逐渐减小到零,这时转速达到波峰;然后转速变化率继续减小到负无穷大再增大到零,这时转速达到波谷;最后转速变化率由零再次增大。转速的变化率与转速的变化是紧密相连的。为了更好地预测出转速值,本文采用曲率圆参考模型。对于标准圆,有:
(x-a)2+(y-b)2=r2
(5)
取其上半部分作为神经网络预测的曲率圆参考模型,如图4所示。电机启动后,利用神经网络,并根据曲率圆参考模型中的坐标值和曲率,对下一时刻的电机转速进行预测。

图4 曲率圆参考模型
图4中:A,B,…,G为曲率圆上的点;kA,kB,…,kG为这些点的切线斜率,它们代表着曲率圆上的变化趋势。圆上点(x0,y0)处的切线方程可表示为:
(x0-a)(x-a)+(y0-b)(y-b)=r2
(6)
当电机转速进行反复波动调整时,其变化率在曲率圆模型上体现为沿着A,B,…,G,A方向的切线的斜率变化。本文采用前馈型BP神经网络,包括输入层、输出层以及多个隐含层。设网络的感知器是由单层的s个感知神经元构成,并通过一组权值{wij}(i=1,2,…,s,j=1,2,…,r)与r个输入相连,获得输出信号;根据网络结构,可知第i个输出神经元(i=1,2,…,s)的加权输入和ηi及其输出ai为:
(7)
ai=f(ni+bi)
(8)
输出层的输出为:
ok=f(netk)k=1,2,…,r
(9)
利用神经网络,根据预定的参考模型对转速进行预测,能够使得预测转速曲线更加平滑,且更接近真实转速值。
2.3 神经网络预测控制影响因素
在神经网络预测控制中,电机转速预测的准确程度对整体系统的影响比较大[7]。根据曲率圆模型对神经网络进行训练,神经网络应具有足够的隐含层数量,以保证相应神经元权值的进一步优化[8],使得转速预测曲线更加平滑,且更接近真实值。对于BP神经网络而言,权值系数的修正公式为:
(10)
式中:η和α分别为训练效率和惯性系数;E(k)为性能指标函数。
(11)
权值修正时,反传误差信号δ为:
(12)
令t+1为训练的第t+1步,α为平滑因子,且0<α<1,则:wij(t+1)=wij(t)+ηδiOi+α[wij(t)-wij(t-1)]
(13)
随着隐含层神经元数量的增加,权值能够得到更精确的修正,从而更能平滑地接近真实值;但其会增加网络的复杂程度[9],输入层的变量个数对最终的预测转速也会产生一定的影响。在实际应用中,应当充分考虑系统的复杂程度和所需要的精确程度,设置合理的隐含层和输入变量数[10]。此外,对于曲率圆参考模型,如果沿纵轴方向拉伸、沿横轴方向压缩,有:
(14)
曲率变化率为:
(15)
根据式(14)、式(15),可以使竖直方向上的曲率半径增大,并使得转速预测的变化率增大。当转速快速变化时,更能够对转速快速跟踪,但会削弱转速基本不变时的稳定性。反之,如果式(14)中的r2>r1>0,那么曲率圆参考模型的水平方向曲率半径增大,有利于在转速基本稳定时提高转速预测的准确性,但不利于转速快速变化时的预测。因此,参考模型应根据系统的预期性能指标选取。
2.4 无刷直流电机调速系统
根据神经网络预测的原理以及无刷直流电机的调速特点,改进的调速系统框图如图5所示。

图5 改进的调速系统框图
系统中包括转速预测与转速控制两个神经网络,分别用曲率圆模型和误差控制规律曲线模型对网络进行训练,使其具备预测与控制的能力。利用电机转速作为反馈信号,经过转速预测求出下一时刻转速,与给定转速比较后通过控制网络对电源电压进行控制,最终使电机实际转速达到给定值。
3 仿真与研究
3.1 网络训练与参数设置
利用Matlab对改进的调速系统进行仿真,根据神经网络模型预测的原理,参考模型为曲率圆模型;利用Simulink工具箱中的信号发生器产生曲率圆数据,从中选取50个采样点,以每一个采样点以及相对上一个采样点的变化率为输入,以下一个采样点为输出,对预测神经网络进行训练。其中:样本分配为训练70%、验证15%、测试15%,隐含层设为13。
根据网络训练的状态检测,该网络在第77次迭代后可以得到最优权值,网络处于最优状态;同理,根据双曲正切规律对控制网络进行训练,作为调速系统的控制器部分。无刷直流电机模型的额定电压为500 V,额定负载为10 N·m,额定转速为3 000 r/min,仿真时间设为0.2 s,算法为变步长ode23,调速系统采用空载启动,并在0.1 s时加入额定负载,同时产生扰动。
3.2 仿真分析
给定转速的神经网络转速预测波形如图6所示。
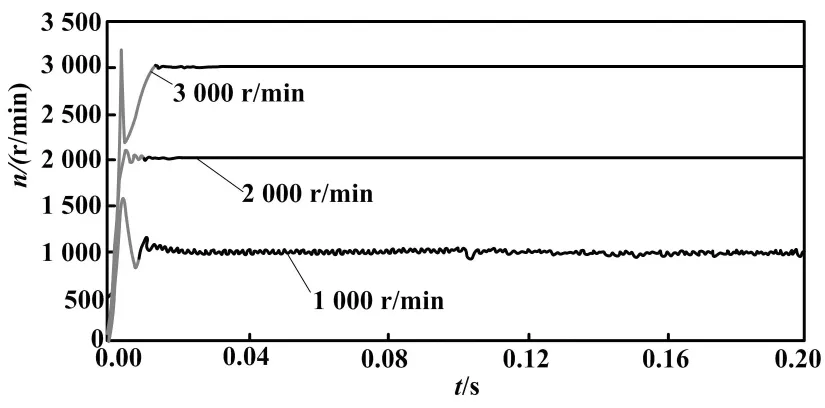
图6 给定转速的神经网络转速预测波形
从图6可以看出,根据神经网络参考模型预测法得到的转速预测波形与实际转速基本吻合,主要在转速上升阶段的末期有些偏差,但这有助于减小实际转
速的超调量,尽快使转速稳定在给定值附近。
当给定转速降低时,超调量和静差率将逐渐增大,按照2%的误差允许范围,在给定1 000 r/min时接近误差允许范围,因此在1 000~3 000 r/min的调速范围内,神经网络预测控制都是适用的。
4 结束语
本文主要研究了无刷直流电机的控制方法,对于无刷直流电机的调速系统,为达到理想的控制效果,采用PID控制时需要对参数进行反复的调节。智能控制与PID结合使用将改善控制效果,但根据当前转速进行控制会产生一定的延迟。为此,在神经网络控制的基础上提出了神经网络预测控制:利用曲率圆作为参考模型,设置适当的输入层和隐含层,对神经网络进行训练;得到转速预测网络,并预测出电机下一时刻的转速;与给定转速比较后,再由控制网络得到控制信号,通过调压调速实现转速的控制。由仿真波形可以看出,神经网络预测控制下调速系统的快速性和稳定性更加理想,并适用于较大的调速范围,预测波形比较接近真实值。本文的研究成果不仅能够改善无刷直流电机调速系统的控制效果,而且可推广至其他控制领域。
[1] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3):25-34.
[2] 刘国海,金鹏,魏海峰.无刷直流电机调速系统神经网络逆控制[J].电工技术学报,2010,25(8):24-30.
[3] 胡云宝,王加祥,曹闹昌,等.基于RBF神经网络无刷直流电机调速系统[J].微电机,2013,46(1):63-66.
[4] 付光杰,赵子明.改进转速预测控制的无刷直流电机调速研究[J].组合机床与自动化加工术,2014(8):67-71.
[5] 郭伟,张爱华,陈琛,等.无刷直流电机调速优化控制与仿真[J].计算机仿真,2015,32(10):360-364.
[6] 伍铁斌,龙文,朱红求.复杂工业过程操作参数优化研究进展[J].自动化仪表,2016,37(3):1-4+8.
[7] 刘加存,梅其祥,李春辉.基于频分神经网络和预测控制的PID参数整定研究[J].系统仿真学报,2014,26(5):1176-1179.
[8] 樊兆峰,马小平,邵晓根.神经网络预测控制局部优化初值确定方法[J].控制理论与应用,2014,31(6):741-747.
[9] 王霞,朱景伟.基于模糊PI控制的无刷直流电机调速系统[J].电气传动,2014,44(1):63-67.
[10]岳学磊,白鹏.关于无刷直流电机调速系统优化控制研究[J].计算机仿真,2015,32(10):414-419.
Application of Neural Network Prediction in Speed Regulation of Brushless DC Motor
FU Guangjie1,LIN Yuqing1,MU Haiwei2
(1.School of Electrical Engineering and Information,Northeast Petroleum University,Daqing 163318,China;2.School of Electronic Science,Northeast Petroleum University,Daqing 163318,China)
The parameters of the traditional speed regulation controller of brushless DC motor are difficult to be set up,and in traditional control,the prediction precision of the speed is low because of the delay caused by the current state is controlled in accordance the feedback signal.To overcome these disadvantages,the improved neural network prediction control method is proposed.With this method,the BP neural network is combined with the prediction control,and in the speed prediction section,the training of the neural network is implemented by using curvature circle as the reference model. Through setting appropriate input layer and hidden layer,effective regulation of the error signal for neural network can be achieved,and the speed of motor at the next moment can be predicted,thus the time delay of the control action is reduced effectively,to obtain excellent accuracy of the parameters set for nonlinear control system,and to enhance the prediction accuracy for speed of DC motor. The simulation results fully verify that the neural network prediction control can effectively improve the control accuracy of system within the range of 1 000~3 000 r/min,and real time performance and stability.The method can also be applied in other speed control systems,such as rolling mills,and compressors of VF air conditioning,etc.
DC motor; Motor speed regulation; Speed estimation; Neural network; PID control; Matlab
国家自然科学基金面上项目(51374072)、东北石油大学培育基金资助项目(py120219)、东北石油大学研究生创新科研基金资助项目(YJSCX2014-028NEPU、YJSCX2015-028NEPU)
付光杰(1962—),女,博士,教授,博士生导师,主要从事电力电子技术与智能控制方向的研究。E-mail:fgjmhw@163.com。
TH7;TP29
A
10.16086/j.cnki.issn1000-0380.201704003
修改稿收到日期:2017-01-11
