初中数学几何教学中运用模型教学的研究

徐辉

数学是学生学习的基础学科.几何知识作为数学学科中重要模块，不仅能培养学生的空间想象能力，还能帮助学生构建完善的数学思维，提高学生运用数学知识的能力.在新课程背景下，教师应创新几何教学方式，合理运用模型教学，引导学生用模型的方式解决几何问题，进而提高学生的实践能力.

一、利用模型在几何中的教学内涵，解决几何问题

几何模型教学主要是指借助平面图形或者立体图形，帮助学生形成几何思维的一种新型模式.在教学过程中，教师可以将几何知识点的教学内涵作为基础，结合对应的模型，引导学生理解几何知识，进而解决几何问题.

例如，在讲“相似三角形”时，为帮助学生理解相似三角形的内涵，更好地运用在勾股定理中，教师可以借助“相似几何模型”.首先，在黑板或者PPT上展现出相似三角形的模型（图略）.其次，让学生寻找有关“相似三角形”的性质.在这个过程中，学生可以通过加线、量角度等方式，教师要给予学生充分的时间探讨.最后，得出相似三角形的定义与性质：（1）相似三角形的周长比等于相似比.（2）相似三角形对应高、对应边等线段的比均等于相似比.（3）相似三角形面积的比等于相似比的平方.教师可以结合图形讲解几何知识的内涵，促使学生根据几何模型去解题.

二、利用模型对比差异建立的联系，加深理解几何问题

通过模型之间的差异，建立几何之间的联系，不仅能加深学生对于几何问题的理解，还能帮助学生掌握几何知识的原理，提高学生运用几何知识的能力.

例如，在讲“全等三角形”时，教师可以灵活运用“手拉手几何模型”和“等积变换几何模型”，引导学生得出证明三角形全等的定理.

首先，在黑板上或者PPT上展示出“手拉手几何模型”和“等积变换几何模型”，

如图1和图2.其次，引导学生找出图2中△ABE≌△DBC和图3中△ACD≌△BCD，从两个模型的差异中寻找共同点，进而让学生掌握有关全等三角形的性质与定理，使学生遇到此类模型时能及时联系到相关几何知识，从而帮助学生增强学习数学的信心.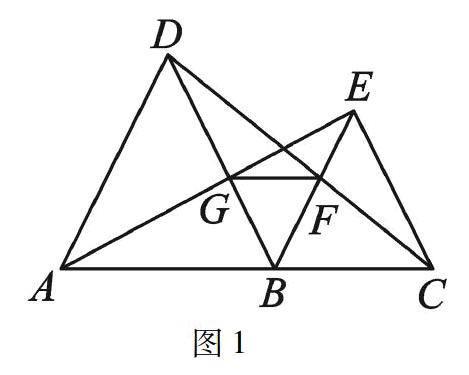

三、利用模型结合理论知识与实际，提高学生的实践能力

几何知识对学生的逻辑思维能力、空间想象能力要求较高.在讲解抽象的几何知识时，教师可以将知识具象化，从生活中的几何模型入手，加强理论知识与实践活动之间的联系，提高学生的解题能力.

例如，在讲“对称图形-圆”时，教师可以通过生活化的教学方式，引导学生寻找生活中熟悉的圆形，如“车轮”、“饭碗”、“圆形镜”等，再向学生展示有关圆形的设计或者建筑，消除学生对于圆形知识的陌生感，以图片、声音等形式吸引学生的注意力，帮助学生形成初步的圆形几何模式.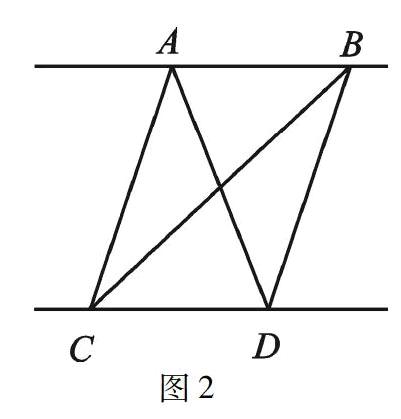

四、利用模型培养学生的数学思维，提高学生的综合能力

几何模型应来源于学生熟悉的现实生活，并能有效培养学生的数学思维.因此，教师可以适当布置针对性的课后练习，提高学生的综合能力.

例如，在讲“勾股定理”后，教师可以布置如下习题：（1）如果Rt△ABC两直角边边长分别为k2-1，2k（k大于1），那么它的斜边长为多少？（2）已知边长为17cm，一条直角边长为8cm，该直角三角形的面积为多少？（3）有一个Rt△ABC，两直边AC=6cm、BC=8cm，现将直角边AC沿着∠CAB的角平分线AD折叠，使其落在斜边AB上，与AE重合，求CD的长.通过以上不同难度的几何题目，促使学生记忆勾股定理：a2+b2=c2.

综上所述，将模型教学应用在初中数学几何教学过程中具有重要意义，不仅能帮助学生理解数学知識内涵，合理解决有关几何问题，还能培养学生理论联系实际的能力，提高学生的综合素养.在教学过程中，教师应综合考虑学生的个性特征、几何教学内容、学生的数学基础等，科学运用模型教学，降低学生理解几何知识的难度，引导学生构建完善的数学知识系统，从而促使学生全面发展.