基于MCS和PERT的引水工程工期风险分析
2017-04-20李东亮
李东亮
(辽宁省东水西调工程建设局,辽宁 沈阳 110000)
基于MCS和PERT的引水工程工期风险分析
李东亮
(辽宁省东水西调工程建设局,辽宁 沈阳 110000)
由于自身特点、环境条件的影响,引水工程建设的风险因素较多。综合运用蒙特卡洛方法(MCS)和经典计划评审技术(PERT),对引水工程的工期风险进行分析,论述了其模型建立方法,并结合工程案例,探讨了网络计划图绘制、网络计划活动时间的三时估计、MCS的模拟等环节。
引水工程;工期风险;MCS;PERT;建立模型;三时估计
0 引言
大型引水工程由于投资大、建设周期长、建设过程的连续性和协作性、受自然条件和社会环境制约性强、牵涉利益主体多等,所以影响其施工建设的风险因素众多,且关系错综复杂。工期风险是大型引水工程项目风险中的核心风险之一。因为工期的延误将使各参与方的效用下降,使整个项目的收益降低。
蒙特卡洛仿真方法(Monte Carlo Simulation,简称MCS)是一种利用计算机进行随机抽样或模拟实验的方法。其原理是,通过产生随机数来抽取符合各活动持续时间概率分布的样本值,并以抽取的样本值为基础,进行网络计划的工期模拟计算,记录该样本集合的总工期、关键路径和关键活动[1]。计划评审技术(Program Evaluation and Review Technique,简称PERT)是针对不确定性较高的工作项目,以网络图规划整个专案,以排定期望的专案时程的方法[2]。笔者试综合运用MCS与PERT两种方法,对大型引水工程的工期风险进行分析,以期找出计划工期的可能完成规律,并预测完成的可能性。
1 模型的建立
1.1 PERT网络计划技术
经典PERT方法认为,各工作活动持续时间的不确定性可以用一定的概率分布来表达,可以看作服从某种概率分布的随机变量。PERT方法有如下假设:(1)任意工作的持续时间可以用期望值、方差的概率分布特征来描述其不确定性。(2)任意两工作的持续时间相互独立,互不相关。(3)时间参数计算可采用关键路径(Critical Path Method,简称CPM)网络时间参数计算,即将各个活动持续时间的期望值当作活动的确定持续时间,将PERT网络转化为CPM网络进行计算。(4)工期最长的路径为关键路径,且关键路径时间长度与非关键路径时间长度相比足够长。(5)关键路径上的工作数目足够多。
统计规律和大量的研究成果表明,当工程项目的网络足够大时,工期的分布不受工作持续时间分布的影响,近似地服从正态分布[3]。
1.2 分布函数介绍[4]
β分布在估计区间(a,b)内的概率密度表达式如式(1)所示。
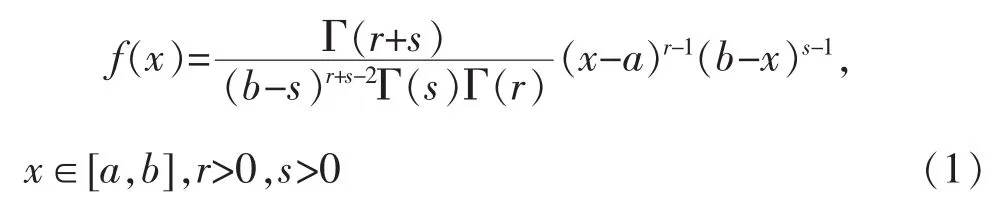
其中,r和s决定分布的形状,一般有左偏、右偏和对称3种。
特征值期望和方差如式(2)和式(3)所示。
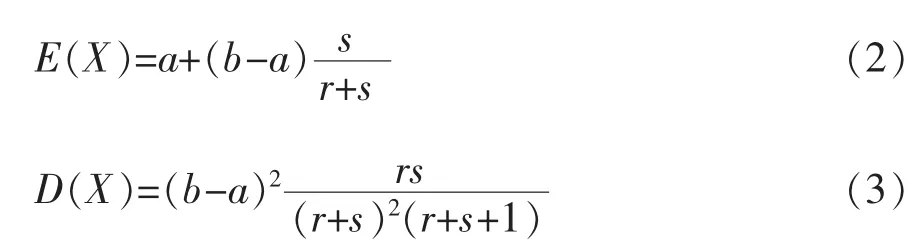
1.3 MCS方法求解PERT
MCS工期风险分析的步骤为[5]:(1)对引水工程进行施工方案分析,编制网络计划。(2)对网络计划的活动时间进行三时估计。(3)假设各个活动时间参数服从β,采用舍选取样法抽取进行抽样。(4)确定MCS计算参数、分组数及输出结果形式。(5)对每次模拟进行活动持续时间抽样、网络时间参数计算。(6)多次模拟,统计总工期及关键度指标(关键度等于活动在模拟中成为关键路径的次数n与仿真次数N之比)。(7)输出结果。
其中,第(3)步的抽样过程具体步骤为:(1)用“三点”法估计a、b、m值,计算r、s值。(2)计算f(x)的最大值f(m)。(3)形成两个[0,1]均值分布,产生随机数r1、r2。(4)计算f(a+(b-a)r1)的值。(5)判断f(a+(b-a)r1)/f(m)大于等于r2是否成立,若成立,则a+(b-a)r1即为服从β分布的随机活动时间。否则重复步骤(3)(4)(5),直至判断式成立为止。其抽样过程通过VB编程随机抽取得到。
在对活动进行三时估计后,从β(a,b,r,s)分布的参数已知,仅有r,s未知。依据PERT活动持续时间的均值、方差,按公式(4)计算r,s。
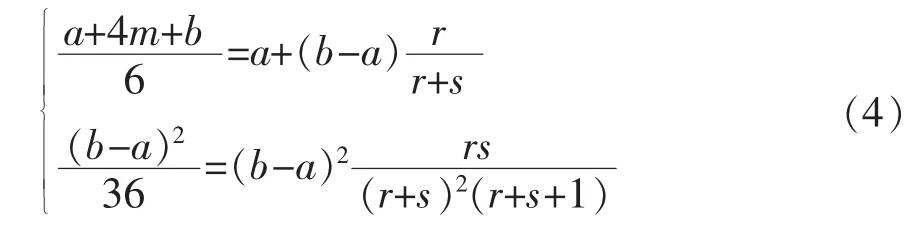
2 案例分析
2.1 工程简介
某引水工程起点位于北京市丰台区老庄子乡,沿五环路向南转向东,终点到亦庄水厂调节池,全长约27.2 km。根据工程规模和施工方法,将该工程分为上、下两段(分界点在京沪高铁的东侧),上段为2孔内径为3 400 mm的钢筋混凝土隧洞,初次衬采用浅埋暗挖法施工(局部明挖);下段为1孔内径为4 700mm的钢筋混凝土隧洞,初衬采用盾构法施工。
该工程第六标段的工作内容为输水洞线桩号7+262.04~8+440.04,中心导线全长1178 m,包括浅埋暗挖隧洞、11#、12#排气阀井、穿京良路、穿京山铁路等部分。
2.2 绘制网络计划图
由于整个标段的工作多且关系复杂,本文仅对其中的部分工程进行MCS模拟[6]。其网络计划如图1所示。
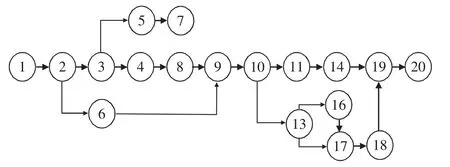
图1 双代号网络图Fig.1 Twin code network
2.3 对网络计划的活动时间进行三时估计
对网络计划的活动采用三时估计法进行估算,部分活动三时估计值如表1所示。
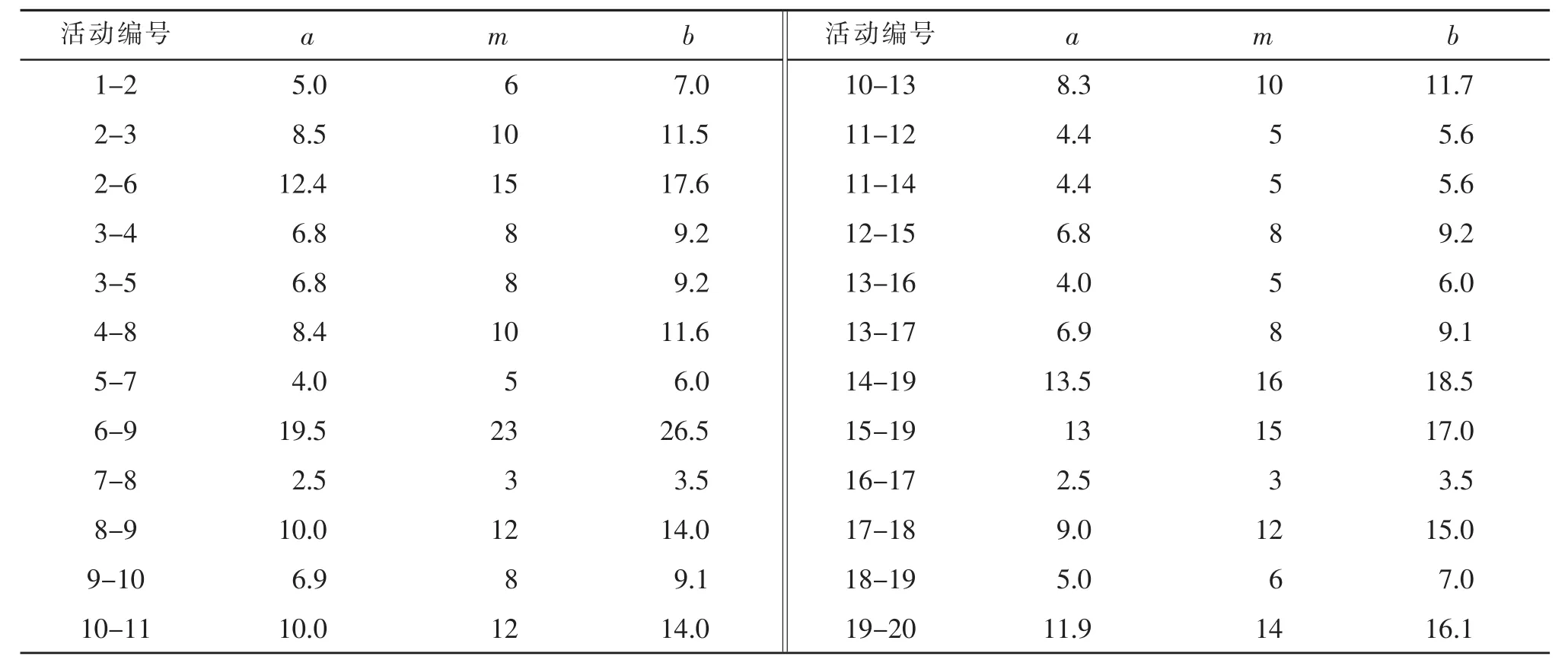
表1 活动三时估计值Tab.1 Time estimation of activitiy three
2.4 MCS模拟计算
按照工期风险分析步骤计算:共模拟10 000次,分为10组,完工工期分布如图2所示,完工工期累计概率分布如图3所示,期望工期为108.497 d,标准差为2.832 d。从活动的关键度来分析,运用蒙特卡洛模拟法避免了传统的经典PERT规定的关键线路的缺点,路线1-2-3-4-8-9-10-11-12-15-19-20的关键度为0.612,路线1-2-6-9-10-11-12-15-19-20的关键度为0.257,其他的路线关键度较小。因此,在施工过程中,要重点把握这2条路线上的活动,以确保工程的顺利进行。根据不同的计划工期,得出不同的完工概率,如表3所示。
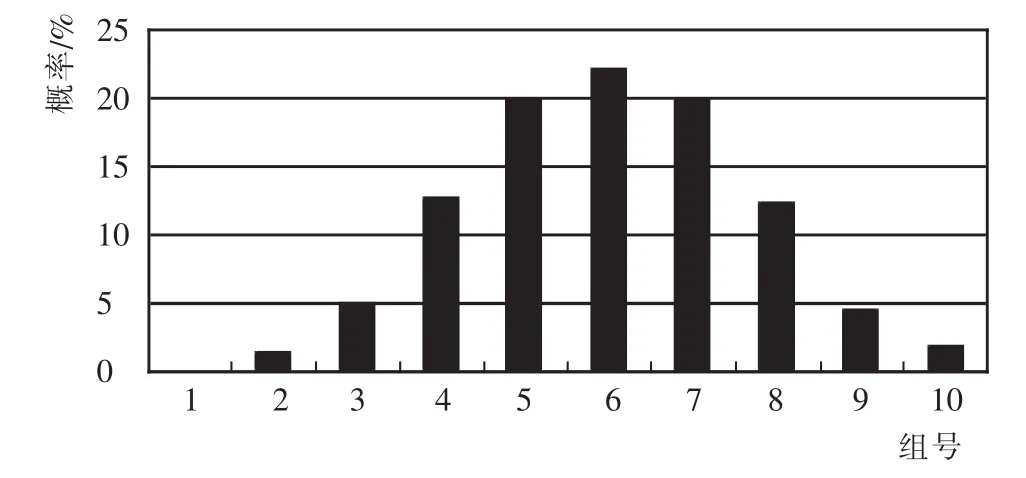
图2 完工工期概率分布Fig.2 Probability distribution of total project construction period
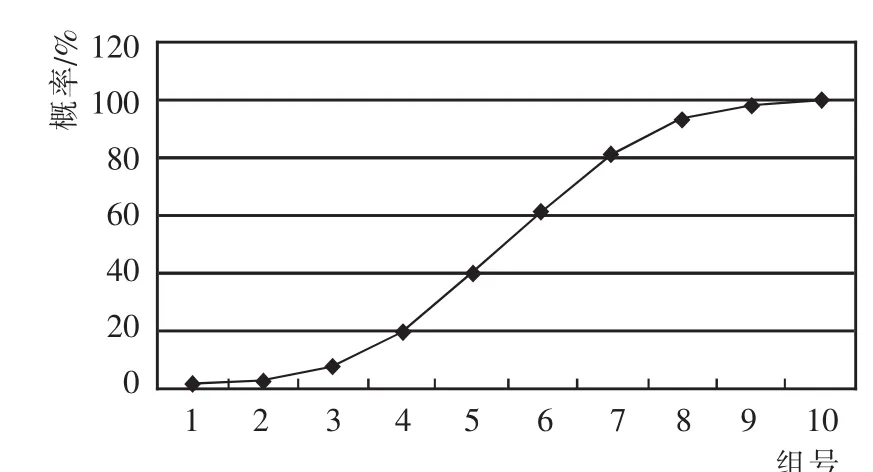
图3 完工工期累计概率分布Fig.3 Cumulative probability distribution of total project construction period

表2 活动关键度Tab.2 Key degrees of activity
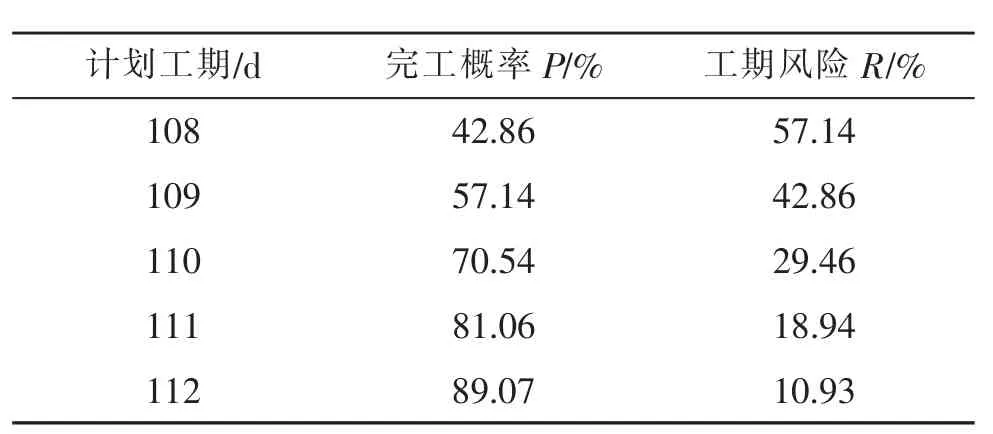
表3 计算结果Tab.3 Calculation results
由表3可知:完工工期要求越短,完工概率越小,工期风险越大;完工工期要求越长,完工概率越大,工期风险越小。
3 结语
蒙特卡洛法与计划评审技术相结合是工期风险分析的一种有效方法,但计算机模拟过程较为复杂。随着计算机技术的发展,借助计算机的处理能力,可以使整个计算过程变得简单快捷。该方法可以为承包人进行工期风险分析提供一条有效的途径。
[1] 陈群,孙磊.蒙特卡罗法在投标报价中的应用[J].武汉理工大学学报信息与管理工程,2009,6(3):503-506.
[2] 蔡晨,万伟.基于PERT/CPM的关键链管理[J].中国管理科学,2003,11(6):35-39.
[3] 李忠富.PERT网络工期分布规律初步探讨[J].哈尔滨建筑工程学院学报,1992(3):88-895.
[4] 陈家鑫.应用概率论[M].北京:科学出版社,1992:42-90.
[5] 李平,顾新一.PERT网络工期风险计算方法的研究[J].统计与决策,2004(5):16-17.
[6] 李东亮.大型引水工程施工工期风险研究[D].郑州:华北水利水电学院,2011.
[责任编辑 杨明庆]
TV51
B
10.13681/j.cnki.cn41-1282/tv.2017.02.005
2017-02-07
李东亮(1984-),男,河南周口人,工程师,硕士,主要从事水利工程管理等方面的工作。
