思维从曲折走向自然*
——以一道高考压轴题探究为例
2017-04-20福建省闽清县教师进修学校350800
福建省闽清县教师进修学校 (350800)
黄如炎
思维从曲折走向自然*
——以一道高考压轴题探究为例
福建省闽清县教师进修学校 (350800)
黄如炎
数学是自然的,数学是清楚的[1],因此数学教学应是清晰明理的.由于现行数学文本(包括教材、教辅、报刊等)的学术形态隐去了数学概念、结论、应用的形成与发展过程,以及应试教学重结果轻过程的行为,常使学生感到数学教学中有些 “规定”没有规矩,有些推理不讲道理,有些结论强加于人,这些问题严重阻滞了学生思维的发展.数学教学要遵循学生思维的自然形成,教师要对数学文本进行精心创作和深度开发,要根据学生已有的认知结构和学习经验,通过教学情境创设和导思探究活动,在一波三折,峰回路转,起伏跌宕的数学思维历程中,挖掘文本中看不见的数学发现、数学创造的思维过程,揭示蕴含在知识背后的核心素养、数学本质和思想方法,让思维从学生的头脑里自然地流淌出来.
高考压轴题蕴含着的丰富的数学核心素养的教育价值,承载着“四能”(发现和提出问题的能力,分析和解决问题的能力)的考察功能,对学生解题思维的形成极具挑战性,是培养发展学生思维的最好素材.本文以2016年全国高考(Ⅰ)卷理科数学压轴题的探究为例,谈如何让学生的思维从曲折走向自然.
1 标解疑惑
题目 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(Ⅰ)求a的取值范围;(Ⅱ)略.
命题组标准解答:f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
(ⅰ)设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.
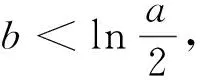
(ⅲ)设a<0,…,f(x)不存在两个零点.
综上,a的取值范围为(0,+∞)[2].
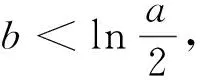
2 问题探究
基于学生存在的疑惑,笔者以“当a>0时,判定函数f(x)=(x-2)ex+a(x-1)2零点的个数”为问题,开展导思探究活动,教学过程如下.
师:请同学们回顾一下研究函数零点问题的经验.
众生:应用函数零点存在定理,注意数形结合,常用导数研究函数的图像和性质.
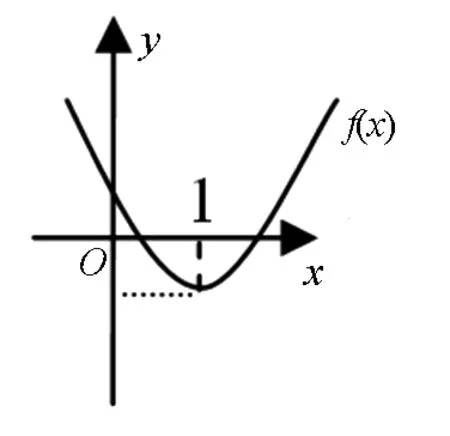
图1
生1(约2分钟思考与画图):f′(x)=(x-1)(ex+2a),当a>0时,f(x)在(1,+∞)上单调递增,在(-∞,1)上单调递减,f(1) =-e<0.如图1,f(x)在(-∞,1)和(1,+∞)上各有一个零点,故a>0时,f(x)有两个零点.
师:大家同意她的解法吗?
生2:怎知道f(x)图像左右两侧都是向上无限延伸?
生3:似乎理由也不够充分,根据零点存在定理,要在区间(-∞,1)和(1,+∞)上各找到一个数使其函数值大于零.
师:当x→±∞时,f(x)→+∞,说明生1所画图像正确.直觉有助于思维,但不能替代证明.
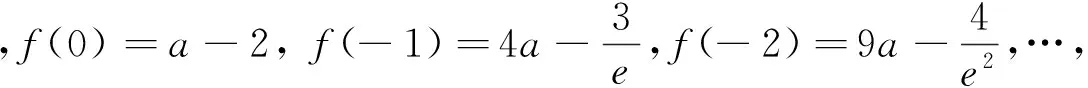
师:为什么寻找不到小于1的常数使其函数值大于零?能否从式子的形式结构进行研判?
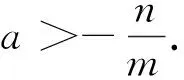
师:分析的好!x不能取常数那该取什么呢?
生5:根据以往经验取x关于a的式子,如取x= 1-a<1,f(1-a)=-(a+1)e1-a+a3,此式也不能保证大于零,因为还含e1-a难以计算.
众生(尝试失败,感到山穷水尽疑无路):取很多x关于a的式子都不能使其函数值大于零.
师:刚才我们的思维本质是寻找具体的x,当x<1且x为常数或x=g(a)时,f(x)>0.现在知道不可能了,那能否扩大寻找范围,如把寻找x=g(a)改为x 生6:为什么考虑寻找x 师:“数缺形时少直观,形少数时难入微”(数学家华罗庚语) 生7:“数形结合百般好,隔离分家万事休”(华罗庚语).由f(x)图像知当g(a) 众生:一阵掌声. 生8:x<1时,怎样寻找x 师:当x<1时,看可否把不等式f(x)=(x-2)ex+a(x-1)2>0化归为x 众生(思路再次受挫):含ex怎化呢? 师:化繁为简,可考虑把ex放缩为简单的式子. 众生:掌声雷动. 师:生9把ex放大为简单的e避免了超越运算,我们为他的机智而喝彩,还有别的放缩方法吗? 师:同学们太了不起了,老师还没看到哪本书刊有这么自然优美的解法,你们发现的解法是原创! 生13:把ex放大为关于a的式子.考虑到f(x)=(x-2)ex+a(x-1)2右边第二项含a,为使右边放缩为积的形式,令ex 师:是啊,可以考虑一般的情形. 生15(约5分钟思考与整理):令ex 师:棒极了,又是一种原创! 我还原了高考命题专家的心路历程,我也会高考命题了! 众生:掌声如潮,学生脸上露出前所未有的自信和喜悦. 师:思想方法比知识更重要,请大家总结今天的探究用到哪些数学思想方法. 众生:数形结合、化归与转化、分类与整合、函数与方程、有限与无限、具体与抽象、特殊与一般、分析法、综合法、放缩法、待定系数法、配方法、换元法,… 师:我欣慰的感到同学们逻辑推理,数学运算,直观想象,数学抽象素养在提升. (在掌声和下课铃声中师生说“再见”.此“再见”不仅是礼仪用语更是学生心语,是他们对美好数学探究活动的期盼.) 3.1 自然方能内化 知识的内化如同生理上的消化一样,食物要经过加工烹饪和弯弯曲曲肠道的消化,营养才能被人体吸收.这种消化是曲折的也是自然的.自然的才能内化,内化了方能优效,这是教学不可违背的规律.为使学生的学习能“何由以知其所以然”,教师应对数学文本进行加工和创作,通过教学情境创设和导思探究活动,在一波三折、峰回路转和“山穷水尽疑无路,柳暗花明又一村”的数学思维历程中,引发学生的发现与创造.从而使数学课堂彰显了自然的本色,弥漫着自然的芬芳,让数学教学不是莫名其妙和强加于人.教学要力求自然,要揭示本质,让定义生成自然;展示背景,让概念形成自然;练习巩固,让目标达成自然;创设情境,让问题提出自然;归纳类比,让定理发现自然;探究分析,让解题思路自然;寻求联系,让章节过度自然;一题多变,让习题延伸自然;交流反思,让思想体悟自然. 3.2 导师贵在导思 发展核心素养要求学生应具有理性思维,批判质疑,勇于探究的科学精神.数学教育的根本任务在于发展学生的思维,让学生能用数学的思维分析现实世界.数学课堂的精髓是学生在教师引导下的深度思考.要引发学生的思维,教师要示以学生思维发展之道,课堂要变教为导,变学为思,以导达思,即教师要变为导师,导师贵在导思.课堂上教师创设问题情境,学生思考回答问题,师生对所答问题进行评价修正,引发学生进一步思考.学生思考过程中产生疑惑或思维碰撞或有助于问题解决的想法,教师给于点拨分析引导,学生再尝试探究直至问题解决.教师要能理解学生的思维基础,洞察学生的思维困惑,在思维的循循善诱上下功夫,精心创设思维引导语.导语要顺应学生原有认知结构、思维方式和学习经验,要贴近学生思维最近发展区和思维潜在发展区.导语要呈阶梯式一步一步通向目标,要有一定的思维度,能启迪学生的心智,学生深思熟虑后豁然开朗.教师可通过一系列追问来激活学生的思维,如“解决这类问题有何经验?”“问题是怎样发现的?”“你是怎样想到的?”“式子的形式结构是什么?”“式子有图形背景吗?”“问题的特殊情形是什么?”“问题的一般情形是什么?”“数学(思维)本质是什么?” “能否找到与它相似的问题?”“如何进行化归与转化?”“能否从更广范围看问题?”“还有别的研究视角吗?”“知识背后蕴涵着什么数学思想方法?”等.通过环环相扣,跌宕起伏的导思、探究、领悟、互助,引发了学生思维的自然流泻和灵动创新. [1]刘绍学.普通高中课程标准实验教科书﹒数学1-5必修[M].北京:人民教育出版社,2007. [2]教育部考试中心.2016年普通高等学校招生全国统一考试试题、参考答案[M].福州:福建省教育考试院,2016. *本文系福建省教育科学“十三五”规划2016年度课题“高中数学课堂结课策略的研究”(立项批准号:FjjkxB16—169)的阶段研究成果.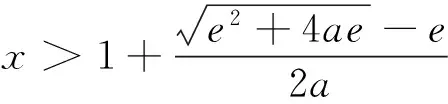
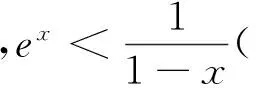
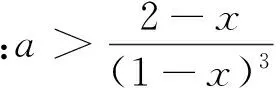

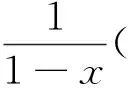
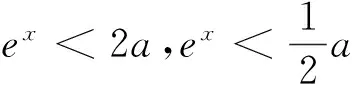
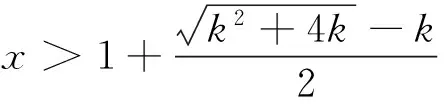
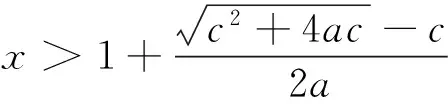
3 教学体悟
