基于励磁调压特性的交流同步电机强励控制*

杜 川， 付会凯

(新乡学院 机电工程学院， 河南 新乡 453003)

基于励磁调压特性的交流同步电机强励控制*

杜 川， 付会凯

(新乡学院 机电工程学院， 河南 新乡 453003)

为了探索励磁调压特性对交流同步电机强励的控制关系，通过励磁EEAC理论从励磁调压角度对交流同步电机的强励控制进行分析，应用Matlab系统建立自并励单机仿真模型，并仿真分析了暂态过程中机端电压对交流同步电机强励的调控关系.结果表明，机端电压决定着电功功率，电磁功率决定着系统暂态稳定的裕度.在忽略损耗的条件下，电功功率等价于电磁功率，因而机端电压决定着励磁系统暂态稳定的裕度.

励磁系统；调压特性；同步电机；强励控制；电磁功率；机端电压；仿真模拟；裕度

励磁系统是交流同步电机的重要组成部分，是发电机和电力系统运行经济性和稳定性的主要评价指标之一[1-3].励磁系统由功率单元和控制单元两部分组成，功率单元主要为发电机提供直流电流形成磁场；控制单元主要调节系统电流，以确保发电机正常状态稳定运行及事故发生时的调节恢复能力.励磁系统基本结构如图1所示.

依据系统电源的不同，励磁系统的励磁方式可分为直流励磁、交流励磁、静态励磁3种[4-7].静态励磁根据电源的构成不同又可分为自并励励磁系统和自复励励磁系统，由于自并励方式具有响应速度快、机端电压稳定、振荡抑制能力强、短路电流衰减小、运行可靠性高等优点[8-11]，因而被广泛应用于大型发电机中.强励是保证发电机

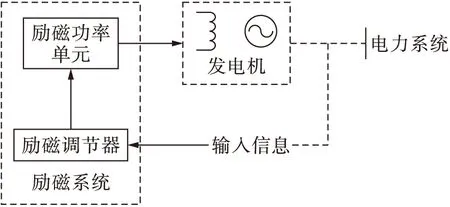
图1 发电机励磁控制系统结构Fig.1 Structure of excitation control system of generator

系统稳定的重要措施，目前国内外很多学者研究了强励电流对励磁系统的影响，强励电流响应时间越短，发电机系统的稳定性越高，然而转子回路的时间常数制约强励电流的响应时间，进而影响着发电机系统的稳定性[12].励磁强励动作的正确性对电力系统的稳定性具有重要作用，由于其调控比较复杂，在使用过程中仍存在着许多问题亟待解决，对于交流同步电机强励控制的分析还存在许多局限性.本文依据扩展等面积准则(EEAC)及功率守恒原理推导出机端电压与强励控制的关联关系，同时以单机无穷大电网系统中励磁电压的阶跃扰动信号来仿真强励过程，在Matlab软件Simulink平台的SPB中建立常规PID励磁控制系统仿真模型，分析了暂态过程中机端电压对强励的控制，为励磁调压特性对强励过程的调控提供理论依据.

1 励磁调压对强励的控制

励磁系统强励控制是电力系统通过调节输出的无功功率来调控发电机的机端电压及并网电压，以维持电力系统的稳定性，避免系统电压大幅度跌落，以及促进电力系统遭受短路时电压的恢复.在发电机系统运行过程中，负荷电流的变化是引起机端电压变化的主要因素，通常用电机的调压静差率来表示，即当发电机系统中自动励磁调节器的调差单元退出时，电压的给定值保持不变，系统负载从额定功率减小到零时机端电压的变化率，以此来评价励磁系统维持机端电压稳定的能力.一般来说，发电机在系统运行过程中引起机端电压变化的主要因素为负荷电流的变化，即负荷电流的变化会引起电磁功率的变化.当电磁功率从零变化到额定功率的过程中，环境温度、频率、电源电压波动的变化会引起机端电压的变化，进而实现对励磁强励的控制.

1.1 强励控制与电磁功率的关系

依据扩展等面积准则，发电机在并网运行时遭受大的扰动后，系统中所有发电机将被分为临界s群和余下a群，整个系统可被等值为一个时变的单机无穷大系统，系统中的广义惯性时间常数与转子角的乘积等于系统机械功率与电磁功率之差，即

Mδ=Pm-Pe

(1)

(2)

δ=δs-δa

(3)

(4)

(5)

式中：M为广义的惯性时间常数；δ为转子角；Pm为机械功率；Pe为电磁功率.

根据功率守恒原理，在忽略网损功率的条件下，s群的电磁功率Pes等于s群和a群之间所有有功功率之和，即

Pes=PLs+Pas+Pdc

(6)

式中：PLs为s群有功功率；Pas为s、a群之间交流有功功率；Pdc为s、a群之间直流有功功率.

a群的电磁功率Pea等于a群内部的有功功率与s、a群之间交流及直流线路的有功功率之差，即

Pea=PLa-Pas-Pdc

(7)

对于独立的电力系统来说，系统的稳定性与系统暂态稳定裕度η(t)密切相关，稳定裕度可表示为

(8)

由式(1)～(8)推算可知，在采取强励控制后，等值系统电磁功率的提升量ΔPe和系统稳定裕度的提升量Δη的表达式分别为

(9)

(10)

由式(9)、(10)可以看出，当励磁系统强励的控制作用ΔPe>0时，励磁系统的正摆稳定性得到改善，反摆稳定性则被恶化；当励磁系统强励的控制作用ΔPe<0时，则反之.由此可知，励磁强励是励磁系统通过改变电力系统的电磁功率ΔPe，进而来调控电力系统运行的稳定性.

1.2 电磁功率与机端电压的关系

根据机械功率守恒原理可知，发电机轴上输入的机械功率P1等于机械损耗PΩ、定子铁耗PFe以及转变为旋转磁场和电磁感应作用的电磁功率Pe之和，即

P1=PΩ+PFe+Pe

(11)

电磁功率Pe等于电枢铜耗PCua与输出功率P2之和，即

(12)

式中：m为电机数量；Ra为电枢电阻；φ为相位角.从而可知Pe=mI2Ra+mUIcosφ=mI(IRa+Ucosφ).发电机各向量关系如图2所示，依据图2进行分解可得IRa+Ucosφ=E0cosψ0，即Pe=mE0Icosψ0.

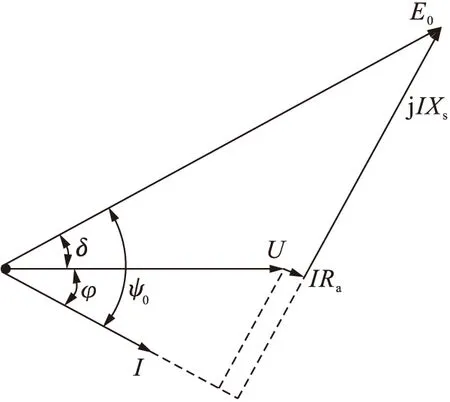
图2 发电机向量关系Fig.2 Vector relationship for generator

以隐极机为例，忽略电阻损耗，此时电磁功率等于输出功率，即Pe=P2=mE0Icosψ0，则其向量关系图如图3所示.斜三角形中向量Icosψ0=(Usinδ)/Xs，从而得出

(13)

式中，Xs为电机电抗.当激磁电动势E0和输出转子角δ恒定时，机端电压U对电磁功率Pe起着决定作用，Pe随着U的变化而变化.

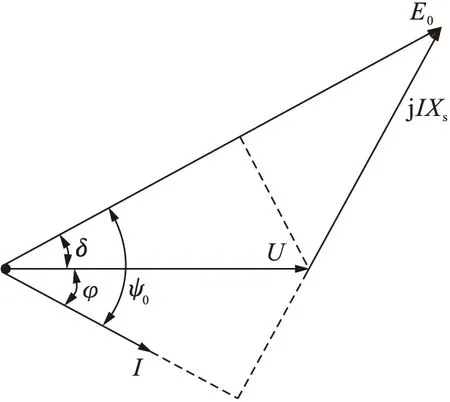
图3 发电机简化向量关系Fig.3 Simplified vector relationship for generator

由式(10)、(13)可知

(14)

由此可知机端电压U对磁励系统的强励进行了调控.

2 仿真及结果分析

应用计算机仿真软件对电力系统建立仿真模型，可有效预测电力系统的安全性、可靠性和精准性，也可为电力系统的安全稳定运行提供可靠保障.为了保证所研究的问题具有普遍性特征，应用软件对典型的单机无穷大母线电力系统进行仿真，同时设定供给的机械功率恒定不变，且忽略电动机功率损耗.本文应用Matlab软件Simulink平台建立的常规PID励磁控制系统仿真模型如图4所示，即在Matlab环境下的自并励励磁单机无穷大母线仿真模型.

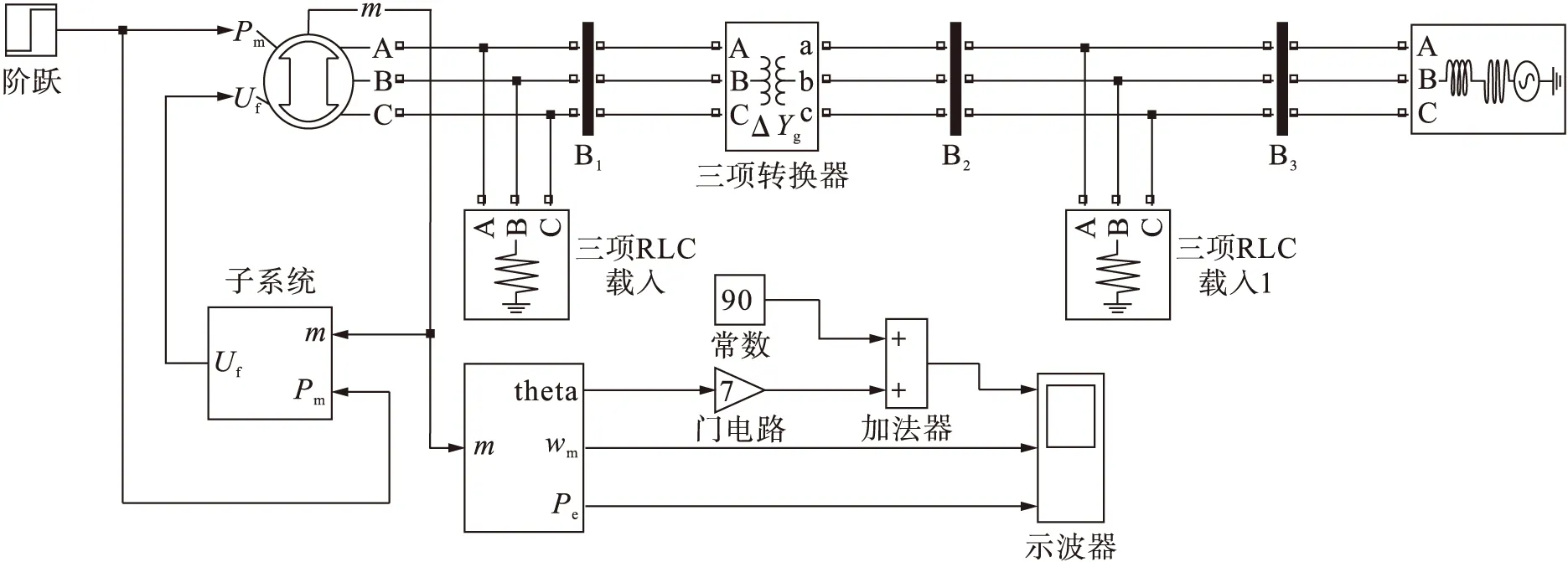
图4 自并励励磁控制系统仿真模型Fig.4 Simulation model for self-excited excitation system

仿真模型的参数设定：电机容量P=250 MVA，额定电压U=13.5 kV，频率f=50 Hz，纵轴电抗之和Xd=1.853 Ω，横轴电抗之和Xq=0.717 Ω，漏电抗Xl=0.16 Ω，短路时电流瞬时变化时间td1=1.05 s，超瞬时变化时间为td2=0.055 s，谐波补偿时间tb=0 s、tc=0 s，积分控制器的比例系数Ka=100、积分系数Ta=0.008.在建立的仿真模型中，当t=10 s时，给励磁系统励磁控制器的机端电压输入端加上10%的阶跃扰动信号进行模拟仿真，图5～7分别为发电机电磁功率、转速和励磁电压在扰动条件下的仿真曲线，横坐标为时间，纵坐标分别是对应的标幺值.在t=10 s设置单机无穷大系统发生三相短路，且在10.2 s时将短路故障切除，图8、9分别是发电机电磁功率和转速的仿真曲线.从以上仿真图可以看出，该系统具有较好的动态调节性能和较强的抗干扰能力.

图5 机端电压阶跃扰动电磁功率仿真曲线Fig.5 Simulation curve for electric power under step disturbance of terminal voltage

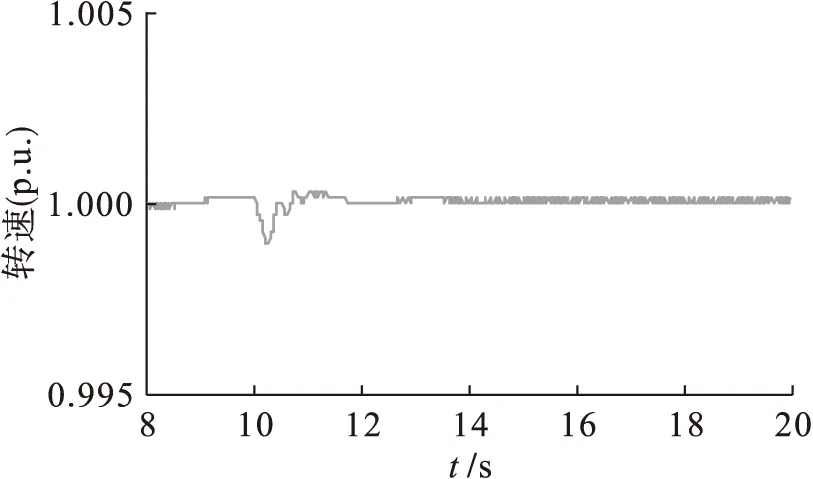
图6 机端电压阶跃扰动转速仿真曲线Fig.6 Simulation curve for rotational speed under step disturbance of terminal voltage

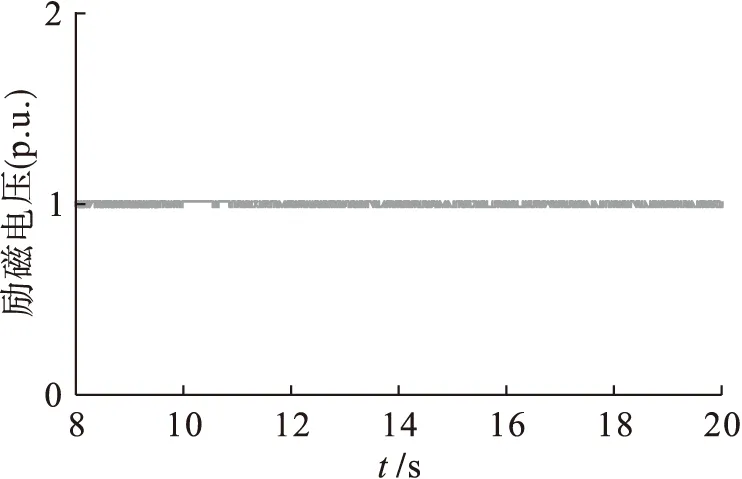
图7 机端电压阶跃扰动励磁电压仿真曲线Fig.7 Simulation curve for excitation voltage under step disturbance of terminal voltage

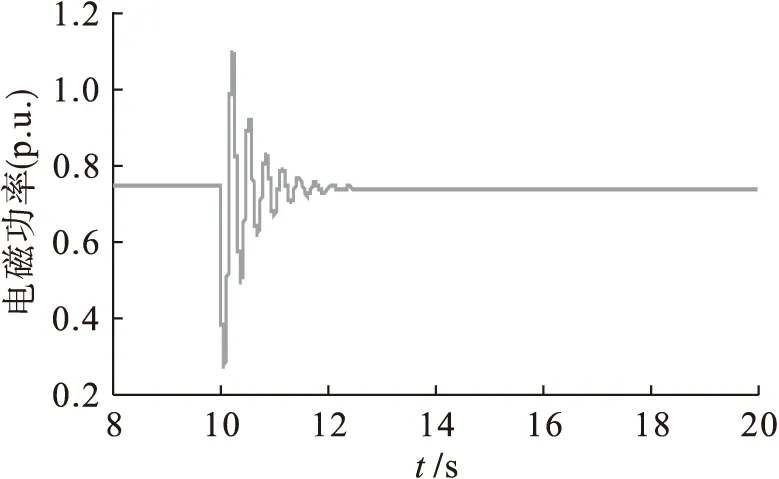
图8 三相短路阶跃扰动电磁功率仿真曲线Fig.8 Simulation curve for electric power under step disturbance of three phase short circuit

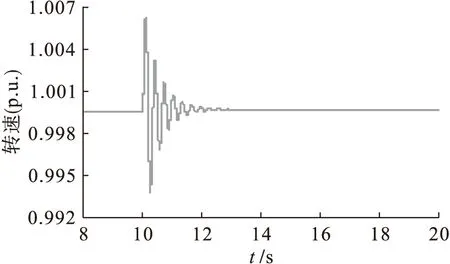
图9 三相短路阶跃扰动转速仿真曲线Fig.9 Simulation curve for rotational speed under step disturbance of three phase short circuit

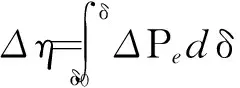
3 结 论

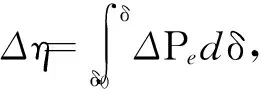
[1]杜治，马蕊，梁易乐，等.一种发电机励磁系统模型参数可辨识性分析方法 [J].电力系统保护与控制，2014，42(22)：38-44.

(DU Zhi，MA Rui，LIANG Yi-le，et al.Analysis method on parameter identifiability for excitation system model of generator [J].Power System Protection and Control，2014，42(22)：38-44.)

[2]李兆伟，周旭，刘昱辰，等.自备电厂发电机励磁系统稳定性分析及控制研究 [J].电力系统保护与控制，2014，42(10)：8-14.

(LI Zhao-wei，ZHOU Xu，LIU Yu-chen，et al.Analysis and control for captive generator excitation system stability [J].Power System Protection and Control，2014，42(10)：8-14.)

[3]毛承雄，何金平，王丹，等.全控器件励磁系统的多变量反馈线性化控制 [J].中国电机工程学报，2013，33(22)：53-60.

(MAO Cheng-xiong，HE Jin-ping，WANG Dan，et al.Multivariable feedback linearization scheme for new excitation systems based on full controlled devices [J].Proceedings of the CSEE，2013，33(22)：53-60.)

[4]张振，徐科军，杨双龙，等.具有快速响应的电磁流量计高低压励磁系统 [J].电子测量与仪器学报，2013，27(6)：562-571.

(ZHANG Zhen，XU Ke-jun，YANG Shuang-long，et al.High and low voltage excitation system with high speed response for electromagnetic flow-meter [J].Journal of Electronic Measurement and Instrument，2013，27(6)：562-571.)

[5]Masmoudi D A.Design of a brushless excitation system utilizing pot cores [J].Journal of Computations and Mathematics in Electrical，2015，34(6)：1740-1757.

[6]张虹，徐滨，高健，等.基于最小方差基准的励磁系统性能评估 [J].电力系统保护与控制，2014，42(8)：54-58.

(ZHANG Hong，XU Bin，GAO Jian，et al.Perfor-mance assessment of excitation system based on minimum variance benchmark [J].Power System Protec-tion and Control，2014，42(8)：54-58.)

[7]Taniguchi T，Kondou T.373 elucidation of operating mechanism of dynamic absorber for parametric excitation system：stability analysis based on complex model analysis [J].International Journal of Molecular Sciences，2015，16(5)：11785-11803.

[8]谢丹.静止自并励励磁系统的设计方案的探讨 [J].电力建设，2003，24(12)：32-34.

(XIE Dan.Inquisition into design scheme of exciting system with static self parallel excitation [J].Electric Power Construction，2003，24(12)：32-34.)

[9]陈利芳，陈天禄.浅谈自并励励磁系统在大容量机组中的应用 [J].继电器，2007，35(1)：81-84.

(CHEN Li-fang，CHEN Tian-lu.Application of self-excitation mode in large capacity generator unit [J].Relay，2007，35(1)：81-84.)

[10]张栩，彭志炜，邱国跃，等.自并励静态励磁系统自动电压调节器参数对暂态稳定性的影响仿真 [J].大电机技术，2013(4)：56-60.

(ZHANG Xu，PENG Zhi-wei，QIU Guo-yue，et al.Influence of AVR parameters of static excitation system on transient stability [J].Large Electric Machine and Hydraulic Turbine，2013(4)：56-60.)

[11]刘振武，魏建忠，高仕斌.自并励发电机后备保护改进方案 [J].电力系统及其自动化学报，2013，25(2)：53-57.

(LIU Zhen-wu，WEI Jian-zhong，GAO Shi-bin.Improved scheme of backup protection for generators with self-shunt excitation [J].Proceedings of the CSU-EPSA，2013，25(2)：53-57.)

[12]许强.基于恒励磁电流的同步电动机强励方法 [J].河北工业科技，2012，29(6)：499-501.

(XU Qiang.A reinforced excitation method based on the constant excitation current of synchronous motor [J].Hebei Journal of Industrial Science and Techno-logy，2012，29(6)：499-501.)

(责任编辑：景 勇 英文审校：尹淑英)

Forced excitation control of AC synchronous motor based on excitation regulation characteristics

DU Chuan,FU Hui-kai

(School of Mechanical and Electrical Engineering,Xinxiang College,Xinxiang 453003,China)

In order to explore the relationship of excitation voltage regulation characteristics to the forced excitation control of AC synchronous motor,the forced excitation of AC synchronous motor was analyzed from the point of excitation voltage regulation through the excitation EEAC theory.The simulation model for the self-excited single motor was established with Matlab system.In addition,the regulation relationship of terminal voltage to the forced excitation of AC synchronous motor in the transient process was simulated and analyzed.The results show that the terminal voltage determines the electric power,and the electromagnetic power determines the margin of system transient stability.Under the condition of ignoring the loss,the electric power is equivalent to the electromagnetic power,and thus the terminal voltage determines the margin of excitation system transient stability.

excitation system;voltage regulation characteristic;synchronous machine;forced excitation control;electromagnetic power;terminal voltage;analogue simulation;margin

2016-06-27.

河南省高等学校重点科研资助项目(168470003).

杜 川(1982-)，男，河南新乡人，讲师，硕士，主要从事电气控制、电力传动等方面的研究.

22 17∶40在中国知网优先数字出版.

http：∥www.cnki.net/kcms/detail/21.1189.T.20161222.1740.022.html

10.7688/j.issn.1000-1646.2017.02.02

TM 315

A

1000-1646(2017)02-0127-05