基于多特征降维的植物叶片识别方法

郑一力 钟刚亮,2 王 强,2 赵 玥 赵燕东

(1.北京林业大学工学院， 北京 100083; 2.中国科学院电工研究所， 北京 100190)

基于多特征降维的植物叶片识别方法

郑一力1钟刚亮1,2王 强1,2赵 玥1赵燕东1

(1.北京林业大学工学院， 北京 100083; 2.中国科学院电工研究所， 北京 100190)

植物种类识别方法主要是根据叶片低维特征进行自动化鉴定。针对低维特征不能全面描述叶片信息，识别准确率低的问题，提出一种基于多特征降维的植物叶片识别方法。首先通过数字图像处理技术对植物叶片彩色样本图像进行预处理，获得去除颜色、虫洞、叶柄和背景的叶片二值图像、灰度图像和纹理图像。然后对二值图像提取几何特征和结构特征，对灰度图像提取Hu不变矩特征、灰度共生矩阵特征、局部二值模式特征和Gabor特征，对纹理图像提取分形维数，共得到2 183维特征参数。再采用主成分分析与线性评判分析相结合的方法对叶片多特征进行特征降维，将叶片高维特征数据降到低维空间。降维后的训练样本特征数据使用支持向量机分类器进行训练。试验结果表明：使用训练后的支持向量机分类器对Flavia数据库和ICL数据库的测试叶片样本进行分类识别，平均正确识别率分别为92.52%、89.97%，有效提高了植物叶片识别的正确率。

叶片识别； 多特征降维； 主成分分析； 线性评判分析； 支持向量机

引言

植物的种类识别是植物学研究和农业生产的基础性工作，传统方法主要是根据植物形态进行人工鉴定，识别结果存在主观性且效率较低。植物叶片含有大量种属信息，且大部分叶片外形为扁平状，因此可对植物叶片进行图像采集和处理，实现植物种属快速识别。

目前，大多数研究采用少量特征描述因子对植物叶片进行分类识别。20世纪80年代，INGROUILLE等[1]提取叶片的27个形状特征，使用主分量分析方法对橡树进行分类研究。王晓峰等[2]提取植物叶片的矩形度、圆形度和偏心率等8个几何特征参数和7个图像不变矩，应用移动中心超球分类器对20多种植物叶片进行分类识别，平均正确识别率达到92%。NETO等[3]使用傅里叶描述因子对植物叶片进行描述，采用判别式分析对4种植物分类，平均正确识别率为89.4%。姚宇飞[4]使用8个几何特征、7个Hu不变矩特征、1个结构特征、4个灰度共生矩阵特征和1个分形维数特征共21维特征描述叶片样本，并使用主成分分析对特征进行降维，使用支持向量机对26种植物进行识别试验，平均识别率为91.54%。DU等[5]计算叶片边缘和多层纹理的二维分形维数，并提取一种新的环形投影小波分形特征，采用K最近邻(k-nearest neighbor, k-NN)分类器对30种植物叶片图像进行分类实验，正确识别率为87.14%。KULKARN等[6]提取植物叶片的形状特征、静脉特征、颜色特征与纹理特征，用径向基概率神经网络对32种植物进行分类，平均正确识别率为93.82%。HERDIYENI等[7]利用半径为2、邻域像素点为16的局部二值模式算子对植物叶片样本进行编码并采用概率神经网络进行分类识别，正确识别率为78.89%。杜吉祥等[8]采用5个尺度、6个角度的Gabor滤波器对叶片样本进行滤波，然后对各滤波子图计算均值和方差作为子图特征，再利用新型的径向基概率神经网络模型对50类植物进行分类识别实验，正确识别率为84.4%。LE等[9]提出一种新的基于内核描述的方法用于植物叶片识别，然后用SVM分类器对Flavia数据库和ImageClef 2013数据库进行分类识别实验，正确识别率分别为97.5%和58.0%。ZHAO等[10]用2个局部描述因子和3个新的三角形表达方式对叶片进行描述，然后用k-NN对Image-CLEF 2011叶片进行分类识别实验，成功识别率最高为89.79%。刘念等[11]用Hu氏不变量、傅里叶描述子、局部二值模式、Gabor滤波和灰度共生矩阵多特征对植物叶片进行描述，获得较高的识别结果，但由于提取特征维度较高，对分类器有较高要求。

植物种类繁多，少量的特征描述因子不能详细描述叶片信息，导致形状和纹理相似的植物叶片不容易被区分开。提取高维特征描述植物叶片时，所需的分类器算法复杂，增加识别难度。

本文给出一种基于多特征降维的植物叶片识别方法。该方法主要提取叶片图像的形状特征和纹理特征作为叶片多特征。叶片形状特征包括叶片几何特征、不变矩特征和结构特征，叶片纹理特征包括灰度共生矩阵特征、分形维数、局部二值模式特征和Gabor特征。然后使用主成分分析和线性评判分析对叶片多特征进行特征降维，构成叶片特征数据库。最后通过支持向量机对训练样本的叶片特征数据库进行训练，实现对植物叶片的快速分类识别。

1 图像预处理

叶片颜色一般随着生长季节变化，叶片虫洞会影响叶片特征提取，以上两种因素均会干扰叶片识别结果。此外，叶片的叶柄长度、直径无一定规律，在叶片识别中为无用信息。为削弱叶片数字图像中颜色、叶柄、虫洞等无用或干扰信息，使目标区域特征更明显，本文先对输入的叶片彩色图像进行旋转处理，使叶片长轴与水平方向平行，然后对其进行预处理。预处理的输出为用于叶片多特征提取的叶片灰度图像、二值图像和纹理图像，具体过程如图1所示。

图1 叶片图像预处理流程图Fig.1 Flow chart of image preprocessing

首先，将输入的叶片彩色图像经灰度转换得到原始灰度图像，利用最大类间方差法对其进行阈值分割处理，将叶片从背景中提取出来，得到叶片的原始二值图像。采用形态学中的开运算和闭运算对原始二值图像进行处理，可得到不受颜色、虫洞和叶柄影响的叶片二值图像。

然后，将二值图像矩阵和原始灰度图像矩阵进行点乘运算，得到去除背景的叶片灰度图像。

用HSI(Hue saturation intensity)色彩空间模型的S分量(饱和度)表示叶片纹理。在提取纹理图像时，首先将叶片彩色图像转换为HSI色彩空间下的图像[12]，然后用S分量图像矩阵与二值图像矩阵进行点乘计算，得到去除数字图像背景的叶片纹理图像。

2 多特征提取

采用多特征对植物叶片进行全面描述，叶片多特征包括叶片形状特征和叶片纹理特征。

2.1 形状特征

同类的植物叶片形状具有一定的规则性，对其进行分析可以得到能有效描述叶片形状的特征参数。本文叶片形状特征由叶片几何特征、叶片不变矩特征和叶片结构特征等表示。

2.1.1 几何特征

在叶片二值图像中提取叶片的纵横轴比、矩形度、球状性、圆形度、偏心率、周长凹凸比、面积凹凸比和形状参数8个无量纲的量[2]描述植物叶片几何特征，这些几何特征不受植物生长影响。

2.1.2 Hu不变矩特征

HU[13]提出的不变矩具有旋转、平移和尺度不变性特性，故采用CHEN[14]改进的针对离散对象的不变矩算法，在叶片灰度图像的基础上计算得到7个Hu不变矩参数。

2.1.3 结构特征

本文采用锯齿度ST反映叶片结构特征，定义为

(1)

式中NS——锯齿个数P——叶片周长

NS是由SHI等[15]用Shi-Tomasi算法对叶片二值图像进行计算获得的。

2.2 纹理特征

叶片的纹理特征是一种全局特征，对叶片图像整体纹理分析时表现出一定的规则性，本文采用灰度共生矩阵特征、分形维数特征、局部二值模式特征和Gabor特征来描述叶片纹理特征。

2.2.1 灰度共生矩阵特征

灰度共生矩阵(Gray level co-occurrence matrix, GLCM)可以反映图像中任意两点灰度值的空间相关性，采用灰度共生矩阵的对比度、相关性、能量和均匀度4个统计量[16]反映叶片图像纹理特征。本文在灰度图像基础上计算得到4个共生矩阵特征参数。

2.2.2 分形维度特征

植物叶片各层级脉络将叶片分割成具有一定自相似性的网状结构，可用分形维度DF更细致描述叶片纹理特征。

将图1中获取的叶片纹理图像看作点集Z∈R3，每个元素z∈Z被定义为三维坐标值(x,y,Y(x,y))。其中，x,y是空间域中像素的位置，Y(x,y)是对应像素点的灰度。叶片的分形维度DF的计算采用PELEG等[17]提出的“毯子法”。

2.2.3 局部二值模式特征

局部二值模式(Local binary pattern，LBP)[18]是一种用于描述纹理特征的算子。由于LBP算子具有计算简单、旋转不变性和灰度平移不变性等优点，故用于植物叶片的纹理特征提取。

叶片数字图像中任意中间像素点与p个邻域像素点的LBP算子编码方法为

(2)

其中U(Lp,R)=|s(Yp-1-Yc)-s(Y0-Yc)|+

(3)

式中Yc——中间像素点的灰度s——符号函数，当参数为正数或零时，函数为1，否则为0

Yi——以Yc为中心、R为半径的圆上p个邻域像素的灰度

上标为riu2的LBP算子表示旋转不变统一模式，该模式的种类数为p+2。

计算叶片图像LBP参数时，为弱化图像背景对特征提取的影响，将叶片图像缩放至400像素×400像素。首先，提取出灰度图像中叶片的最小包围盒，然后将包围盒长边缩放为400像素，短边按比例变化后，用零填充空白处到400像素。本文采取半径为2、邻域像素数为16的旋转不变统一模式LBP算子对植物叶片灰度图像进行编码，得到叶片LBP编码图，在图中，叶片的边缘和纹理等特征模式均被刻画出来，如图2所示。

图2 LBP编码图Fig.2 LBP coding image

然后将叶片LBP编码图均匀地分为7×7块，统计每一块编码图的直方图，得到叶片子图像的直方图特征。为增大叶片纹理对识别的贡献，减弱叶片背景对识别的影响，将每个子图像的直方图特征乘以相应的权值，叶片编码模式直方图的权值模板如图3所示，最终得到882维(7×7×(16+2))叶片图像LBP特征。

图3 权值模板图Fig.3 Diagram of weight template

2.2.4 Gabor特征

由于Gabor滤波器能同时在频率域和空间域得到最优局部化，具有优良的方向选择性和空间局部性，可用于植物叶片的纹理检测[19]。

二维的Gabor滤波器可以定义为由高斯函数调制的复正弦函数，定义[20]为

(4)

其中

(5)

式中x0——旋转后的复正弦函数横坐标y0——旋转后的复正弦函数纵坐标θ——复正弦函数的旋转角度，用来控制Gabor小波的方向

w0——复正弦函数频率

σ——Gaussian函数沿2个坐标轴标准方差

植物叶片的灰度图像Y(x,y)与G(x0,y0,θ,w0)的卷积定义为

F(x0,y0,θ,w0)=Y(x,y)*G(x0,y0,θ,w0)

(6)

计算叶片图像Gabor参数时，采用与计算LBP相同的缩放方法将叶片图像缩放至400像素×400像素。本文使用5个尺度、8个方向的Gabor滤波器对叶片图像进行滤波，得到40个子图像，得到的子图像如图4所示。

图4 Gabor子图像Fig.4 Gabor sub-images

将每个子图像分成4×4的子块，在每个子块的基础上，计算各子块滤波能量值的方差和均值，最后得到1 280(5×8×4×4×2)维叶片图像Gabor特征。

本文从叶片图像上提取8个几何特征参数(GC)，7个Hu不变矩参数(Hu)，1个结构特征参数(SC)，4个灰度共生矩阵特征参数(GLCM)，1个分形维数(FD)，882维局部二值模式特征(LBP)和1 280维Gabor特征(Gabor)来描述叶片的纹理特征，共得到2 183维特征。

3 多特征降维

由于叶片特征维度过高，本文选用主成分分析(PCA)[21]和线性判别分析(LDA)[22]相结合的方法对多特征进行降维处理，将高维特征参数降到低维空间。

3.1 主成分分析

主成分分析是一种找出数据空间中最能表达原始数据的一组向量的方法，能在保存数据主要信息的前提下，将特征数据从高维降到低维。

用向量xi(i=1,2,…,N)表示第i个叶片样本图像的D维特征，先对xi进行归一化处理。在PCA转换计算中，样本均值计算为

(7)

样本图像的协方差C定义为

(8)

其中

(9)

使用奇异值分解(Singular value decomposition，SVD)定理简化计算矩阵X，可以得到XXT的非零特征值λ[23]。根据特征值可以计算出贡献率，通过确定贡献率可以确定降维后特征的维度d。由此得到大小为D×d的变换矩阵Wpca，PCA转换后的叶片图像特征向量yi可以表示为

(10)

3.2 线性评判分析

线性评判分析与主成分分析的差别是能够寻找最能将特征数据进行分类的低维特征，即最小化类内离散度，最大化类间离散度。将LDA运用于本文的降维处理中，有助于叶片的分类识别。

类内散度矩阵Sw和类间散度矩阵Sb在数学上的定义形式为

(11)

式中C——植物种类数Ni——第i种植物的叶片样本数

si,j——第i种植物中第j个叶片样本

μi——第i种植物种类样本的特征平均值

μ——所有植物种类样本的特征平均值

(12)

3.3 主成分分析和线性判别分析相结合

PCA能够大幅度降低原来的多特征维度，但在进行转换时若不区分各类别间的特征，会丢失判别信息。LDA变换是一个提取叶片低维分类特征的有效方法，但是在叶片识别中，当某些植物种类的训练叶片样本过少，而特征维数过高时，矩阵Sw不能满足非奇异矩阵条件，导致LDA降维失败。针对以上2个问题，本文采用将PCA和LDA结合的方法对叶片高维特征进行降维转换，使叶片多特征维度得以大幅度降低，并保留类间的判别信息，本文方法的表达式为

(13)

式中hi——降维后的第i个特征参数

在提取叶片多特征后，对叶片多特征进行降维处理。然后，将降维后的多特征数据进行归一化处理，即

(14)

式中hmin——降维后特征向量的最小值hmax——降维后特征向量的最大值

为了尽可能地保留叶片信息，选取PCA的贡献率为99%。经过PCA降维，叶片特征能够从高维空间大幅度降低到m维的低维空间。本文使用LDA转换的主要目的是将特征数据进行分类。又LDA只能将n类植物的特征数据降低为1到n-1之间的维度，特征数据经过LDA转换后的维度为

(15)

4 分类器构建

支持向量机(SVM)[24]是通过使用核函数将低维空间中的线性不可分特征数据进行非线性转换，映射到高维空间中，从而得到在高维空间中线性可分的特征数据。继而在新的高维空间中确定出最优的分类面。由于SVM具有良好的鲁棒性，可有效解决叶片样本数量少、非线性特征数据和特征维度高等问题，故本文选用SVM分类器进行分类识别。

SVM定义为

(16)

式中ai——Lagrange乘子SV——支持向量集li——输出类别标号b——由叶片训练样本确定的阈值K(xi,x)——核函数

由于径向基核函数(RBKF)是非线性的函数，在SVM分类器训练过程中，能有效减少计算复杂性。因此本文选择径向基函数作为分类器核函数，定义为

(17)

式中δ——核函数扩展常数，该参数决定SVM分类器的预测能力

在实验时需人工确定SVM分类器的gamma函数g和惩罚变量c。c为分类器对误差的宽容度。g定义为

(18)

本文选用Libsvm工具箱[25]在Matlab平台上进行SVM模型构建，工具箱中包括参数寻优的库函数，且支持植物叶片的多分类。建立SVM的分类识别模型时，通过交叉验证法对试验数据库进行参数寻优，可以得到数据库的最佳参数g和c。

本文在建立SVM的分类识别模型时，分别对Flavia和ICL数据库进行参数寻优，得到ICL数据库的最佳参数g为0.007 812 5，最佳参数c为2。Flavia数据库最佳参数g为0.125，最佳参数c为2。

5 实验与结果分析

5.1 数据库

为了评估本文提出的方法，使用由WU等[26]收集的叶片图像Flavia数据库和由中国科学院合肥机械研究所智能计算实验室建立的叶片图像ICL数据库[27]进行实验。

Flavia数据库包含32种植物叶片样本图像，每种植物叶片样本数量最少为50个，最多为77个，共1 907个样本。该数据库中的叶片图像均为白色背景，尺寸均为1 600像素×1 200像素。实验中每种植物采用45个样本进行训练，剩余样本进行测试。

ICL数据库包含220种植物叶片样本，每种样本最少为26个，最多为1 078个。数据库中叶片图像背景为白色，每张图片尺寸不同，一般为200像素×500像素。实验选用样本数量大于50的42种植物进行分类识别实验，其中，每个种类用45个样本训练，剩余的样本进行测试。

5.2 结果分析

用Matlab和C混合编程实现识别算法。用SVM分类器分别在不同的数据库上采用不同特征方法的对比识别实验结果如表1所示。对比实验的特征方法主要有： 21维特征降维方法(GC+Hu+SC+GLCM+FD)、LBP特征降维方法、Gabor特征降维方法以及本文多特征降维方法(GC+Hu+SC+GLCM+FD+LBP+Gabor)。

表1 不同特征组合降维方法的对比识别实验结果Tab.1 Comparison results of different features dimension reduction method

表1结果表明，本文提出的多特征降维方法提取的2 183维特征能更好地描述叶片信息，且在特征降维时保留大部分信息，平均识别正确率提高。由于ICL数据库的叶片样本图像质量比Flavia数据库低，Flavia数据库正确识别率高于ICL数据库。

将本文提出的特征与文献[2，4，7-8]中的特征用SVM分类器对2个数据库进行分类识别实验，并比较识别结果。实验前均将特征数据进行归一化处理，其余实验条件和文献方法一致，文献方法和本文多特征降维方法的识别结果如表2所示。

表2 叶片识别结果Tab.2 Leaf recognition results

从表2可以看出，在2个数据库中，本文方法的平均正确识别率均高于进行比较的文献方法。表明本文提出的多特征降维方法能更详细、全面地描述叶片信息，故能有效识别植物叶片。

表3为每类植物叶片识别结果，由表3可以看出，ICL数据库中识别率最低的3类植物为白蜡(71.63%)、全缘叶栾树(73.08%)和石榴(75.00%)。Flavia数据库中识别率最低的3类植物为香椿(55.00%)、楠木(57.14%)和毛竹(64.29%)。对比2个数据库的识别结果，Flavia数据库中识别率最低的3类植物识别效果比ICL数据的差。为了分析Flavia数据库出现这个结果的原因，对数据库中识别率最低的3类植物识别结果进一步分析。

表4为识别率最低的3种植物识别结果，观察表4可知，毛竹识别正确次数是9次，错误识别成4种植物：罗汉松(2次)、香椿(1次)、夹竹桃(1次)、桃(1次)。香椿识别正确次数是11次，错误识别成2种植物：栾树(8次)、桃(1次)。楠木识别正确次数是4次，错误识别成2种植物：三角枫(2次)、木蓝(1次)。毛竹与罗汉松、香椿、夹竹桃、桃的叶片形状极为相似，而且毛竹叶片很细，由于照片分辨率的原因，叶片图像丢失大部分纹理信息，导致识别错误。香椿与栾树、桃的叶片形状和纹理都很相似。而楠木与木蓝、三角枫的纹理相似，但锯齿数目有较大差别，而实验中锯齿度参数只有1维，占多特征参数的权值比例小，而且Flavia数据库中大部分叶片锯齿数目差别不大，导致锯齿度这一特征对识别的贡献较小，导致正确识别率低，需进一步强化此类特征的描述。

表3 每类植物叶片识别结果Tab.3 Recognition results of each species

s采用不同特征组合降维方法对500个叶片测试样本进行识别，所需平均时长如表5所示。由表5可以看出，采用本文多特征降维方法，算法复杂度和数据处理量增加，每张叶片图像的平均识别时间增至550.1 ms，可满足叶片识别快速性的要求。

表4 3种植物识别结果

Tab.4 Recognition results of three species

表5 不同特征组合降维方法的识别时间Tab.5 Average recognition time of experiments by using different features

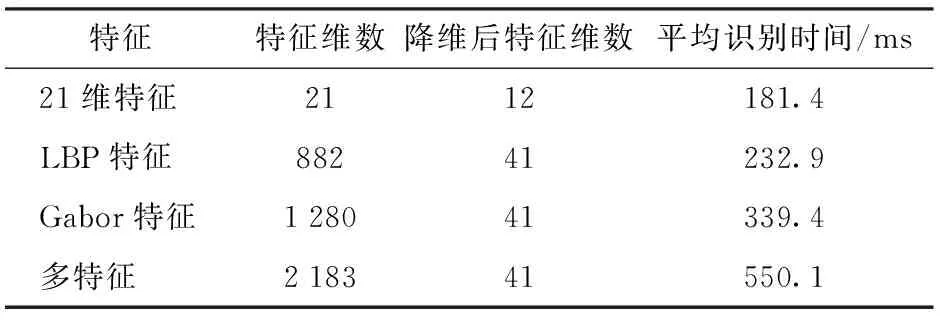
特征特征维数降维后特征维数平均识别时间/ms21维特征2112181.4LBP特征88241232.9Gabor特征128041339.4多特征218341550.1

6 结束语

提出了一种基于多特征降维的植物种类叶片图像识别方法。提取植物叶片的2 183维特征后，采用PCA与LDA相结合的方法进行多特征降维，再使用SVM分类器分别在ICL数据库和Flavia数据库上进行分类识别实验。结果表明，本文提出的多特征降维方法可有效快速识别植物叶片。下一步可深入研究纹理特征参数与形状特征各参数的权值比例，以提高纹理特征对叶片识别的贡献。

1 INGROUILLE J M, LAIRD M S. A quantitative approach to oak variability in some north London woodlands[J]. The London Naturalist, 1986,65:35-46.

2 王晓峰, 黄德双, 杜吉祥, 等. 叶片图像特征提取与识别技术的研究[J]. 计算机工程与应用, 2006,42(3):190-193. WANG Xiaofeng, HUANG Deshuang, DU Jixiang, et al. Feature extraction and recognition for leaf images [J]. Computer Engineering & Applications, 2006,42(3):190-193. (in Chinese)

3 NETO J C, MEYER G E, JONES D D, et al. Plant species identification using elliptic Fourier leaf shape analysis[J]. Computers & Electronics in Agriculture, 2006,50(2):121-134.

4 姚宇飞. 基于分形维数的叶片识别方法研究[D]. 北京:北京林业大学, 2011. YAO Yufei. Research on leaves recognition based on fractal dimension [D].Beijing: Beijing Forestry University, 2011. (in Chinese)

5 DU Jixiang, ZHAI Chuanmin, WANG Qingping. Recognition of plant leaf image based on fractal dimension features[J]. Neurocomputing, 2013,116(10):150-156.

6 KULKARN A H, RAI H M, JAHAGIRDAR D K A, et al. A leaf recognition technique for plant classification using RBPNN and zernike moments[J]. Journal of Computer-Mediated Communication, 2013,2(1):984-988.

7 HERDIYENI Y, KUSMANA I. Fusion of local binary patterns features for tropical medicinal plants identification[C]∥International Conference on Advanced Computer Science and Information Systems, 2013:353-357.

8 杜吉祥, 翟传敏. 基于Gabor纹理特征的植物图像识别方法[C]∥第十四届全国图像图形学学术会议, 2008：246-250.

9 LE T L, TRAN D T, PHAM N H. Kernel descriptor based plant leaf identification[C]∥2014 4th International Conference on Image Processing Theory, Tools and Applications, 2014:1-5.

10 ZHAO Zhongqiu, HONG Yan, ZHENG Peng, et al. Plant identification using triangular representation based on salient points and margin points[C]∥IEEE International Conference on Image Processing, 2015:1145-1149.

11 刘念, 阚江明. 基于多特征融合和深度信念网络的植物叶片识别[J]. 北京林业大学学报, 2016,38(3):110-119. LIU Nian, KAN Jiangming. Plant leaf identification based on the multi-feature fusion and deep belief networks method[J]. Journal of Beijing Forestry University, 2016,38(3):110-119. (in Chinese)

12 孙慧贤, 张玉华, 罗飞路. 基于HSI颜色空间的彩色边缘检测方法研究[J]. 光学技术, 2009,35(2):221-224. SUN Huixian, ZHANG Yuhua, LUO Feilu. Color edge detection based on HSI color space [J]. Optical Technique,2009,35(2):221-224. (in Chinese)

13 HU M K. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory, 1962,8(2):179-187.

14 CHEN C C. Improved moment invariants for shape discrimination[J]. Pattern Recognition, 1993,26(5):683-686.

15 SHI J, TOMASI C. Good features to track[C]∥Proceedings of IEEE Conference on Computer Vision & Pattern Recognition, 1994: 593-600.

16 高程程, 惠晓威. 基于灰度共生矩阵的纹理特征提取[J]. 计算机系统应用, 2010,19(6):195-198. GAO Chengcheng, HUI Xiaowei. GLCM-based texture feature extraction[J].Computer Systems & Applications,2010,19(6):195-198. (in Chinese)

17 PELEG S, NAOR J, HARTLEY R, et al. Multiple resolution texture analysis and classification[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1984,6(4):518-523.

19 DAUGMAN J G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters.[J]. Journal of the Optical Society of America A (Optics & Image Science), 1985,2(7):1160-1169.

20 LEE T S. Image representation using 2D Gabor wavelet[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1996,18(10):959-971.

21 TURK M A, PENTLAND A P. Face recognition using eigenfaces[C]∥1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1991:586-591.

22 BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997,19(7):711-720.

23 ANISSA B, NAOUAR B, ARSALANE Z, et al. Face recognition: comparative study between linear and non linear dimensionality reduction methods[C]∥2015 International Conference on Electrical and Information Technologies, 2015:224-228.

24 CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995,20(3):273-297.

25 CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems & Technology, 2011,2(3):389-396.

26 WU S G, BAO F S, XU E Y, et al. A leaf recognition algorithm for plant classification using probabilistic neural network[C]∥2007 IEEE International Symposium on Signal Processing and Information Technology, 2007:11-16.

27 中科院智能计算实验室.中科院智能计算实验室植物叶片数据库[EB/OL].http:∥www.intelengine.cn/dataset.

Method of Leaf Identification Based on Multi-feature Dimension Reduction

ZHENG Yili1ZHONG Gangliang1,2WANG Qiang1,2ZHAO Yue1ZHAO Yandong1

(1.SchoolofTechnology,BeijingForestryUniversity,Beijing100083,China2.InstituteofElectricalEngineering,ChineseAcademyofSciences,Beijing100190,China)

The identification of plant species is an essential part of botanical study and agricultural production. However, low dimension features cannot describe the leaf information. Thus, it cannot differentiate varieties of plants, and the accuracy is low. A method of plant species identification was proposed based on multi-feature dimension reduction. Firstly, color images of plant leaves were preprocessed by the digital image processing technology. The binary image, gray scale image and texture image without the petiole, wormhole and background were obtained after the preprocessing. Secondly, geometric characteristics and structural characteristic were extracted from the binary image. Hu moment invariants features, gray level co-occurrence matrix features, LBP features and Gabor features were extracted from the gray scale image. The fractal dimension was extracted from the texture images and 2 183 features were extracted to describe leaf samples in number. Thirdly, the method of combining principal component analysis (PCA) and linear discriminant analysis (LDA) was adopted to reduce the feature dimension. Then the feature data of training samples was adopted to train the support vector machine classifier. Finally, the support vector machine classifier was used to classify the feature data of test samples. The experiments were carried out on Flavia database and ICL database. The average accuracy was 92.52% and 89.97%, respectively. The experiments showed that the average accuracy of the proposed method was better than that of the compared researches.

leaf recognition; multi-feature dimension reduction; principal component analysis; linear discriminant analysis; support vector machine

10.6041/j.issn.1000-1298.2017.03.004

2016-09-03

2016-12-07

中央高校基本科研业务费专项资金项目(2015ZCQ-GX-04)和北京市科技计划项目(Z161100000916012)

郑一力(1981—)，男，副教授，主要从事林业生态监测和林业工程装备研究，E-mail: zhengyili@bjfu.edu.cn

TP391.41

A

1000-1298(2017)03-0030-08