两挡变速器纯电动汽车传动系统扭转振动特性分析

宋田堂 王汐文 林连华 徐海港 张建武(. 上海交通大学机械与动力工程学院， 上海 0040；. 时风(集团)有限责任公司， 山东 聊城 5800)

两挡变速器纯电动汽车传动系统扭转振动特性分析

宋田堂1王汐文1林连华2徐海港2张建武1
(1. 上海交通大学机械与动力工程学院， 上海 200240；2. 时风(集团)有限责任公司， 山东 聊城 252800)

针对纯电动汽车的扭转振动问题，以某款具有两挡自动变速器的纯电动汽车传动系统为研究对象，根据传动系各部件的动力学方程，建立动力传动系的扭转振动模型，计算并分析传动系的固有特性和模态振型，并通过SIMPACK建立传动系的多体动力学模型进行强迫扭振计算，分析了部分参数对传动系扭振响应的影响，为纯电动汽车降低传动系扭振提供参考。

纯电动汽车 两挡机械式自动变速器 传动系统 扭转振动 多体动力学

0 引言

中国经济的快速发展促进了居民汽车保有量的增长，同时也加剧了能源紧张、环境污染和城市空间拥挤等问题。纯电动汽车具有节能、环保的优势，已成为各大汽车厂商研发的热点。与此同时，消费者对汽车的NVH(noise，vibration，hardness)性能的要求越来越高，汽车动力传动系统的扭转振动对整车NVH品质的贡献率很高[1]，因此对纯电动汽车传动系统的扭振分析具有重要的现实意义。

扭振研究是动力传动系统的基础性研究课题之一，国内外学者都对其进行了相当深入、广泛的研究[2-6]。这些研究大多通过建立不同类型的传动系扭转振动模型，来分析各种因素对传动系统扭转振动的影响。对具有两挡机械式自动变速器(2AMT)的纯电动汽车，传动系统的扭转振动研究较少。本文以某款具有2AMT的纯电动汽车为研究对象，应用精确求解方法，建立动力传动系的扭转振动微分方程，求解并分析传动系的固有特性和模态振型。同时，运用商业化软件SIMPACK建立传动系的多体动力学模型，进行强迫扭转振动分析，找到影响传动系扭转振动的主要因素。

1 电驱动动力传动系统简介

某纯电动汽车采用前置后驱的动力传动方式。如图1所示，该传动系包括驱动电机EM、2AMT、减速器/差速器总成、驱动半轴和车轮等。

图1 某纯电动汽车传动系示意图Fig.1 Transmission map of electric vehicle

与传统的内燃机汽车相比，该电动汽车的电驱动系统有很大变化，主要表现在：

(1) 电机代替内燃机成为传动的动力源；

(2) 省去了离合器和扭转减振器；

(3) 采用了只有两个挡位的自动变速器。

可见该电动汽车的动力传动系统得到了简化，传动效率得到提高。上述改变也使得该传动系统具有了新的特点：

(1) 传动系统总体上表现为一个欠阻尼系统；

(2) 动力总成的质量明显降低；

(3) 电机动态响应更快，而且存在一定的高频转矩波动，冲击和噪声问题突出[7]。

2 动力传动系扭转振动建模

电动汽车的动力传动系统质量和弹性分布很不均匀，因此宜采用多自由度集中质量-弹性离散化近似模型。该动力传动系统的扭转振动动力学模型如图2所示，其中各部件参数如表1所示。其中，JM、J1、J2、J3、J4、Jd1、Jd2、Jt1、Jt2、Jv分别为电机、常啮合主动齿轮、常啮合被动齿轮、Ⅰ/Ⅱ挡主动齿轮、Ⅰ/Ⅱ挡被动齿轮、减速器/差速器总成主动齿轮、减速器/差速器总成被动齿轮、右车轮、左车轮和整车的等效转动惯量；θm、θ1、θ2、θ3、θ4、θd1、θd2、θt1、θt2、θv分别为电机、常啮合主动齿轮、常啮合被动齿轮、Ⅰ/Ⅱ挡主动齿轮、Ⅰ/Ⅱ挡被动齿轮、减速器/差速器总成主动齿轮、减速器/差速器总成被动齿轮、右车轮、左车轮和整车的转动惯量的角位移；k1、k2、k3、k41、k42、k51、k52分别为电机轴、中间轴、传动轴、右半轴、左半轴、右轮胎、左轮胎的扭转刚度，k12、k34、kd分别为常啮合齿轮副、Ⅰ/Ⅱ挡齿轮副、减速器/差速器总成齿轮副的啮合刚度；Tm为电机受到的扭矩。

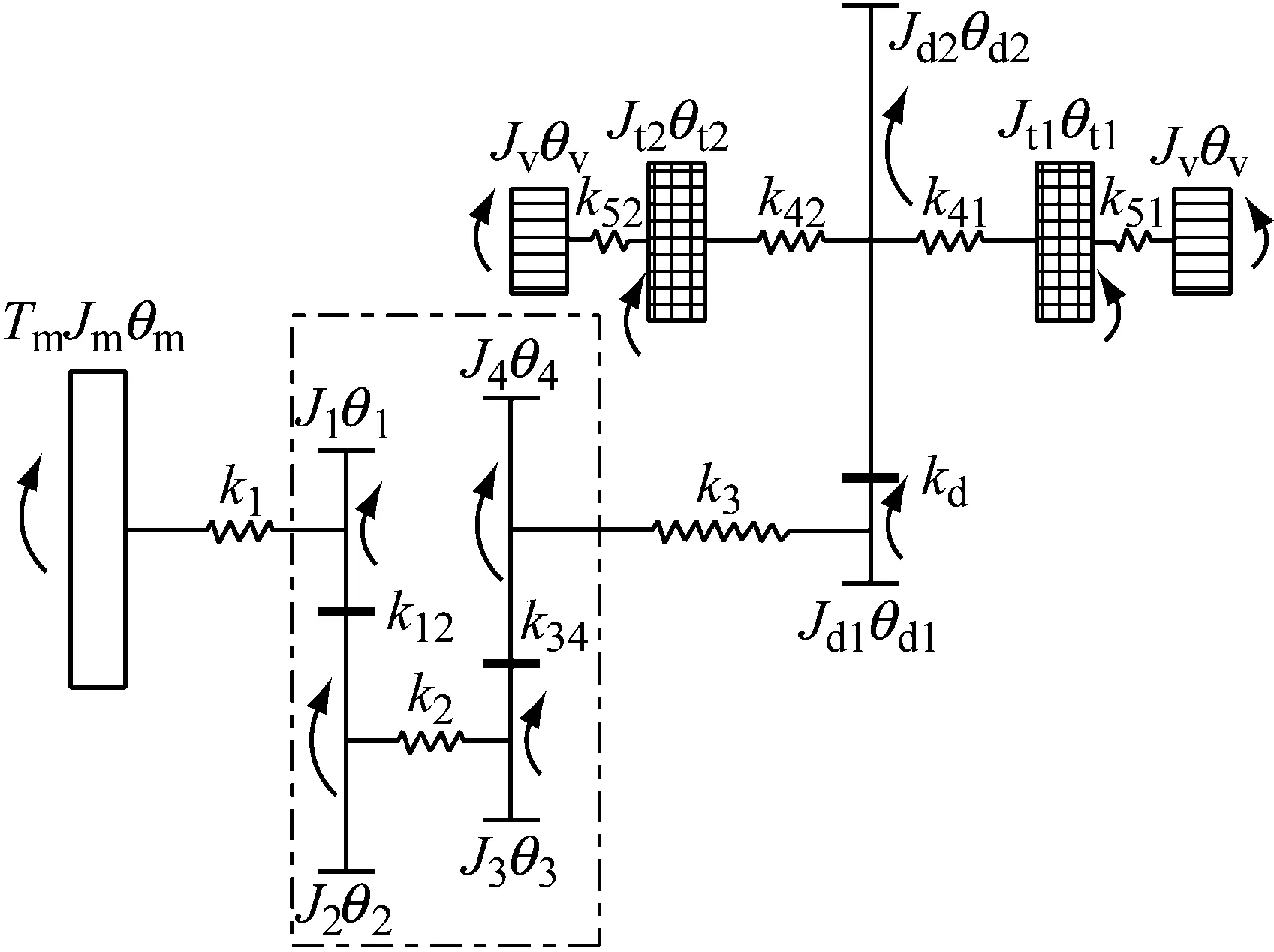
图2 某纯电动汽车传动系扭转动力学模型Fig.2 Dynamic model of vehicle drivetrain

表1 传动系统各部件转动惯量

表2 传动系统各部件扭转刚度

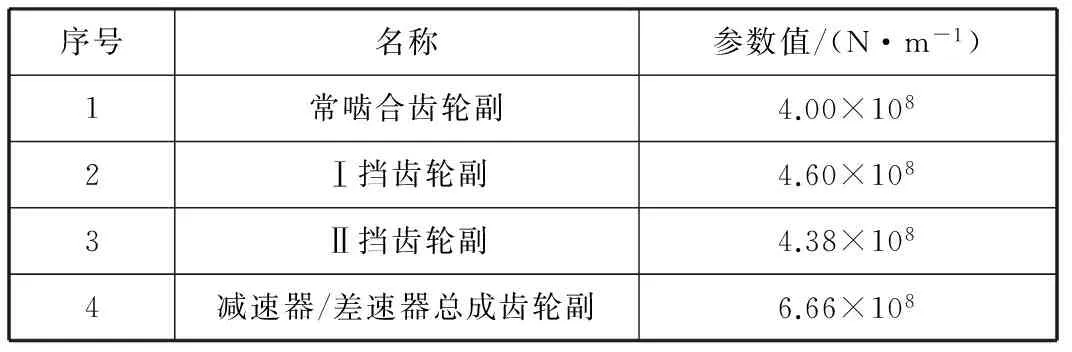
表3 传动系统各部件啮合刚度

由上述动力学模型可列出传动系统各部分的动力学方程，通过各部分动力学方程装配成整体的动力学方程，以此求解传动系统的固有频率及其振型。

电机动力学方程为

(1)

变速器动力学方程为

(2)

(3)

(4)

(5)

式中r1、r2、r3、r4分别为常啮合主动齿轮、常啮合被动齿轮、Ⅰ/Ⅱ挡主动齿轮、Ⅰ/Ⅱ挡被动齿轮的基圆半径。

减速器/差速器总成动力学方程为

(6)

(7)

式中rd1、rd2分别为减速器/差速器总成主动齿轮、减速器/差速器总成被动齿轮的基圆半径。

右车轮和左车轮的动力学方程为

(8)

(9)

整车等效扭转动力学方程为

(10)

通过上述方程(1)-(10)可以整合成系统的特征方程为

(11)

式中M为10×10阶的等效质量矩阵，K为10×10阶的等效刚度矩阵，x为广义位移向量，可表达为

x={θmθ1θ2θ3θ4θd1θd2θt1θt2θv}T

(12)

3 传动系扭振固有特性分析

求解传动系特征方程(11)可得到该传动系的固有频率，每阶固有频率对应的特征向量即为该阶模态振型。在Ⅰ挡和Ⅱ挡时分别计算出的固有频率如表4所示。

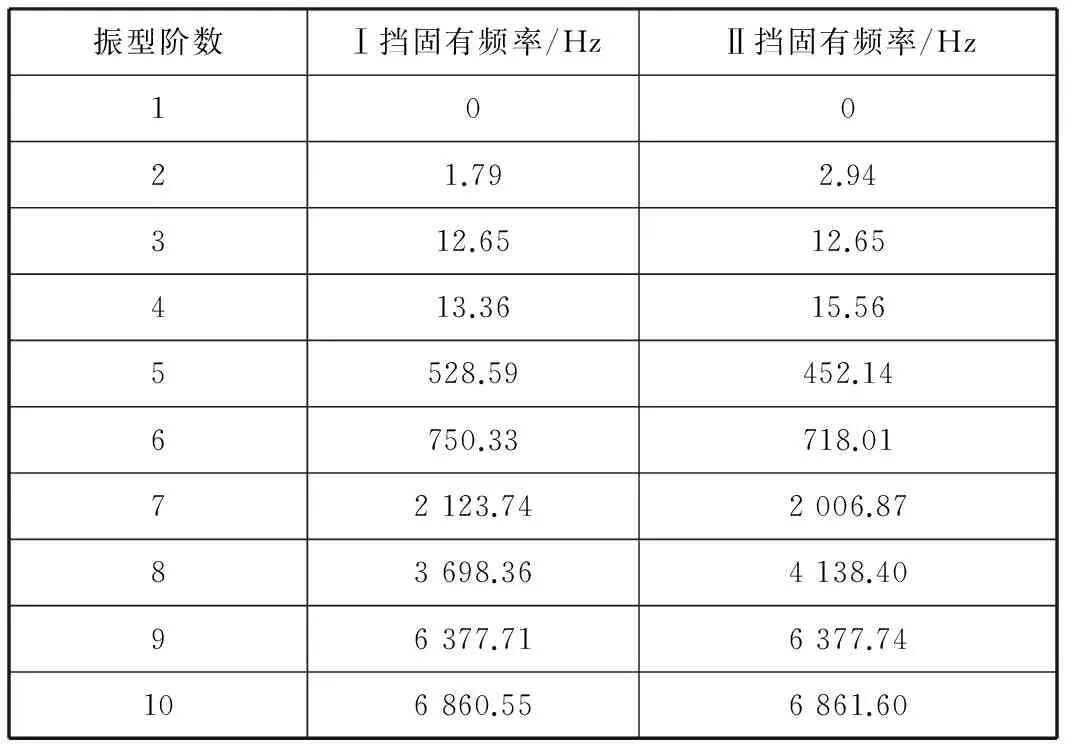
表4 传动系扭转振动固有频率

将模态振型归一化，去除传动比的影响并整合到同一参考系，得到Ⅰ挡时传动系各阶模态振型如图3和图4所示，Ⅱ挡时传动系各阶模态振型如图5和图6所示。

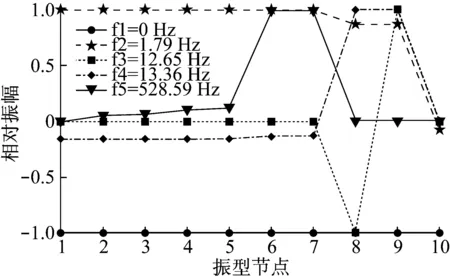
图3 Ⅰ挡时1-5阶振型图Fig.3 Mode shapes 1-5 in first gear

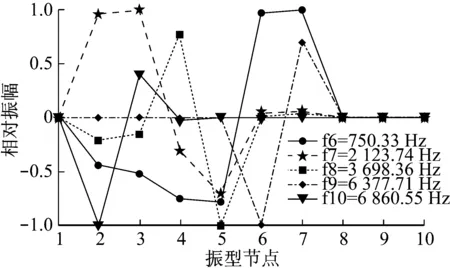
图4 Ⅰ挡时6-10阶振型图Fig.4 Mode shapes 6-10 in first gear

图3和图4中，节点1-10依次为电机、常啮合主动齿轮、常啮合被动齿轮、Ⅰ挡主动齿轮、Ⅰ挡被动齿轮、减速器/差速器总成主动齿轮、减速器/差速器总成被动齿轮、右车轮、左车轮和整车。可以发现，Ⅰ挡时1阶、2阶频率下整车各部件振动都比较明显；3阶、4阶频率接近，车轮处均有明显振动，而且表现出左右车轮反向共振和同向共振两种不同的模态；5阶、6阶频率下减速器/差速器总成主动齿轮和被动齿轮振动明显，Ⅰ挡主动齿轮和被动齿轮处也有较大振动；7阶频率下常啮合主动齿轮和被动齿轮振动明显，Ⅰ挡主动齿轮和被动齿轮处也有较大振动；8阶频率下，Ⅰ挡被动齿轮振动明显，Ⅰ挡主动齿轮处也有较大振动；9阶频率下减速器/差速器总成主动齿轮振动明显，减速器/差速器总成被动齿轮处也有较大振动；10阶频率下常啮合主动齿轮振动明显，常啮合被动处也有较大振动。

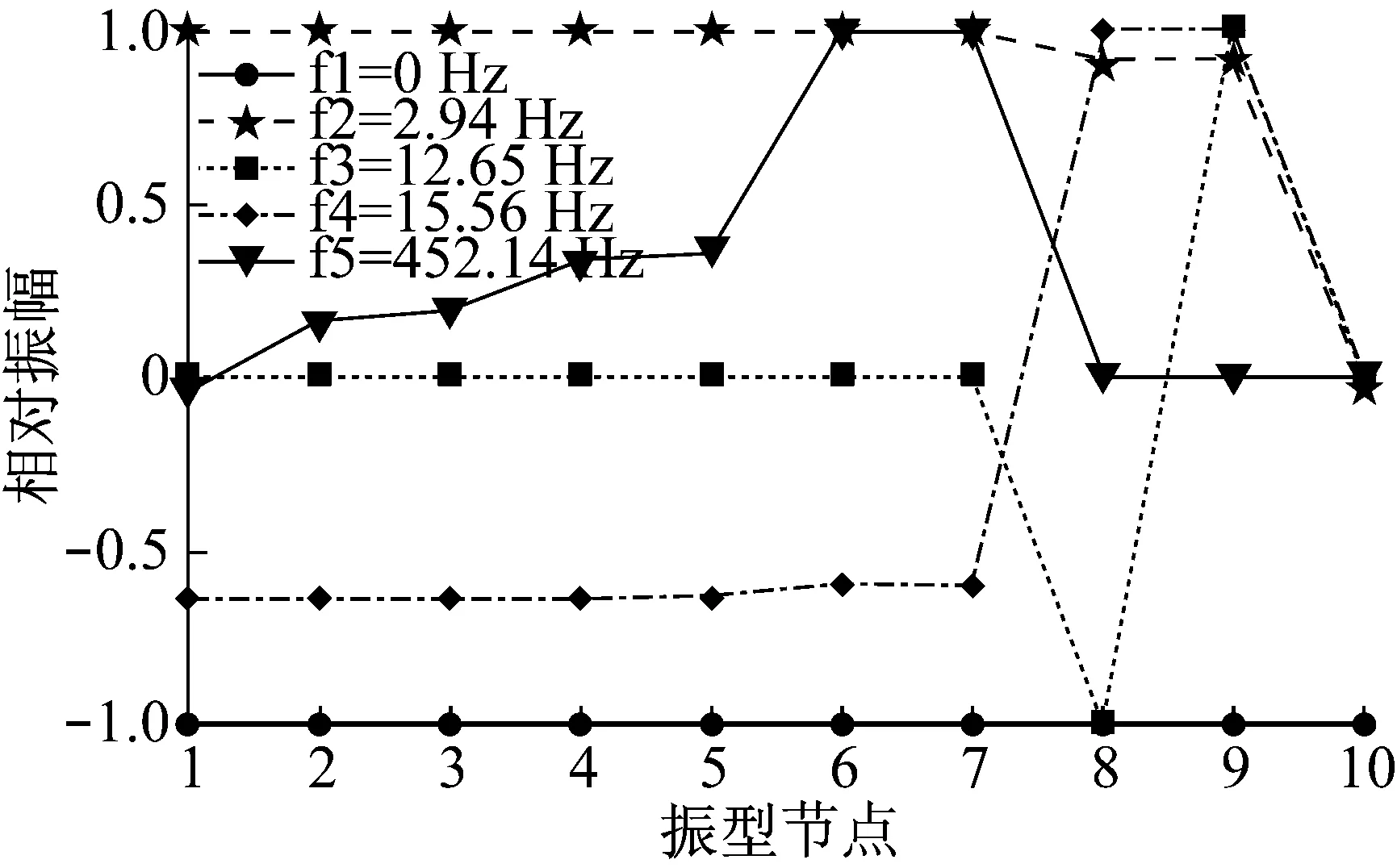
图5 Ⅱ挡时1-5阶振型图Fig.5 Mode shapes 1-5 in second gear

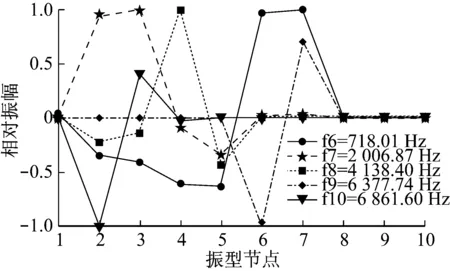
图6 Ⅱ挡时6-10阶振型图Fig.6 Mode shapes 6-10 in second gear

图5和图6中，节点1-10依次为电机、常啮合主动齿轮、常啮合被动齿轮、Ⅱ挡主动齿轮、Ⅱ挡被动齿轮、减速器/差速器总成主动齿轮、减速器/差速器总成被动齿轮、右车轮、左车轮和整车。可以发现，Ⅱ挡时1阶、2阶频率下整车各部件振动都比较明显；3阶、4阶频率下车轮处均有明显振动，而且表现出左右车轮反向共振和同向共振两种不同的模态，但与Ⅰ挡相比，3阶和4阶频率相差略大，且在4阶频率下，除车轮外的各部件也有较大振动；5阶、6阶频率下减速器/差速器总成主动齿轮和被动齿轮振动明显，Ⅱ挡主动齿轮和被动齿轮处也有较大振动；7阶频率下常啮合主动齿轮和被动齿轮振动明显，Ⅱ挡被动齿轮处也有较大振动；8阶频率下，Ⅱ挡主动齿轮振动明显，Ⅱ挡被动齿轮处也有较大振动；9阶频率下减速器/差速器总成主动齿轮振动明显，减速器/差速器总成被动齿轮处也有较大振动；10阶频率下常啮合主动齿轮振动明显，常啮合被动处也有较大振动。

4 传动系强迫扭转振动分析

4.1 SIMPACK动力学模型建立及验证

针对当前2AMT电动汽车的动力传动系统，通过SIMPACK软件和采用多自由度集中质量-弹簧的离散化建模方法，建立多体动力学模型。为了重点分析动力传动系的扭转振动，在SIMPACK建模中作了以下基本假设：

(1) 不考虑弯曲振动和拉压振动；

(2) 忽略传动系中横向、纵向以及垂向振动对扭转振动的影响；

(3) 不考虑附属设备的影响；

(4) 忽略齿轮的变形；

(5) 忽略传动系部件中齿轮安装误差、加工误差和磨损变形。

建立的电动汽车动力传动系SIMPACK模型如图7所示，其中包括EM、2AMT、减速器/差速器总成、驱动半轴、左右车轮和整车等效转动惯量等。

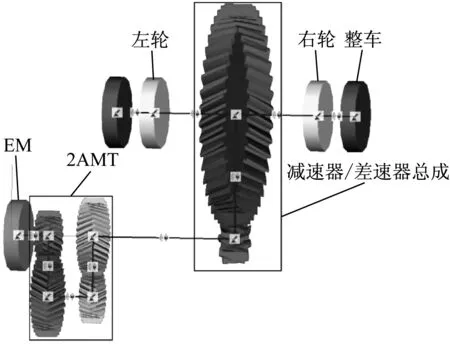
图7 电动汽车动力传动系SIMPACK模型Fig.7 SIMPACK model of vehicle drivetrain

通过SIMPACK动力学模型计算，传动系在Ⅰ挡和Ⅱ挡时的前十阶固有频率由表5和表6给出，为比较起见，同时给出了由微分方程法得出的结果。

由表5和表6可知，两种计算方法得出的Ⅰ挡和Ⅱ挡时的固有频率相对误差都很小，从而相互验证了模型的正确性，说明得到的结果是可靠的。验证结果为进一步对模型进行强迫扭转振动分析打下了基础。

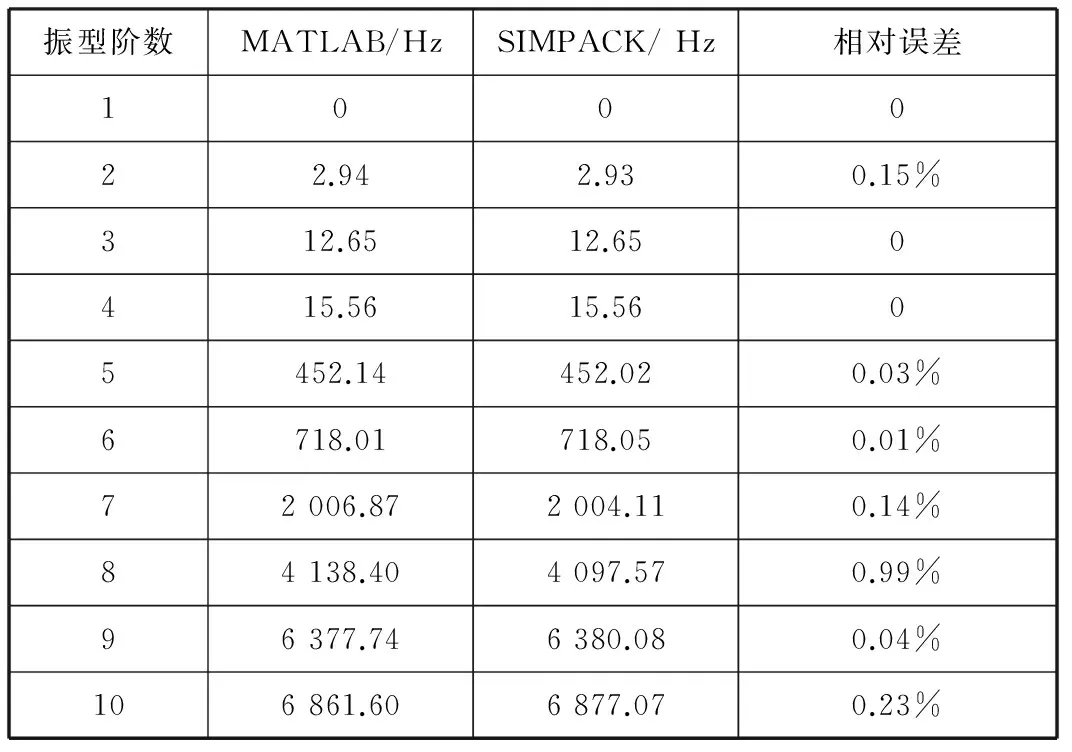
表5 Ⅰ挡时传动系固有频率计算结果比较

表6 Ⅱ挡时传动系固有频率计算结果比较

4.2 动力传动系强迫扭转振动分析

为了分析动力传动系的强迫扭转动力学特性，SIMPACK中在电机端建立输入通道及激振器，使之产生振动激励，该激励为模拟电机产生的输入扭矩；在整车输出端建立输出通道，用以绘制扭振响应的幅值；最后进行强迫扭振的计算设置。通过对不同参数下得到的整车频率响应进行对比，分析和研究影响动力传动系扭振的主要因素。

4.2.1 传动轴刚度和阻尼对扭振的影响

传动轴的扭转刚度为16 104.9 Nm·rad-1，为了研究传动轴刚度对传动系扭振的影响，将传动轴的刚度系数分别取为60%，80%，100%，120%，140%进行仿真计算并比较传动系扭振响应的变化。下面分别讨论Ⅰ挡和Ⅱ挡时，不同传动轴刚度对传动系扭转响应的影响。

由图8可知Ⅰ挡时随着传动轴刚度增加，在1-100 Hz频段的扭转共振幅值没有变化，传动系的低频共振频率也没有变化；在100-1 000 Hz频段的扭转共振幅值变大，传动系的高频共振频率也变大。由图9可知Ⅱ挡时随着传动轴刚度增加，在1-100 Hz频段的扭转共振幅值没有变化，传动系的低频共振频率也没有变化；在100-1 000 Hz频段，传动系的高频共振频率变大，但100-500 Hz频段的扭转共振幅值变大，500-1 000 Hz频段的扭转共振幅值变小。

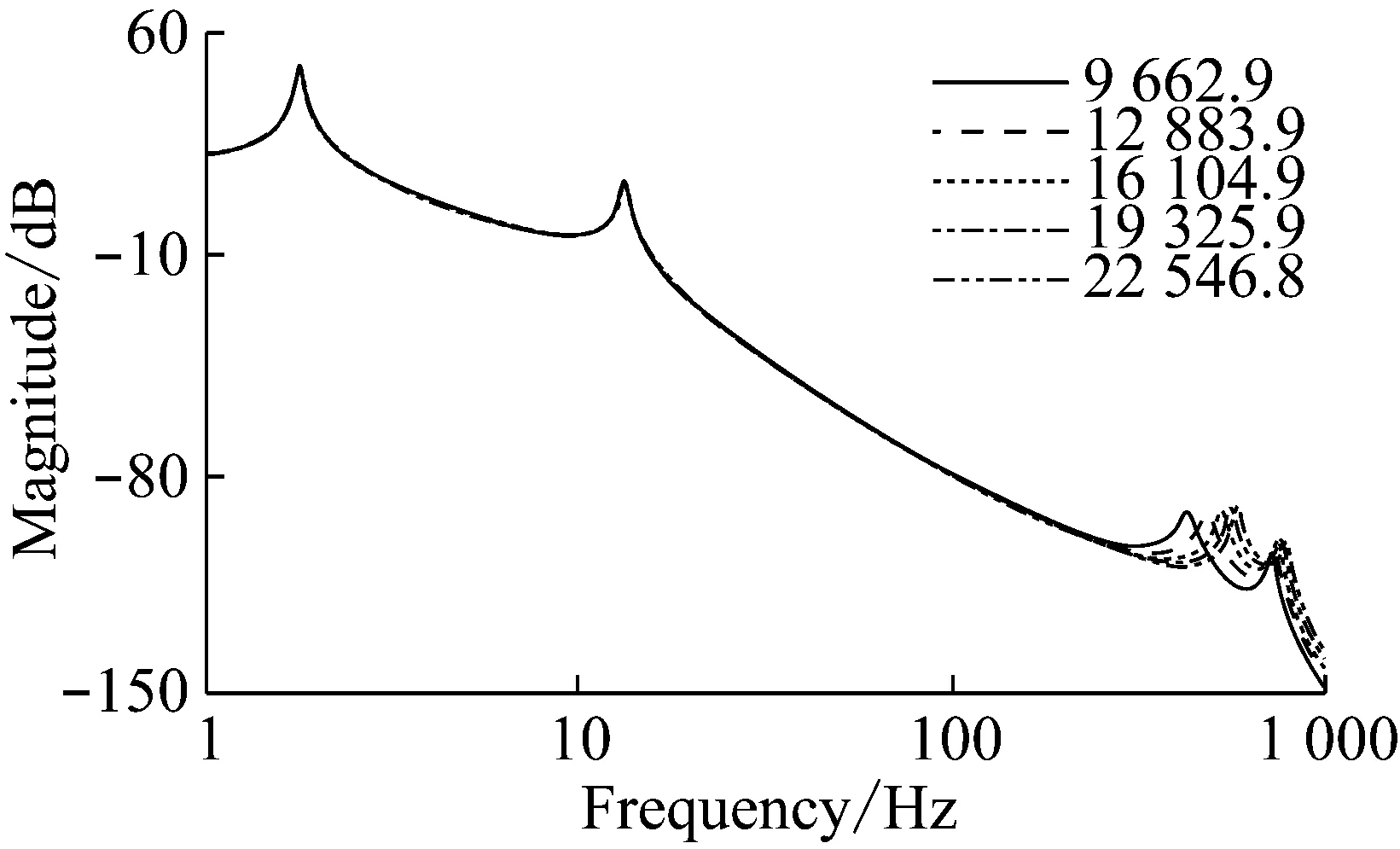
图8 Ⅰ挡时传动轴刚度对传动系扭振的影响Fig.8 Influence on drivetrain torsional vibration through changing drive shaft stiffness in first gear

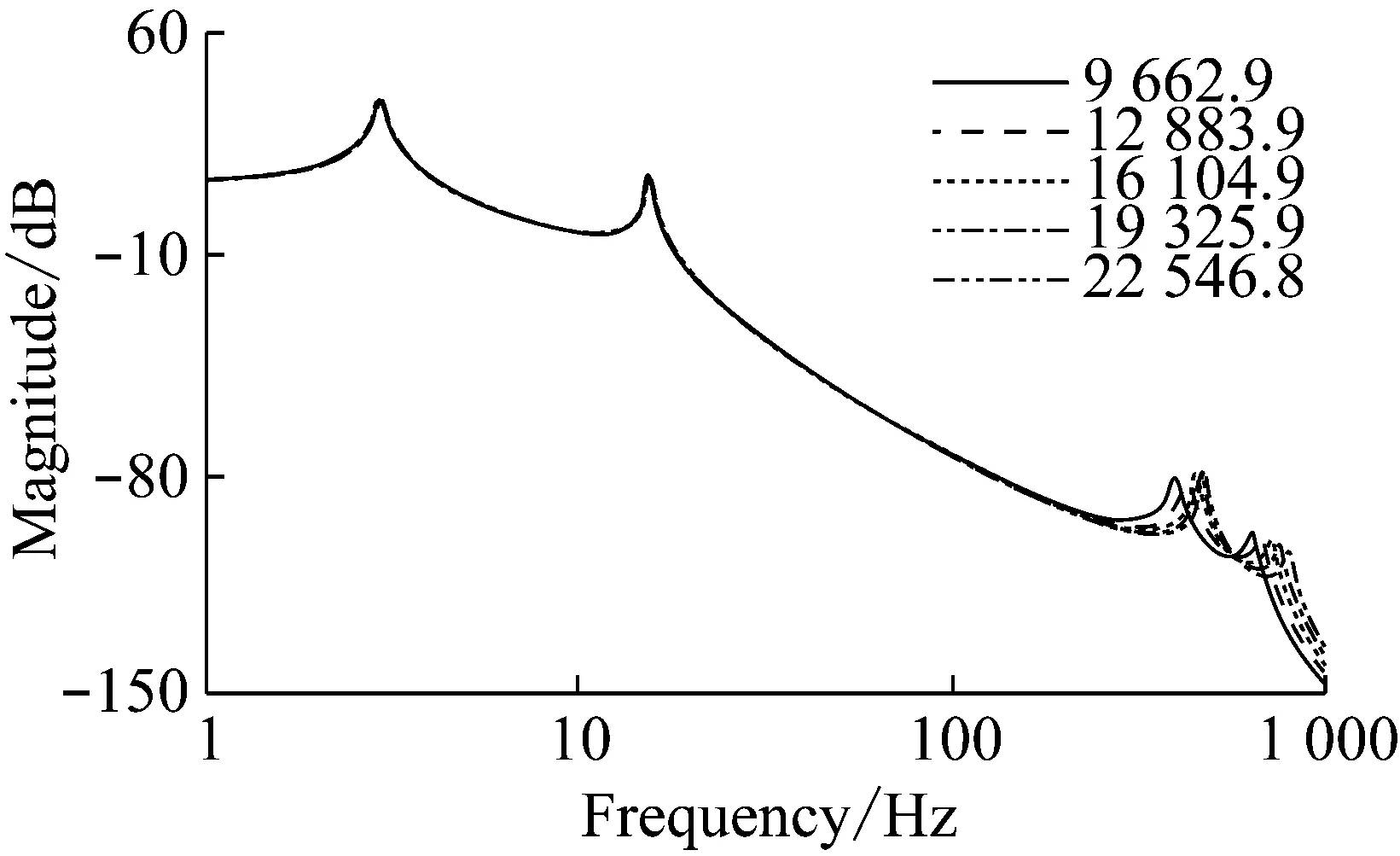
图9 Ⅱ挡时传动轴刚度对传动系扭振的影响Fig.9 Influence on drivetrain torsional vibration through changing drive shaft stiffness in second gear

传动轴的粘性阻尼系数为2.22 Nm·s·rad-1，为了研究传动轴阻尼系数对传动系扭振的影响，将传动轴的阻尼系数分别取为60%，80%，100%，120%，140%进行仿真计算并比较传动系扭振响应的变化。下面分别讨论Ⅰ挡和Ⅱ挡时，不同传动轴阻尼系数对传动系扭转响应的影响。

由图10和图11可知，随着传动轴阻尼系数增加，Ⅰ挡和Ⅱ挡扭振响应相类似，在1-100 Hz频段的扭转共振幅值没有变化，传动系的低频共振频率也没有变化；在100-1 000 Hz频段传动系的扭转共振幅值均会变小，但100-500 Hz频段的扭转共振频率变大，500-1 000 Hz频段的扭转共振频率变小。但相比于刚度系数对传动系扭振的影响，传动轴阻尼系数对传动系扭振的影响很小。

图10 Ⅰ挡时传动轴阻尼系数对传动系扭振的影响Fig.10 Influence on drivetrain torsional vibration through changing drive shaft damping in first gear

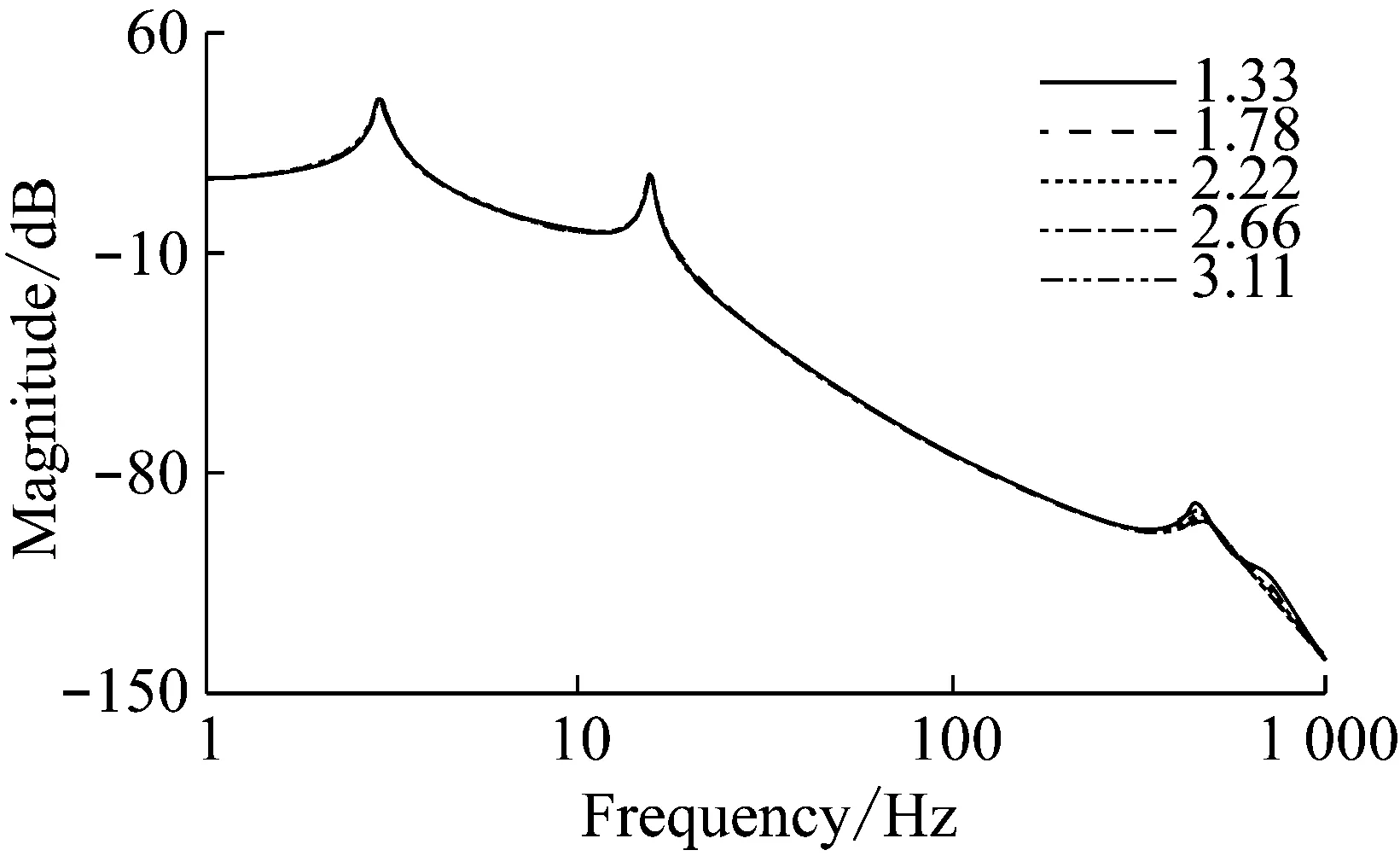
图11 Ⅱ挡时传动轴阻尼系数对传动系扭振的影响Fig.11 Influence on drivetrain torsional vibration through changing drive shaft damping in second gear

4.2.2 半轴刚度和阻尼对扭振的影响

半轴的扭转刚度为5 000 Nm·rad-1，为了研究半轴刚度对传动系扭振的影响，将半轴的刚度系数分别取为60%，80%，100%，120%，140%进行仿真计算并比较传动系扭振响应的变化。下面分别讨论Ⅰ挡和Ⅱ挡时，不同半轴刚度对传动系扭转响应的影响。

由图12和图13可知，随着传动轴刚度增加，Ⅰ挡和Ⅱ挡扭振响应相类似，在1-100 Hz频段的扭转共振幅值略微减小，传动系的低频共振频率变大；100-1 000 Hz频段，传动系的高频共振频率没有变化，但扭转共振幅值变大。增大半轴的刚度能够使传动系的响应幅值变小，可以使乘坐舒适性得到提高。

半轴的粘性阻尼系数为8.29 Nm·s·rad-1，为了研究半轴阻尼系数对传动系扭振的影响，将半轴的阻尼系数分别取为60%，80%，100%，120%，140%进行仿真计算并比较传动系扭振响应的变化。下面分别讨论Ⅰ挡和Ⅱ挡时，不同半轴阻尼系数对传动系扭转响应的影响。

由图14和图15可知，随着半轴阻尼系数增加，Ⅰ挡和Ⅱ挡扭振响应相类似，在1-10 Hz频段的扭转共振幅值没有变化，传动系的低频共振频率也没有变化；在10-100 Hz频段传动系的低频共振频率没有变化，但扭转共振幅值变小；在100-1 000 Hz频段传动系的扭转共振幅值均会变大，但传动系的高频共振频率均会变小。在人体比较敏感的0.5-20 Hz范围内，增加半轴的阻尼，能够降低扭振，也使得乘坐舒适性提高，噪声也得到降低。

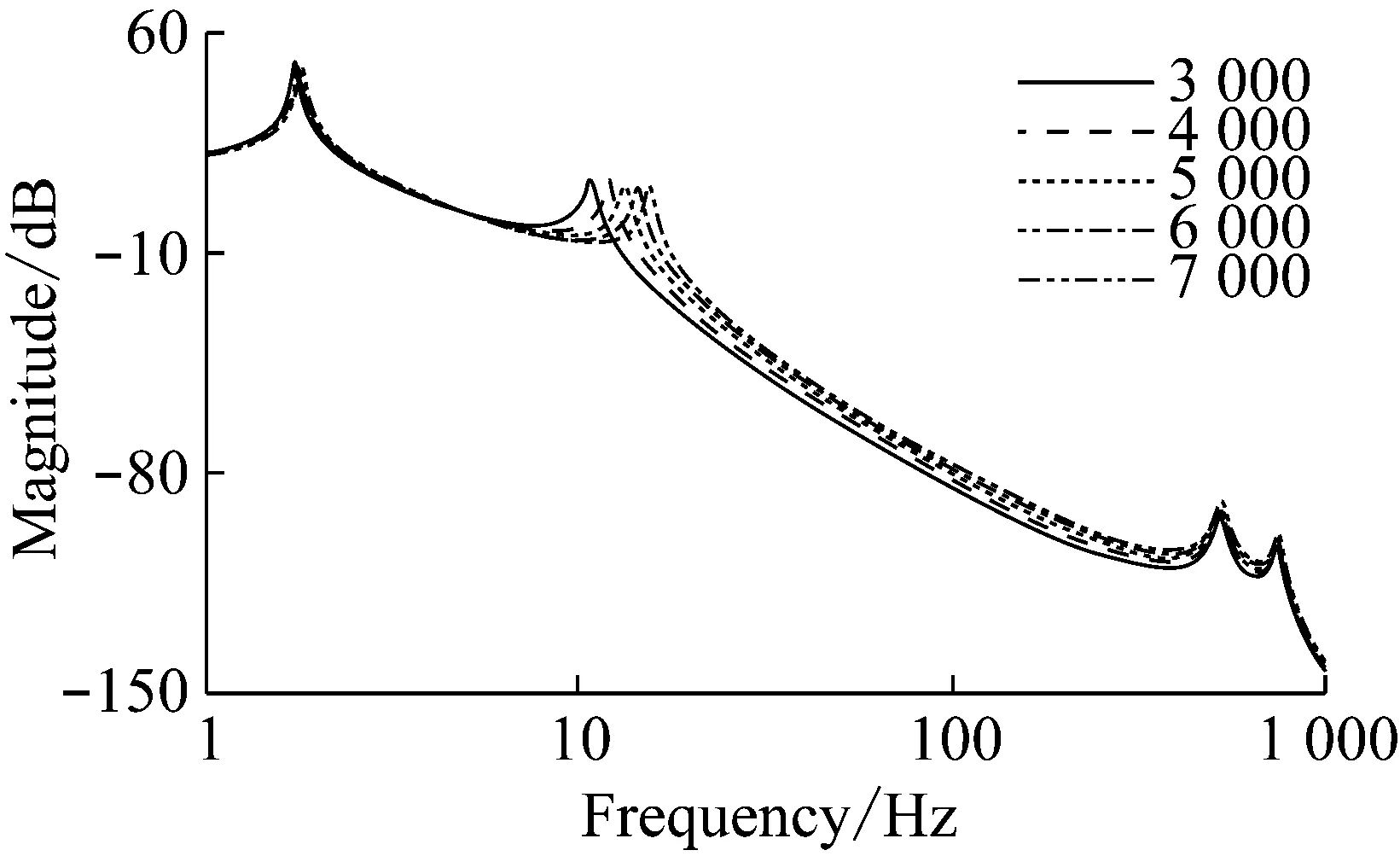
图12 Ⅰ挡时半轴刚度对传动系扭振的影响Fig.12 Influence on drivetrain torsional vibration through changing half-shaft stiffness in first gear

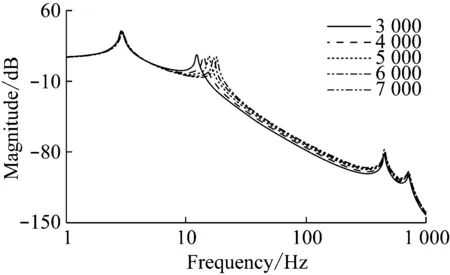
图13 Ⅱ挡时半轴刚度对传动系扭振的影响Fig.13 Influence on drivetrain torsional vibration through changing half-shaft stiffness in second gear

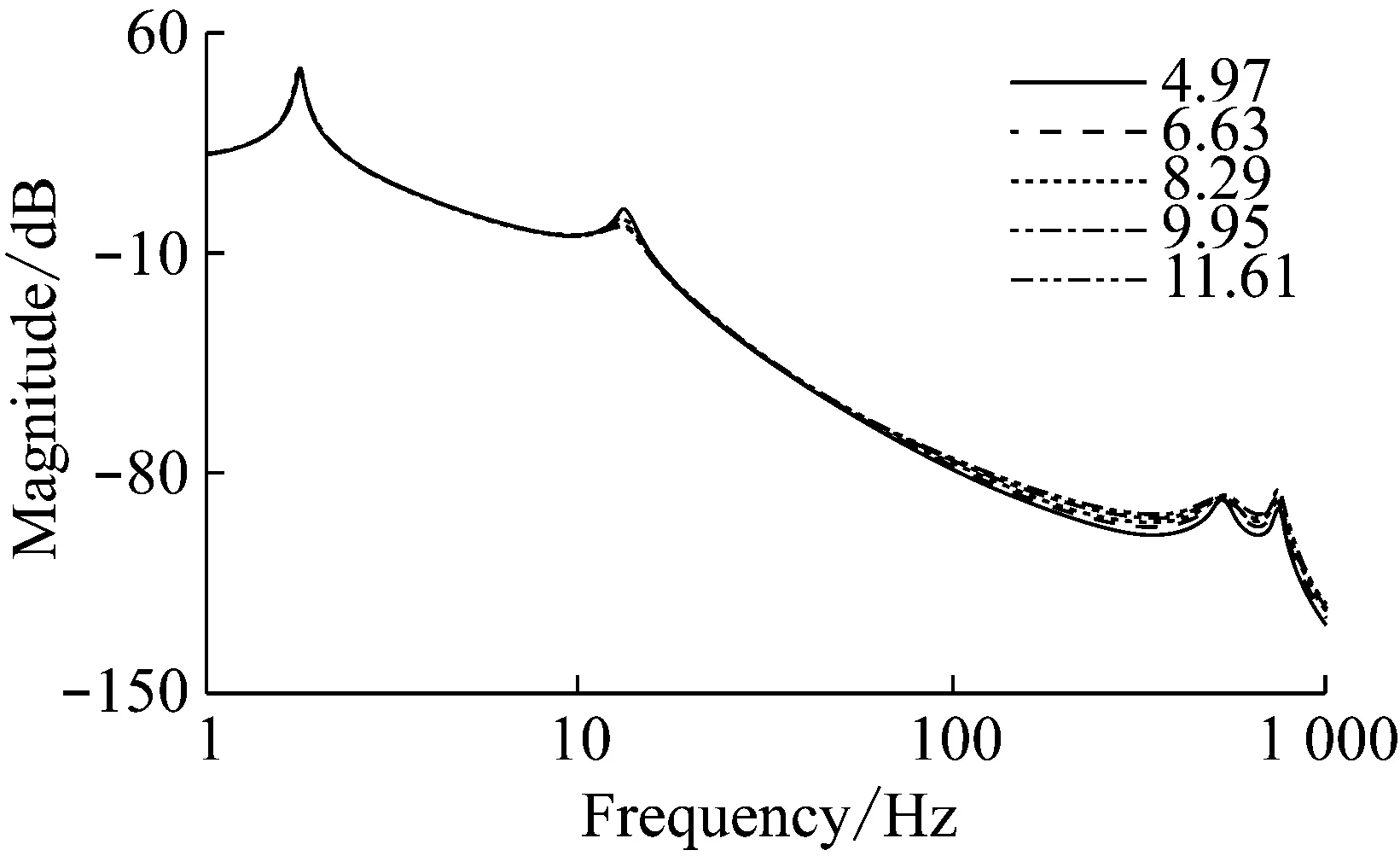
图14 Ⅰ挡时半轴阻尼系数对传动系扭振的影响Fig.14 Influence on drivetrain torsional vibration through changing half-shaft damping in first gear

图15 Ⅱ挡时半轴阻尼系数对传动系扭振的影响Fig.15 Influence on drivetrain torsional vibration through changing half-shaft damping in second gear

4.2.3 电机转动惯量对扭振的影响

电机的转动惯量为0.047 kg·m2，为了研究电机转动惯量对传动系扭振的影响，将电机的转动惯量分别取为60%，80%，100%，120%，140%进行仿真计算并比较传动系扭振响应的变化。下面分别讨论Ⅰ挡和Ⅱ挡时，不同电机的转动惯量对传动系扭转响应的影响。

由图16和图17可知，随着电机转动惯量的增加，Ⅰ挡和Ⅱ挡扭振响应相类似，在1-10 Hz频段的扭转共振幅值变大，但低频共振频率变小；在10-100Hz频段传动系的扭转共振幅值和低频共振频率都在变小；在100-1 000 Hz频段传动系的扭转共振幅值均会变小，传动系的高频共振频率也会变小。

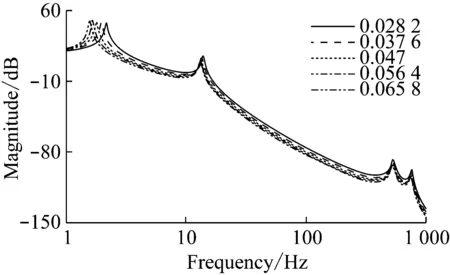
图16 Ⅰ挡时电机转动惯量对传动系扭振的影响Fig.16 Influence on drivetrain torsional vibration through changing rotational inertia of electric motor in first gear

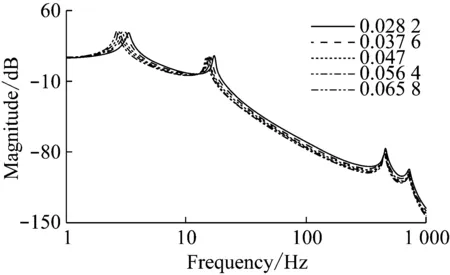
图17 Ⅱ挡时电机转动惯量对传动系扭振的影响Fig.17 Influence on drivetrain torsional vibration through changing rotational inertia of electric motor in second gear

5 结论

(1) 建立了两挡变速器纯电动汽车动力传动系统的动力学模型，列出了传动系各部件的动力学方程，从而进行了传动系扭振固有特性和强迫扭转振动分析。

(2) 动力传动系统的低阶固有频率主要集中在整车和车轮上，中高频集中在变速器常啮合齿轮、Ⅰ/Ⅱ挡齿轮及减速器/差速器总成齿轮上。

(3) 传动轴的扭转刚度和阻尼系数对传动系低频扭振没有影响；半轴的扭转刚度越大，阻尼系数越大，传动系的低频扭振越小，能够提高乘坐舒适性；综合考虑低频段扭振响应，电机的转动惯量取0.047 kg·m2时，传动系扭振响应效果相对较好，从而达到最佳乘坐舒适性。

[1] 庞剑, 谌刚, 何华. 汽车噪声与振动:理论与应用[M]. 北京理工大学出版社, 2006.

[2] Ebrahimi M, Farshidianfar A, Bartlett H. Hybrid Modelling and Simulation of the Torsional Vibration of Vehicle Driveline Systems[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2003, 15(2):217-229.

[3] 于蓬, 章桐. 电机驱动车辆动力传动系统建模方法的研究[J]. 佳木斯大学学报(自然科学版), 2012，(4):498-501.

[4] 邹良, 唐小林, 于海生,等. 混合动力轿车传动系的扭转振动与噪声分析[J]. 汽车工程, 2014，(6):709-714.

[5] 于海生, 张彤, 马智涛,等. 行星排式混合动力汽车传动系扭转振动分析[J]. 农业工程学报, 2013, 29(15):57-64.

[6] 王泽勇, 于蓬, 章桐. 电动车动力传动系扭振模型分支问题研究[J]. 上海汽车, 2013，(3):4-8.

[7] 马琮淦, 左曙光, 杨德良,等. 电动车用永磁同步电机的转矩阶次特征分析[J]. 振动与冲击, 2013, 32(13):81-87.

Analysis of Torsional Vibration Characteristics of Transmission System for Two-speed Electric Vehicle

SongTiantang1WangXiwen1LinLianhua2XuHaigang2ZhangJianwu1
(1.SchoolofMechanicalEngineering，ShanghaiJiaoTongUniversity，Shanghai200240,China； 2.ShifengGroupCompanyLimited，Liaocheng，Shandong252800,China)

This paper focus on the torsional vibration of a two-speed electric vehicle. A simulation model based on the torsional vibration dynamic equation is established to analyze the natural frequencies and mode shapes of the drivetrain. In addition, by using the multi-body dynamics software of SIMPACK, the forced vibration analysis of the drivetrain is carried out to analyze the influence of related parameters on the torsional vibration response, which provides guidance for reducing the torsional vibration of the vehicle drivetrain.

Electric vehicle 2AMT Drivetrain Torsional vibration Multi-body dynamics

*本项目由山东省科技重大专项资助，项目编号(2015ZDXX0601C01)

U463.212

B