基于单因子MSV-CoVaR模型的金融市场风险溢出度量研究
2017-04-19陈九生周孝华
陈九生,周孝华
(重庆大学经济与工商管理学院,重庆 400044)
基于单因子MSV-CoVaR模型的金融市场风险溢出度量研究
陈九生,周孝华
(重庆大学经济与工商管理学院,重庆 400044)
在全球经济一体化进程加速的背景下,信息、资本的自由流动变得更加畅通,金融市场风险从一个市场传向了另一个市场,金融市场风险溢出效应研究也成了金融监管部门以及国内外学者关注的焦点。本文以条件在险价值(CoVaR)法为基础,结合单因子MSV模型分析了我国股票市场与ETF市场之间的风险溢出效应。结果表明,股票市场与ETF市场之间存在双向风险溢出效应,且股票市场对ETF市场的风险溢出效应强于ETF市场对股票市场的风险溢出效应。此外,文章还发现波动冲击对股票市场与ETF市场的影响都较为持久。本文的实证结果能够为投资者在进行股票和ETF投资时提供决策依据,对金融市场监管也有一定的参考价值。
单因子MSV; CoVaR;金融市场;ETF;风险溢出
1 引言
交易型开放式指数证券投资基金(Exchange Traded Funds:ETF)是以拟合某个指数为主的被动式投资基金,被认为是全球金融市场近二十年来最重要的一项金融创新产品。ETF的推出为中小投资者提供了一个方便快捷、灵活及费用低廉的投资渠道,投资者可以用小额资金获得一个多元投资组合的份额,在分散风险的同时也能够获得市场平均收益。ETF还提供了对标的指数的套利功能,一旦出现机会,投资者就能进行大量的套利交易直至ETF价格与指数价值完全一致,这种高频率大量的套利有利于提高标的股票的活跃性,引导资金向蓝筹股集中,并且还能减轻股票指数的波动,保持市场的稳定性。而且,ETF的交易是通过一篮子标的指数的成分股换取一定的基金份额,这种独特的申购和赎回机制决定了即便在一二级市场间进行自身套利也要通过股票市场才能实现。ETF与股票市场的关系如此密切,必然会导致风险从一个市场传递到另一个市场。因此,面对这些收益风险并存的投资工具时,分析股票市场与ETF市场的风险溢出关系不仅能够为投资者在进行股票和ETF投资时提供决策依据,而且还有助于国家对金融行业进行宏观指导,增强决策的有效性。
金融市场间的风险溢出效应一直是国内外学者研究的热门课题也是金融监管部门关注的焦点。现有文献主要是研究国内外股票市场间的风险溢出、股票市场与外汇市场之间的风险溢出、股票市场与整个基金市场以及股票市场与债券市场之间的风险溢出,对于股票市场与ETF基金市场的风险溢出研究较少。Hamao等[1]分析了纽约、东京和伦敦股市之间的价格波动溢出效应,验证了风险溢出效应的存在。洪永淼等[2]研究了A股、B股和H股之间,中国股市与世界其他股票市场之间的极端风险的溢出效应。结果表明,A股、B股与H股之间都存在较强的风险溢出效应,但是,A股与美国、德国和日本等成熟市场国家的股市之间不存在风险溢出效应。刘晓星等[3]也对国际间股票市场之间的风险溢出效应进行了研究,他们认为,美国股票市场对其他国家的股票市场均存在很强的风险溢出效应,并且风险溢出强度还与美国股市自身风险大小成正比。熊正德和韩丽君[4]通过研究我国汇改后汇市与股市间的波动溢出效应,发现股市与汇市之间存在不对称的双向波动溢出效应。史永东、丁伟和袁绍锋[5]研究了股票市场与债券市场的风险溢出效应,结果表明,股票市场与整个债券市场的风险溢出效应不显著,但是股票市场与银行间债券市场存在“跷跷板”效应,并且,股票市场的异常上涨将使“翘翘板”效应变成联动效应;股票市场的异常下跌,“翘翘板”效应会减弱。柏满迎、吴琪和吴天都[6]认为,股票市场和基金市场之间存在风险溢出效应,且股票市场对基金市场的溢出效应要强于基金市场对股票市场的溢出效应。
在研究方法上,目前常用的有风险-Granger因果检验法[7-9]、GARCH类模型法[10-11]、复杂网络模型法[12-13]、CoVaR法[3, 14-15]以及MSV模型法[4, 16-17]。风险-Granger因果检验法和GARCH类模型法能够测度风险的传导方向,但对于风险溢出强度的测量稍显不足。复杂网络模型法能够识别系统重要性金融机构,也能够研究金融体系及风险传导机制,但同样无法测度风险溢出强度。CoVaR法在度量风险溢出强度上应用广泛,但通常需要使用Copula函数作为连接函数,在数据处理过程中容易造成信息损失,而且目前很少有连接函数能够完全拟合两边缘分布。MSV模型中使用较多的是GC-MSV模型和DC-MSV模型,这两种模型也只能测度风险传导的方向,无法度量风险溢出强度。基于此,本文拟结合MSV模型法与CoVaR法的优点,构建单因子MSV-CoVaR模型用于度量金融市场风险溢出。单因子MSV-CoVaR模型不需要使用连接函数也能测度市场间以及机构间的风险溢出强度,对现实的拟合度更高。
2 单因子MSV-CoVaR模型的构建及参数估计
2.1 单因子MSV模型的构建及参数估计
因子MSV模型是借鉴多元分析中的因子分解思想以及因子多元ARCH模型演变而来,它由Harvey等[18]首次提出并经过Jacquier等[19, 20]的扩展和完善。因子MSV模型可以将收益率分解成两个部分:一部分捕捉所有资产定价方面的信息;还有一部分是噪声项(详见Diebold等[21])。
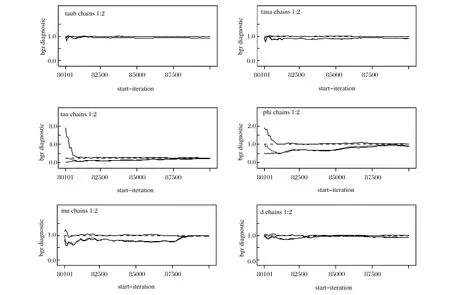
假定ft为K×1维向量,D为m×K维因子载荷矩阵(K (1) 其中,yt=(y1t,y2t)′为t时刻样本数据的收益率序列;D=(1,d)′;εt=(ε1t,ε2t)′为扰动项;ht是标量,h0=0;φ为波动持续项,φ越大,波动的冲击持续性越久;资产收益率序列y1t,y2t之间的条件相关系数为: (2) 单因子MSV模型的参数估计采用基于Gibbs抽样的MCMC方法,参数的先验分布假设根据YuJun和Meyer[22]的经验设为: (3) (4) (5) 其中: (6) (7) pdf(x,y)为二元分布的联合概率密度函数,则ETF基金市场对股票市场的风险溢出为: (8) 表1 ETF基金价格指数及沪深300指数的描述性统计量 注:括号内为P值。 表2 单因子MSV模型的MCMC估计结果 3.1 数据选取 选取沪深300指数代表股票市场,ETF基金价格指数代表ETF市场,样本区间为2010年1月4日至2015年4月30日(数据来源于Wind数据库),以每日收盘价为样本,除去节假日共1289个数据。 首先,对沪深300指数和ETF基金价格指数收盘价进行对数处理,结果用百分比的形式表示。令Rt为第t日的指数收益率,pt和pt-1分别为第t日和第t-1日指数收盘价格,则可用公式表示为: Rt=100×(lnPt-lnPt-1) (9) 其次,将处理好的沪深300指数和ETF基金价格指数收益率进行描述性统计,结果如表1所示。 由表1可知,沪深300指数和ETF基金价格指数收益率的偏度都小于0,峰度都大于3,且J-B检验的P值都为0,所以沪深300指数和ETF基金价格指数收益率序列都不服从正态分布,存在“尖峰、厚尾、左偏”等现象。ADF检验表明,沪深300指数和ETF基金价格指数收益率序列是平稳的,因此,可选用单因子MSV模型进行建模。 图1 单因子MSV模型参数收敛性诊断 图2 单因子MSV模型参数的后验密度曲线图 3.2 单因子MSV模型估计 数据选取后,接下来要对经过对数处理后的沪深300指数和ETF基金价格指数收益率进行单因子MSV模型参数估计,本文采用基于Gibbs抽样的MCMC方法做100000次循环迭代,舍去前80000个抽样值,使用后面的抽样结果作为各参数的稳定分布抽样,参数估计结果如表2所示。 由表2可知,各参数估计结果的蒙特卡洛误差都很小,且远小于标准差,而且从图1也可以看出Gelman-Rubin统计量随着迭代次数的增加而趋近于1,因此,可认为MCMC的估计结果是收敛的,参数估计值是有效的。由单因子MSV模型参数(μ,φ,σ,d,σε1,σε2)后验分布的核密度估计曲线(图2)可知,除d和σ外各个参数的核密度估计曲线的形状都比较平滑,各曲线也都随着参数的不同而发生变化,而且基本上都是单峰的,这也说明基于Gibbs抽样的MCMC方法很好地模拟了模型中各参数的边缘后验分布。波动持续性系数φ为0.9826,说明波动的冲击对股市与ETF基金市场的影响持续较长时间。图3的动态条件相关图表明,ETF与沪深300指数之间的相关系数在0.92与0.99之间波动,因此,股市与ETF基金市场之间是时变相关的,在不同经济周期、不同政策背景下会呈现出差异,但是都超过0.9,说明两市场的相关性较强,两市场的趋同性、一体化程度较高,这与ETF基金的独特的申购赎回交易机制有关。ETF的申购与赎回都是使用标的指数的成分股与份额互换,即使是ETF自身套利也是使用成分股进行,因而股票市场与ETF基金市场必然会产生很强的联动性。 采用公式:VaR=-μ+U1-ασ计算VaR值,其中U1-α为标准正态分布1-α水平分位数,本文中α=0.05,σ为标准差。然后将VaR值代入公式(4)-(8)计算CoVaR值和%CoVaR值,结果如表3所示。 由表3可知,ETF基金价格指数的VaR值为0.0126,小于沪深300股票指数的VaR值0.4544,说明股票市场的风险大于ETF基金市场。这是由于股票市场的股票种类和数量都大于ETF基金市场的股票种类和数量,当非ETF成分股的上市公司遭受风险时,EFT基金并未受影响而股票市场却或多或少会受到影响。因此,股票市场的风险来源更广,也更容易遭受风险。ETF基金市场向股票市场的风险溢出效应为82.3%,股票市场向ETF基金市场的风险溢出效应为225.7%,说明两市场间存在双向风险溢出效应,且股票市场向ETF基金市场的风险溢出效应更强。这可能是由于ETF基金的组成都是股票,因此,股票市场的风险必然会传染到ETF基金市场。而ETF基金选用的股票只是股票市场的一部分股票,因此,当ETF基金市场发生风险时,也会传染到股票市场,但是风险溢出的强度却不如股票市场向ETF基金市场溢出那么大。 表3 ETF基金价格指数与沪深300指数间风险溢出%CoVaR统计量 表3 ETF基金价格指数与沪深300指数间风险溢出%CoVaR统计量 风险溢出方向VaRiq,tCoVaRi|jq,t%ΔCoVaRi|jq,tETF®HS3000.01260.06582.3%HS300®ETF0.45440.3982225.7% 本文利用单因子MSV-CoVaR模型研究了我国股票市场与ETF基金市场之间的风险溢出效应,分析了股票市场与ETF基金市场间信息传递与风险传导方向,度量了两市场间的风险溢出强度,研究结果对进行两市场间的风险监管有一定的帮助,对投资者进行股票和ETF基金投资也有参考价值。基于上述研究,本文得出以下结论: (1)ETF基金市场与股票市场之间存在很强的相关性。ETF基金价格指数与沪深300指数之间的动态条件相关系数在0.92与0.99之间波动,表明股市与ETF基金市场之间是时变相关的。不同的经济周期和政策背景会对两市场的相关性产生不同的影响,但是两者的动态条件相关系数都超过了0.92,因此,两市场的相关性较强,两市场的趋同性、一体化程度较高。 (2)股票市场比ETF基金市场遭受更容易遭受风险。沪深300股票指数的VaR值为0.4544,大于ETF基金价格指数的VaR值0.0126,因此,股票市场的风险大于ETF基金市场,股票市场比ETF基金市场更容易遭受风险。ETF基金市场的成分股数量和种类只是股票市场的一小部分,因此,从风险来源来看, 股票市场也更容易遭受风险。 (3)股票市场与ETF基金市场之间存在不对称双向风险溢出效应,且股票市场对ETF基金市场的风险溢出效应要强于ETF基金市场向股票市场的风险溢出效应。股票市场向ETF基金市场的风险溢出效应为225.7%,ETF基金市场向股票市场的风险溢出效应为82.3%,因此,股票市场向ETF基金市场的风险溢出效应更强,这也是由于ETF基金成分股来源于与股票市场且数量和种类又少于股票市场的股票种类和数量所致。 [1] Hamao Y, Masulis R W, Ng V. Correlations in price changes and volatility across international stock markets[J]. Review of Financial Studies, 1990. 2(3): 281-307. [2] 洪永淼,成思危,刘艳辉,等. 中国股市与世界其他股市之间的大风险溢出效应[J]. 经济学(季刊), 2004. 3(3): 703-726. [3] 刘晓星,段斌,谢福座. 股票市场风险溢出效应研究:基于EVT-Copula-CoVaR模型的分析[J]. 世界经济, 2011,(11): 145-159. [4] 熊正德,韩丽君. 金融市场间波动溢出效应研究——GC-MSV模型及其应用[J]. 中国管理科学, 2013,21(2): 32-41. [5] 史永东,丁伟,袁绍锋. 市场互联、风险溢出与金融稳定——基于股票市场与债券市场溢出效应分析的视角[J]. 金融研究, 2013,(3): 170-180. [6] 柏满迎,吴琪,吴天都. 我国股票市场与基金市场间的风险溢出研究[J]. 统计研究, 2014,(4): 108-109. [7] Hong Yongmiao, Liu Yanhui, Wang Shouyang. Detecting extreme risk spillover between financial markets[R]. Working Paper,Cornell University, 2003. [8] Hong Yongmiao. Granger causility in risk and detection of risk between two time series[R]. Working Paper,Corneu University, 2001. [9] 潘慧峰,张金水. 国内外石油市场的极端风险溢出检验[J]. 中国管理科学, 2007,15(3): 25-30. [10] 李成, 马文涛,王彬. 我国金融市场间溢出效应研究——基于四元VAR-GARCH(1,1)-BEKK模型的分析[J]. 数量经济技术经济研究, 2010,(6): 3-19. [11] 熊正德, 文慧,熊一鹏. 我国外汇市场与股票市场间波动溢出效应实证研究——基于小波多分辨的多元BEKK-GARCH(1,1)模型分析[J]. 中国管理科学, 2015,23(4): 30-38. [12] 邓超, 陈学军. 基于复杂网络的金融传染风险模型研究[J]. 中国管理科学, 2014,22(11): 11-18. [13] 欧阳红兵,刘晓东. 中国金融机构的系统重要性及系统性风险传染机制分析——基于复杂网络的视角[J]. 中国管理科学, 2015,23(10): 30-37. [14] Adrian T, Brunnermeier M K. CoVaR[J]. American Economic Review,2016,106(7):1705-1741. [15] Girardi G, Ergün A T, Systemic risk measurement: Multivariate GARCH estimation of CoVaR[J]. Journal of Banking & Finance, 2013,37(8): 3169-3180. [16] 熊正德,韩丽君. 基于MSV类模型的中国汇市与股市间溢出效应[J]. 系统工程, 2010, 28(10): 47-53. [17] 张瑞锋,张世英. 基于VS-MSV模型的金融市场波动溢出分析及实证研究[J]. 系统工程, 2007, 25(8): 1-6. [18] Harvey A, Ruiz E, Shephard N. Multivariate stochastic variance models[J]. Review of Economic Studies, 1994,61(2): 247-264. [19] Jacquier É, Polson N G, Rossi P E. Models and priors for multivariate stochastic volatility[R]. CIRANO Working Paper,1995. [20] Jacquier É, Polson N G, Rossi P E. Stochastic volatility: Univariate and multivariate extensions[R]. CIRANO Working Paper, 1999. [21] Diebold F X, Nerlove M. The dynamics of exchange rate volatility: A multivariate latent factor ARCH model[J]. Journal of Applied Econometrics, 1989, 4(1): 1-21. [22] Yu Jun, Meyer R. Multivariate stochastic volatility models: Bayesian estimation and model comparison[J]. Econometric Reviews, 2006, 25(2-3): 361-384. Study on TheRisk Spillover Effect of China’s Financial Market Based on AFactor-MSV-CoVaR Model CHEN Jiu-sheng,ZHOU Xiao-hua (School of Economics and Business Administration,Chongqing University,Chongqing 400044,China) Under the background of economic globalization, with the process of the world economic integration, the free flow of information and capital becomes more clear, and the financial market risk transfer from one market to another market. Therefore, study of the risk spillover effect of financial markets has become the focus of financial supervision departments and scholars. In paper, the risk spillover effect between stock market and ETF market in china is analyzed based on CoVaR method combined with Afactor-MSV model. This combined model can measure the risk spillover effect between two different markets without copula functions, and it has higher fitting degree in reality than other models. In the first step, joint distribution model of stock market and ETF market is established by using the Afactor-MSV model, and MCMC method based on Gibbs sampling is put forward to estimate parameters of the combined model. Then, the risk spillover intensity between two markets is measured by using CoVaR function. Based on the daily prices of Chinese stock market index and ETF market index over January 4, 2010-April 30, 2015, our results demonstrate that there is two-way spillover effect between stock market and ETF market in china, the degree of risk spillover effect from stock market to ETF market is stronger than that of from ETF market to stock market. Meanwhile, it is also found that there is long-lasting effect of volatility shock on stock market and ETF Market. The empirical results can provide the reference for investors making investment decisions, and it is also valuable for regulation of financial markets. afactor-MSV; CoVaR; financial market; ETF market; risk spillover 1003-207(2017)01-0021-06 10.16381/j.cnki.issn1003-207x.2017.01.003 2015-05-29; 2015-12-29 国家自然科学基金面上项目(71373296);国家社科基金重大项目(14DB148) 陈九生(1985-),男(汉族),江西瑞金人,重庆大学经济与工商管理学院,博士研究生,研究方向:金融工程和风险管理等,E-mail:jiusheng_chen@163.com. F830 A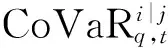
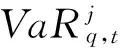
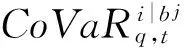


3 实证分析


4 结语
