救灾物资供应网络解构及结构优化模型
2017-04-19王熹徽
王熹徽,李 峰,梁 樑
(中国科学技术大学管理学院,安徽 合肥 230026)
救灾物资供应网络解构及结构优化模型
王熹徽,李 峰,梁 樑
(中国科学技术大学管理学院,安徽 合肥 230026)
本文依据采购-储存-运输三点决策过程,将现实中复杂的救灾物资供应网络解构为8类直线型物资供应链。构建了以最小化社会损失为首要目标的救灾物资供应网络的结构优化模型,该模型可在救灾行动绩效不降低的情况下,给出最优的最低成本物资供应链组合,或在成本不增加的情况下,得到最优的最大救灾行动绩效物资供应链组合。以5.30盈江地震为对象,利用真实数据对优化模型进行了验证,并在此基础上对不同情境下的优化结果进行了对比分析。研究发现,物资类型和地区类型变化会改变救灾物资供应网络的最优结构,但物资需求量的变化并不会显著改变救灾物资供应网络的最优结构,而只影响供应链的增减和物资承载量的增减。本研究厘清了救灾物资供应网络的构成和流程,为进一步优化奠定了基础,所提出的优化模型既可用于应急条件下救灾物资供应网络的即时构建,又可为和平时期救灾物资储备体系的建设提供方向性指导。
救灾物资供应网络;网络解构;结构优化;救灾应急运作管理
1 引言
近年来,世界范围内灾害频发,人类社会遭受了巨大的人员伤亡和财产损失。研究表明,全球每年约有500次灾害,共造成两亿人受灾,75000人死亡[1]。而在过去的十年中,仅自然灾害平均每年造成200亿美元的直接经济损失[2]。面对日益严峻的灾害形势,各救援组织都试图通过积极应对和科学决策以提高救灾应急管理水平,从而减少或避免人员伤亡,减轻或消除社会经济损失。在救援行动中,物资救援是满足生存需求和救援需求的关键,而救灾物流更是占据救援成本的80%以上[1]。虽然理论界和救援组织对救灾物资的供应问题进行了细致研究,也推出了一些具体措施,但是,在各个极端灾害的救援中,救灾物资延迟仍普遍存在。因救灾物资紧缺或延迟造成的损失,也约占灾害总损失的15%-20%[3]。我们认为,造成救灾物资供应低效的一个重要原因是救灾物资供应网络不合理,其结构优化水平低。一般而言,救灾物资供应网络涉及多个成员和多种决策与策略,所以,其现实结构非常复杂。而现有研究往往人为地选取一类供应链进行协调优化,这样即使存在最优解,也仅仅是局部最优。
本文主要研究救灾物资供应网络的组成结构和相应的结构优化问题。鉴于救灾物资供应网络的复杂性,现有研究中一部分主要着眼于客观存在的实体供应网络,并在固定的物理网络基础之上进行优化。如Sheu和Pan Cheng[4]为应对大规模自然灾害提出了集中式应急网络设计方法,Li等[5]研究了飓风灾害中的庇护所网络选址问题,文献[6-8]研究了应急物资配送中心的选址问题。其实质都是在备选地点集合中选出一个最优组合,使得灾害发生时救灾物资能够在最短时间内满足灾区的最大需求。此外,运输路径优化问题也是建立在客观存在的实体网络之上,如Campbell等[9-10]。另一部分研究则侧重于抽象的救灾物资供应网络(供应链)。一般认为,救灾物资运作管理问题应分为“获取-储存-分配/运输”三个阶段进行研究[11-12],从而构成了一条完整的救灾物资供应链[13-14]。以救灾物资供应链的视角来管理救灾物资,有助于提升救灾物资运作管理效率,从而更好地服务于灾害应急救援。但是,现有研究只是孤立地考察了其中一个或者两个点,人为地将救灾物资供应网络躯解。如Chakravarty[15]和Wang Xihui等[16]研究了救灾物资供应链中的采购问题,Ozguven和Ozbay[17]何Das和Hanaoka[18]进行了救灾物资库存问题研究,而Bozorgi-Amiri等[19]和Özdamar等[20]则考察了救灾物资供应链中的运输问题。国内学者对该问题的研究同样遵从实体网络与抽象网络两个维度。实体网络方面,杨继君和佘廉[21]和刘舒悦等[22]研究了救灾物资的优化调运问题,祁明亮等[23]和阮俊虎等[24]研究了救援物资的联合运送问题,张玲等[25]和倪冠群等[26]考察了应急避难点与配送中心的选址决策,刘长石等[27]则运用模糊方法研究了救灾物质的定位与路径规划问题。抽象网络方面,王熹徽和梁樑[28]和张琳等[29]从供应链的视角研究了救灾物资的采购问题,吴勇刚等[30]则研究了针对救灾物资的灾害应对策略,包括预先购买/即时购买与外包物流/自主物流。
从救灾物资供应网络的全过程来看,现有文献大都只研究了救灾物资供应链的一部分,或是在特定供应链结构下针对个别决策的局部优化问题,缺少对救灾物资供应链全局的把握。如Balcik和Ak[31]在研究供应商选择问题时自动采用了“灾前预先购买-供应商储存-供应商运输”的供应链结构;Chakravarty[32]则考察了一个“零售商-救助提供商-物流服务提供商-灾区”的救援链结构。对救灾物资供应链部分内容的优化,虽然可以在局部上提升救援绩效,但对整个救灾物资供应网络而言可能收效甚微。因为对一个救灾物资供应网络的局部进行诸如采购、储存、运输等优化决策,并不能得到一个适用于全局的最优解。虽然也有一些学者考察了救灾物资供应的全过程网络,如Altay等[33]提出了灾害救援的集成物流模型,Balcik等[11]提出了救灾物资供应的一般网络结构,但他们都仅仅提供了一个抽象的理论框架,并不能够进行建模分析。此外,Chakravarty[15]、吴勇刚等[30]和Wang Xihui等[34]的研究表明,不同的救灾物资供应链策略会导致不同的效能,而救援情境也影响着救援链的结构和运作。受此启发,我们认为,不同的救灾物资供应链具有不同的特征,应该被用于不同的灾害情境。这有两层含义,其一,不同的救灾物资供应链在不同的灾害情境中会产生不同的救援绩效;其二,不同的灾害情境应该采用不同的救灾物资供应链组合。鉴于此,本文将对救灾物资供应网络进行结构优化,决定不同灾害情境下最优的救灾物资供应链组合,以及每类独立供应链所承载的最优物资量。特别地,本文主要考察救灾物资的供应网络,并通过对其建模分析而给出灾害情境下的结构优化决策。该网络与已有研究的不同之处在于:(1)抽象网络;本文研究的救灾物资供应网络并不具有实体的物理结构,而是通过对救灾物资供应链运作过程的抽象而提炼出来的。(2)完整网络;本文的研究对象包含采购-储存-运输的完整结构,这样形成的网络具有一般性,可以转化为其他研究中的救灾物资供应结构;并且,这一网络将已有研究中单独考察采购、储存和运输的情况结合起来,形成一个整体框架。
借鉴商业物流的成功经验,从供应方到灾区,可以将救灾物资的获取-储存-分配/运输看作一条完整的救灾物资供应链[12-14]。但是,由于每个决策点的策略不唯一,救灾物资供应链的类型也具有多样性。鉴于此,如何分解救灾物资供应网络,如何梳理救灾物资供应链,如何对不同的救灾物资供应链进行安排,进而如何优化不同情境下的救灾物资供应网络就成为了一个值得探讨与研究的科学问题。本文将在已有研究的基础上,利用三个供应链决策点,从复杂的救灾物资供应网络中解构出8类救灾物资供应链,每一类都对应一个可行的救灾物资供应通路。在给定灾害情境和供应链的情况下,可以对救灾物资供应链的结构选择和物资分配进行决策。本文构建了救灾物资供应网络的结构优化模型,该模型以最大化社会性救援绩效为首要目标,并追求经济成本的最小化。最后,我们对模型进行了基于真实例子的数值分析和应用,并在此基础上进行了一些扩展讨论。与已有研究相比,本文具有一些显著的特征:1)将复杂的救灾物资供应网络进行了合理分解,该分解方法所得的物资供应链集合具有完备性,独立性和决策过程完整性的特征,且有助于厘清物资供应网络的构成和流程,为进一步的优化奠定了基础。2)优化模型同时考虑了救灾行动绩效的社会性和经济性,比大多数已有的优化模型更加符合救灾运作管理的现实考量,更加符合现实。3)优化模型经过了真实案例和数据的检验,并可在此基础上进行演绎和拓展分析,具有较强的解释力。
2 救灾物资供应网络解构
2.1 救灾物资供应网络
灾害救援涉及到国际救援组织、地方政府、军队、地方和区域救援组织、私人企业、捐赠者以及受灾群众等多个成员[11]。根据他们承担的责任,可以划分为救援组织、供应商、物流企业和灾区。救援组织是救援的领导者和驱动者,负责实施灾害救援,同时也是救灾物资的买方。救援组织主要包含三类,国际组织、政府部门和非政府组织[35],任何领导或驱动救灾物资供应链的主体都可以归于救援组织。救援组织可以独立完成救援行动,也可以将部分内容外包给其他主体。供应商是救灾物资的来源,包括营利性的商业机构和慈善性的捐赠(本文不考虑商业购买与慈善捐赠的差别,把他们都抽象为购买)。供应商除提供救灾物资外,还作为附加服务地提供储存服务和运输服务。物流企业具有专业化的大批量快速物流经验,作为第三方物流策略为救援组织提供救灾物资的运输服务,这一点在长距离大批量的救灾物资运输中显得尤为重要。灾区是所有受灾群众的集合,也是救灾物资的目的地。由此,根据Balcik等[11]的研究,可以将救灾物资供应网络抽象成图1所示的网络结构。图中6个节点分别是供应商、救援组织、物流企业、供应商仓库、救援组织仓库以及灾区。图中共有13条代表救灾物资单向流动的方向箭线,如L2表示救灾物资从供应商流向供应商仓库,L10表示救灾物资从救援组织仓库流向灾区。每一条从供应商到灾区的通路都是可实现救灾物资供应的独立的救灾物资供应链,如路径L2L6表示灾前预先购买救灾物资,并由供应商负责救灾物资的储存以及灾后运输,这正是Balcik和Ak[31]研究供应商选择问题时采用的救灾物资供应链。
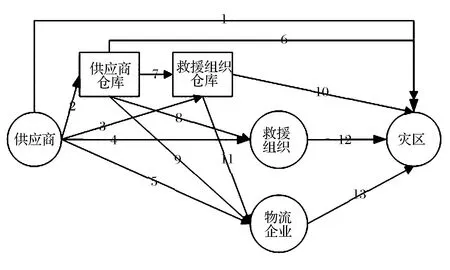
图1 救灾物资供应链的网络结构
2.2 救灾物资供应链的决策过程
从图1中的网络结构可以看出,救灾物资单向性地从供应商流向灾区。救灾物资在供应网络中的流动方向受到决策过程的影响,不同的决策对应不同的流动方向,并涉及不同的网络成员,从而组合成为不同的救灾物资供应链。由此可见,厘清救灾物资供应的决策过程,是分解一个复杂的救灾物资供应网络的关键。根据Balcik等[11]和王熹徽[14]的研究,救灾物资供应的决策流程如图2所示,依次有采购、储存和运输三个决策点。每一决策都有几种不同的策略,而不同的策略具有不同的特征,并有可能产生完全不同的救援结果。
(1)采购。救灾物资的采购策略可以分为灾前预先采购和灾后即时采购两种方式。虽然灾后即时购买是救灾物流中最常见的采购方式[31,36],但灾前预先购买是应对可预测或季节性灾害的有效手段。并且,即时购买通常成本较高,交货提前期时间长,而预先购买的救灾物资则单价低,但风险损失大,且增加了库存成本[14,16]。
(2)储存。救灾物资的储存策略可以分为供应商储存、救援组织储存与灾后即时购买救灾物资时的零库存三种方式。储存决策与采购决策密切相关,一般而言,只有预先购买的物资才需要专门考虑储存决策。由于本文假定所有物资来源都是供应商,因此,供应商的储存能力可以看作无限大,而救援组织的储存能力则常常受到限制[11]。并且,供应商储存策略由于使用了供应商的商业经验,可以有效降低储存成本,但也使得救援组织的监管成本增加;而救援组织储存虽然几乎没有监管成本,但储存成本通常较高[30,34]。供应商储存与救援组织储存的经典例子是沃尔玛与FEMA,二者在2005年卡特丽娜飓风前后的救灾物资储备中结果大相径庭[37-38]。
(3)运输。救灾物资的运输策略可以分为救援组织运输、供应商运输和物流企业运输三种方式,即是由救援组织、供应商还是物流企业将救灾物资从仓库或即时购买的供应商处运输到灾区。一般而言,救援组织不具有城市地区快速物流的经验[30],但其在偏远地区或道路通行条件差的灾区具有较大优势。供应商的运输仅是一种附加服务,在城市地区和交通条件好的灾区具有最大的价格优势,且运能巨大。物流企业运输是第三方物流策略,具有丰富且成功的商业物流经验,在救援组织运能不足时可以进行有效替代与补充。
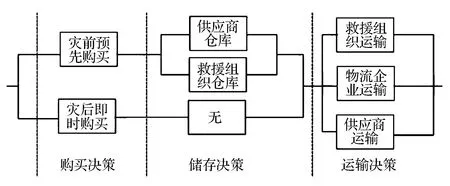
图2 救灾物资供应链的决策过程
2.3 救灾物资供应网络解构
图2中的救灾物资供应链决策过程是与图1中的救灾物资供应网络相对应的。如此,根据图2的决策过程可以将图1的救灾物资供应网络解构为表1中的8类救灾物资供应链,并且,每一类供应链都可以实现救灾物资从供应商向灾区的转移。这一分解具有完备性、独立性和决策过程完整性的特征:(1)完备性:所有供应链一起构成了图1中的完整网络;(2)独立性:每两类供应链之间彼此独立且互不影响;(3)决策完整性:每一类供应链都经历了采购-储存-运输三决策。解构救灾物资供应网络得到的供应链结构如表1所示。

表1 救灾物资供应链
这8类救灾物资供应链的组合,可以构成任意救灾物资供应网络。即任意救灾物资供应网络都可以由所分解得出的8类救灾物资供应链组合所得。由于各供应链具有不同的特征,因此如何恰当的组合这些供应链,形成一个可以适用于特定灾害的救灾物资供应网络,以实现救援绩效最大化目标,是本文的另一个重要研究内容。
3 救灾物资供应网络结构优化模型
3.1 符号说明
为表述方便,本文所使用的数学符号解释如下:
决策变量:
qit:供应链i∈N在时间t内所承载的物资量;
参数:
X:救灾物资需求量;
r:物资短缺产生的单位社会损失;
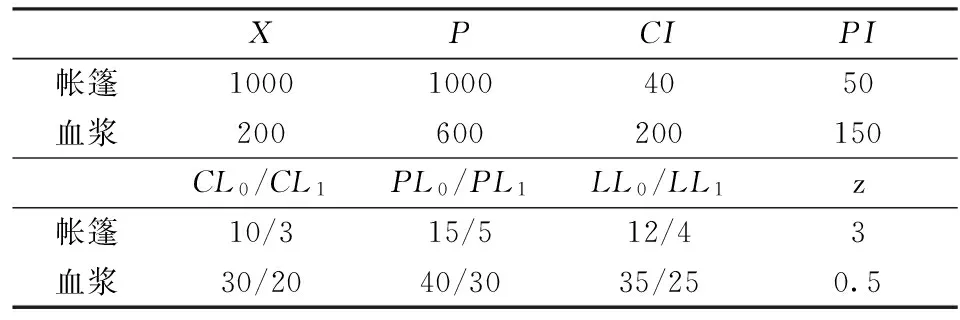
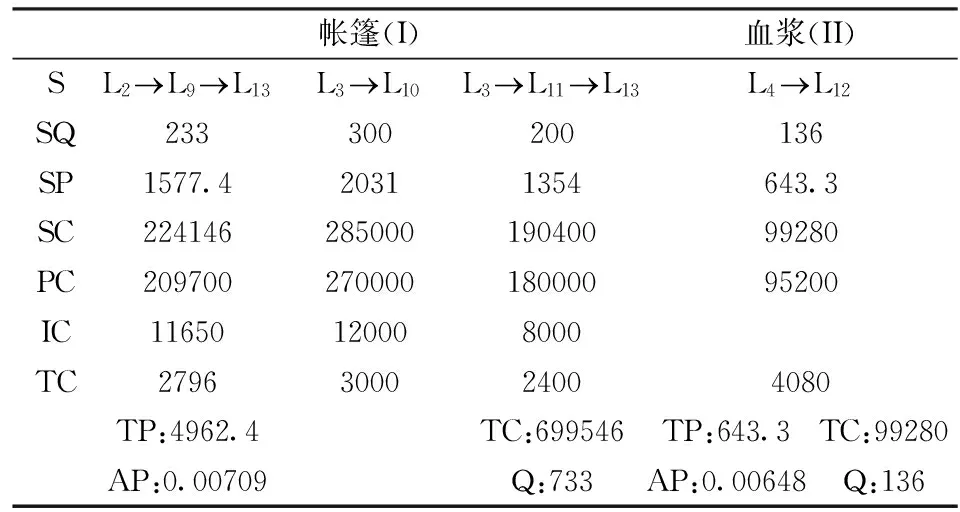
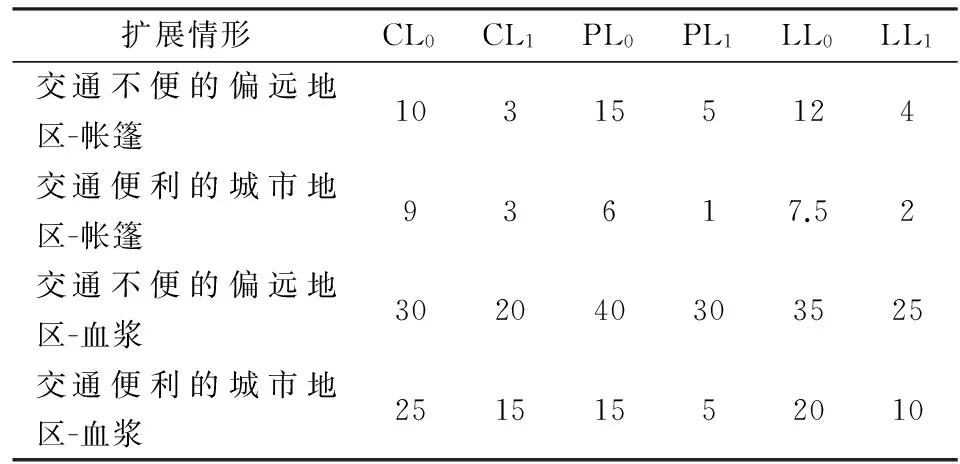
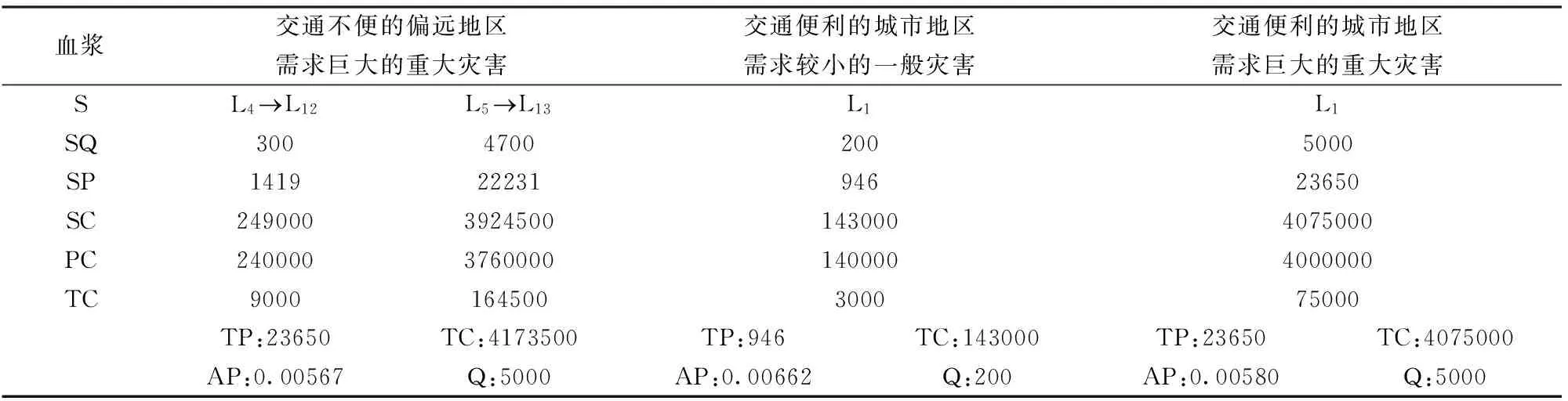
a:服务要求,即在t B:资金约束; τi:供应链i∈N下的物资保存时间,与灾害有关; z:物资的保质期; Imax:救援组织的最大储存能力; Lmax:救援组织的最大运输能力; μit:供应链i∈N在时间t内所承载物资产生的单位社会损失; pi:供应链i∈N所承载物资的单位购买价格; PIi:供应链i∈{4,5,6}所承载物资的(供应商)单位储存价格; PLi:供应链i∈{1,4}在时间t内所承载物资的(供应商)单位运输价格; CIi:供应链i∈{7,8}在时间t内所承载物资的(救援组织)单位储存成本; CLi:供应链i∈{2,5,7}在时间t内所承载物资的(救援组织)单位运输成本; LLi:供应链i∈{3,6,8}在时间t内所承载物资的 (物流企业)单位运输价格; t1:快速物流时间临界点,一般取值为黄金救援时间72小时; t2:救援行动的时间临界点,一般认为,当t>t2时救援效果为0; N:供应链集合,且有i∈N={1,2,…,8}。 3.2 模型构建 3.2.1 目标函数 根据Holguín-Veras等[39]的观点,救灾物流优化模型应该使用社会性的成本作为其目标函数。据此,本文利用社会损失的概念来测度救援行为的绩效。在所有灾害救援情境中,最坏的救援结果是,没有任何救援物资抵达灾区,并且所有需求都得不到满足,此时社会损失达到最大,表示为r·X。而任何其他有救灾物资运抵的救援行动,其造成的社会损失都不会大于上述情境下的社会损失,并且运抵数量越多、运抵时间越短,社会损失越小。鉴于此,我们使用某一救援行动最终导致的社会损失与最大社会损失之间的差额来表示该物资救援行动的绩效。 P=rX-[r·max(X-Q,0)+∑i∈N∑t∈Tμitqit] (1) 其中,Q=∑i∈N∑t∈Tqit是灾害救援中的物资总量。在本文中,社会损失包含两部分,时间延迟产生的社会损失和物资短缺产生的社会损失[32],物资短缺量由max(X-Q, 0)给出。 经济成本也是衡量救灾行动绩效的重要指标之一,必须在模型中加以考虑。但本文与Holguín-Veras等[39]给出的方法不同,在其研究中救援的总成本由经济成本加上社会成本构成。这种做法意味着经济成本与社会成本之间具有可替代性,即可以以社会成本为代价换取经济成本的减少。我们认为,救援行动的主要目的是尽可能地在数量和时间上满足对于救灾物资的需求,从而最大限度地减轻灾民痛苦。因此,物资救援的社会成本应该是优先于经济成本的,这样的做法才更符合“人道物流”(HumanitarianLogistics)的非牟利性。经济成本由(2)式表示, C=∑i∈N∑t∈T[(pi+PIi·τi/z+CIi·τi/z+PLit+LLit+CLit)·qit] (2) 上式中,第一项是救灾物资的采购成本;第二、三项是储存成本,当采取灾后即时采购的策略时,储存成本为零;第四、五、六项表示运输成本。 基于上述分析,模型的目标函数应包含如下两个因素:救援行动的绩效和经济成本,且绩效的优先级高于经济成本。由此本文采用Max(P-ε·C)作为模型的目标函数。该目标函数包含两部分:第一部分是社会性的救援绩效P,第二部分是经济成本与非阿基米德无穷小项的乘积ε·C。对于该目标函数的求解可分为两个步骤:(1)极大化测度救援绩效的多项式;(2)在保持第一步中最大绩效不减小的前提下,极小化经济成本。 3.2.2 模型 构建救灾物资供应网络结构优化模型: Max(P-ε·C) (3a) s.t.C≤B (3b) ∑t∈T(q7t+q8t)≤Imax (3c) ∑t∈T(q2t+q5t+q7t)≤Lmax (3d) ∑i∈N∑t (3e) (3f) 模型中,式(3a)为目标函数;式(3b)是物资救援的预算约束;式(3c)和(3d)给定救援组织的储存能力约束和运输能力约束;式(3e)是基于快速物流的物资救援服务要求,它要求救灾物资需求的一部分能够在时间t 3.3 分析 上节给出了求解救灾物资供应网络结构优化问题的一般模型。为更好的解释该模型,本节主要对模型中的参数关系进行讨论,并对模型中的部分参数进行了简化约定和分析。 (1)采购。预先购买与即时购买具有不同的定价。一般而言,预先购买的单位价格低于即时购买[15]。并且,在使用价格柔性供应链契约时,大批量订购可以给预先购买带来价格折扣[31]。但是,灾害发生时物资需求急剧增加,这会抵消价格折扣,并随着采购量的增加,单位价格也增加。因此,本文假定灾前预先购买仅有数量折扣效应,而灾后即时购买只存在价格膨胀效应。本文假定采购定价是二阶段的阶梯函数,用pr表示即时购买的物资单位价格,用pp表示预先购买的物资单位价格: 其中,p1>p0>p2>p3。影响购买定价的一个主要外部因素是需求量,而需求量又与灾害密切相关。按照灾害的破坏程度和所造成的影响,可以将灾害分为重大灾害和一般性灾害[31]。一般而言,重大灾害发生概率低,但破坏性大,产生的救灾物资需求量也大;而一般性灾害发生概率高,但破坏性通常较小,产生的救灾物资需求量也小。与采购定价联系起来,本文假设存在两种需求情况,即需求量远远大于数量阈值Q0的重大灾害,以及需求量稍大于甚至小于数量阈值Q0的一般性灾害。 (2)储存。救援组织的储存费用包括直接的储存成本与间接的监管成本,而储存成本受到物资类型的影响。遵循Dignan[40]的做法,救灾物资可以分为易腐物资和非易腐物资两类。易腐物资如食物、水和药品,要求严格的存放和储存条件,保质期短且价格昂贵;而非易腐物资如帐篷、棉被,处置较为简单,保质期也较长,只要保持使用前的不毁坏即可。本文假定,供应商的储存成本较救援组织低,且其成本优势在存储易腐物资时更为明显[30,34]。考虑到救援组织的监管费用,则对于易腐物资,即使加上监管费用,供应商仍具有储存的价格优势,即有PI (3)运输。运输价格跟时间要求有关,且运输价格是时间的非增函数。即要求把救灾物资运送到灾区的时间越短,运输价格越高,反之则越低。此处也假定运输价格是两阶段的阶梯函数:当t (4)社会损失函数。Holguín-Veras等[39]专门探讨了救灾物流的社会损失函数,本文采用王熹徽和梁樑[28]的假设,即假定所有供应链的提前期相同,并因此同一物资在不同供应链中的损失函数相同。本文采用分段阶梯函数来刻画社会损失函数:当t 4.1 案例背景 2014年5月24日,云南省盈江县发生里氏5.4级地震。六天之后,又发生里氏6.1级地震。截止6月1日,共发生余震1333次,并包括2次4.0—4.9级余震和1次5.0—5.9级余震。这次地震共造成45人受伤,29996户民房受损,51202户居民受灾(http://www.dehong.gov.cn/news/dh/content-16-15551-1.html)。我们在震后15天到达盈江,并于6月11日走访重灾区,对当地居民进行问卷调查以获取社会性变量数据,并通过实地考察获取了经济性变量。以非易腐物资-帐篷和易腐物资-血浆为例,采用NRS 0-10测度法,得到其社会损失均值如表2。对提供帐篷的供应商和治疗受伤灾民的医院进行了调查,得到主要的经济性变量如表3所示。 表2 社会损失均值 表3 经济性变量参数 以第三节模型为基础,对上述数据进行简化约定,得到盈江地震的救灾物资供应网络结构优化问题的两个基本案例,数据如表4。其中,单位社会损失取3日均值和7日均值,因为灾后72小时对于救援至关重要[41],因此可把社会损失的3日均值作为快速物流的社会损失;同样地,可把社会损失的7日均值作为标准物流的社会损失。 4.2 结果 对4.1中帐篷和血浆的例子进行救灾物资供应网络结构优化求解,计算采用Matlab_2012a,得到结果如表5(假设预算约束无穷大)。由于预算约束无穷大,即预算资金可以满足所有物资需求,所以,表5的结果表明,无论是易腐物资-血浆,还是非易腐物资-帐篷,在实现极大化救援绩效P时,都满足了救灾物资的全部需求。 表4 案例数据 表5 求解结果(无预算约束) 注:S表示供应链结构,SQ表示各供应链承载的物质数量,SP表示绩效,SC表示成本,PC、IC与TC分别表示购买成本、储存成本与运输成本。TP、TC、AP、Q分别表示灾害情景下的总绩效、总成本、平均绩效和物质总量。下文类似。 对于帐篷,可以通过1000单位物资实现最大的绩效6770,其最小成本是956400,平均绩效0.00708。帐篷的最优供应网络由四种供应链构成:1)L2L8L12是预先购买并将物资储存于供应商仓库,灾后由救援组织运送物资;2)L2L9L13是预先购买并将物资储存于供应商仓库,但灾后由物流企业运送物资;3)L3L10是预先购买物资,并由救援组织负责物资的储存与运输;4)L3L11L13是预先购买并将物资储存于救援组织的仓库中,灾后由物流企业运送物资。可以发现,所有供应链都预先购买物资,这是因为,对非易腐物资而言,预先购买的价格折扣可以抵补预先购买的储存费用,预先购买是有利可图的。与图1的救灾物资供应链决策过程相联系,即有,全部1000单位物资均预先购买,并将500单位储存于供应商仓库,500单位储存于救援组织的仓库中;灾后由救援组织运送300单位,物流企业运送700单位。事实上,表5中的结果并不唯一,只要满足前述决策关系,即能够以最小成本956400实现最大绩效6770。对于血浆,可以通过满足200单位的需求实现最大绩效946,其最小成本是146000,平均绩效是0.00648。血浆的最优供应网络仅有一种供应链L4L12,即灾后即时购买,并由救援组织负责将物资运送到灾区。 通过分析可以发现: 1)易腐物资的储存费用非常高,不宜预先购买并储存。非易腐物资预先购买的价格折扣可以完全抵补其储存费用,故适于预先购买并储存;并且,救援组织是非易腐物资储存的第一选择。 2)盈江地处偏远地区,交通不便,此时,救援组织具有最大运输价格优势,故无论是易腐物资,还是非易腐物资,都首先通过救援组织运送,其次才通过第三方物流企业运送。供应商的运输服务在交通不便的偏远地区不适用。 3)即便是同一灾害的救援行动中,易腐物资和非易腐物资具有完全不同的最优物资供应网络,即不同的物资类型应当使用不同的物资供应网络。易腐物资的网络结构更简单。 4)救灾物资的最优供应网络是8种供应链的组合,但不会使用全部类型的供应链。表5及后文的数值结果表明,至多四种供应链就能够构建最优的救灾物资供应网络。 表6 求解结果(预算约束) 进一步地,我们考虑受到预算约束影响的情况。简单地,我们取表5中最小成本的一部分作为预算约束,并进行救灾物资供应网络结构优化求解。取帐篷的预算约束为700000,血浆的预算约束为100000,得到新的结果如表6。此时,帐篷的最优网络由三种供应链构成,供应链L2L8L12不再使用。事实上,当预算减少到475400(285000+190400)时,最优网络仅由L3L10和L3L11L13构成;当进一步减少到315000时,最优网络仅有L3L10。而对于血浆,由于表5中其最优网络仅有一种供应链L4L12,预算减少并不会改变最优网络,而只会改变物资量。 在现实中,救援组织是灾害救援的第一主体,但其能力通常有限,表现为运能有限、储备能力有限等。此时,需要使用供应商和物流企业的能力作为补充,实现救援组织与私人企业的联合,以最终实现使用最小成本达到最大绩效的目的。 4.3 讨论 4.2节就盈江地震中的易腐物资(血浆)和非易腐物资(帐篷)为例,给出了本文的救灾物资供应网络结构优化模型求解。但是,正如3.3节所阐述的那样,救灾物资供应链的决策过程(购买,储存,运输)受到诸多外部因素如,救灾物资的需求数量、救灾物资类型和受灾地区交通运输条件等的影响。通过对4.2节的回顾可以发现,盈江地震可以刻画为一个发生在偏远地区的一般性灾害,因此所给出的结论仅适用于需求量较小(一般性灾害),运输条件不便(偏远地区)情境下的救灾物资供应问题。 本节以4.2节所给出的结构优化结果为基础,对如下三种情况的救灾物资供应网络结构优化问题进行了扩展讨论:1)发生需求量巨大的重大灾害情况下;2)灾害发生在运输条件便利的城市地区情况下;3)需求量巨大,且运输条件便利情况下。我们假设,当发生重大灾害时,所有物资的需求都显著增大,此时,帐篷的需求是10000单位,血浆的需求是5000单位。当灾害发生在交通便利的城市地区时,各类物资的运输成本会发生显著变化。此时,帐篷和血浆的运输价格如表7所示。本节所有内容都假定预算约束无穷大。 表7 盈江地震救灾的扩展情形 首先,我们对帐篷的供应网络结构优化问题进行讨论,结果如表8所示。主要结论有: 1)重大灾害导致需求扩大,但并不会显著改变救灾物资的最优供应网络。表8中,需求量巨大情境下的最优结构与表5基本类似,而交通便利地区需求量巨大情境与需求量较小情境下的结果也类似。这表明,在特定地区,对于特定物资类型,有较稳定的救灾物资供应网络的最优结构。这意味着,救援组织可以分区域地规划设计各地的救灾物资供应网络,这种网络对于灾害本身具有一定的稳定性,不会因救灾物资需求总量的变化而显著改变。 2)灾害发生地区的交通运输情况会显著改变救灾物资供应网络的最优结构。无论是需求量巨大的重大灾害,还是需求量较小的一般性灾害,当灾害从交通不便的偏远地区移向交通便利的城市地区时,易腐物资(帐篷)的最优结构都完全改变。这表明,设计救灾物资的最优供应网络时,必须结合各自的区域特征,地区间构建最优救灾物资供应网络的经验并不能简单地复制,需要因地制宜。 对于易腐物资-血浆,其扩展讨论的计算结果如表9所示。上述对于非易腐物资的结论对于易腐物资同样适用,即救灾物资需求总量的变动会影响各供应链承载的物资量,但不会显著改变救灾物资供应网络,而地区类型的变化会显著改变救灾物资的供应网络。 通过分析可以发现,当救灾的外部环境发生变化时,救灾物资供应网络的最优结构会有不同的变化。1)物资类型改变,会显著影响救灾物资供应网络的结构;2)地区类型变化,救灾物资供应网络的最优结构也会显著改变;但是,3)需求数量的变化,并不会显著改变救灾物资供应网络的最优结构,其影响主要表现为供应链的增减和物资承载量的增减。总之,不同的灾害情境有不同的最优救灾物资供应网络,其由不同的供应链组合而成。 表8 帐篷的扩展情形 表9 血浆的扩展情形 本文主要研究了救灾物资供应网络的组成结构和相应的结构优化问题。通过对复杂的救灾物资供应网络的抽象分析,本文依据救灾物资供应链的三点决策过程,将现实中复杂的救灾物资供应网络解构为8类直线型物资供应链,这一分解具有完备性、独立性和决策过程完整性的特征。这一过程有助于厘清救灾物资供应网络的构成和流程,为进一步的优化奠定了基础。本文构建了救灾物资供应网络的结构优化模型,该模型以最小化社会损失为首要目标,并追求经济成本的最小化。该模型既可用于应急条件下救灾物资供应网络的即时构建,又可为和平时期救灾物资储备体系建设的提供方向性指导。本文以5.30盈江地震为对象,利用真实数据对优化模型进行了验证,结果显示该模型可以用于应急条件下真实灾害救援行动的分析和优化。在此基础上,本文通过调整参数、改变外界环境条件,对不同情境下模型的优化结果进行了对比和分析,得到了一些有助于未来救灾物资储备体系建设的指导性方针。 研究发现,任何一个救灾物资供应网络都可以通过采购、储存和运输这一决策过程分解为所列8类直线型物资供应链集合的一个子集,任何灾害情境的救灾物资供应网络都可以由这8类供应链组合而成。并且,本文所给出的救灾物资供应网络优化模型,可以在确保救灾行动绩效不降低的情况下,寻找出最优的最低成本物资供应链组合,或在确保成本不增加的情况下,寻找出最优的救灾行动绩效最大的物资供应链组合。在盈江地震中,易腐物资(血浆为例)不应预先购买并储存,而非易腐物资(帐篷为例)则可预先购买并储存,且首选由救援组织储存;救灾物资的运输则由救援组织和物流企业完成。此外,我们发现即便是同一灾害的救援行动中,易腐物资和非易腐物资具有完全不同的最优供应网络,易腐物资的供应网络结构更简单。当救灾行动的外部环境发生变化时,救灾物资供应网络的最优结构会有不同的变化。研究表明,物资类型和地区类型变化会改变救灾物资供应网络的最优结构,而物资需求量的变化,并不会显著改变救灾物资供应网络的最优结构,其影响主要表现为供应链的增减和物资承载量的增减。 注意到,本文关于救灾物资供应网络的部分结论并非新物,且得到了学术界的普遍认可,但以往研究多是从理论框架上进行陈述,而本文通过数学模型对这些结论进行了验证。并且,基于盈江地震真实数据的应用,表明本文能够得到正确的结论,能够为救灾应急运作管理实践提供客观指导和借鉴。但是,由于救灾应急运作管理在全球范围内都是一个新兴问题,这些一般规律在现实中却屡次遭到违背,比如,美国联邦紧急事务管理署(FEMA)多次违背“易腐物资不易储存而非易腐物资适于储存”这一结论。一方面,鉴于2005年沃尔玛在卡特莉娜飓风中利用自己的物资储备进行自发救援的成功经验和发挥的显著作用,FEMA在2006年采取了类似的措施,即在灾害发生之前就预先进行大量实物储备,包括易腐性物资和非易腐性物资。但是,预期的飓风却没有在2006年发生,而所储备的易腐性物资由于保质期等原因不得不销毁,结果造成大量的浪费[37-38]。另一方面,FEMA又于2009年将食物、水等易腐物资纳入到了其实物储备体系的采购清单之中[42],这显然违背了学界和业界的共识。面对诸如此类的救灾应急运作管理实践,本文的结论再次强调了在实践中遵守相应一般规律的重要性。只有严格遵守这些规律,才能在社会性救援绩效和经济性救援成本的双目标下提升救灾应急运作管理水平,并更好地实施灾害救援运作。 需要指出的是,本文研究的一个基本假设是:同一物资在不同供应链中的损失函数相同。这意味着,不同供应链的差别仅体现在组成成员和价格(成本)参数上,这显然是对现实情况的一种简化。事实上,不同供应链在协调难度、提前期等方面都有不同。因此,未来研究可以针对损失函数的差异性,构建适用于不同情境下的救灾物资供应网络的优化模型。此外,本文依据供应链决策过程中的采购、储存与运输对救灾物资供应网络进行了分解,并在此基础上给出了优化模型。但是,这并不是唯一的分解方式,其他决策点的运用应当也能够分解和优化救灾物资供应网络。因此,未来研究可以考虑对供应链决策过程进行系统性考量,从其他角度对救灾物资供应网络进行分解和优化。 [1] Van Wassenhove L N. Humanitarian aid logistics: Supply chain management in high gear [J]. Journal of the Operational Research Society, 2006, 57(5): 475-489. [2] Benfield A O N. Annual global climateand catastrophe report, impact forecasting-2013[R].Annual Report,Prevention Web,2014. [3] 冯海江.地震灾害救援中的应急物资分配优化研究[D].上海:上海交通大学,2010. [4] Sheu J B, Pan Cheng. A method for designing centralized emergency supply network to respond to large-scale natural disasters [J]. Transportation Research Part B: Methodological, 2014, 67: 284-305. [5] Li A C Y, Nozick L, Xu Ningxiong, et al. Shelter location and transportation planning under hurricane conditions [J].Transportation Research Part E: Logistics and Transportation Review, 2012, 48(4): 715-729. [6] Balcik B, Beamon B M. Facility location in humanitarian relief [J]. International Journal of Logistics-Research and Application, 2008, 11(2): 101-122. [7] Lu C, Sheu J B. Robust vertex p-center model for locating urgent relief distribution centers [J].Computers & Operations Research, 2013, 40(8): 2128-2137. [8] Naji-Azimi Z, Renaud J, Ruiz A, et al. A covering tour approach to the location of satellite distribution centers to supply humanitarian aid [J]. European Journal of Operational Research, 2012, 222(3): 596-605. [9] Campbell A M, Vandenbussche D, Hermann W. Routing for relief efforts [J]. Transportation Science, 2008, 42(2): 127-145. [10] Özdamar L, Demir O. A hierarchical clustering and routing procedure for large scale disaster relief logistics planning [J]. Transportation Research Part E: Logistics and Transportation Review, 2012, 48(3): 591-602. [11] Balcik B, Beamon B M, Krejci C C, et al. Coordination in humanitarian relief chains: Practices, challenges and opportunities [J]. International Journal of Production Economics, 2010, 126(1): 22-34. [12] Thomas Y. Supply chain reliability for contingency operations[C]//Proceedings of the conference on Annual Reliability and Maintainability Symposium, January 28-31,2002. Seattle, USA. [13] Whybark D C. Issues in managing disaster relief inventories [J]. International Journal of Production Economics, 2007, 108(1-2): 228-235. [14] 王熹徽.救灾供应链协调策略与契约定价研究[D].合肥:中国科学技术大学,2012. [15] Chakravarty A K. A contingent plan for disaster response [J]. International Journal of Production Economics, 2011, 134(1): 3-15. [16] Wang Xihui, Li Feng, Liang Liang, et al. Pre-purchasing with option contract and coordination in a relief supply chain [J]. International Journal of Production Economics, 2015, 167: 170-176. [17] Ozguven E E, Ozbay K. A secure and efficient inventory management system for disasters [J]. Transportation Research Part C: Emerging Technologies, 2013, 29(4): 171-196. [18] Das R, Hanaoka S. Relief inventory modelling with stochastic lead-time and demand [J]. European Journal of Operational Research, 2014, 235(3): 616-623. [19] Bozorgi-Amiri A, Jabalameli M S, Al-e-Hashem S M J M. A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty [J].OR Spectrum, 2013, 35(4): 905-933. [20] Özdamar L, Ekinci E, Küçükyazici B. Emergency logistics planning in natural disasters [J]. Annals of operations research, 2004, 129(1-4): 217-245. [21] 杨继君,佘廉.面向多灾点需求的应急资源调度博弈模型及优化[J].中国管理科学, 2016,24(8): 154-163 [22] 刘舒悦,朱建明,黄钧,等.地震救援中基于信息实时更新的两阶段应急物资调配模型[J].中国管理科学,2014,24(9):124-132. [23] 祁明亮,秦凯杰,赵琰.雪灾救援物质车辆-直升机联合运送的调度问题研究[J].中国管理科学,2014,22(3):59-67. [24] 阮俊虎,王旭坪,杨挺.大规模灾害中基于聚类的医疗物资联合运送优化[J].中国管理科学,2014, 22(10): 80-89. [25] 张玲,陈涛,黄钧.基于最小最大后悔值的应急救灾网络构建鲁棒优化模型与算法[J].中国管理科学,2014,22(7):131-139. [26] 倪冠群,徐寅峰,徐玖平.考虑道路通行能力的应急避难点选址模型及算法[J].中国管理科学, 2015, 23(1): 82-88. [27] 刘长石,彭怡,寇纲.震后应急物资配送的模糊定位-路径问题研究[J].中国管理科学,2016, 24(5): 111-118. [28] 王熹徽,梁樑.救灾供应链采购策略及契约协调机制研究[J].中国管理科学,2013, 21(4): 62-73. [29] 张琳,田军,杨瑞娜,等.数量柔性契约中的应急物资采购定价策略研究[J].系统工程理论与实践,2016,36(10):2590-2600. [30] 吴勇刚,王熹徽,梁樑.基于社会损失的灾害应对策略评估框架[J].系统工程理论与实践. 2015, 35(5): 1144-1154. [31] Balcik B, Ak D. Supplier selection for framework agreements in humanitarian relief [J]. Production and Operations Management, 2014, 23(6): 1028-1041. [32] Chakravarty A K. Humanitarian relief chain: Rapid response under uncertainty [J]. International Journal of Production Economics, 2014, 151(5): 146-157. [33] Altay N, Prasad S, Sounderpandian J. Strategic planning for disaster relief logistics: Lessons from supply chain management [J]. International Journal of Services Sciences, 2009, 2(2): 142-161. [34] Wang Xihui, Wu Yunfei, Liang Liang, et al. Service outsourcing and disaster response methods in a relief supply chain [J]. Annals of Operations Research, 2016,240(2): 1-17. [35] Beamon B M, Balcik B. Performance measurement in humanitarian relief chains [J]. International Journal of Public Sector Management, 2008, 21(1): 4-25. [36] Bhattacharya S, Hasija S, Van Wassenhove L K. Designing efficient infrastructural investment and asset transfer mechanisms in humanitarian supply chain [J]. Production and Operations Management, 2014, 23(9): 1511-1521. [37] Barbaro M, Gillis J. Wal-Mart at forefront of hurricane relief [N]. The Washington Post, September 6,2005. [38] Rosegrant S. Wal-Mart’s response to Hurricane Katrina: Striving for a public-private partnership[R]. The Kennedy School of Government Case Program C16-07-1876.0. Cambridge, MA: Kennedy School of Government Case Studies in Public Policy & Management, 2007. [39] Holguín-Veras J, Pérez N, Jaller M, et al. On the appropriate objective function for post-disaster humanitarian logistics models [J]. Journal of Operations Management, 2013, 31(5): 262-280. [40] Dignan L. Tricky currents; Tsunami relief is a challenge when supply chains are blocked by cows and roads doesn’t exist [J]. Baseline, 2005, 29(1): 30. [41] Hodge N. Rescue ops in Haiti: ‘The first 72 hours are critical’[J/OL]. WIRED. [2010-01-14].https://www.wired.com/2010/01/rescue-ops-in-hasi-thefirst-72-hours-are-critical. [42] FEMA. Fact sheet: Logistics management directorate. http://www.fema.gov/media-library-data/14035423 ̄60 ̄094-562772a6f9b9cf643439d4e92d92225b/Logistics_Management_Directorate_Overview_508.pdf. p3. The Deconstruction of a Relief Material Supply Network and Corresponding Structure Optimization Model WANG Xi-hui, LI Feng, LIANG Liang (School of Management, University of Science and Technology of China, Hefei 230026, China) Along with the increasing frequency of natural and man-made disasters all over the world, the demand for relief supplies has been accelerating in the last decade. When disasters strike a certain area, non-for-profit organizations (NGOs) will purchase relief supplies from suppliers and/or collect donations from donators, then deliver relief supplies to disaster-affected areas to help victims. In practice, however, the relief logistics suffers a serious delay, along with an enormous social and economic loss.The unreasonablestructure of the relief supply is a major reason. Therefore, it’s necessary to study the relief supply network and explore its structure optimization. Towards this end, a complex relief supply network is deconstructed into 8 linear relief supply chains based on the purchase-warehousing-transportation decision-making process. This deconstruction method has three features: (i) completeness, the universal set of all substructures is the general structure; (ii) independence, every substructure is of independence and doesn’t include or affect other substructures; and (iii) integrity, every substructure includes complete process and decisions of a relief effort. Afterwards, a structure optimization model is developed to obtain the optimal combination of relief supply chains to minimize the social loss of a relief operation. The purpose of the model is to obtain the minimum-cost supply chains combination without deteriorating the relief performance or the maximum-performance supply chains combination without increasing the monetary cost. Moreover, the proposed model is verified by the real data acquired from 5.30 YingJiang Earthquake in 2014. Different structure optimization results are compared and analyzed by adjusting parameters or changing external conditions. The comparison and analysis suggest that the types of relief supplies and affected areas have significant effect on the optimal network structure, while the demand quantity of relief supplies has little effect on the network structure. This study clarifies the constitution and process of a relief supply network, which lays the foundation for further improvement. The proposed structure optimization model not only can be used to construct a relief supply network in time for emergency situation, but also provide directional guidance for the construction of relief reserve system. relief supply network; deconstruction; structure optimization; humanitarian operations management 1003-207(2017)01-0139-12 10.16381/j.cnki.issn1003-207x.2017.01.015 2015-10-28; 2016-05-01 国家自然科学基金资助项目(71110107024,71301154,71671169) 李峰(1990-),男(汉族),四川人,中国科学技术大学管理学院,博士研究生,研究方向:应急救灾管理、决策分析,,E-mail: lfeng90@mail.ustc.edu.cn. F252 A4 案例研究




5 结语
