数学教学中培养学生创新能力的实践与认识

常胜彪

摘 要：创新是素质教育的灵魂，如何在数学课堂教学中，培养学生的创新意识、创新能力，已成为数学教育工作者的重要任务之一，教学中要以学生发展为本，多方面培养学生的创新意识，使创新思维成为一种习惯，使学生成为具有创新能力的人。

关键词：数学教学；创新能力；方法

中图分类号：G63 文献标识码：A 文章编号：1673-9132（2017）12-0098-02

DOI：10.16657/j.cnki.issn1673-9132.2017.12.060

一、给学生思考的时间和空间

巴尔扎克曾说：“一个能思考的人才真是一个力量无边的人。”数学是一门思维的科学，需要学生进行比较深刻而抽象的思维活动。因此，在教学中，教师要注意引导学生用数学思维学会思考，这是培养学生创新能力的前提。为了使学生对数学的学习由模仿到创造，这就要使教学过程由封闭走向开放。给学生比较自由、独立和充分的活动机会。

教师要把学习的主动权交给学生，要给学生独立思考的空间。如果对学生管制得太死，就会束缚学生的创造性思维。在教学的过程中，凡是在学生的能力范围之内的，或者经过教师的引导后学生可以自主完成的，就要放开手让学生大胆地去想，去探索，并积极动手操作。在讲授几何课时，要尽量让学生亲自实验，通过量一量、剪一剪、折一折、画一画来探索几何命题。

二、保护学生的好奇心，给学生更多的关爱

爱有利于人的智能发展，有利于激发人的创造力。学生都有强烈的好奇心和好胜心，如果在学习的过程中，他们的这两种情绪一直被有效增强，就会提高学生学习的兴趣，学生容易对学习充满主动性。因此，教师要创造合适的情境，让学生能够在学习的过程中感受到成功的喜悦。这对培养学生的创新意识和创新能力是非常有必要的。比如，我们可以根据学生的性格和爱好，举办几何图形设计大赛、数学笑话晚会、逻辑推理故事演说等等，让每个学生都能找到能够展现自己特长的一个点，在活动中充分地展现自我，找到生活和数学的结合点，从活动中收获快乐的感觉，体会从数学学习中获得的成功，从而培养创新的兴趣。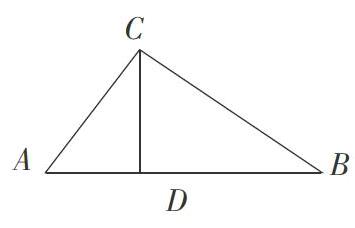

事实证明，爱能激发智力，激发创造力。教师必须爱学生，尤其是对淘气的学生更要爱，在教学中恰如其分地提出问题，让学生“跳一跳，就摘到桃子”，问题是学生想知道的，这样问题会吸引学生，可以激发学生的认知矛盾，引起认知冲突，引发强烈的兴趣和求知欲，学生因兴趣而学，而思维，并提出新质疑，自觉地去解决，去创新。

三、构建新型的师生关系，给学生营造创造性的思维环境

师生关系重建的关键在于对学生权利的尊重。學生虽然人数最多但依然属于学校中的弱势群体，学生个性尤其是独立性、积极性和创造性应当受到尊重和爱护。鼓励学生发表质疑观点是培养学生个性发展的重要环节，课堂上要改变教师“一言堂”的局面，使知识传授成为师生交流的过程。

四、强化学生创新能力训练，培养学生创新的兴趣

培养学生的能力和创新精神必须建立在以知识为载体的基础上，没有知识不可能形成能力，更谈不上有创新精神。教学中，知识的形成与应用的过程都是培养学生能力和创新精神的过程，都应受到重视。 新课程理念特别关注学生的创新精神和创新能力的培养，但是这并不意味着要求教师在超出学生学习和认知水平的基础上，任意加大习题训练的数量和难度，更不能打着提高学生创新精神的名义而使学生丧失学习的兴趣和信心。在教学中，教师要善于营造情境，为学生创造条件，让学生通过生活实践和动手操作来体验数学知识的形成过程和应用。训练题的设计要有层次性，由浅入深，让每个学生都有训练的机会，都得到发展。

五、培养学生的创新思维、创新个性和创新能力

教师运用有深度的语言，创设情境，激励学生打破自己的思维定势，从独特的角度提出疑问。鼓励学生进行批判性质疑。批判性质疑是创新思维的集中体现，科学的发明与创造正是通过批判性质的质疑开始的。在课堂教学中，教师要善于培养学生形成质疑的精神，要大胆对教材，对教师的讲解，对同学的观点，提出质疑，要敢于打破常规，对商榷余地比较大的内容要进行批判式的质疑，并且要勇于寻找合适的途径去验证和解决问题。

总结能力是一种综合素质的体现。因此，在教学中，教师不仅要经常总结自己的教学的得失，而且要善于引导学生进行及时的总结，加强自己做对的，改正自己做错的。长期的总结，能够锻炼学生的集中思维能力。这与培养学生的求异思维是相辅相成的，集中思维使学生准确、灵活地掌握各种知识，将它们概括、提取为自己的观点，作为求异思维的基础，保障了求异思维的广度、新颖程度和科学性。

求异思维又称发散思维，培养发散思维是发展学生数学能力的重要环节。因此，在数学教学中，进行发散思维的训练，是发展思维能力的一条有效的途径。具体做法如下。

（一）条件发散

是指将结论确定以后，尽量变化已知条件，通过从不同角度、用不同的知识解决问题，来发展学生的发散思维能力。

（二）结论发散

是指问题的条件完备，结论不确定，让学生探求所有可能的结论，并通过对问题的求解来发展思维的发散性。例如，下图，在△ABC中，∠ACD=90°，CD⊥ AB于D.问图中存在哪些几何关系，并证明你的结论。

（三）解法发散

即一提多解。一提多解，既可以调动学生的积极性和主动性，又可以拓宽解题思路，培养发散思维能力。

总之，我们不要约束学生的个性发展，不要给他们条条框框，要让学生活起来、动起来要注重点，更要注重面。创造性的活动以丰富的旧知识为基础，以创造性思维能力为核心，以自觉的创新意识为先导，以其良好的个性品质为保证。给学生一片自由的天空，让学生插上想象的翅膀，这样才能有利于创新能力的培养。

参考文献：

[1] 曹玉平.略谈数学教学中创新能力的培养[J].甘肃联合大学学报（自然科学版），2008（5）：80-84.

[2] 戴莹，丁晗.浅析数学教学中培养学创新能力的有效途径[J].吉林省教育学院学报，2009（7）：48-50.