直梁靠模成形变分原理问题的探讨
2017-04-17陈英杰宋锦威吴静瑶
陈英杰 雷 周 宋锦威 吴静瑶
(燕山大学建筑工程与力学学院,河北秦皇岛066004)
直梁靠模成形变分原理问题的探讨
陈英杰1)雷 周 宋锦威 吴静瑶
(燕山大学建筑工程与力学学院,河北秦皇岛066004)
对矩形截面的理想弹塑性直梁在靠模成形过程中边界待定问题,用势能变分原理推导出理想弹塑性材料的靠模悬臂梁弯曲成形的挠曲线方程,从而得到直梁靠模成形的弯曲问题的解.计算表明,推导出的直梁靠模成形的挠曲面方程可应用于工程实际.
变分原理,靠模成形,悬臂直梁,边界条件
塑性成形发展历史可以追溯到1864年,当时法国工程师屈雷斯加(H.Tresca)提出了最大剪应力屈服准则,即屈雷斯加屈服准则[1].较早把塑性理论用于材料成形的是德国的卡尔曼,他在1925年用初等方法分析了轧制时的应力分布[2],其后不久,萨克斯和齐别尔在研究变形过程中提出了相似的求解方法——切块法,即后来的主应力法[3].20世纪50年代中,苏联学者科索夫提出了一个实质上与主应力法相似的近似平衡和近似塑性条件联解法[4].之后应用滑移线理论来求解材料塑性成形问题的方法逐渐增多,英国学者希尔(R.Hill)1950年所著的《数学塑性理论》就反映了这方面的成就[5].直梁靠模弯曲成形问题在工程中经常用到的计算方法有:有限差分法[6]和有限单元法[7-8].它们在工程中得到广泛应用.之后,很多学者又开始研究其他数值分析法求解直梁的弯曲成形问题,如无网格法[9-10]和小波边界元法[11-13].
本文基于材料力学的基本假设,即梁在弯曲变形过程中,截面始终保持为平面——柏努利假设以及剪力及纵向纤维间的侧向应力可以忽略不计.应用势能变分原理对理想弹塑性材料悬臂梁的靠模成形问题进行研究,推导出理想弹塑性材料的靠模悬臂梁弯曲成形的挠曲线方程.
1 梁曲率与截面分布弯矩的关系
如图1所示的理想弹塑性直梁两端受到弯矩作用,h为梁截面高,宽为b.

图1 理想弹塑性材料直梁弯曲示意图
假设该梁的y方向挠度为w,向下为正,则得到挠度与对应应变的关系式
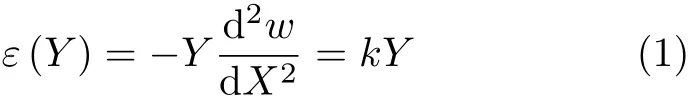
k为梁挠度曲线的曲率:曲率中心在梁轴线上方时为正.横截面弯矩为

随着弯矩值的逐渐增大,界面处于弹性状态,所以

代入式(2),得到


即

式中,ke取正值,对应于ke的弯矩为Me,叫做弹性极限弯矩,σs为极限应力.由式(4)及式(5)可得
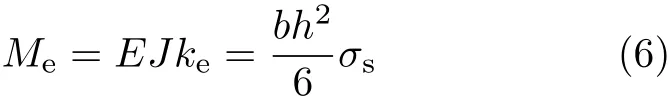
当M>Me时,梁截面的外层纤维的应变继续增大,但应力值保持为σs,塑性区向截面内扩展,设弹、塑性的交界为

在该处,|σ|=σs,于是对应的曲率为
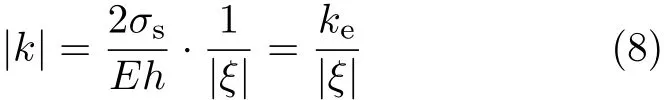
显然,k是ξ的函数,其符号和M相同.与k(ξ)对应的弯矩为

将式(8)代入到式(9)可以得到以下关系式

对于 ξ→ 0时,整个截面会出现全部进入塑性,这个时候,|k|→∞,对应的塑性极限弯矩Ms.由式(10)可得

2 直梁弯曲的基本公式及泛函的变分计算
如图2所示,在上下凹凸模中间的一端固定,另一端自由的理想弹塑性靠模悬臂梁实际系统,计算时可简化为自由端受集中力作用的梁.R为凸模的曲率半径.x1和ξ分别为直梁弯曲变形后的塑性段和弹塑性段长度,余下悬臂段即为弹性区段.当上面凹模向下移动时,可看作在梁的自由端受到一集中力p作用,此时直梁将会发生弯曲变形,在凸模的作用下,直梁的固定端附近会有一段长度为紧贴下面凸模的塑性变形区,该区域称为靠模段.这样靠模段就会形成一个曲率与凸模相同的弯曲变形,随着凹模的向下移动,即p集中力的逐渐增大,直梁便会形成工程中所需要的弯曲成形产品.

图2 靠模悬臂梁系统及其梁截面
对于图2所示的弯曲梁,边界条件待定问题的总势能可表示为
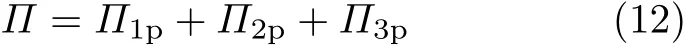
其中Π1p,Π2p和Π3p分别表示直梁弯曲变形后变形能

式中,ke,k1,k2,k3分别为直梁弯曲后在塑性段和弹性段及载荷作用后的曲率.对式(12)取变分极值,则得

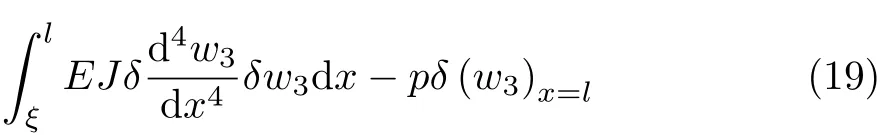
将式(17)和式(19)代入式(16)中,则得

根据变分法预备定理,得欧拉方程和自然边界条件

由式(22)可得
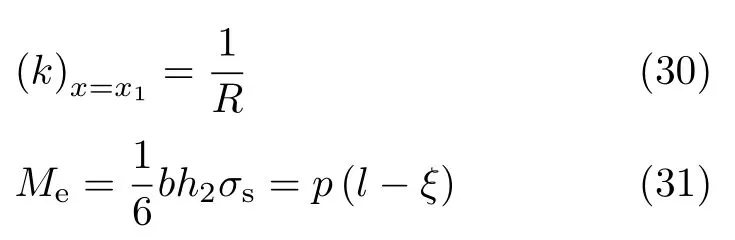
式(31)可得ξ的值.
设

利用x1处挠度和转角的连续条件则得

故有
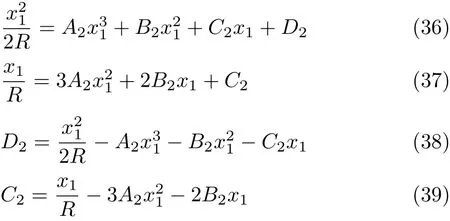
利用x=ξ处的弯矩条件,则得

利用x=ξ处的切力条件,则得


于是有联立方程 (38),(39),(40)和 (44)可分别求得A2,B2,C2,D2表达式

将求得的 A2,B2,C2,D2代入到式 (32)即得 x1≤x≤ξ段的挠曲线方程.
假设ξ-l段的挠曲线为

利用x=l处的静力边界条件,有

于是有
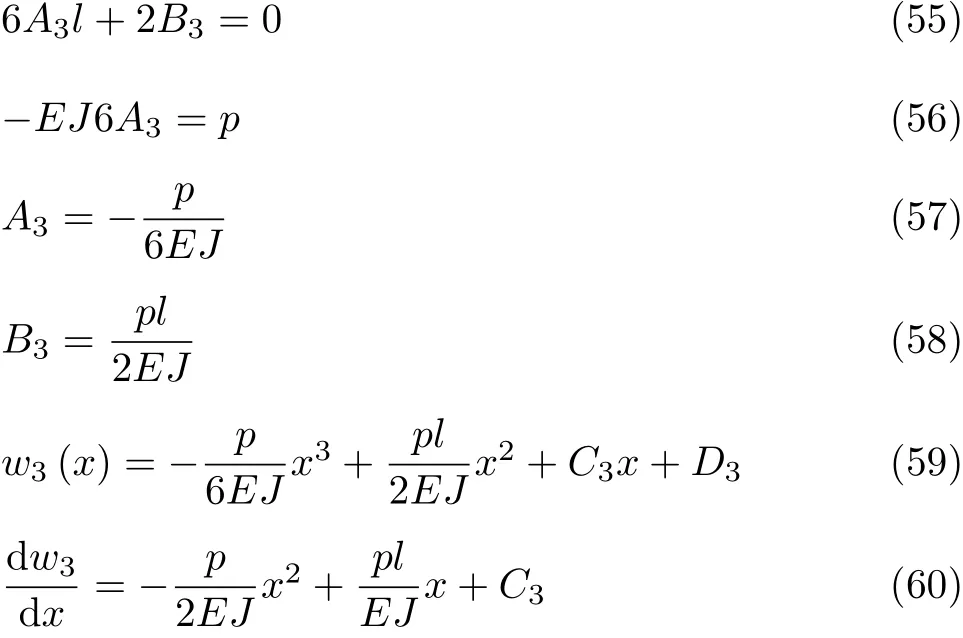
利用x=ξ处的挠度和转角连续条件,则得


则有

联立方程(65),(66)可分别求得C2,D2的表达式

结合式 (59),式 (60),式 (67)和式 (68)便可得到ξ≤x≤l的挠曲线方程.
3 数值计算
选取适当尺寸的矩形截面直梁作为典型计算试件,且将模型中直梁上面的凹模作用简化为在直梁的自由端施加一个竖直向下的集中力.这样既能缩短计算时间,又形象完整地体现了直梁上面凹模的作用.
本文选取长度为 0.5m、截面宽 0.01m、高为0.012m的矩形截面理想弹塑性直梁作为数值算例,模型中直梁下面凸模曲率半径设定1.5m.弹性模量E=206GPa,柏松比v=0.3.在直梁靠模成形的过程中,随着p值的逐渐增大,靠模x1和ξ逐渐增大,且可由式(29)及其式(31)经过Matlab软件编程计算得出具体数值.在靠模x1和ξ之间的弹塑性区段可由式(32)推导出的曲率,经过Matlab软件编程计算得出在该区段靠模直梁各点的纵向挠度值,而在ξ之后的弹性区段可由式(49)得出具体的挠度值.当x=0的截面上出现塑性极限弯矩时有pl=1.5Me,此时p=147N,故当p<147N时,该梁并没有与模具进行接触.表1给出该梁在不同p值作用下对应的靠模段x1和弹塑性段ξ的x轴坐标值.在理论上,人们是无法将一整条梁单纯的用法向载荷使它完全贴伏在下面的凸模上,当然这是指靠近梁自由端的很小一部分.这是因为在自由端上并没有弯矩,这样就无法满足使其端点处那部分紧贴模具时发生的曲率变形所需要的弯矩.因此,本文的p值所取到的上限值为1500N,表2给出了不同集中力p值对应的直梁上各点挠度值.

表1 不同p值对应的x轴坐标值

表2 不同p值对应的梁各点挠度值
本文采用 ANSYS有限元分析软件对一端固定、另一端自由的理想弹塑性靠模成形悬臂直梁进行模拟分析并求解,分层计算所取各节点y方向的挠度值,最后取其算术平均值作为最终变形的y方向挠度值,验证理论计算的准确性.
本文所取节点坐标值x与梁长l的比例分别为0,0.1,0.2,0.3,…,0.9,1.0.沿梁高方向分为2份,共计 3层,沿梁长度方向分为20份,这样方便提取节点坐标值.ANSYS有限单元的模型采用solid45单元.
4 结果分析
前文计算了梁端受不同集中力作用后,弯曲梁在厚度b/2处沿长度方向各点在y方向的挠度理论解以及有限元分析计算值.理论解与ANSYS有限元计算值之间的差率,当p=147N时在x/l=0.1,0.2, 0.3,…,0.9,1.0处分别为 2.8%,2.1%,3.2%,2.6%, 1.5%,1.2%,1.8%,0.2%,1.6%,1%,3%,均在误差范围内,从而验证了本理论推导的正确性,也证明了变分原理应用于理想弹塑性直梁靠模成形计算的可行性.图3给出了不同力作用时梁上各点挠度的理论解与有限元解的分布曲线,两者能够较好地吻合.

图3 不同力作用下b/2截面处的挠度分布曲线
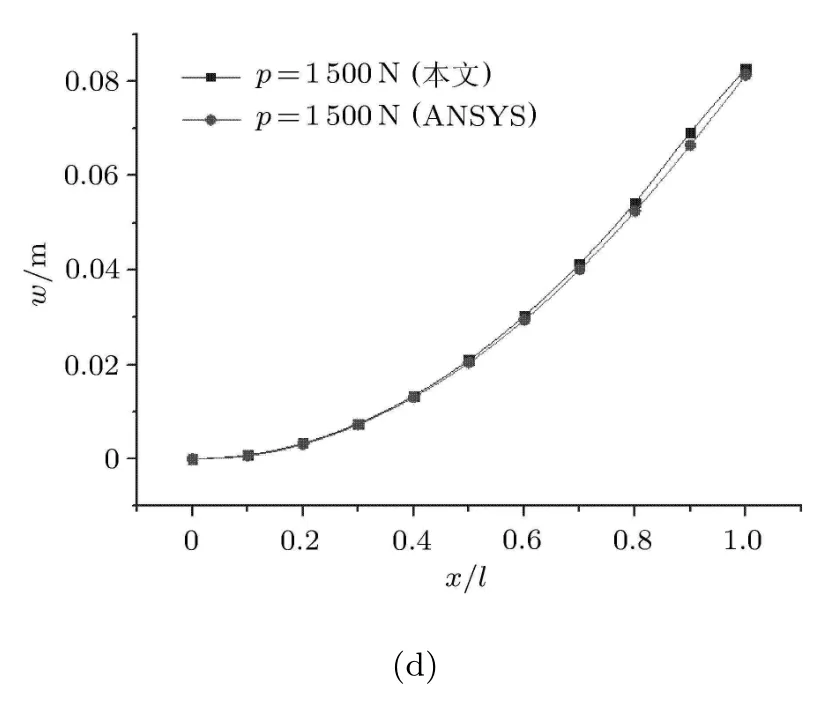
图3 不同力作用下b/2截面处的挠度分布曲线(续)
5 结 论
本文从梁的基本公式出发,应用势能变分原理推导出理想弹塑性材料直梁在靠模成形过程中的挠曲面方程,并在Matlab平台上对其进行计算,得出理论解,同时应用ANSYS有限元分析软件对模型进行模拟分析,并将这两个结果进行比较.比较结果表明:理论推导的结果和有限元解比较一致.
1 Ubbelohde AR.The Molten State of Matter:Melting and Crystal Structure.New York:Wiley,1978
2 Leu DK.Asimplif i ed approach for evaluating bend-ability and springback in plastic bending of an isotropic sheet metals.J Mats Processing Technology,1997,66:9-17
3 Zu FQ,Zhu ZG,Guo LJ,et al.Observation of anomalous discontinuous liquid structure change with temperature.Phys Rev Lett,2002,89(19):94-99
4 Duncan JL,Bird JE.Approxi matecal culations for draw dieforming and their application toaluminumalloy sheet. Metal Forming Plasticity Symposium,Tu-taing Germany, 1978
5 Hill R.塑性数学理论.王仁等译.北京:科学出版社,1966
6 LiuJK,YangY,CaiCW.Convergencestudieson static and dynamic analyses of plates by using the U-transformation and the f i nite dif f erence method.Journal of Sound and Vibration,2006,289(1):66-76
7 Logan DL.A First Course in the Finite Element Method. New York:Thomson Learning,2007
8 Yang Y,Liu JK,Huang PY.Exact convergence studies on static and dynamic analyses of plates by using the double u-transformation and the f i nite element method.Journal of Sound and Vibration,2007,305(122):85-96
9 王辉,刘伟.梁弯曲问题的无网格解法.中原工学院学报,2008, 19(2):69-71
10 Xiao JR,McCarthy MA.Meshless analysis of the obstacle problem for beams by the mlpg method and subdomain variational.European Journal of Mechanics Solids,2003, 22(3):385-399
11 杨德全,赵忠生.边界元理论及应用.北京:北京理工大学出版社,2002
12 苏甘龙.梁弯曲问题的样条小波边界元法.厦门理工学院学报, 2008,16(4):57-62
13 何正嘉,陈雪峰.小波有限元理论及其工程应用.北京:科学出版社,2006
(责任编辑:刘希国)
THE VARIATIONAL PRINCIPLE FOR A PROFILING FORMING STRAIGHT BEAM
CHEN Yingjie1)LEI Zhou SONG JinweiWU Jingyao
(College of Civil Engineering and Mechanics,Yanshan University,Qinhuangdao 066004,Hebei,China)
Based on the variational principle of unknown boundaries formed in the forming process of an ideal elastoplastic straight beam of rectangular section,this paper carries out the variational calculation of the potential energy to derive the deflection curve equation of a cantilever beam bending mode,and to obtain the solution to the bending of the prof i ling forming straight beam.According to the calculation results,the deflection equations of the prof i ling forming straight beam can be derived with the application of the variational principles of potential energy and complementary energy.
variational principle,prof i ling forming,straight cantilever beam,boundary conditions
O343
A
10.6052/1000-0879-16-234
2016-07-11收到第1稿,2016-09-08收到修改稿.
1)陈英杰,教授.E-mail:cyjysu@ysu.edu.cn
陈英杰,雷周,宋锦威等.直梁靠模成形变分原理问题的探讨.力学与实践,2017,39(1):61-67
Chen Yingjie,Lei Zhou,Song Jinwei,et al.The variational principle for a prof i ling forming straight beam.Mechanics in Engineering,2017,39(1):61-67
