65°三角翼亚音速复杂流场计算和数据可视化1)

李 立

(中国航空工业集团公司西安航空计算技术研究所，西安710065)

应用研究

65°三角翼亚音速复杂流场计算和数据可视化1)

李 立2)

(中国航空工业集团公司西安航空计算技术研究所，西安710065)

提出一种基于非结构混合网格和有限体积法的有效计算策略，对第二期国际涡流试验项目(second international vortex flow experiment,VFE-2)的尖前缘65°三角翼在马赫数0.4，迎角20.3°，雷诺数2×106条件下的亚音速复杂流场结构进行数值模拟，重点探讨了基于计算数据进行该类型复杂涡系干扰表面和空间流场关键特征提取和数据可视化问题.通过与相关试验类比，建立了与先进试验流动显示技术相比拟的定性和定量分析方法，为三角翼这类复杂流场结构的精细分析奠定了技术基础.采用上述方法，细致分析了亚音速三角翼的大迎角复杂旋涡流场结构，得到了与试验一致的结论.研究证实：在大迎角条件下，三角翼流动物理复杂，黏性效应耦合严重，只有通过N-S方程计算才能准确地捕捉主涡和二次涡的发展.

数据可视化，混合网格，有限体积法，旋涡运动，VFE-2(second international vortex flow experiment)三角翼

Key wordsflow visualization,hybrid mesh,f i nite volume method,vortex flow,VFE-2(second international vortex flow experiment)delta wing

三角翼是现代战机及无人机的常见布局形式，具有深刻的工程应用背景.在亚音速条件下，绕三角翼的流动是典型的几何简单，但物理形成机制复杂的旋涡流动.在不大的迎角下，三角翼将在上翼面形成前缘分离涡，并随着迎角增加不断增强；当迎角超过一定限度后，旋涡从稳定发展为不稳定，直至从后缘逐步发生涡破裂.涡破裂对飞机气动特性影响非常明显，严重情况下，会对飞机的操纵性和稳定性带来致命影响.为此，在过去数十年间，各国都设立了相关项目对三角翼的旋涡结构及形成机理开展研究，其中尤以美国和欧盟联合发起的第二期国际涡流试验项目(second international vortex flow experiment,VFE-2)最为知名[1].VFE-2项目的重要价值在于通过发展光学压敏测量技术(pressure-sensitive paint technique,PSP)、粒子影像测速仪技术(particle image velocimetry technique,PIV)等先进试验手段，测量得到VFE-2系列三角翼模型的表面流场和空间流场精细试验数据[2]，为CFD软件的对比分析和结果确认提供了丰富的资源.

近年来，数值计算已在飞行器设计中得到广泛应用.采用数值方法进行流场分析的一个巨大优势是能够获得比试验多得多的流场信息.但选取哪些数据来进行流场分析和进行直观的流动显示，具有一定的挑战性.由于不同的流动往往具有不同的流动特征，因而针对不同问题不大可能采用完全相同的流动分析和显示方法来统一处理.最恰当的办法应是针对不同流动的物体特征，研究建立适当的关键流动特征提取方法.基于这一考虑，本文采用混合网格策略和有限体积法，数值求解了VFE-2尖前缘65°三角翼在马赫数0.4，迎角20.3°，雷诺数2×106条件下的亚音速流场.以此为基础，重点探讨基于计算数据如何进行该类型复杂涡系干扰表面和空间流场关键特征提取和数据可视化，获得与先进试验手段(测压、油流、PSP、PIV等)相比拟的数据可视化方法和结果，从而为三角翼这类复杂流场结构的精细分析奠定技术基础.

1 数值方法

1.1 控制方程及求解

控制方程为雷诺平均 N-S(Reynolds-averaged Navier-Stokes,RANS)方程，守恒形式如下

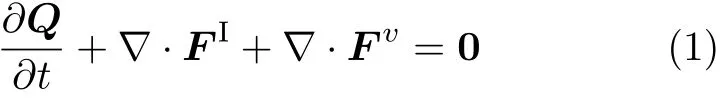
其中

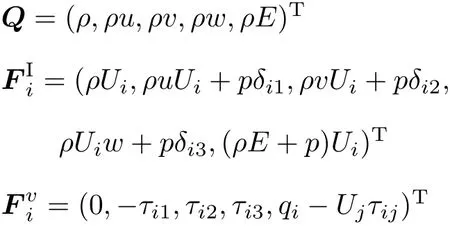
这里，ρ,U=(u,v,w)T,E,p,τij,qi分别表示密度、速度矢量、总内能、压强、黏性剪切应力张量和热流;δij表示Kronecker函数,δii=1,δij=0(i/=j).剪切应力张量可根据Boussinesq假设，表示为

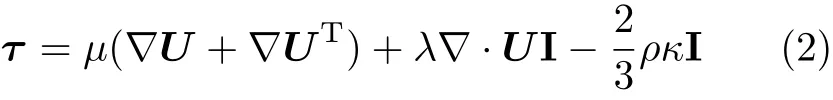
式中，µ为黏性系数，为层流部分µl和湍流部分µT之和,µ，κ为湍动能,I为单位矩阵.压强根据状态方程计算，对理想气体有

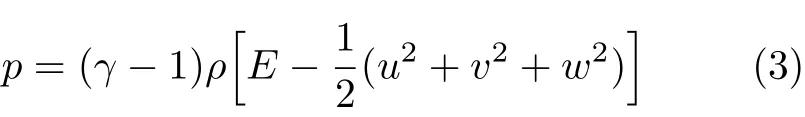
式中，γ为比热比，对空气，γ=1.4.

湍流模型方程采用Spalart-Allmaras(SA)一方程模型[3].相对其他复杂的湍流模型，SA一方程模型具有计算效率高、鲁棒性好、对分离流动的模拟精度高等优点，是航空工程领域应用最广泛的湍流模型之一.为了改善计算的实际收敛性能，本文还引入了涡量修正技术，即将模型方程的涡量值修正为

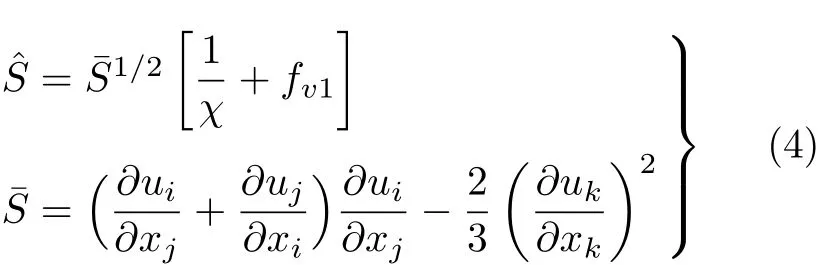
式中，fv1=χ3/[χ3+(0.71)3],χ=ρˆv/µl,ˆv为SA方程的求解变量.

对方程(1)，本文采用非结构混合网格策略和有限体积法进行数值求解.目前，利用非结构网格进行有限体积离散主要有两种方式.一种直接采用网格单元作为控制体，称为格心(cell-centered)格式；一种以网格单元顶点为中心，采用对偶网格方法建立控制体，称为格点(cell-vertex)格式.两种方式各有优劣，一般说来，格点格式效率比格心格式要高[4].本文选用格点格式.如图1所示，对每个网格单元的节点，虚框包围部分是实际控制体.由式(1)，在每个控制体上求体积积分，并运用Gauss公式，可得

具体计算采用Jameson等[5]提出的标准中心差分格式进行空间离散，并采用3阶总变差Runge-Kutta方法进行时间推进求解.计算过程中，使用了当地时间步长、隐式残值光顺及聚合多重网格技术等进行计算加速[6].

图1 格点格式有限体积法的控制体构造

1.2 计算模型及网格

计算模型是VFE-2尖前缘65°三角翼，模型外形和几何定义参数定义见参考文献[2].VFE-2项目2004年由美国和欧盟联合发起，采用不同前缘钝度的三角翼模型作为研究对象，旨在为CFD软件对复杂涡流场的预测能力评估提供可靠的试验数据.对该系列三角翼模型，NASA在1996年已先期开展了大量试验研究，提供了在较大范围雷诺数和可变马赫数状态下的表面压力分布、法向力、俯仰力矩系数等试验数据[7].与NASA早期的试验不同，VFE-2项目偏重于进行精细风洞试验.试验在德国的德-荷风洞机构的跨音速风洞中进行，采用PSP和PIV等更先进试验手段，提供了在不同马赫数、不同雷诺数状态、不同迎角范围内的详细、可靠的流场数据[2].本文选取M∞=0.4,α=20.3°,Re=2.×106的状态开展研究.该状态接近于涡破裂的临界状态，对软件能力的要求较高[8].

为了节省计算量，全部计算基于半翼展模型(半模)展开.采用的计算网格自主生成，物面和空间网格均采用网格自适应技术进行了加密以提高边界层、分离区及剪切层的模拟精度[9-11].如图2所示，计算区域沿流向的远场边界取为50倍弦长，沿展向的远场边界取为20倍弦长.边界层内第1层网格达到5.0×10-6弦长.半模网格总的网格点数约为65万，总的网格单元数约为170万.计算中，远场均采用无反射特征远场边界条件，物面均采用无滑移绝热壁面边界条件.

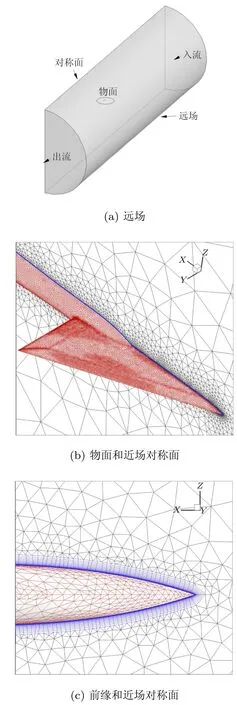
图2 三角翼模型的计算网格

2 计算结果及数据可视化分析

2.1 表面流场的流动显示

对于试验而言，用于表面流场的试验流动显示技术主要包括油流试验技术和PSP等.通过计算数据对油流试验、PSP等试验技术进行复现，相对比较容易.

对油流试验结果，计算可以通过绘制极限流线的方式来复现.按照定义，极限流线是流线无限接近物面时的一种极限状态.为了通过计算数据进行极限流线绘制，本文采取的具体步骤是：首先抽取物面网格、第1层边界层网格及相应的解数据(速度场)形成独立的数据集；然后针对该数据集进行流线绘制即得到极限流线.根据极限流线结果可以清晰判定流场的分离和再附.图3给出采用本文RANS方法计算得到的极限流线结果.由图可知，该三角翼构型在选定状态下发生明显二次分离，主涡和二次涡附着线清晰可见.

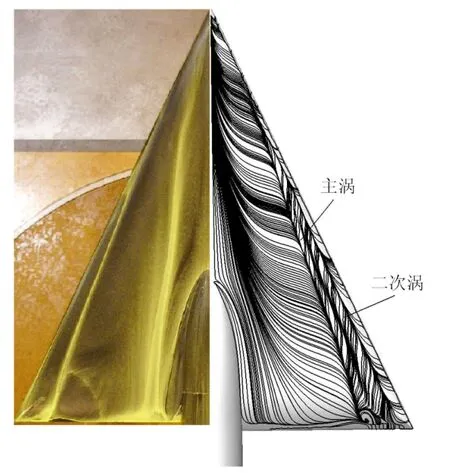
图3 计算对油流结果的复现

PSP是试验中实时观测三维流动现象的有用工具，试验观测结果为表面压力系数分布.因此，计算可以采用绘制压力系数分布云图的方式来复现.此外，由于计算不像试验受物理条件限制，根据需要还可以显示其他变量的分布云图，其效果等同于PSP.对传统PSP显示进行复现的方法过程为：首先，根据式(3)，可以由守恒量直接计算压强；然后，根据压力系数定义可得

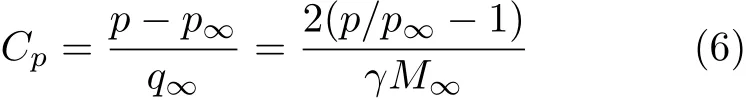
这里，q∞为自由流动压，p∞为自由流压强,M∞为来流马赫数.根据表面压力系数分布可以清晰判定三角翼前缘涡在物面留下的印迹，并能定性和定量分析出吸力峰的位置.图4给出本文计算得到的PSP结果与试验结果[12]的对比.作为比较，同时给出Euler和RANS计算的不同结果.图中，低压区即是前缘涡在物面留下的印迹.在图4的结果中，计算比试验给出的低压区更清晰，主要是由于对计算结果进行数据可视化时对压力系数分布区间作了特殊处理.可以看出，Euler计算给出的主涡低压区从机翼顶点一直拓展到约80%弦长位置，之后发生压力陡增.物面压力分布的陡变实际上反映出涡的破裂.与Euler结果相比，RANS计算与试验给出的结果更加接近，其主涡低压区一直拓展到尾缘附近，没有发生压力陡增，表明在选定亚音速条件下，主涡没有发生涡破裂.推测造成Euler计算与RANS计算结果差异大的主要原因是，三角翼边界层黏性效应干扰严重，Euler计算由于忽略了物理黏性影响，造成涡远离壁面后很快被耗散掉，因而提前发生涡破裂.从图4的计算结果还可看出，Euler和RANS计算存在一个显著的区别是后者能够准确预测出前缘和主涡之间的二次涡.图4中试验结果和RANS计算结果给出的前缘与主涡之间存在模糊的低压痕迹直接反映的就是二次涡.这再次说明，对三角翼这类复杂涡流场，RANS计算结果明显优于Euler计算.与Euler计算结果相比，RANS计算给出的主涡和压力吸力峰位置明显更靠近翼根，与试验结果相符.

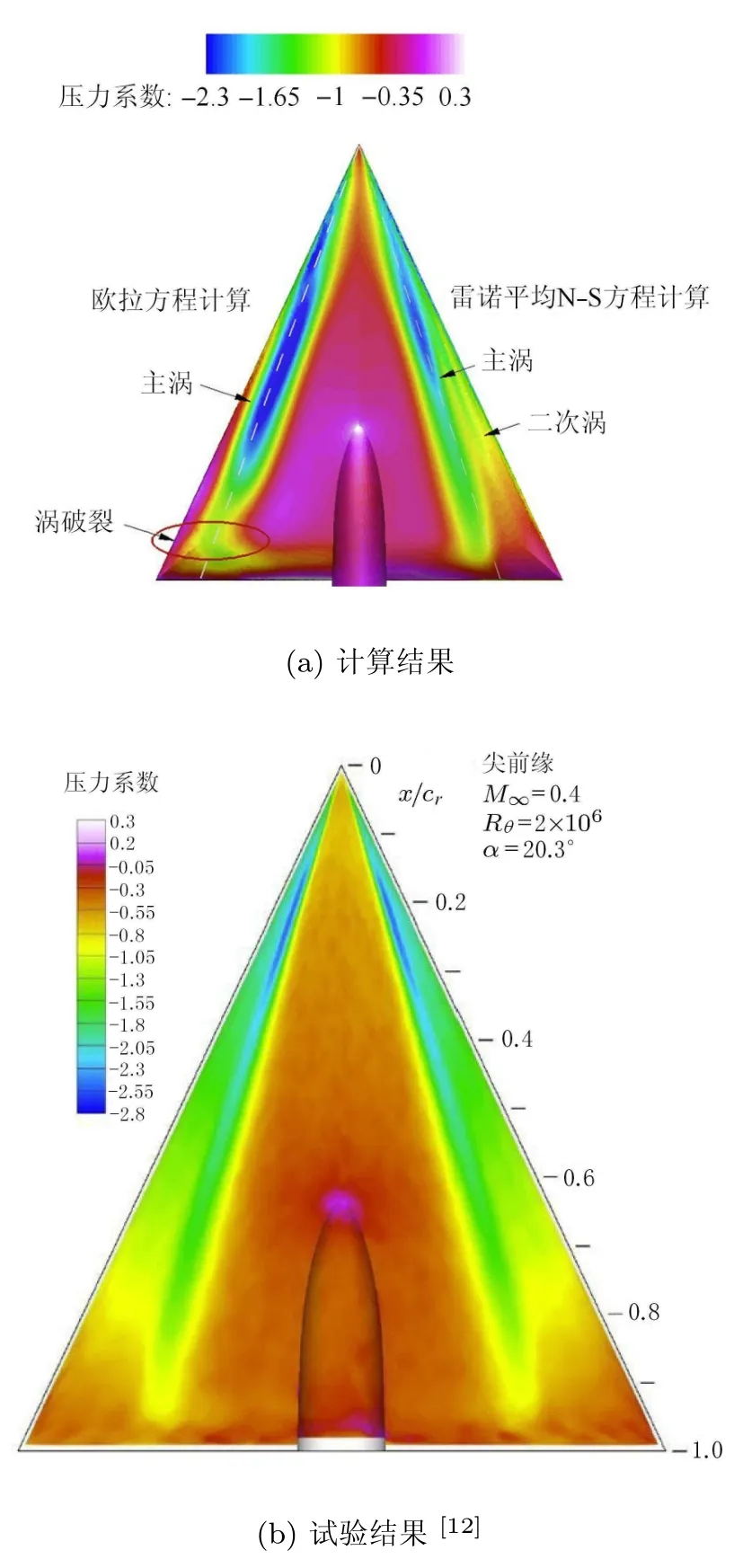
图4 计算对PSP结果的复现

根据PSP结果，可以进一步进行定量比较.图5和图6分别给出沿主涡涡核及沿流向不同横向截面的压力系数分布比较.图5的结果进一步证实了对图4的分析，Euler计算会发生明显的压力陡增.图6的结果表明本文RANS结果与试验结果、文献计算结果[10]符合较好，沿流向60%弦长之后的压力吸力峰位置、强度结果均优于文献.

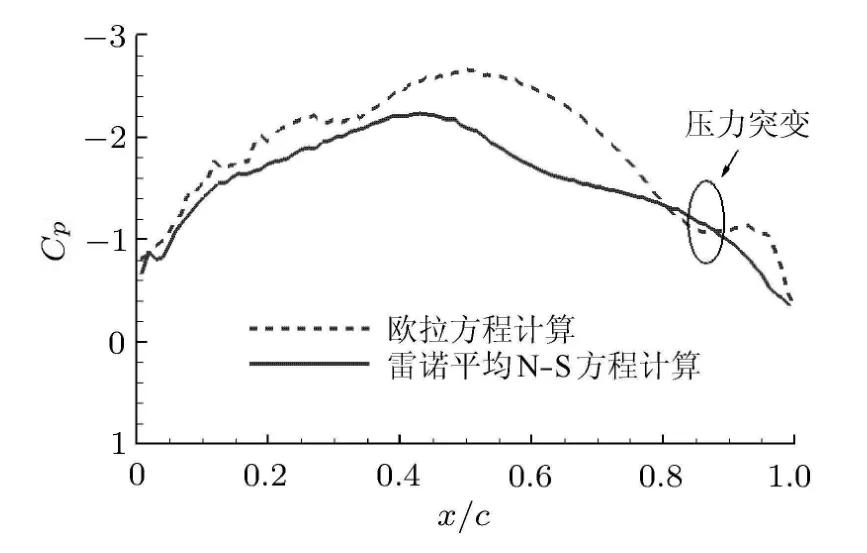
图5 沿主涡涡核的压力系数分布比较(c为平均气动弦长)

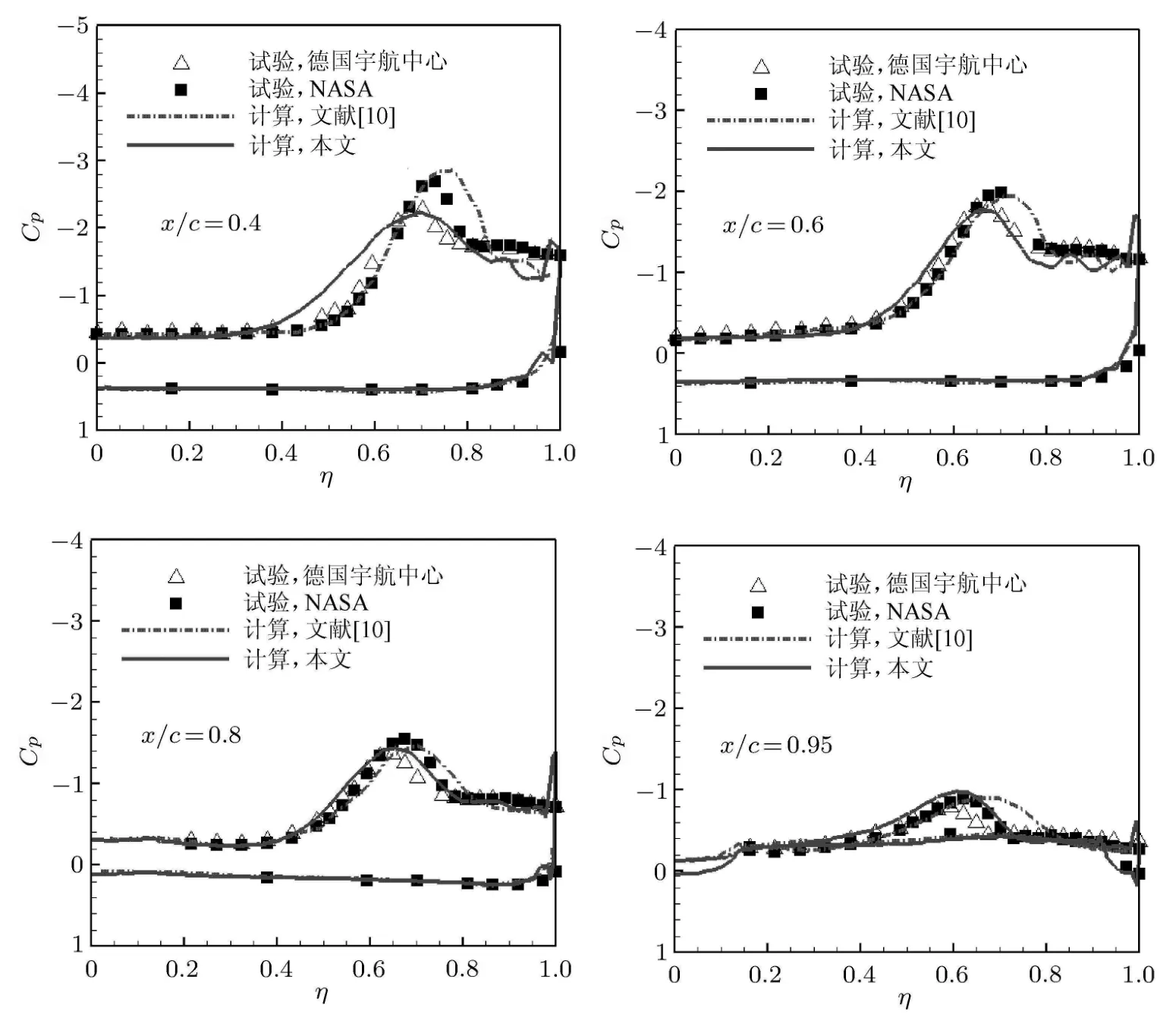
图6 横向截面压力系数分布比较

2.2 空间流场的流动显示

试验中，用于空间流场流动显示的主要技术是PIV技术.PIV技术从20世纪80年代开始发展，最早用于应力测量，但由于它能在不干扰流场的情况下，获得整个瞬时以及时均的速度场，并可以进一步得到涡流场等参数，很快在流场测量中得到广泛应用.在流场测量中，PIV给出的结果主要是不同截面位置的速度矢量场.图7给出本文RANS计算在x/c=0.7站位对PIV测量速度场[13]的复现结果.可以看到，计算得到速度场所反映的关键流动特征与试验基本一致，在机翼上方存在明显的高速流动分离区，而在翼尖呈现明显的低速回流区.图8进一步给出沿流向不同站位的典型速度流场，清晰反映出三角翼上方主涡分离区沿流向方向的发展.与压力云图反映出的流场特征一样，该三角翼在选定状态沿流向方向直至80%弦长位置仍没有发生涡破裂.

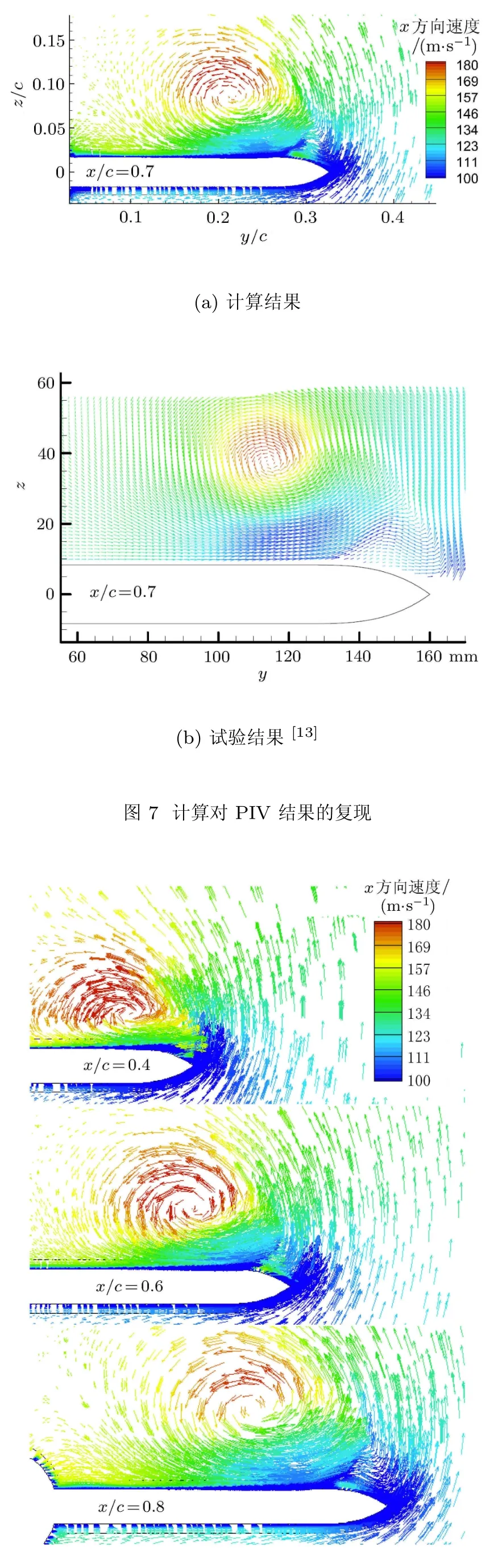
图8 三角翼沿流向方向不同站位的速度流场

值得指出，与试验相比，由于计算结果包含了更完整的流场信息(密度、压强、速度等)，因此通过这些信息很容易得到用户所关心的、更丰富的物理场.对于亚音速三角翼这类复杂涡流场，主要关心两个问题：(1)涡核的计算；(2)设计何种物理量作为关键特征量以进行更清晰、更直观的空间流场展示.问题的实质是，需要进行空间流场关键特征的提取.借鉴课题组在复杂涡流场网格自适应探测器设计方面的经验[9]，对三角翼涡流场关键特征的提取，本文提出以下具体思路.

涡核计算可采用对速度梯度张量进行特征值分析的方法.步骤如下：(1)对网格单元的每个节点进行速度梯度张量的计算Aij=(∂Ui/∂xj),i,j= 1,2,3；(2)进行速度梯度张量的特征值分析，得到相应的特征值及特征向量(λi,xi),i=1,2,3；(3)判断该组特征值是否由一个实特征值及一对共轭的复特征值组成；如是，则把该节点标记为涡核.

关于三角翼涡流场关键特征变量的定义问题，很显然，选择并不唯一.传统方法中常把涡量作为反映涡强度及发展的物理量.通过对涡流场特点的分析，结合反复实践和对比研究，发现，总压比、熵估计及湍流涡黏性这几种物理量均是能较好反映涡发展的空间流场关键特征量.总压比和熵估计的定义式分别为

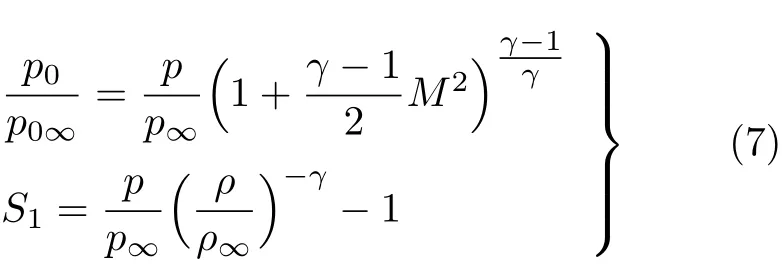
式中，M为当地马赫数.

图9给出对三角翼流场进行特征提取和流动显示的典型结果.采用在截面进行空间流线投影的方式对涡的发展进行展示，并采用湍流涡黏性、总压比作为关键特征物理量进行空间流动显示，清晰显示出空间上翼尖涡的发展.空间流场结果显示，本文计算准确捕捉到空间上二次涡的发展.从这一流动显示结果可反映出，相对于试验，计算在数据完备性方面具有天然优势.

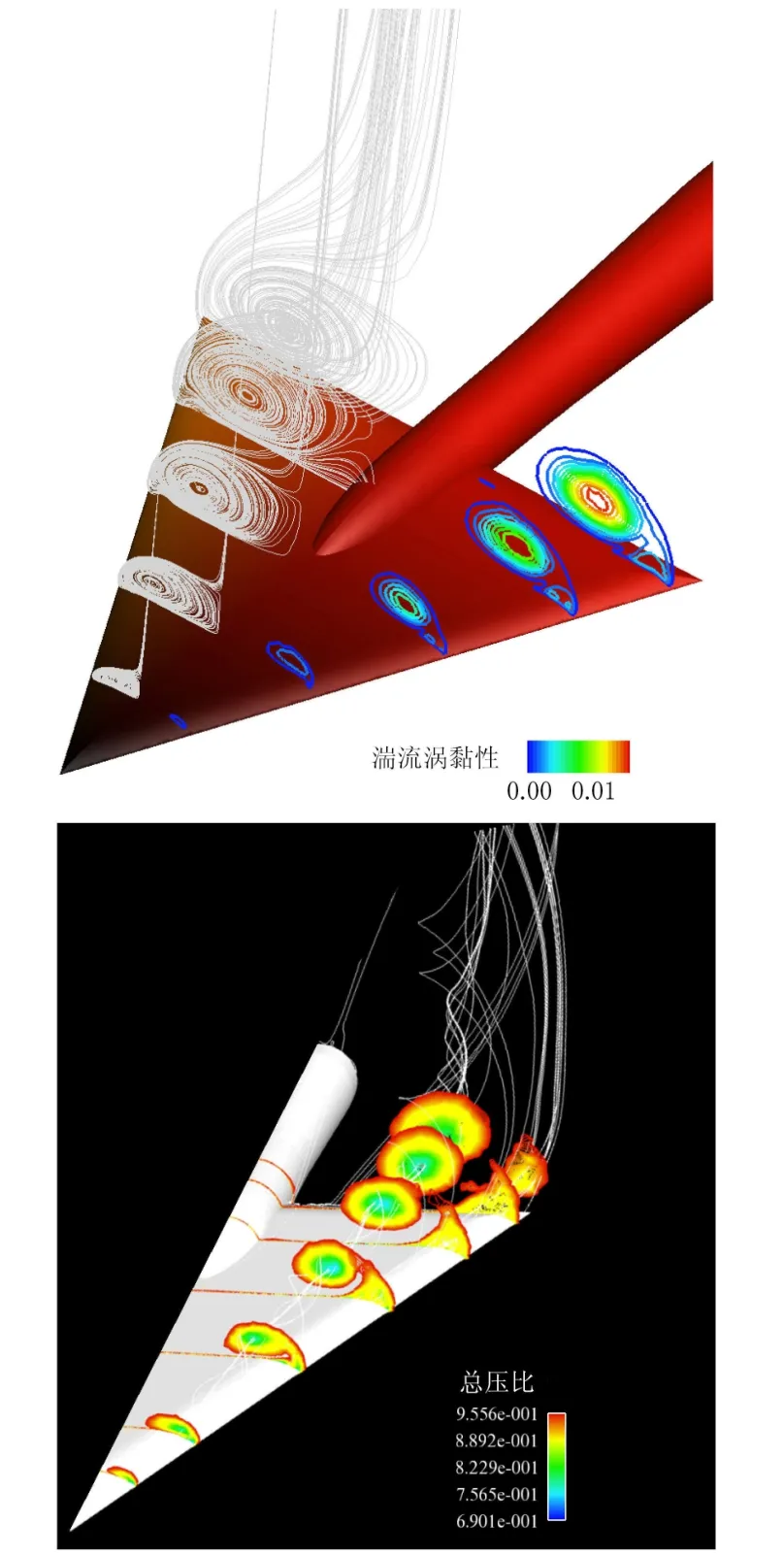
图9 三角翼空间流场关键特征提取和空间流场显示

3 结 论

本文提出采用非结构混合网格策略和有限体积法对65°VFE-2尖前缘三角翼进行数值计算.结合与试验流动显示技术对比，开展了该类型复杂流动的数值流动显示方法研究，为三角翼这类复杂流场结构的精细分析奠定了技术基础.通过本文研究，形成主要结论如下：

(1)与试验相比，数值计算在数据完备性方面具有天然优势，能够完美复现典型试验流动显示技术(如油流、PSP、PIV等)，并能丰富传统流动显示技术的内涵.

(2)本文计算准确预测了尖前缘三角翼在亚音速大迎角条件下复杂的旋涡流场结构.计算表明，亚音速三角翼涡流场的黏性效应严重，采用RANS计算能够准确捕捉到主涡、二次涡的发展，而Euler计算对涡的精细捕捉能力明显不足，过度预测主涡的发展.

(3)流场关键特征的提取是流动显示和数据可视化分析的关键问题.对三角翼复杂涡流场而言，除了传统方法中常用的涡量外，实践表明，总压比和熵估计也均能很好地展示涡强度及涡的发展.

致谢：本文VFE-2项目试验数据由德国宇航院授权使用，在此表示感谢.

1 Hummel D,Redeker G.A new vortex fl ow experiment for computer code validation.RTO AVT Symposium on Vortex Flow and High Angle of Attack Aerodynamics,Loen, Norway,2003

2 Konrath R,Klein C,Schr¨oder A.PSP and PIV investigations on the VFE-2 con fi guration in sub-and transonic fl ow.46th AIAA Aerospace Sciences Meeting and Exhibit, Reno,Nevada,2008

3 Spalart PR,Allmaras SR.A one-equation turbulence model for Aerodynamic fl ows.La Recherche Aerospatiale,1994, (1)：5-21

4 阎超,于剑,徐晶磊等.CFD模拟方法的发展成就与展望.力学进展,2011,41(5)：562-588

5 Jameson A,Schmidt W,Turkel E.Numerical solutions of the Euler equations by fi nite volume methods using Runge-Kutta time stepping scheme.AIAA Paper 81-1259,1981

6 朱培烨.三维非结构网格的欧拉方程聚合多重网格法.航空计算技术,2004,34(3)：6-9

7 Chu J,Luckring JM.Experimental surface pressure data obtained on 65°delta wing across Reynolds number and Mach number ranges.NASA Technical Memorandum 96-4645,1996

8 Fritz W.What was learned from the numerical simulations for the VFE-2.AIAA Paper 2008-399,2008

9 Bai W,Qiu Z,Li L.Recent e ff orts to establish adaptive hybrid grid computing capability at ACTRI.Computational Fluid Dynamics Journal,2007,15(4)：438-449

10 Pirzadeh SZ.Vortical fl ow predication using an adaptive unstructured grid method.RAT AVT Symposium on Advanced Flow Management：Part A-Vortex Flows and High Angle of Attack for Military Vehicles,Loen,Norway,2001

11 李立,白文,梁益华.基于伴随方程方法的非结构网格自适应技术及应用.空气动力学报,2011,29(3)：309-316

12 Konrath R,Klein C,Engler RH,et al.Analysis of PSP results obtained for the VFE-2 65°delta wing con fi guration at sub-and transonic speeds.44th AIAA Aerospace Sciences Meeting and Exhibit,Reno,Nevada,2006

13 Konrath R,Schr¨oder A,Kompenhans J.Analysis of PIV results obtained for the VFE-2 65°delta wing con fi guration at sub-and transonic speeds.24th Applied Aerodynamics Conference,San Francisco,California,2006

(责任编辑：刘希国)

NUMERICAL SIMULATION AND VISUALIZATION OF COMPLEX SUBSONIC FLOW OVER A 65°DELTA WING1)

LI Li2)
(AVIC Aeronautics Computing Technique Research Institute,Xi’an 710065,China)

The VFE-2 65°delta wing with sharp leading edge in subsonic flows at Mach number of 0.4,angle of attack of 20.3°,and Reynolds number of 2×106is numerically simulated by using an unstructured hybrid mesh based f i nite volume method,with emphasis on how to extract the key flow features for visualization both on surface and in space for such type of complex flows.Approaches for the advanced flow visualization techniques are used for qualitative and quantitative analyses,as a solid foundation for elaborated analysis of complex flow structures of delta wing.With these approaches,the complex vortex flow structure of the subsonic delta wing at high angle of attack is analyzed,and results are consistent with experiments.It is shown that the flow over delta wing at high angle of attack has a complex physical nature with a strong viscous coupling ef f ect,and the evolutions of the primary and secondary vortices can be accurately captured only by a Navier-Stokes equation based simulation.

V211.3

A

10.6052/1000-0879-16-195

2016-06-12收到第1稿，2016-07-07收到修改稿.

1)国家863计划(2012AA01A304)和航空科学基金(2015ZA31002)资助项目.

2)李立，高级工程师，研究方向为计算流体力学.E-mail：westlili@163.com

李立.65°三角翼亚音速复杂流场计算和数据可视化.力学与实践,2017,39(1)：18-24

Li Li.Numerical simulation and visualization of complex subsonic flow over a 65°delta wing.Mechanics in Engineering,2017,39(1)：18-24