巧设过渡环节，促使资源生成

吴丽红

在小学数学课堂教学中，每一个教学环节的过程都需要有一定的情境或语言的连接，恰当的情境、严谨的语言过渡可促使有效学习活动的进行。小学数学知识具有严谨性、系统性、逻辑性，每课时各知识间不仅具有系统性，且各章节乃至整个小学阶段各部分知识也是前后贯穿、互相联系的。因此，教学中情境创设的过渡和教师语言的过渡显得尤其重要，教师不仅要对知识之间的联系性、系统性、逻辑性做到了如指掌，而且在教学过程中更应体现以下几个方面。

一、搭建从无到有的情境，让学生思维拾级而上

教学中，搭建从无到有、从未知到已知、从不理解到理解的教學情境，对数学概念、性质、规律等的知识构建尤其重要。因此，教师要从学生学习数学的心理和认知规律的角度，搭建从无到有、从未知到已知、从不理解到理解的教学情境，充分让学生理解数学的概念、性质、规律等形成的原因和背景。这不仅需要有效的教学情境，更需要从无到有的教学环节之间过渡性语言的引领，使环节间自然流畅，让学生的思维拾级而上。

如“空间与图形”中的“直线、射线、线段”的教学，教师可以让学生在纸上移动笔尖，画出以下各种各样的线。如：

在教学时，教师可以根据学生画出的多种线，适时启发：“哪些线是直线？那些线是曲线？你能把这些分类吗？你用什么方法得到图中的直线、射线和线段？”

教师运用了语言和图形相结合的方法进行阐述，学生通过自己动手操作或想象使静态的“点”通过自由运动将图形动态化，并画出来。最后，教师用计算机演示点的运动，让学生观察点的运动形成一条线的过程。学生思维积极，较好地掌握了直线、射线和线段的特征。这归功于教师的过渡语“你能把这些线分类吗？你用什么方法得到图中的直线、射线和线段？”的引导作用。这样的教学过程，让学生经历了“观察—点的运动过程—想象（形成线的表象）—应用（画出运动后形成的线）”这样的过程，对培养空间想象起到了积极的作用。

二、注重由错到对的启迪，让学生错误及时拨正

错误是课堂教学中一种有价值的资源，正是因为有错误资源的产生，才需要教师的引导和启发，更需要学生从内心深处产生一种质疑探究的欲望。这时，教师的过渡性语言就显得尤为重要，教师能在产生错误这个环节上积极启发和提示，尤其是对学生的错误的拨正有一个“由远及近”的动态过程。因此，在教学过程中，教师的过渡性语言能点拨出错误信息的思考空间，让学生思维“由远及近”步入思维的最佳状态，以便教师了解学生的真实想法，并抓住契机和闪光点将问题探究进行到底。

如在教学“把整数、假分数化成带分数”一课时，学生在学习了整数化假分数之后，从练习中发现，学生对于3= 这样的题目计算时往往容易混淆。学生通常会出现这样的两种情况：3= 和3= 。

教学中，教师应不急于评判，而是把发言权交给学生：“你认为谁的答案正确？”此时，学生议论纷纷，有的学生迫不及待地发言：“分子应该是3×12=36。”此时，教师追问：“为什么是3×12=36呢？你的根据是什么？”有的学生想到：“求分子 ，即求除法中的被除数，用除数乘以商。”教师继续追问：“这里哪来的除数和商？”学生纷纷解释道：“除数相当于分母，商相当于整数，所以分母乘整数等于分子。”

学生在求解这类题目时，由于受知识经验和方法的局限出现一些错误是正常的，这些错误恰恰是学生思维本身的表现，需要学生有一个自我否定、自我纠错的过程。这时，教师应及时抓住课堂中出现的这种“不和谐音符”，巧用它们为学生搭建自我探究的平台，不断启迪，及时纠正。而在这个环节中，教师的过渡语言的启迪，恰好是纠错过程的“润滑剂”和“催生剂”。这样，课堂上出现了让人记忆深刻的闪光点，将教学中产生的“错误资源”拓展为更有效的教学资源。

三、创设认知冲突情境，让学生乐于发现问题

众所周知，小学生的认知特点是由具体到抽象、由低级向高级发展的过程。在新知的学习过程中，怎样让学生的思维走到深处，这不仅需要教师寻找情境与教学内容、教学目标和谐一致的共生点，也需要合理通过过渡预设问题，更需要教师在教学过程中根据学生的认知特点创设情境，产生认知冲突，同时在已有知识环节上设计好过渡性语言，引导学生在已有知识经验与新知学习任务间形成认知冲突，建立起一个助引学习的策略，推进学生发现问题，深入思考，提升新知掌握的深刻性。如在教学“中位数”一课时，教师提问：“六年级一班进行体育跳绳测试，在规定时间内，小亮跳了110下，他所在的小组平均跳了117下，小亮的跳绳成绩在本小组中处于什么位置？”

大部分学生都认为，既然小亮跳绳的成绩比平均数低，他在小组中一定处于“中下水平”。这时，教师并不急于结论，而是通过过渡性语言在这个环节上设计了一个表格式的情境，让学生观察，给学生带来巨大的认知冲突。即：“高于平均分属于中等水平，低于平均分属于中下水平，是这样吗？请看下面这个小组跳绳的成绩（如表1所示）”。

这时，教师问：“看了这张表格你有什么想法？小亮的成绩在小组中排列第几？”

学生们经过分析，发现平均数也有“失灵”的时候，教师通过这个问题，让学生深刻体会到中位数的意义。教学中，教师没有直接呈现中位数的概念，而是先利用学生的认知冲突创设情境，再通过渡性语言“高于平均分属于中等水平，低于平均分属于中下水平，是这样吗？”创设了冲突情境，以“平均数”为参照物，让学生认知冲突，最后引导学生发现问题，把问题本质反映出来，引出“中位数”概念，从而使学生对“中位数”的理解更加深刻。

四、巧设过渡语言环节，让课堂结尾亮出精彩

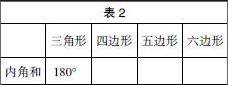
学生从上一个环节得到的数学知识技能和数学活动经验往往会直接或间接地影响到下一个环节的学习上，上一个环节中所产生的学生元认知，会让学生更深入思考，使所学的知识更具系统性。因此，教师在结尾的过渡性语言应从新认知中诱发生长点，为学生营造一个思考的转折点是至关重要的。如在教学“三角形的内角和是180°”的课堂上，课尾可以设计这样的过渡性语言：“本节课你们学习了什么知识？你们都会运用这些知识解决问题吗？请看下表（如表2所示），你会做吗？”

三角形 四边形 五边形 六边形

内角和 180°

此题一出，大部分学生都用量角器量出各个角的度数，再计算。此时，教师追问：“虽然用量角器的方法可以算出它们的度数，谁能说说如果没有量角器该怎么办？”问题一出，学生就有多种方法，有的说可以把四边形沿对角剪成两个三角形，然后用180°×2即得四边形内角和是360°；有的通过画一画、剪一剪，连一连等方法算出答案。最后，师生得出结论：三角形可以由多边形裁剪得到。同样道理，几个三角形也能拼成多边形，说明三角形与多边形是有联系的，合理运用这种联系，会使以后学数学更轻松。这样的课尾使得整堂课更加精彩，更有数学味。

总之，在数学教学中，让学生通过教师的过渡性语言提取对所学知识探究中所积累的学习经验和方法，突显学习信息的生成，激发学生逐步深入思考，借助认知信息的作用和矛盾，恰当地应用过渡性语言，有效地促进学生的思维，从而让思维的正确方法清晰地显现在学习目标之中。

（作者单位：福建省莆田市荔城区麟峰小学）