基于相似日搜索的改进LMD与ESN相结合的短期电力负荷预测模型

张亚丽， 胡伯轩， 李莎莎， 罗 勇

(1.河南省电力勘测设计院 河南 郑州 450000； 2.郑州大学 电气工程学院河南 郑州 450001； 3.河南省工程咨询公司 河南 郑州 450000)

基于相似日搜索的改进LMD与ESN相结合的短期电力负荷预测模型

张亚丽1， 胡伯轩2,3， 李莎莎2， 罗 勇2

(1.河南省电力勘测设计院 河南 郑州 450000； 2.郑州大学 电气工程学院河南 郑州 450001； 3.河南省工程咨询公司 河南 郑州 450000)

短期电力负荷容易受到自然因素及社会因素的影响，这使得负荷预测比较困难.为了提高短期负荷的预测精度，提出了基于相似日搜索的改进局部均值分解(ILMD)和回声状态网络(ESN)相结合的短期电力负荷预测模型.首先用模糊聚类分析将与预测日最相似的多个日期筛选出来.然后把这些相似日的整点负荷数据按照时间先后排成一组数据序列，用改进的LMD进行分解，对分解出的各个分量分别建立一个ESN网络，对每一个网络分别训练并进行预测.最后把每个网络的预测结果累加起来就是最终的预测值.实验证明此方法能有效提高预测精度.

负荷预测； 局部均值分解； 回声状态网络； 相似日； 模糊聚类

0 引言

当前电能一般还不能大容量的存储，生产、输送和消费是在同一时间完成的.因此，电能的生产应每时每刻与电能的消费量保持平衡.精确预测电力负荷，既是为了保证人民生活和国民经济各部门对电力的需求，也是电力工业自身发展的需要[1-2].由于短期电力负荷容易受到自然因素和社会因素的影响，所以用传统的预测方法不能有效地提高负荷预测的精度.

目前常用的负荷预测方法主要有时间序列法[3]、回归分析法[4-5]、人工神经网络法[6-7]、小波-神经网络组合法[8]和模糊方法[9]等.电力负荷是一个非平稳的时间序列，为了能更精确地预测，将负荷先进行分解，分解出在不同频域，代表负荷不同变化特性的分量，根据每个分量特性再分别预测将会更加合理.小波分解是一种应用较为广泛的分解方法，文献[10]用小波分解的方法对短期电力负荷进行了预测，取得了比较好的效果.小波分解虽然很有效，但是分解时需要预先确定小波基，通常比较难选择，要根据经验来选择[11]，因此这个方法不能自适应地分解.为此研究者又将局部均值分解引入到预测中，将局部均值分解与神经网络结合起来进行电力负荷的预测也取得了很好的效果.在文献[12]中用的BP网络是一种局部搜索的优化方法，算法容易陷入局部极值，并且其收敛速度也比较慢.另外其所用的LMD中的滑动平均在低频信号时误差较大[13].回声状态网络是一种新型的递归神经网络，有良好的非线性逼近能力[14].文献[15]用经验模式分解(EMD)与回声状态网络相结合的方法对短期电力负荷进行预测.但是EMD在分解时有时会出现模态混叠的现象[16].

以上这些方法都只是在分解与网络上进行了改进，也没有考虑到各种自然、社会和气象因素对电力负荷预测的影响[17].为此，本文提出了基于相似日搜索的改进局部均值分解(ILMD)和回声状态网络(ESN)相结合的预测模型.改进的 LMD可避免低频信号分解的误差，ESN可避免传统神经网络收敛速度慢，易陷入局部极值等问题，因此，本预测方案可明显提高预测精度，减少预测时间.

1 预测模型的总体结构

本文的预测模型分为3部分：模糊聚类、改进局部均值分解、回声状态网络.用模糊聚类来筛选出与预测日期最相似的多个日期，并将这些日期的整点负荷值按时间顺序组成负荷数据序列，成为理想样本.之后用改进局部均值分解把理想样本分解成n个PF(product function)分量，每一个PF分量被分为2部分：训练样本和测试样本.针对每一个PF分量分别建立一个ESN，并用训练样本对其进行训练，用训练好的ESN进行预测.最后将同一时刻的每一个PF分量的预测结果累加就得到了这一时刻的预测值.其结构图如图1所示.

1.1 模糊聚类分析

电力负荷容易受天气状况、日期类型等因素的影响[18]，并且其精确度越来越受到关注.因此如何选择有效的训练样本就成为一个很重要的提高预测精度的因素.本文采用模糊聚类的方法选出与待测日相似日期的负荷作为训练样本会更有针对性.聚类分析是一种多元分析方法，它是用数学方法定量地确定样本之间的亲疏关系，从而客观地把样本划分为不同的类型.模糊聚类能将电力负荷与各种影响因素综合起来考虑[19].

在这里我们将日期类型、最高温度、最低温度作为对电力需求量影响最大的因素[20]，可以作为模糊聚类的特征指标.聚类步骤如下.

1) 用数字描述样本的特征.假设被聚类的样本集为X={x1，x2，…,xn}.每一个样本都有p种特征,记为xi=(xi1，xi2，…，xip)；i=1，2，…,n.

2) 用相关系数法求得原始特征数据矩阵的模糊相似矩阵R，由于R不具备可传递性，因而R不一定是模糊等价矩阵.

3) 运用合成运算R=R·R求出R的模糊等价矩阵S=R.

4) 选取适当水平α(0≤α≤1),得到α水平上的聚类.

1.2 改进的局部均值分解(ILMD)

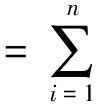
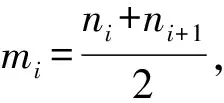
3) 从原始信号中分离出m11(t)，得到h11(t)，计算公式为：h11(t)=x(t)-m11(t).

4) 用上式得到的h11(t)除以a11(t)得到s11(t)，计算公式为：s11(t)=h11(t)/a11(t).

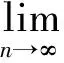
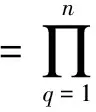
7) 第一个PF分量PF1就是纯调频信号s1n(t)和包络信号a1(t)的乘积，即PF1=a1(t)s1n(t).

8) 把PF1从原始信号x(t)中分离出来得到信号u1(t)，再对u1(t)重复以上过程，循环m次直到um(t)是一个单调函数，如：

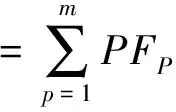
1.3 回声状态网络(ESN)

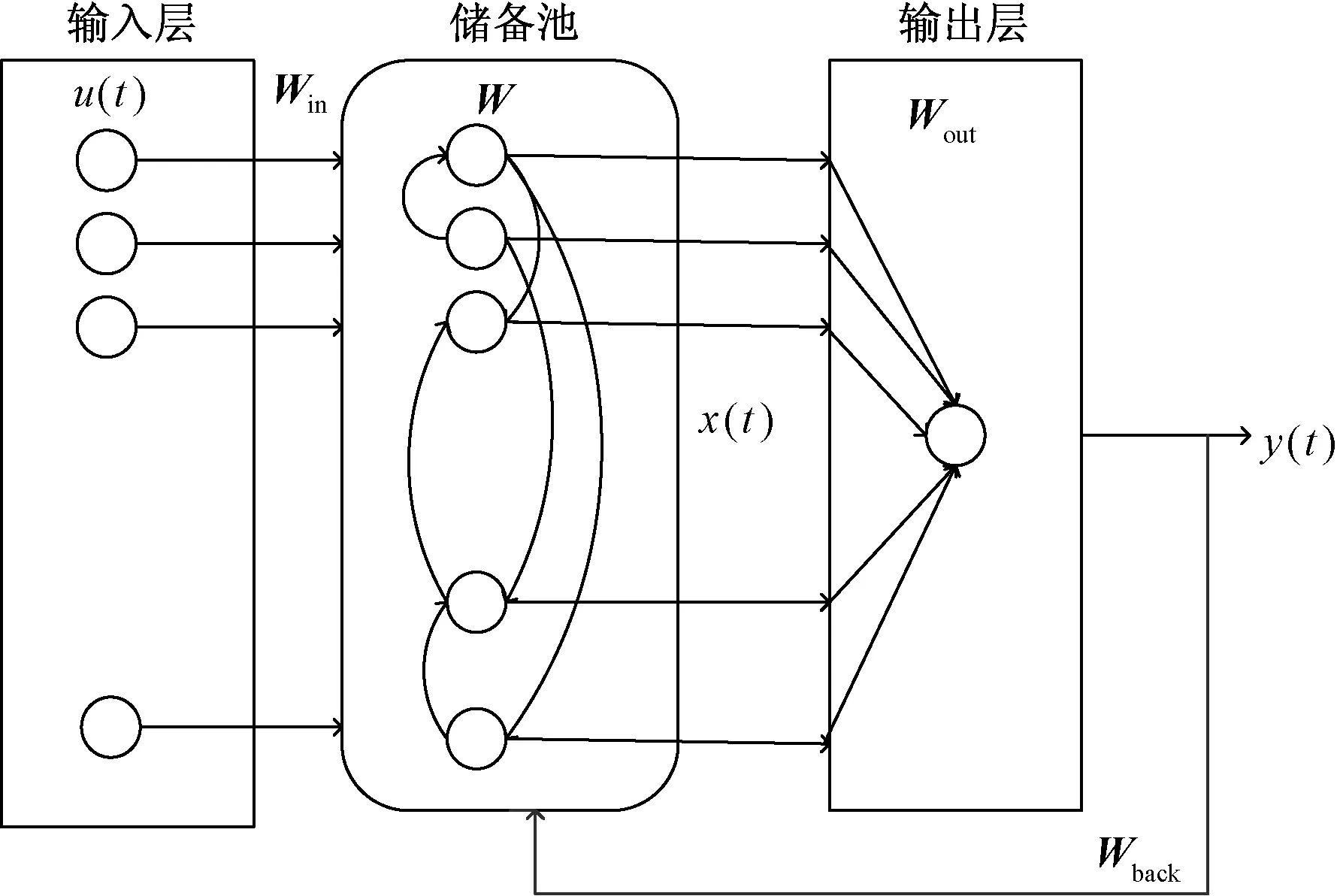
图2 ESN结构图Fig.2 Structure of ESN

ESN是一种新型的递归神经网络，是Jaeger等在2004年提出的[23].ESN引入了称作储备池的内部网络，ESN由3部分组成，分别是输入层、储备池、输出层.其核心结构是储备池，它是随机生成的大规模稀疏连接的递归结构.ESN结构图如图2所示.

假定在图2所示结构的输入层有K个节点，中间的储备池有N个节点，输出层有L个节点.

则在t时刻各层的状态为：

输入层的状态序列为u(t)={u1(t),u2(t),…,uK(t)}，

储备池的状态序列为x(t)={x1(t),x2(t),…,xN(t)}，

输出层的状态序列为y(t)={y1(t),y2(t),…,yL(t)}.

ESN的状态更新方程和输出方程分别表示为

x(t+1)=f(Winu(t+1)+Wx(t+1)+Wbacky(t)),

(1)

y(t+1)=fout(Wout(u(t+1),x(t+1),y(t)),

(2)

其中:Win、W、Wback分别是输入层到储备池、储备池内部之间的连接权值矩阵和输出层到储备池的反馈权值矩阵.W是一个稀疏连接矩阵，其稀疏度一般保持在1%～5%，并且其谱半径一般小于1.f(·)是储备池内部神经元之间的激活函数，一般取非线性函数以便使ESN具有非线性逼近能力，fout(·)是输出激活函数，一般是线性函数.Wout是储备池到输出层的连接权值矩阵.在ESN的训练过程中Win、W、Wback是建立网络时随机产生的.Wout是我们训练后得出来的.

2 实例分析

在这里我们用河南省某市2014年7月1日到8月25日所有的工作日的电力负荷为原始样本，用本文提出的基于相似日的ILMD和ESN相结合的模型来预测8月26日的电力负荷.具体过程如下所示.

第1步：相似日的选取.记录该市从2014年7月1日到8月26日所有工作日的气温情况(包括最高气温、最低气温两项)和星期类型.使之成为模糊聚类的特征指标，组成原始特征数据矩阵，利用模糊聚类方法的第2～3步，得出等价模糊矩阵.选择α值为0.962，就获得在α水平上的聚类，分类的仿真结果表明，和待预测日(8月26日)相似的有8天，分别是7月9日、7月16日、7月24日、7月30日、8月1日、8月19日、8月20日、8月22日.

第2步：ILMD分解.将第1步中得出的所有相似日的整点电力负荷数据(共216个时刻的数据)按时间先后顺序组成一个数据序列，并对该数据序列按照改进局部均值分解的方法进行分解，分解后由仿真结果最后得到4个分量和1个余量(用PF5表示)，如图3所示.8月22日与8月26日的分解主要是供后面的预测使用.

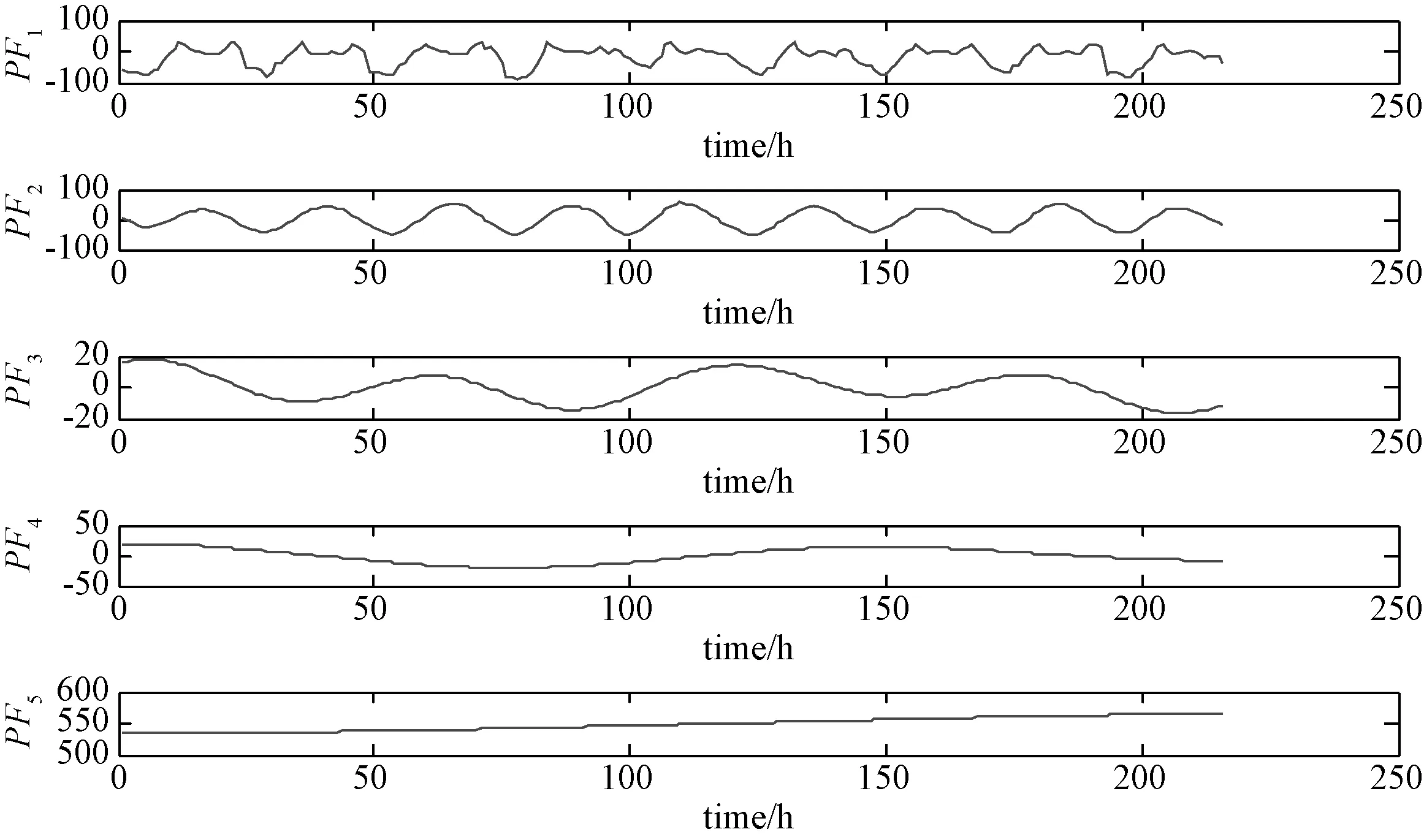
图3 ILMD分解结果图Fig.3 The decomposed results of ILMD

第3步：ESN网络训练.对于ESN网络，必须对其进行训练才能得到适合预测需要的网络.在这里对第2步中分解得到的4个分量和1个余量分别建立1个ESN网络，并分别对之进行训练.对于ESN1, 我们设定ESN1的输入层有12个节点，中间储备池是1 000个，输出层有1个节点.在训练时首先要初始化ESN1的参数Win、W和Wback，由设定可知，Win是一个1 000×12的矩阵，W是一个1 000×1 000的矩阵，Wback是一个1 000×1的矩阵，这3个矩阵是由Matlab随机产生的，状态向量x(0)初始化为0.其训练过程如图4.

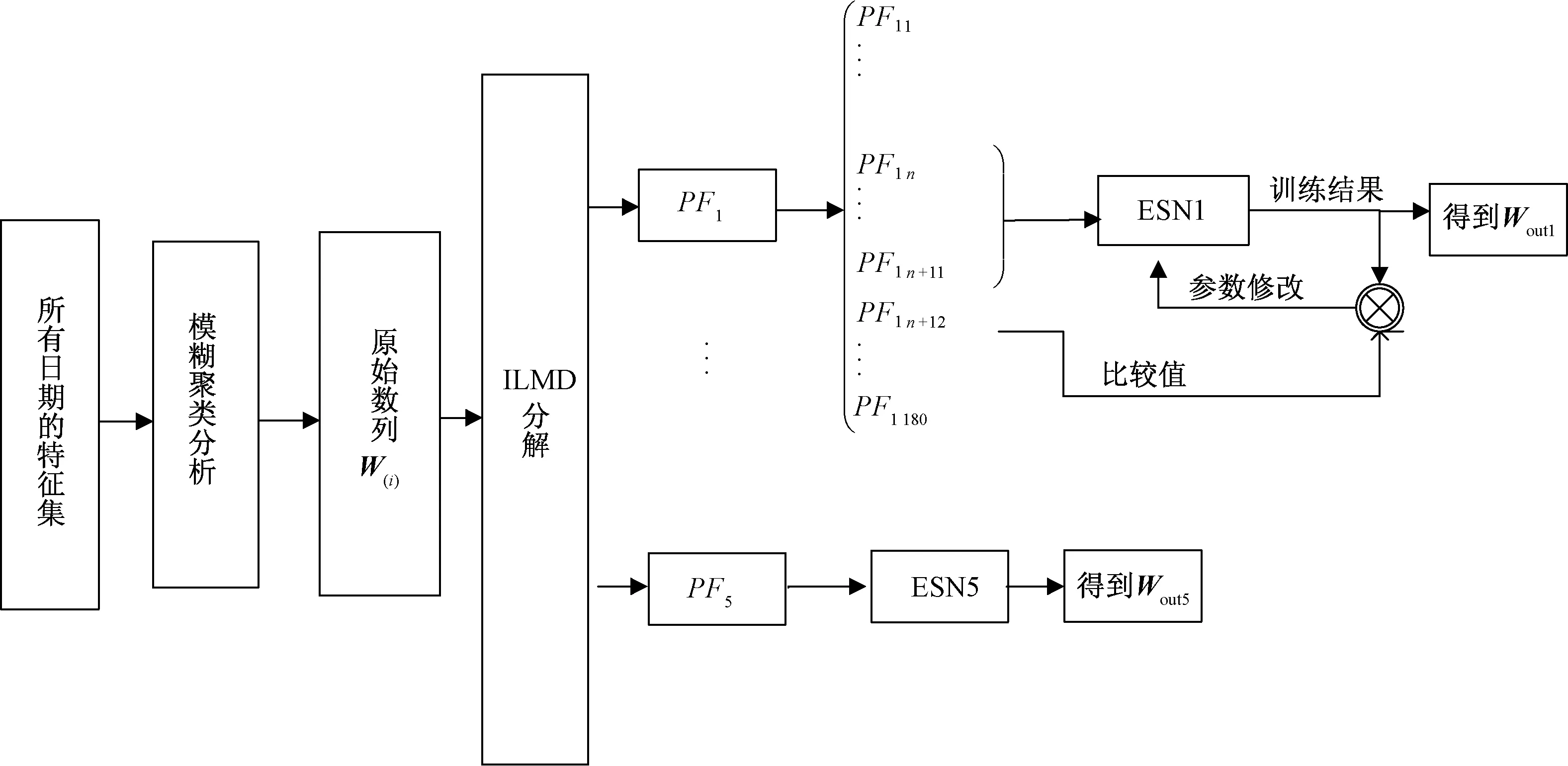
图4 训练过程图Fig.4 Training process of the method

选取第2步得到的相似日的整点负荷值的第1个分解量PF1的前180个数据作为训练样本.ESN网络的输入层是12个节点，因此可选择PF1n，PF1n+1，…，PF1n+11共12个时刻的数据作为网络输入，相应的PF1n+12作为ESN1网络的输出比较值，然后更新ESN1储备池状态向量，n取值为1,2，…，168，每组n对应了一组训练样本的输入与输出，通过改变n值，可实现输入与输出数据样本的滑动.ESN在初始训练时会受暂态效应的影响,其训练初始时会处于不稳定状态[11].最后确定一个抛弃时间点k0=20，舍弃之前的所有状态，取X=[x(k0)，x(k0+1),…，x(168)]T，Y=[y(k0)，y(k0+1),…，y(168)]T,Wout的训练可以用基本的线性回归算法求出：(Wout)T=X-1Y.对ESN1的训练就完成了.其他的ESN网络的训练与ESN1相同.

第4步：ESN网络预测.本文的预测过程如图5所示.第2步的ILMD分解的每个分量的后36个数据作为本文的测试集，如预测第i个分量第n个时刻的分解值时，对于ESNi，网络输入层输入的就是PFin-1，PFin-2，…，PFin-12这12个时刻的数据.比如要得到8月26日1点时负荷的PF1的值，就要用与8月26日最近的相似日(8月22日)的24点，23点,…,13点负荷的PF1值作为ESN1的输入，用训练得出的Wout来计算出预测的PF1值.

第5步：求取预测值.最后把所有的PF分量和余量的预测值累加起来，求取最终的预测值，计算公式为：

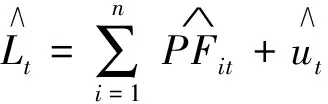
为了验证本文提出的预测模型的有效性，本文又用基于相似日搜索的ESN，基于相似日搜索的ILMD和BP相结合，以及ILMD和ESN相结合这3种预测方法来预测8月26日这天的负荷作为比较.对于基于相似日搜索的ESN预测模型，我们用的相似日期和ESN模型与本文相同，只是数据不经过ILMD分解直接进行预测；对于基于相似日搜索的ILMD和BP相结合的预测模型，样本和本文一样，只是最后用的BP网络，在这里选择BP的网络结构是12—20—1；对于ILMD和ESN相结合的预测模型，我们的样本用8月26日前8天的整点负荷数据,ESN网络与本文一样.仿真结果如图6所示.

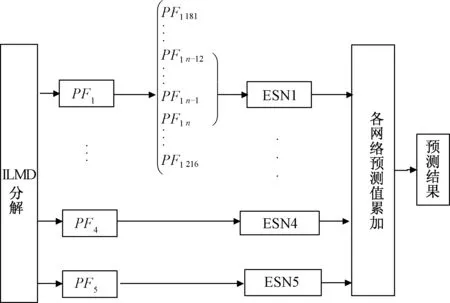
图5 预测过程图Fig.5 Forecasting process of the model

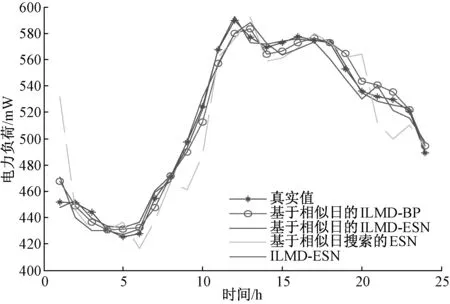
图6 预测结果对比图Fig.6 Comparison of forecasting results

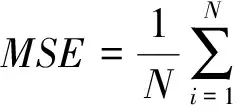
由表1～2可以看出，对于基于相似日搜索的ILMD-BP预测模型，由于此模型最后一部分用的是BP网络，它在训练过程中比较容易陷入局部极值点，而ESN的全局搜索比较好.对于ILMD-ESN预测模型，由于此模型只是用的预测日前几天的负荷数据训练网络，训练样本没有什么针对性，而本文的样本是与预测日特征相似日期的数据，因此会更有效.对于基于相似日搜索的ESN预测模型，这个模型直接将数据进行预测，不能使之呈现一定的规律，而本文则是将一定频域内的数据分解在一个分量上，使每一个分量都具有某种特征与规律，因此进行预测时会更精确.由以上分析可以看出，本文提出的预测模型其MAPE误差可低至0.6%左右，精度较其他方法有明显提升，因此，本文的预测模型效果比较理想.

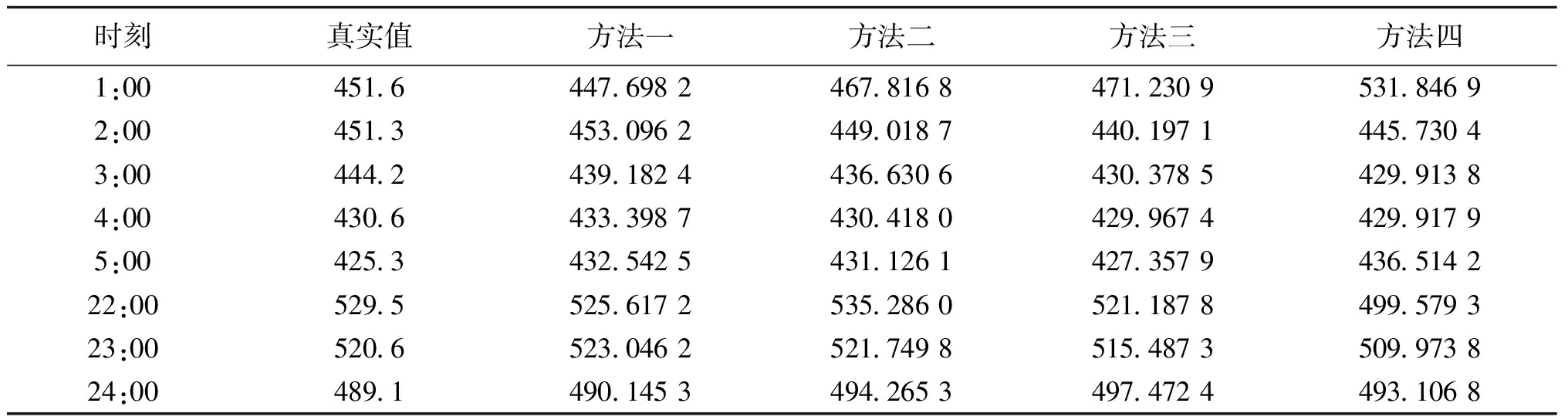
表1 负荷真实值与预测值

表2 预测方法指标值

3 结论

本文用基于相似日搜索的改进LMD与ESN相结合的预测模型对电力负荷进行预测.先用模糊聚类的方法选出所有的相似日，把相似日的负荷数据作为样本.再用LMD将这些样本分解成若干个PF和一个余量，之后对每一个PF和余量分别建立一个ESN网络，分别训练每一个ESN网络，并用训练好的ESN网络进行预测，最后把各个PF和余量的预测值累加就得到最后的预测值.仿真结果表明本文的预测模型预测效果比较理想，能有效提高预测精度.但本方案中基于LMD的时频分析方法易受采样效应的影响，同时其迭代终止条件如何确定，这些问题都是需要继续深入研究的.

[1] 张保会,尹项根.电力系统继电保护[M].北京：中国电力出版社,2009.

[2] 罗勇,李芳.基于负荷预测的电力市场寡头竞争分析[J].郑州大学学报(理学版),2013,45(3):110-114.

[3] SHI J, QU X L, ZENG S T. Short-term wind power generation forecasting: direct versus indirect ARIMA-based approaches[J]. Energies, 2011, 4(8): 1246-1257.

[4] 张伏生,王鸿.基于最小二乘回归分析的短期负荷预测[J].电网技术,2003,27(3):27-40.

[5] 吕效国,王金华,马阿芹,等. 自回归模型的自回归分析及其应用[J]. 扬州大学学报(自然科学版),2010,13(3):31-33.

[6] 王进,史其信. 神经网络模型在短期交通流预测领域应用综述[J]. 河南科技大学学报(自然科学版),2005,26(2):22-26.

[7] 牛东晓,王建军,李莉，等.基于粗糙集和决策树的自适应神经网络短期负荷预测方法[J].电力自动化设备,2009,29(10):30-34

[8] 祖哲,毕贵红,刘力，等.基于小波神经网络的电力系统短期负荷预测模型研究[J].计算机技术与发展,2012,22(10):237-241.

[9] 张平,潘学萍，薛文超.基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测[J].电力自动化设备,2012,32(11):121-126.

[10]刘梦良,刘晓华,高荣，等.基于相似日小波支持向量机的短期电力负荷预测[J].电工技术学报,2006,21(11):59-64.

[11]牛东晓,李媛媛,乞建勋，等.基于经验模式分解与因素影响的负荷分析方法[J].中国电机工程学报,2008,28(16):96-102.[12]兰花,常家宁,周凌，等. 基于局部均值分解与神经网络的短期电力负荷预测[J].电测与仪表,2012,49(5)：48-51.

[13]宋海军,黄传金,刘宏超，等.基于改进LMD的电能质量扰动检测新方法[J].中国电机工程学报,2014,34(10)：1700-1708.

[14]薛凯,周压建,平源，等.基于小波变换和ESN的P2P流量预测模型[J].计算机工程与设计,2012,34(4)：1147-1152.

[15]LUO Y, JIA X, CHEN S W. Short-term power load forecasting based on EMD and ESN[J].Advanced materials research, 2013,651:910-916.

[16]刘岱，庞松岭，骆伟,等.基于EEMD与动态神经网络的短期符合预测[J].东北电力大学学报,2009,29(6):20-26.

[17]栗然,刘宇,黎静华,等.基于改进决策树算法的日特征负荷预测研究[J].中国电机工程学报,2005,25(23):36-41.

[18]康重庆, 周安石, 王鹏,等.短期负荷预测中实时气象因素的影响分析及其处理策略[J].电网技术,2006,30(7):5-10.

[19]于龙.基于模糊聚类选取相似日的短期电力负荷预测[D].上海：上海交通大学,2013.

[20]罗勇, 郑金, 宁美凤，等.基于相似日搜索的PSO-WNN组合模型在短期电力负荷预测中的应用[J].信息与控制, 2013, 42(3):371-376.

[21]SMITH J S. The local mean decomposition and its application to EEG perception data [J].Journal of the royal society interface, 2005,2(5):443-454.

[22]杨德昌,唐巍,屈瑞谦，等.基于改进局部均值分解的低频震荡参数提取[J].中国电机工程学报,2013,33(4):135-141.

[23]JAEGER H，HASS H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication[J]. Science, 2004, 304(5667): 78-80.

(责任编辑：王浩毅)

The Short-term Power Load Forecasting Model of Combing ILMD and ESN Based on Similar Days Searching

ZHANG Yali1, HU Boxuan2,3, LI Shasha2, LUO Yong2

(1.HenanElectricPowerSurvey&DesignInstitute,Zhengzhou450000,China; 2.SchoolofElectricalEngineering,ZhengzhouUniversity,Zhengzhou450001,China; 3.HenanEngineeringConsultingCorporation,Zhengzhou450000,China)

Short-term power load was easily influenced by natural factors and social factors, which made load forecast more difficult. In order to improve the accuracy of short-term power load prediction, the forecasting mode of combing improved local mean decomposition (ILMD) and echo state network (ESN) based on similar days searching was proposed. Firstly, the days most similar to the forecasted date were selected by fuzzy cluster analysis. A data sequence was formed by uniting the similar days’ hourly loads together according to their time orders. Then, the ILMD was used to decompose the data sequence into several independent components, and an ESN was established for each component, separately. Each network was trained with similar daily load data. Using each trained network to predict the value of the corresponding component, the final result of prediction was the accumulation of all components predict values. Experiments showed that this method could effectively improve the prediction accuracy.

load forecasting； ILMD； ESN； similar days； fuzzy cluster analysis

2016-07-18

河南省青年骨干教师项目(2015GGJS-148);河南省产学研合作项目(152107000058)；河南省重点科技攻关项目(152102210036).

张亚丽(1984—)，女，河南商丘人,工程师，主要从事电力工程设计、电网规划研究，E-mail: 14872250@qq.com；通讯作者：罗勇(1977—)，男，湖南常德人，教授，主要从事数据预测、自动控制和最优决策研究，E-mail:luoyong@zzu.edu.cn.

TP18

A

1671-6841(2017)02-0120-07

10.13705/j.issn.1671-6841.2016189