细尾矿砂破坏准则的测试与安全影响*

林雪松，陈殿强 ，王来贵 ，赵　龙

(1. 辽宁工程技术大学 理学院，辽宁 阜新 123000; 2. 辽宁有色勘察研究院，辽宁 沈阳 110013 3 .辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

0　引 言

作为一种特殊的工业建筑物，尾矿坝安全问题一直备受关注，近年来，随着低品位矿石的大量开采和选矿工艺的不断提高，排入尾矿库的尾矿颗粒日益细化，给尾矿坝安全带来诸多挑战。众多学者围绕细尾矿砂构成的尾矿坝进行了研究。尹光志等[1-2]获得了加筋与不加筋尾矿坝的不同破坏模式并研究了细尾矿砂的渗流规律；乔兰等[3]分析了细颗粒含量对尾矿工程性质的影响；余新洲[4]设计了一种三维立体式排渗系统并验证了系统的合理有效性；李巧燕等[5]对固结不同时间的小尺寸尾矿坝筑坝模袋进行了摩擦和受压性能的试验研究；巫尚蔚等[6]建立了细粒尾矿粒径分布的Weibull函数模型。

破坏准则是尾矿坝安全评估的重要基础，与细尾矿砂破坏准则相关的研究有：李世海等[7]提出了一种基于剪应变强度分布的新强度准则；罗强等[8]探讨了将Barton-Bandis破坏准则参数转化为线性Mohr-Coulomb破坏准则抗剪强度参数的2种常用方法。路德春等[9]探讨了广义非线性强度理论与Mohr-Coulomb、Drucker-Prager 准则的变换关系；邵龙潭等[10]通过研究发现土的本构关系模型研究应该包括土体未发生破坏时的应力应变关系、破坏准则和破坏后沿剪切带的摩擦滑动性质；宋新江等[11]获得了水泥土的广义Tresca准则和广义Mises准则模型参数。郭建强等[12]对岩石屈服与破坏准则进行了研究；韩龙强等[13]开展了基于Hoek-Brown破坏准则的强度折减法研究；费建波等[14]分析了由Drucker-Prager和Mohr-Coulomb准则所得到的材料强度参数；彭瑞等[15]针对Hoek-Brown强度准则的较复杂地质参数，提出利用Mohr-Coulomb强度准则参数替代。

纵观以往的研究，前人针对细尾矿砂构成的尾矿坝在组成特性、渗流过程、溃决模式和加固方法方面取得了巨大进展，但研究内容不包括细尾矿砂的破坏准则；前人研究了岩土材料破坏准则的种类、不同破坏准则间的关系，但未发现针对尾矿砂破坏准则的专门研究，实际中需要尾矿砂破坏准则时，都是套用岩石或砂土的破坏准则，由于细观结构和组构成分的特殊性，还有放矿与沉积过程中复杂的固-液-气-化(学)耦合作用[16]，细尾矿砂的物理力学性质具有独特特点，需单独进行研究。

笔者在前人研究的基础上，拟通过HCA实现静水压力、Lode角不变，逐步增加广义剪应力直至试件破坏的应力路径，以此获得细尾矿砂的破坏准则，并将破坏准则引入数值计算模型研究破坏准则的选取、分布与尾矿坝安全状态的关系，以期为实际尾矿坝安全状态分析提供基础材料。

1　试验设计与方案

1.1　试验对象

以某铁尾矿砂为试验对象进行研究，颗粒组成如表1所示，从表1中可看出，小于0.019 mm粒径含量大于50%，大于0.074 mm粒径含量小于10%，大于0.037 mm粒径含量小于30%，因此试验对象完全可以归类为细尾矿砂[17-18]。通过击实控制干密度为1.76 g/cm3。

表1　细粒尾矿砂粒径组成Table 1　The ingredients of fine tailings　%

1.2　试验内容

试验以探索细尾矿砂破坏准则形式、特点为核心目的。破坏准则采用主应力空间的破坏曲面来展示，曲面可分别用子午平面和π平面的破坏曲线来表示，为得到破坏曲线需使试件先在恒定静水压力下完成反压饱和与恒压固结，然后从固结应力状态开始，在保持静水压力和Lode角不变的前提下，逐渐增加广义剪应力数值，直至试件破坏，从而获得试验对象的破坏应力点。如此设置应力路径是为使试件沿主应力空间中的直线由初始应力点达到破坏应力点，作为两点间的最短距离，直线应力路径可减少试验中间状态、节省试验资源。初始固结压力取值分别为100，200，300，400 kPa，每种固结压力下Lode角分别取-π/6，-π/12，0，π/12，π/6，共计可得20个破坏应力点，由于Lode角以π/3为周期，因此作出1个周期的图形之后其他部分的图形可直接复制得到。

1.3　试验仪器与试件

以英国GDS公司的空心圆柱扭剪仪(Hollow Cylinder Apparatus，HCA)为核心仪器进行试验，仪器主体部分为主机、控制器和DTI控制盒。为保证制样和装样过程得以顺利进行，并尽量减小制样扰动，制作了制样底座、击实仪和装样支架用以配合HCA试验，试验所需主要设备如图1所示。HCA使用空心圆柱试件，试件内半径ri=3×10-2m，外半径ro=5×10-2m，高H=0.2 m。试件整体和任意单元的受力分别如图2所示。图中po表示外围压， kPa；pi表示内围压， kPa；W表示轴向荷载，kN；MT表示扭矩，N·m；σz表示轴向应力， kPa；σr表示径向应力， kPa；σθ表示转角向应力， kPa；τzθ表示剪应力， kPa。HCA的输入参数是po，pi，W和MT，可输出σz，σr，σθ和τzθ，4个应力的计算式为：

(1)

仪器可测参量还包括：

(2)

式(2)中σ1表示大主应力， kPa；σ2表示中主应力，

kPa；σ3表示小主应力， kPa；p表示静水压力， kPa；q表示最大剪应力， kPa；b表示中主应力比；qJ表示广义剪应力， kPa。

图1　试验仪器Fig. 1　Testing Apparatus

1.4　应力路径的实现

通过改变输入参量值可获得所需应力路径，在MT=0前提下，由(1)～(2)推得各参量变化量如式(3)所示，θσ表示Lode角。由式(3)可根据需要的θσ和qJ控制ΔW，Δpo和Δpi的量值。初始固结状态要求po=pi=p*,W=0，因此有W=ΔW，内外围压的值分别为po=p*+Δpo和pi=p*+Δpi。p*为初始固结应力。

(3)

2　试验结果与分析

2.1　子午平面的破坏曲线

子午平面破坏曲线如图3所示。

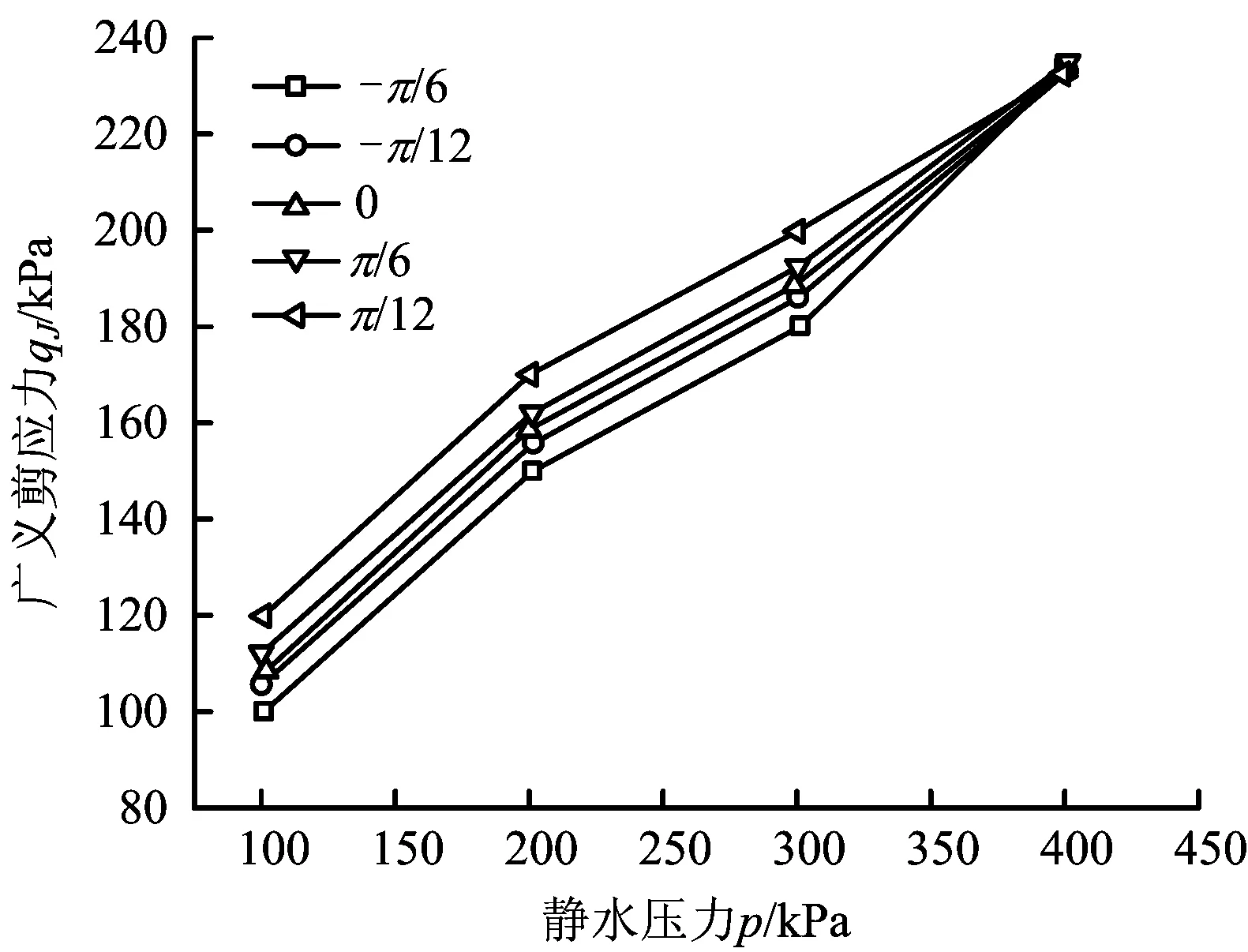
图3　子午平面破坏曲线Fig.3　Failure curve of meridian plane

分析图3可知，尽管数值大小有差别，但各曲线变化趋势基本相同，均为单调递增，广义剪应力与静水压力具有明显的线性关系。分析原因为：尾矿砂的抗剪强度源于颗粒间相互作用的摩擦力，静水压力提供了颗粒间的正压力，随着静水压力的增大，正压力增大，进而摩擦力增大，因此抗剪强度增加，在曲线上表现出来的特征是破坏应力点的广义剪应力随静水压力的增加而增加。总体来说曲线体现了细尾矿砂的摩擦材料特性，且因曲线斜率基本不变，可断定在试验应力范围内，内摩擦角不随静水压力的变化而变化。

2.2　π平面的破坏曲线

π平面上的破坏曲线如图4所示。

图4　π平面破坏曲线Fig. 4　Failure curve of π-plane

分析图4可知，在p值较小的状态，曲线形状与Mohr-Coulomb准则比较相似，但随着p值的增加，曲线形状逐渐变成圆形，与Drucker-Prager准则一致。圆形破坏曲线体现的特点是与θσ无关，曲线由不规则图形逐渐变成圆形说明在p值较小的状态，尾矿颗粒之间的结合并不紧密，破坏曲线的形状与θσ有关，但随着p值的增大，试件在静水压力作用下内部颗粒之间逐渐紧密接触。呈现出新的破坏特性：与θσ无关。Mohr-Coulomb准则与中主应力无关，而Drucker-Prager准则与中主应力有关，因此试验结果说明对细尾矿砂来说，中主应力的影响与静水压力相联系，在静水压力较小的状态，中主应力对破坏准则基本没有影响，但是随着静水压力的增加，中主应力的作用开始变得明显，需要被考虑进来。在实际尾矿工程中，如果分析的问题静水压力较小，可取为Mohr-Coulomb破坏准则，若面临的问题静水压力较大，应考虑取为Drucker-Prager准则。目前尾矿工程中通常都将尾矿材料的破坏准则取为Mohr-Coulomb准则，只能说与试验结果部分符合，最佳分析方法是浅层尾矿砂静水压力较小，采用Mohr-Coulomb准则，深层尾矿砂静水压力较大，采用Drucker-Prager准则，从图4中可看出，p为100 kPa时图线与Mohr-Coulomb准则非常相似，但从p为200 kPa开始Lode角造成的影响在数值上已经很不明显，因此可将破坏准则的分界线取为200 kPa。

3　基于试验结果的坝体安全状况计算与分析

3.1　计算模型

通过FLAC3D5.0软件建立数值模型进行计算与对比分析。模型长120 m，最大高度45 m。模型的物理力学参数如表2。其中尾矿砂的内摩擦角取了3个值，以此来得到后面分析所需的不同初始安全状态。模型左右边设置为水平向约束，底边与初期坝设置为水平和竖直向约束。分别建立仅设置Mohr-Coulomb准则的单准则模型和根据静水压力值分别设置Mohr-Coulomb准则与Drucker-Prager准则的双准则模型。对于单准则模型，可直接设置破坏准则并利用solve fos命令计算安全系数。对于双准则模型，则需先利用FISH语言编制程序设置每个单元的破坏准则，然后根据程序是否收敛来计算安全系数，根据试验结果以静水压力200 kPa为破坏准则的分界点，将静水压力大于等于200 kPa的单元设置为Drucker-Prager准则，其余单元设置为Mohr-Coulomb准则，双准则模型中不同准则单元分布如图5所示。

表2　物理力学参数Table 2　Physical mechanics parameters

图5　模型单元结构Fig. 5　Element structure of model

3.2　计算结果与分析

图6　Mohr-Coulomb准则滑面Fig. 6　Slip surface of Mohr-Coulomb criterion

图7　双重准则滑面Fig.7　Slip surface of double criteria

单准则模型计算坝体安全系数为0.895，得到滑面如图6所示。双准则模型计算安全系数为0.971，得到滑面如图7所示。首先，从安全系数数值来看，2种情况下坝体安全状态差别很明显；然后，从滑面图的比较中可以看出，滑面的形状与分布区域出现了明显的变化，且双准则模型中的最大剪应变数值整体水平明显大于单准则模型，由此可断定破坏准则的变化对坝体安全状态分析结果产生了明显的影响。为进一步研究破坏准则的分布对坝体安全度的影响，在3种不同初始安全状态下，均由模型底部开始逐渐增加Drucker-Prager准则单元总数，得到安全系数的变化曲线如图8所示。3种不同的初始安全状态指的是在单独Mohr-Coulomb准则下安全系数值分别为0.551，0.900和1.250。分析图8可知，在不同初始安全系数下，安全系数的变化趋势完全相同，当Drucker-Prager准则单元比重较小时，坝体安全系数并没有明显的变化，但Drucker-Prager准则单元比重达到31.33%时安全系数开始随着比重的增加迅速变化，达到60.67%以后，安全系数又出现了基本不变的状态。但不同初始安全系数下安全系数的变化幅度是不同的，随着初始安全系数的增加，安全系数的变化幅度单调递增。原因可归结为：Drucker-Prager准则单元数是从模型底部向上增加的，在单元比重增加的开始，Drucker-Prager准则单元并未进入滑面区，当单元比重达到31.33%左右，才开始进入滑面区，因此会对安全系数产生影响，当单元比重达到60.67%左右，滑面区内Drucker-Prager准则单元数量已达到最大值，接下来不会再增加，因此继续增加Drucker-Prager准则单元比重不会对安全系数产生影响，由此可知，Drucker-Prager准则单元比重对坝体安全系数的影响主要源于滑面区内单元的数量。此外随着Drucker-Prager准则单元比重的增加安全系数逐渐增加，最大剪应变也增加，原因是计算中Drucker-Prager准则使用的是Mohr-Coulomb准则的外角外接圆，因此由Mohr-Coulomb到Drucker-Prager准则变化中，破坏曲面在π平面内的面积增大，意味着破坏时需要的应力更大，因此不容易破坏，安全系数增大，但是在达到较大应力破坏时也会形成较大的变形，因此最大剪应变增加。

图8　安全系数的变化Fig. 8　Change of safety factor

4　结论

1)细尾矿砂破坏准则在子午平面曲线特点为：破坏广义剪应力随静水压力的增加单调递增，变化率基本恒定。在π平面曲线特点为：静水压力较小状态与Mohr-Coulomb准则一致，与Lode角有关，与中主应力无关，静水压力较大状态与Drucker-Prager准则一致，Lode角无关，与中主应力有关，针对试验用细尾矿砂，2种情况静水压力分界点可初步选在200 kPa。

2)数值计算结果表明：尾矿坝安全状态评判结果与破坏准则选取有直接关系，利用Mohr-Coulomb准则计算的安全系数小于Drucker-Prager准则。若坝体内部同时存在2种破坏准则，安全系数介于单独使用1种准则计算的安全系数之间，随着Drucker-Prager准则单元所占比重的增加，坝体安全系数具有增加的趋势，但增加状况与滑面区内Drucker-Prager准则单元数量有关，数量变化则安全系数变化，数量不变则安全系数变化不明显。

[1]尹光志,魏作安,万玲,等.细粒尾矿堆坝加筋加固模型试验研究[J].岩石力学与工程学报,2005,24(6):1030-1034.

YIN Guangzhi, WEI Zuoan, WAN Ling, et al. Test study on stability of fine grained tailings dam in geogrid reinforcement situation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 1030-1034.

[2]尹光志,敬晓飞,魏作安,等.粗、细尾砂筑坝渗流特性模型试验及现场实测研究[J].岩石力学与工程学报,2010,29(S2):1030-1034.

YIN Guangzhi, JING Xiaofei, WEI Zuoan, et al. Study of model test of seepage characteristics and field measurement of coarse and fine tailings dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3710-3718.

[3]乔兰,屈春来,崔明.细粒含量对尾矿工程性质影响分析[J].岩土力学,2015,36(4):923-945.

QIAO Lan, QU Chunlai, CUI Ming. Effect of fines content on engineering characteristics of tailings[J]. Rock and Soil Mechanics, 2015, 36(4): 923-945.

[4]余新洲.一种三维立体排渗方式在细粒级尾砂筑坝中的应用[J].岩土工程学报,2016,38(S1):74-78.

YU Xinzhou. Application of 3D solid water seepage method in construction of fine fraction tailings dam[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(S1): 74-78.

[5]李巧燕,王惠栋,马国伟,等.尾矿坝筑坝模袋力学性能试验研究[J].岩土力学,2016,37(4):957-964.

LI Qiaoyan, WANG Huidong, MA Guowei, et al. An experimental study of the mechanical performance of tailings dam geofabriform[J]. Rock and Soil Mechanics, 2016, 37(4): 957-964.

[6]巫尚蔚,杨春和,张超,等. 基于Weibull模型的细粒尾矿粒径分布[J].重庆大学学报,2016,39(3):1-12.

WU Shangwei, YANG Chunhe, ZHANG Chao, et al. Particle size distribution of fine-grained tailings based on Weibull distribution[J]. Journal of Chongqing University, 2016, 39(3): 1-12.

[7]李世海,周东.地质体渐进破坏面的计算模型与剪切面破坏准则[J].岩石力学与工程学报,2013,32(S2):3009-3015.

LI Shihai, ZHOU Dong. Computational model of progressive failure plane in geological body and failure criterion of shear plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3009-3015.

[8]罗强,赵炼恒,李亮,等. 基于Barton-Bandis准则的锚固边坡稳定性分析[J].岩土力学,2013,34(5):1351-1359.

LUO Qiang, ZHAO Lianheng, LI Liang, et al. Stability analysis of anchored rock slope based on Barton-Bandis failure criterion[J]. Rock and Soil Mechanics, 2016, 2013, 34(5): 1351-1359.

[9]路德春,杜修力. 岩石材料的非线性强度与破坏准则研究[J].岩石力学与工程学报,2013,32(12):2394-2408.

LU Dechun, DU Xiuli. Research on nonlinear strength and failure criterion of rock material [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(12): 2394-2408.

[10]邵龙潭,刘港,郭晓霞.三轴试样破坏后应变局部化影响的实验研究[J].岩土工程学报,2016,38(3):385-394.

SHAO Longtan, LIU Gang, GUO Xiaoxia. Effects of strain localization of triaxial samples in post-failure state [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 385-394.

[11]宋新江,徐海波,周文渊,等.水泥土应力-应变特性真三轴试验研究[J].岩土力学,2016,37(9):2489-2495.

SONG Xinjiang, XU Haibo, ZHOU Wenyuan, et al. True triaxial test on stress-strain characteristics of cement-soil[J]. Rock and Soil Mechanics, 2016, 37(9): 2489-2495.

[12]郭建强,刘新荣,王军保,等.基于弹性应变能的岩石强度准则[J].岩土力学,2016,37(S2):129-136.

GUO Jianqiang, LIU Xinrong, WANG Junbao, et al. Strength criterion of rock based on elastic strain energy[J]. Rock and Soil Mechanics, 2016, 37(S2): 129-136.

[13]韩龙强,吴顺川,李志鹏. 基于Hoek-Brown准则的非等比强度折减方法[J].岩土力学,2016,37(S2):691-696.

HAN Longqiang, WU Shunchuan, LI Zhipeng. Study of non-proportional strength reduction method based on Hoek-Brown failure criterion[J]. Rock and Soil Mechanics, 2016, 37(S2): 691- 696.

[14]费建波,介玉新,张丙印,等.土的三维破坏准则在颗粒流模型中的应用[J].岩土力学,2016,37(6):1809-1817.

FEI Jianbo, JIE Yuxin, ZHANG Bingyin, et al. Application of a three-dimensional yield criterion to granular flow modeling[J]. Rock and Soil Mechanics, 2016, 37(6): 1809-1817.

[15]彭瑞,赵光明,孟祥瑞. 岩体强度参数新解及应用[J].中国安全生产科学技术,2014,10(5):43-48.

PENG Rui, ZHAO Guangming, MENG Xiangrui. Latest explanation of rock mass strength parameters and its application [J]. Journal of Safety Science and Technology, 2014, 10(5): 43-48.

[16]陈生水. 尾矿库安全评价存在的问题与对策[J]. 岩土工程学报,2016,38(10):1869-1873.

CHEN Shengshui. Problems and countermeasures of safety evaluation of tailing pond[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(10): 1869-1873.

[17]《中国有色金属尾矿库概论》编辑委员会.中国有色金属尾矿库概论[R].北京:中国有色金属工业总公司,1992.

[18]尾矿设施设计参考资料编写组.尾矿设施设计参考资料[M].北京:冶金工业出版社, 1980.