MEMS加速度计二阶非线性补偿方法研究*
2017-04-14王一焕刘一鸣李文豪
王一焕,李 杰,刘一鸣,兰 洋,李文豪
(中北大学电子测试技术重点实验室,太原 030051)
MEMS加速度计二阶非线性补偿方法研究*
王一焕,李 杰*,刘一鸣,兰 洋,李文豪
(中北大学电子测试技术重点实验室,太原 030051)
微惯性集成测量组合(MIMU)中的惯性传感器,陀螺仪和加速度计的标定补偿研究大多集中在安装误差角补偿和一阶线性常数的计算上,对二阶非线性系数的测量、计算研究的不多不深。通过分析含二次非线性系数的加速度计输出模型,提出一种补偿二次非线性系数的方法,并进行了完善的理论分析和试验。最终通过计算能有效补偿MIMU的输出精度,为后续的导航信息解算奠定了基础,具有重要的工程应用价值。
MIMU;标定;二阶非线性系数;误差补偿;
某型高速旋转弹在飞行过程中,轴向旋转角速率极大,角加速度变化极为剧烈。实现高精度的姿态测量对于弹体的精确打击具有重要的意义。MEMS惯性系统不向外辐射信息,自主性好,抗过载能力强,是旋转弹姿态测量的不二之选。
MIMU是惯性导航的核心,是由加速度计和陀螺仪六维惯性测量组合器件。其中角加速度计用于敏感载体三轴的比力,用于更新载体速度和位置,显然惯性传感器的输出精度直接决定了导航解算的精度。即便通过标定一阶线性标度因数,补偿安装误差角来提高MIMU中三轴加速度计的精度,其输出与理论值比较,依然存在1 mgn~3 mgn的误差。本文对加速度计输出中的二阶非线性系数误差进行了详细的理论分析,并提出了补偿方案,及数据处理方案,解决了安装误差角对非线性系数计算的不利影响。计算表明,补偿二阶非线性系数能在标定的基础上再次提高三轴加速度计的输出精度。
1 加速度计输出模型
1.1 含二阶非线性系数的加速度计输出模型
加速度计敏感载体某轴向上的比力并输出相应的电压。查阅国军标《JJF 1427-2013微机电(MEMS)线加速度计校准规范》[1]中的加速度计静态模型方程,并忽略通过标定可以补偿的各个耦合项系数可得:
(1)
三轴加速度计组合因为安装误差角、失准角的存在,传感器坐标系(a系)是一个斜坐标系和载体坐标系(b系)并不重合,通常假定两坐标系原点重合。如图1所示,加速度计的实际位置,如X轴加速度计实际位置与b系三轴都存在夹角。
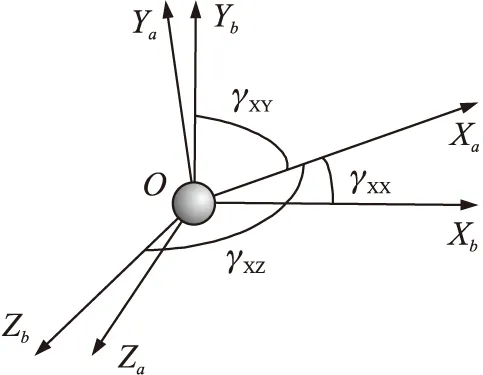
图1 坐标系定义
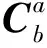
(2)
综合式(1)和式(2)写出包含二次非线性系数的三轴加速度计的输出模型。
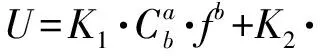
(3)
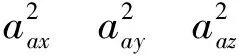
经过转台标定可以得到标度因数矩阵K,且存在如下关系[3]:
(4)
将式(4)代入式(3)并变形可得:
fb=K-1·(U-U0)-K-1·K2·(fa)(2)
(5)
上式说明了,电压与最终转换得到的b系比力之间的关系。同时根据标度因数矩阵和安装误差角矩阵之间的转化关系,单轴标度因数用下式计算:
式(4)中,同时存在b系和a系比力。要求解fb,需要先求fa,但在标定过程中fa是未知的,所以无法通过直接对式(5)进行函数拟合得到各项参数。
1.2 加速度计输出特性分析
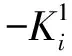
同时二次方程总能解出两个根,但一个电压输出必然只能对应一个敏感到的比力值。容易证明方程一定有两个实数根(因为Δ>0)。根据二次方程求根公式求出两根,并解出其二次项趋于零时的极限:
(6)
将式(6)与不计二次项时的比力作对比,显然应该取a+为二次方程的根。
试验表明MEMS加速度计的分辨率一般不超过0.1 mgn[4-5]。由于计算误差,或者更高次项的影响,二次项矩阵K2不是严格的对角矩阵,但是非对角线上的元素非常小,计算过程中完全可以忽略不计。
2 非线性系数的标定补偿法
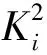
2.1 加速度计标定试验误差建模
本文在进行加速度计标定时,选取各个轴向分别在与水平面夹角为θ1、θ2、θ3…等多个位置上静置30 s(本文采用15°、30°、45°…360°等25个位置上静置30 s),并进行数据采集。每个静置角度上所测得的电压值取平均值作为静置于该角度下的加速度计输出。通过输出电压与静置角度之间的函数拟合可以算出标度因数矩阵K和三轴的电压零点。标定过程如图2所示。图2中箭头方向代表待标定的加速度计的方向,重量方向竖直向下。

图2 加速度计标定示意图
由式(3)可知,二次非线性系数组成的矩阵K2为对角阵,所以下面只分析K2对角线上的元素,假定标定过程中j轴加速度计静置角度为θ时,忽略二阶非线性系数;i轴向上的加速度计的输出为[7-8]:
Uij=Kij·sinθ+Cij·cosθ+Ui0
(7)
其中余弦项是安装误差角造成的,其系数也是标度因数矩阵中与Kij同行不同列的元素(或为其相反数),根据标定试验流程的不同Cij的取值也会有不同。根据数学理论可知[9],重力分量sinθ与电压之间的关系为平面上一斜椭圆,且椭圆中心位于(0,Ui0)上。不计高次分量时,进行以式(7)为函数关系的θ与Uij的非线性拟合就可以得到标度因数矩阵和电压零点(下文中称为一次拟合)。
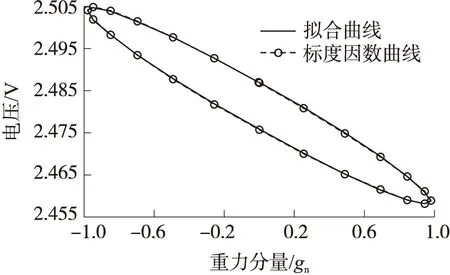
图3 标度因数曲线
图3是标定Y轴加速度计时,X轴加速度计的输出电压值画出的标度因数曲线,横坐标为重力分量,纵坐标为电压,虚线是进行了一次拟合后的理论曲线。
根据式(6)和式(7)联立可以得到不计非线性系数时计算出的a系比力:

(8)
若计入二阶非线性常数的影响,那么该轴上的比力将变得非常复杂。试验表明用式(8)代替a系中的比力时,误差可以忽略不计,在非线性系数非常小的情况下,可以忽略不计。所以以上式代替a系中的比力是在误差允许范围内的。代入式(6)得:
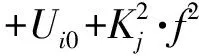
(9)
式(8)总可以利用辅助角公式整理成如下形式:
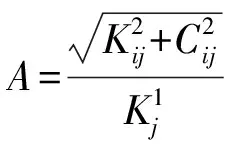
其中φ是初相位,容易证明初相位是一个很小的角度,并不影响后续的计算过程。振幅A表征了安装误差角对二次非线性系数测量的影响,可以通过测得的标度因数矩阵计算。虽然i,j所表示的轴向不同,会造成A的取值也有所不同,但A的值一般约等于0或1。进而式(9)可变形为:
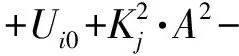
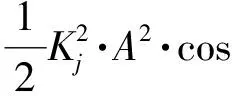
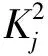
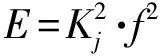
(10)
式(10)表明,忽略二次项进行一次拟合之后得到的误差是一条周期为π的余弦曲线。同时振幅A可以通过标度因数矩阵计算得到,所以计算出的二次项不受安装误差角的影响,计算重复性好。
2.2 非线性系数的拟合计算
为验证二次项系数补偿计算的重复性,对同一MIMU中的X轴加速度计进行两次相同的标定试验。试验1完成后又重新拆卸并安装了MIMU,再次进行了试验2,两次试验的安装矩阵一定存在差别。分别对两次试验的加速度计输出进行一次拟合后得出的拟合误差如图4所示。
显然两次试验却拟合出了相同的误差图像,并且误差曲线形状与理论分析得形状一致。对一次拟合误差再次进行非线性拟合,拟合的函数形式为式(8),图5为拟合结果。
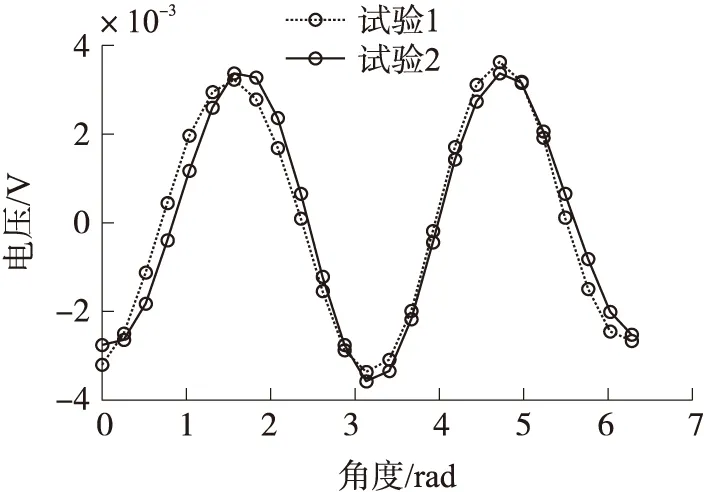
图4 标度因数曲线拟合误差
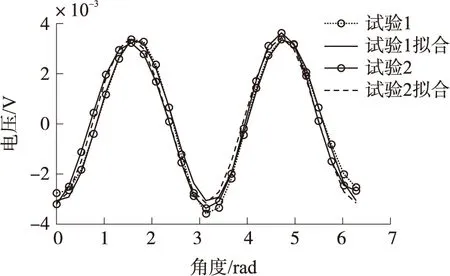
图5 二次拟合误差
将上述拟合称为二次拟合,拟合得出的系数如表1所示。
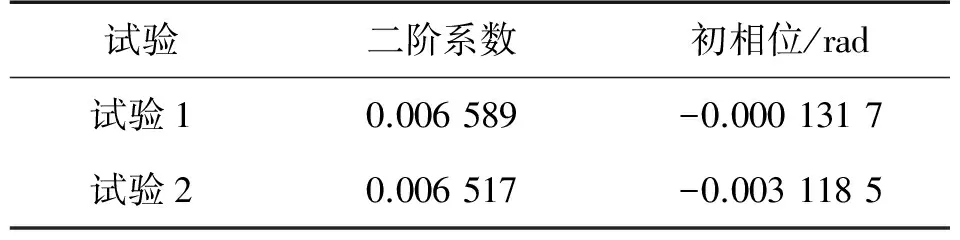
表1 试验1、试验2二次拟合结果
两次试验的拟合结果非常接近,误差数量级仅在10-5V,高于加速度计分辨率,说明利用标定试验数据的一次拟合误差能有效计算出二阶非线性系数,且重复性较好,基本去除了安装误差对二阶非线性系数计算的影响。对理论分析做出了有力的验证。
2.3 非线性系数的迭代补偿
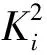
事实上在标定过程中,不明确标度因数矩阵和零点电压的情况下,fa始终无法通过理论分析计算出精确的值,所以无法通过直接法一次性地求出K矩阵和零点等参数,故本文采用迭代法减小误差[10]。
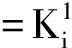
m=0,1,2,…
对于某一轴向上的加速度计而言,存在迭代方程组:
Ui(m)=H(m)·X(m+1)
(11)
式中:m是迭代次数,Ui是加速度计某轴向上输出电压组成的矩阵,X是需要拟合的系数,H是转台静置在各个角度时的所有轴向的比力及计算得出的a系比力构成的矩阵:
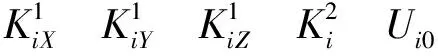
矩阵H中不确定的数仅为第4列,其他列均为固定常数。在第m-1次迭代过程中,首先解出矩阵X的值,尔后利用这些参数与式(27)求出fa(m),即矩阵H的第4列,相当于求出了矩阵H(m),求解式(28)便求出了X(m)。利用X(m)又能求出H(m+1)进行第m+1次迭代。为保证计算精度的同时缩短计算时间,本文迭代选择5次。
在每一次循环之内都需要求解形如式(28)的方程,所以有必要讨论该方程的求解方法。显然该方程为一个线性超静定方程组,未知数个数小于方程组个数,通过多次试验得知,该方程通常不存在唯一解,只能求出最优解。本文采用最小二乘法,最优化估计指标为偏差的平方和最小[12],如下式所示,理论上这样的最小二乘解有且仅有一个。
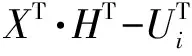
本文利用MATLAB中的lsqcurvefit函数进行最小二乘法解的计算,即矩阵X的计算。
2.4 标定试验结果
通过由3个量程均为±2gn的model 1221L系列加速度计集成的MIMU,借助GDL3-WD-ZB三轴位置速率摇摆温控转台对MIMU进行转台标定试验。采集电路采样频率为5 kHz。标定完成后,加速度计输出与理论输出之间不可避免的仍然会存在一定的误差,通过比较同一个加速度计在经过一次拟合补偿与二次拟合补偿之后的输出与理论值之间的误差值大小,来说明二次拟合后的精度及有效性。
图6是标定过程时的现场图。

图6 标定现场
图7是进行补偿之后,三轴加计实际输出与理论重力分量之间的误差曲线。图7中实线是经过二次补偿之后的标定误差,虚线则是一次拟合补偿之后未进行二次拟合补偿的误差曲线。显然经过二次拟合补偿后,标定误差下降了一个数量级。
图8是标定过程中,三轴上加速度计b系比力分别为1 gn时,并且补偿二次项之后的加计输出,和不进行二次项补偿时的结果对比。其中粗实线代表加速度计理论上敏感到的比力,实线为经过二次拟合补偿后的加速度计输出,虚线则是经过一次拟合补偿后的加速度计输出。由图7可以直观的看出,实线显然更加靠近理论值,即经过二次项补偿之后的加速度计输出精度明显优于未进行二次非线性系数补偿的结果。
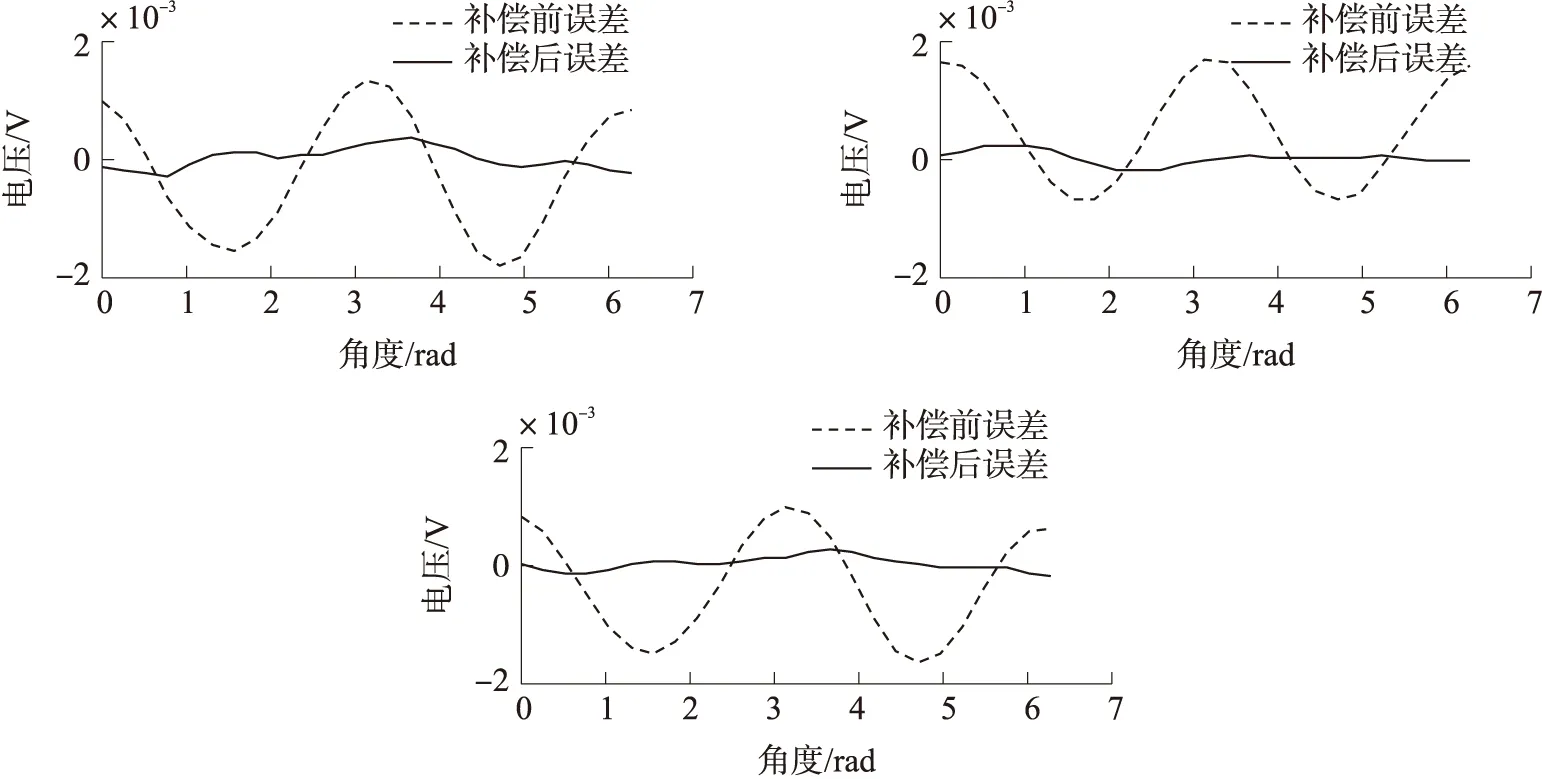
图7 标定误差
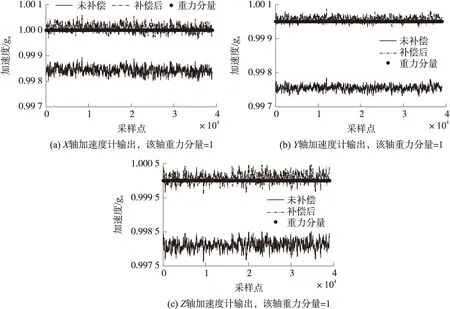
图8 加速度计补偿对比
3 基于线振动台的非线性系数的测量方法
将加速度计安装至线振动台上,线振动台能给加速度计一个正弦激励信号。设振动台给出的正弦激励振幅为A,频率为ω,代入式(1),变形可得:
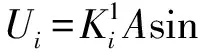
(12)
显然上式是正弦信号激励下的电压输出响应,其中包含与激励信号同频率的正弦信号,二倍频的余弦信号和二次非线性系数造成的常值漂移。理论上无论是计算常值漂移,还是进行频谱分析,都能求出二阶非线性系数。但是二次项造成的常值漂移通常非常小,就加速度计的分辨率而言,无法有效分离出真实的二阶非线性系数,安装误差也会影响二阶系数的计算。同时因为振动噪声等原因,通过频谱分离出二次项也非常困难。所以实际测得的加速度计二阶非线性系数不如通过转台标定补偿得到的参数可靠性高,且需要在转台之外借助线振动台进行测试,重复性差,标定流程繁琐,成本更加高昂。
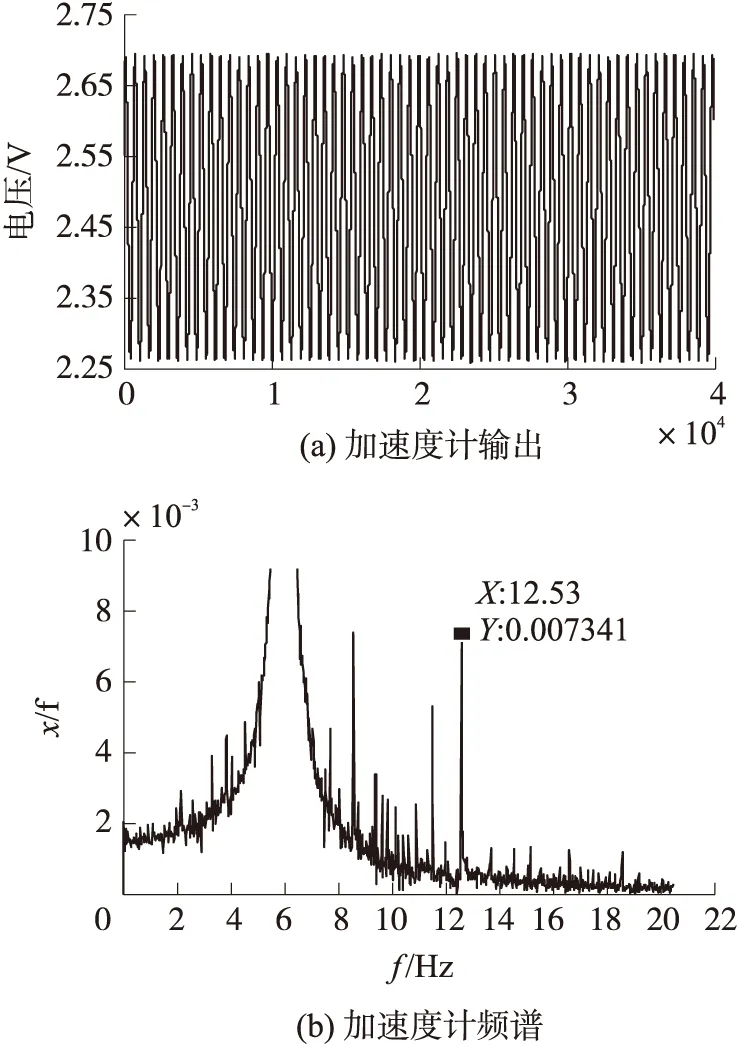
图9 加速度计振动台试验输出
图9是线振动台输入6Hz的正弦波角速率信号时的加速度计的输出曲线及去除了直流分量的频谱图像。图9(a)中的横坐标为采样点,纵坐标为输出电压(加速度计在6Hz正弦波激励下的时域输出),整体呈现为正弦波形式。图9(b)是加速度计经过傅里叶变换之后得到的频谱图,频率为0的直流分量不影响后续分析,为便于分析图像,已将其纵轴值设为0。
该加速度计经过多次转台试验测得其二次项均在0.006 5~0.006 6之间。从图9可以看出二倍频振幅大小为0.007 341,明显与转台计算出的结果存在较大的偏差,利用转台计算得出的二次非线性系数精度与重复性明显高于线振动台试验计算得出的结论。说明二次项的转台测试法优于线振动台测试法。
4 结束语
MIMU是惯性导航系统中的核心,其中各惯性传感器输出的准确性直接影响了最终导航解算的精确程度[13-14]。本文对MIMU中三轴加速度计含有二次项系数的输出模型进行了理论分析,根据理论分析建立了基于转台的加速度计多位置标定补偿计算二次项的试验方法,借助MATLAB软件建立了完整的数据处理方法。同时试验数据也与理论分析相符合。根据该方法与基于线振动台的测量计算方法进行的试验对比,说明了转台标定补偿法具有计算精度高、重复性好,且不受安装误差角的干扰。具有较强的工程实用价值。
[1]CN-JJF.微机电(MEMS)线加速度计校准规范[S]. 2013.
[2] 李杰,洪惠惠,张文栋,等. MEMS微惯性测量组合标定技术研究[J]. 传感技术学报,2008,21(7):1169-1173.
[3] 范成叶,李杰,景增增,等. 旋转弹用三轴加速度计安装位置误差标定补偿技术[J]. 传感技术学报,2013,(10):1352-1356.
[4] 吴畏,周坚鑫,刘晓东,等. 基于双轴倾斜法的加速度计分辨率测试方法[J]. 物探与化探,2015,39(z1):37-40.
[5] 李海兵,朱志刚,魏宗康,等. 高精度加速度计分辨率的动态估算方法[J]. 中国惯性技术学报,2012,20(4):496-500.
[6] 王洪,李磊民,黄玉清,等. 石英挠性加速度计零偏分析与建模方法[J]. 自动化仪表,2014,(11):13-16,19.
[7] 任顺清,冯士伟,马向斌,等. 加速度计的全组合标定方法[J]. 中国惯性技术学报,2007,15(6):760-764.
[8] 孙枫,曹通.基于Kalman滤波的加速度计十位置标定方法[J]. 系统工程与电子技术,2011,33(10):2272-2276.
[9] 郑益民.斜椭圆方程及其在工程中的应用[J]. 烟台师范学院学报(自然科学版),2003,19(4):258-260.
[10] 严恭敏.惯性仪器测试与数据分析.北京:国防工业出版社[M]. 2012:198-199.
[11] 龙达峰,刘俊,张晓明,等. 基于椭球拟合的三轴陀螺仪快速标定方法[J]. 仪器仪表学报,2013,34(6):1299-1305.
[12] 秦永元,张洪钺,汪叔华. 卡尔曼滤波与组合导航原理[M]. 电西北工业大学出版社,2012:11-13.
[13] 范建英,李杰,陈文蓉,等. 高精度数字陀螺仪安装误差标定与补偿方法[J]. 传感技术学报,2013,26(4):525-52.
[14] 田晓春,李杰,范玉宝,等. 一种微惯性测量单元标定补偿方法[J]. 传感技术学报,2012,25(10):1411-1415.

王一焕(1992-),男,汉族,中北大学硕士研究生,主要研究方向为MEMS器件误差补偿及导航算法研究等,wangyihuan1992@163.com;

李 杰(1976-),男,教授,博士生导师,主要研究方向为微系统集成理论与技术,惯性感知与控制技术,组合导航理论,计算几何与智能信息处理等,Lijie@nuc.edu.cn;

刘一鸣(1992-),男,汉族,中北大学硕士研究生,主要为MEMS器件误差补偿及导航算法研究等,liu1992326@163.com。
Study on the Method of Quadratic Nonlinearity Compensation of MEMS Accelerometer*
WANGYiyuan,LIJie*,LIUYiming,LANYang,LIWenhao
(1.Science and Technology on Electronic Test,North University of China,Taiyuan 030051,China)
Aiming at the problem that because of fixing error of the 3-axis accelerometer installed in the micro inertial measurement unit(MIMU)will enlarged in harsh cone movement situation,this paper puts forward a calibration-compensation method which is based on multi-position static rotation of the 3-axis position speed turntable.according to the establishment of the angle error compensation model to design the completed experiment process of calibration,and finally,calculating calibration factor matrix and accelerometer’s zero voltage accurately based on the method of nonlinear fitting data processing. according to the calibration experiment and error calculation contrast,this error of calibration method is one order of magnitude smaller than the previous one,improving the output accuracy of the accelerometer effectively,having significant engineering application meaning.
MIMU;calibration;second order linear coefficient;error compensation
项目来源:国家自然科学基金(51575500)
2016-07-13 修改日期:2016-11-18
V241.62
A
1004-1699(2017)03-0418-07
C:7230
10.3969/j.issn.1004-1699.2017.03.015
