三维传感网空间RSS与AOA混合测量的精确定位方法*
2017-04-14严长虹
严长虹,马 静
(1.南京航天航空大学经济管理学院,南京 210016;2.盐城工学院信息学院,江苏 盐城 224000;)
三维传感网空间RSS与AOA混合测量的精确定位方法*
严长虹1,2*,马 静1
(1.南京航天航空大学经济管理学院,南京 210016;2.盐城工学院信息学院,江苏 盐城 224000;)
由于位置坐标参数的增加,三维传感网空间的定位难度较二维平面有所增大。单一的依靠接收信号强度(RSS)确定节点位置坐标的方法将使定位的不确定性增加,定位误差也较大。新型的阵列与智能天线的出现为节点间的到达角度(AOA)测量提供了方便,为此本文提出了一种三维传感网空间RSS与AOA混合测量的精确定位方法。将采用混合测量建立的非线性优化模型转化为线性方程,分别提出了节点位置坐标估计的非约束线性最小二乘(ULLS)及约束线性最小二乘(CLLS)方法。仿真测试了所设计算法的有效性,分析了不同测量噪声对位置坐标估计误差的影响。仿真表明所设计的ULLS和CLLS方法的计算速度快,相比于ULLS方法,采用约束后的CLLS方法的定位误差更小。在较小测量噪声范围内,ULLS和CLLS估计方法具有较高的稳定性和定位精度。
传感网;定位;接收信号强度;到达角度;线性最小二乘
无线传感器网络(简称传感网)近来已被大量应用于各种各样的环境监测场所,其中传感网的定位技术已成为其应用推广的关键因素[1-2]。传统的GPS系统由于能耗与价格高、体积大等众多缺陷难以适用于传感网定位。为适应传感网定位低成本的要求,更多的定位方法关注于传感网的节点射频(RF)与无线通信功能。利用节点间的无线射频通信特点,开发性能优越的节点定位技术已成为传感网定位内容的研究热点。
建立于节点间的射频通信功能基础上,已有大量的研究关注于如何开发有效的传感网定位技术。通常来说,在传感网定位技术中,为估计未知位置坐标的节点(未知节点),需要采用一定数量已知位置坐标的信标节点建立节点间的距离约束关系。常用的测距技术到达时间(TOA)[3-4]、到达时间差(TDOA)[5]、到达角度(AOA)[6]与信号接收强度(RSS)[7-8]等。为充分利用上述各种测距方法各自的优缺点,混合定位技术也是近来的研究热点[9]。
通过建立的节点间距离约束优化模型,已有大量关于传感网的定位算法,如极大似然(ML)估计[10]、线性代数法[11]及凸优化等实现方法。ML估计方法的数值计算方法依赖于初始解的选择,若初始解选择不合适,有可能陷入局部最优,为此提出了线性代数法及凸优化方法。凸优化方法(常见方法包括半正定(SDP)[12-13]和二阶锥规划(SOCP)[14])将优化模型松弛为凸优化问题,是当前传感网定位方法中比较流行的一种方法。凸优化方法进行了松弛,导致了定位结果非最优,并且凸优化函数具有较多的变量和等式约束,计算复杂度较高。为降低计算复杂度,线性代数法将计算结果直接表示为代数解,计算过程较快。
由于未知参数较多,三维空间较二维平面的传感网定位难度有所增加。在三维空间上,若采用单一的测距方法,所需要的信标节点数量也比二维平面多,定位结果的不确定性也较大。节点间以无线射频方式进行相互通信,信号接收强度RSS值随传输路径的延长而衰减。在无线传感器网络领域,接受信号强度(RSS)距离测量具有较高性价比,并且RSS定位方法无需额外硬件,实现简单,具备低功耗、低成本等特点。电子罗盘或者视觉传感器为节点间的AOA提供了可能,但需要额外的硬件配置,增加了节点的硬件成本。随着新型阵列技术和智能天线的不断发展,节点间的AOA测量成本在不断降低,这为节点间的AOA测量提供了广阔的空间。因此,通过节点间的RSS和AOA混合测量实现三维传感网节点定位,具有较高的应用前景[15]。
基于节点间的RSS和AOA混合测量技术,本文提出了三维传感网空间的节点位置坐标精确估计方法。将RSS与AOA混合测量的优化模型转化为线性方程,推导了节点位置坐标估计的非约束线性最小二乘(ULLS)和约束线性最小二乘(CLLS)方法,并与模型的克拉美罗(CRLB)下界值进行了比较。设计的混合测量方法实现三维传感网空间定位所依赖的信标节点数量少,定位精度高。本文第1部分首先介绍了RSS与AOA混合定位的问题描述;第2部分推导了ULLS和CLLS的计算方法;第3部分推导了模型的克拉美罗(CRLB)下界值;第4部分为仿真与分析;最后部分为结论。
1 问题描述
考虑在三维空间上分布着N个已知位置坐标的信标节点,其坐标位置分别为ai=[aixaiyaiz]T,(i=1,2,…,N)。同时在该空间区域内存在待定位的未知节点,其位置坐标表示为x=[xxxyxz]T。将未知节点与信标节点i间的RSS测量值表示为pi,根据RSS测距的对数衰减模型,有以下关系式
pi=p0-10βlgdi+εii=1,2,…,N
(1)

在三维平面上,未知节点的位置坐标参数包括x、y、z 3个方向。仅仅依靠与各信标节点RSS测量获取未知节点位置坐标的方法,定位结果有可能不可靠。并且RSS测量噪声较大,定位结果的不确定性也随之增加。为减少定位误差和保证三维空间下定位结果的可靠性,未知节点同时也测量与各信标节点间的方向角和仰角,如图1所示。
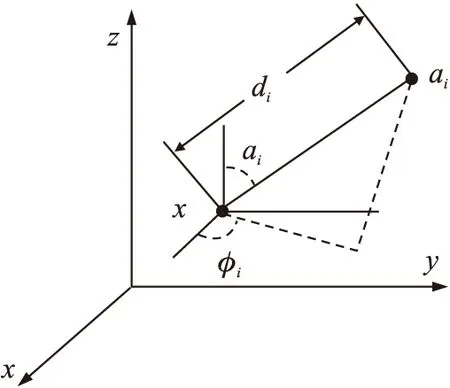
图1 未知节点与信标节点间的AOA测量示意图
假设未知节点与信标节点i间的方向角及仰角分别为φi及αi,i=1,2,…,N。根据节点间的地理位置关系,方向角φi及仰角αi有以下关系式,
(2)
(3)
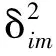
为估计未知节点位置坐标x,以RSS及AOA混合测量为已知值,极大似然(ML)估计通过极大化下列表达式
(4)

式(4)建立的优化函数为非线性方程,其数值计算方法依赖于初始解的选择。若初始解选择的不合适,将有可能陷入局部最优,使得定位结果发生严重偏差,为此本文将非线性优化方程转化为线性方程,采用两步计算方法精确计算未知节点位置坐标。
2 线性最小二乘估计法
考虑在较小噪条件下,对测量方程进行近似线性化处理,将式(4)所描述的非线性优化模型转化为线性方程,所设计的计算方法分成两步:非约束线性最小二乘法ULLS(Unconstrained Linear Least Square)及约束线性最小二乘法CLLS(Constrained Linear Least Square)。
2.1 非约束线性最小二乘法
对式(1)进行移位变换,则其可以改写为
(5)
式中:i=1,2,…,N。考虑在较小噪声范围内,对式(5)右边采用泰勒级数展开,忽略高阶项,将式(5)变换为

(6)

(7)
由于di=‖x-ai‖,对式(7)展开,有表达式
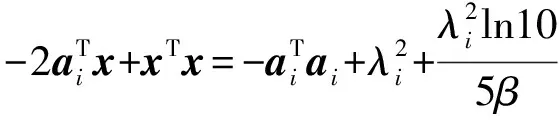
(8)
式(8)表示了转化后的RSS测量方程,i=1,2,…,N。令z=[xTxTx]T,可将式(8)写成线性矩阵形式
A1z=b1+η1
(9)

对方向角测量方程进行转化,即对式(2)进行变换,有表达式
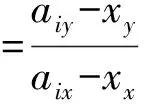
(10)
对式(10)右边采用泰勒级数展开,忽略高阶项,有表达式
-sinφixx+cosφixy=-sinφiaix+cosφiaiy+
(11)
式(11)表示了转化后的方向角方程,i=1,2,…,N。
同样地可将式(11)写成线性矩阵形式
A2z=b2+η2
(12)
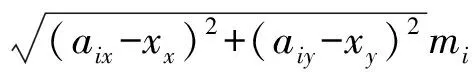
同样对仰角测量方程(3)进行变换,有表达式
dicos(αi-ni)=aiz-xz
(13)
将式(6)代入式(13),并采用泰勒级数展开,忽略高阶项,有表达式
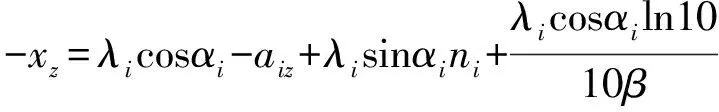
(14)
式(11)表示了转化后的仰角方程,i=1,2,…,N。
同样地可将式(14)写成线性矩阵形式
A3z=b3+η3
(15)
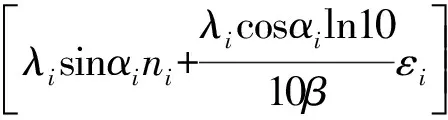
联合RSS方程(9)、方向角方程(12)及仰角方程(15),建立统一的矩阵形式
Az=b+η
(16)
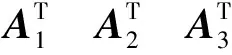
根据线性最小二乘平方原理,参数z的估计值为

(17)
式(17)中维度为3N×3N的矩阵Σ为权重矩阵,其值为Ση=E(ηTη),其值进一步表示为
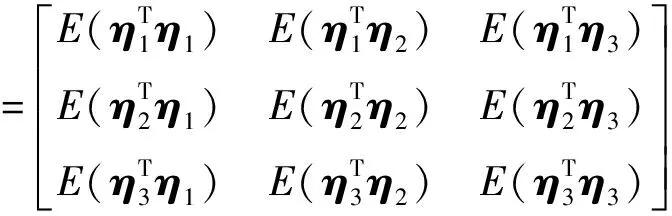
(18)


(19)
假设参数z的估计误差为Δz,其值为
Δz=(ATΣ-1A)-1ATΣ-1η
(20)
则估计误差Δz的方差为
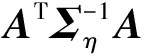
(21)
从参数z提取出z(1:3)即为被定位未知节点的位置坐标。上述求解过程并未考虑z=[xTxTx]T中最后元素与前3个元素值间的相互约束关系,因此把该计算方法称为RSS与AOA混合定位问题的非约束线性最小二乘(ULLS)方法。式(17)得到了被定位未知节点坐标的近似估计值,可利用向量z=[xTxTx]T元素间的相互约束关系计算未知节点位置坐标精确值。
2.2 约束线性最小二乘法
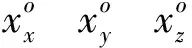
(22)
式中:z(k)、Δz(k)表示了向量z、Δz的第k个元素,k=1,2,3,4。将式(22)表示为线性矩阵形式
Guo=h+γ
(23)

根据线性最小二乘平方原理,向量uo的无偏估计为

(24)
式中:维度为4×4的权重矩阵Σγ值为
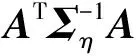
(25)
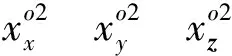

(26)
将以式(26)表示的计算过程考虑了参数z中元素间的相互约束关系,得到了精确的定位结果,将此计算方法称为RSS和AOA混合定位问题的约束线性最小二乘(CLLS)方法。
3 模型的克拉美罗下界(CRLB)
CRLB下界值为模型待估参数的无偏估计提供了误差方差的下界,设未知节点位置坐标参数x的估计误差方差为cov(x),则根据克拉美罗下界理论,有关系式cov(x)≥F-1,里F为待估位置坐标参数x的FIM(Fisher Information Matrix)的表示,矩阵F表示为
(27)
p表示了模型的测量参数,包括RSS、方向角和仰角,lnP(p|x)为概率密度函数,可以表示为
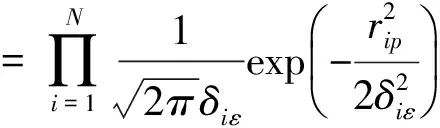
(28)
对式(28)两边取对数并定义向量rp、rφ及rα,rp=[r1pr2p…rNp]T,rφ=[r1φr2φ…rNφ]T,rα=[r1αr2α…rNα]T,有如下表达式

(29)

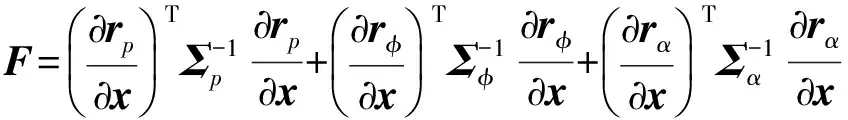
(30)

(31)
(32)
则根据CRLB无偏估计下界理论有
CRLB([x]r)=[F-1]r,rr=1,2,3
(33)
式中:[F-1]r,r表示F的逆矩阵的第r行、第r列元素值;CRLB([x]r)表示向量x的第r行元素的CRLB无偏估计下界。
4 仿真分析

4.1 噪声对定位误差的影响
仿真首先测试了上述ULLS、CLLS计算方法下的RMSE定位误差,并与文献[13]所介绍的SDP方法进行了比较。保持方向角噪声δm及仰角噪声δn都等于1度,同时调整RSS测量噪声δε从0.2 dB到2 dB之间变化,图2(a)绘出了不同算法下的RMSE定位误差随RSS测量噪声变化关系。由图2(a)可见,随着RSS测量噪声的增大,RMSE定位误差也随之增大。当RSS测量噪声等于0.2 dB时,所设计ULLS方法的RMSE定位误差为1.0 m,而CLLS方法的RMSE定位误差仅为0.67 m。相比于ULLS方法,采用约束后的CLLS方法的定位误差有较大减少,更加接近于定位结果的CRLB下界值。相比于SDP方法,ULLS方法的定位误差较大,而CLLS方法的定位误差较SDP方法小。当RSS测量噪声δε等于0.2 dB时,SDP方法的RMSE定位误差为0.86 m,该值介于ULLS和CLLS方法的定位误差之间。
仿真同时测试了方向角测量噪声对定位误差的影响,保持RSS测量噪声δε等于0.2 dB及仰角噪声δn等于1度,图2(b)绘出了不同算法下的定位误差随方向角噪声变化关系。由图2(b)可见,随着方向角噪声δm的增加,RMSE定位误差也随之增大。当方向角噪声等于0.5°时,ULLS、SDP及CLLS的定位误差相差不大。但当方向角噪声增加到5°时,ULLS方法的定位误差达到了4.0 m,而SDP方法的定位误差到了2.7 m,CLLS方法的定位误差仅为1.3 m。与图2(a)同样的分析结果发现,采用约束CLLS方法的定位误差比ULLS及SDP方法的定位误差更小。
同样地保持RSS测量噪声δε等于0.2 dB及方向角噪声δm等于1°,图2(c)绘出了不同算法下的定位误差随仰角测量噪声变化关系。相比于方向角测量噪声对定位误差的影响,仰角对定位误差的变化较为平缓。由图2(b)可见,当仰角测量噪声从0.5°增大到5°时,ULLS方法的定位误差从0.75 m增大到了1.42 m,而CLLS方法的定位误差从0.45 m增大到了0.96 m,CLLS方法的定位误差比ULLS方法的定位误差更接近于CRLB下界值。
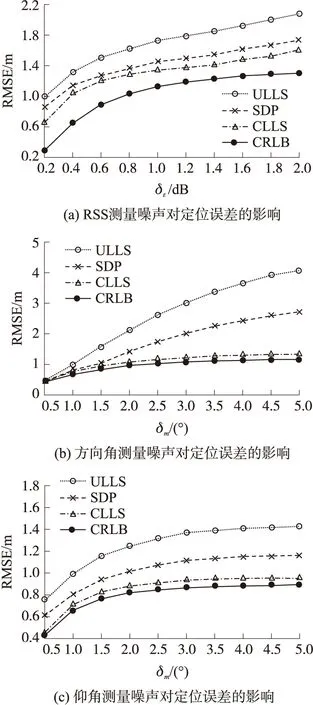
图2 测量噪声对定位误差的影响
4.2 路径衰减指数的影响
设置测量噪声δε等于0.2dB、方向角噪声δm及仰角噪声δn都等于1°,调节路径衰减指数β值从典型值2~5之间变化,图3绘出了路径衰减指数对定位误差的影响。随着路径衰减指数β的增大,定位误差逐渐减少。当路径衰减指数β等于2时,ULLS、SDP及CLLS的定位误差分别为1.32m、1.15m及1.09m;而当路径衰减指数β增加到5时,ULLS、SDP及CLLS的定位误差分别减少到0.89m、0.71m及0.55m。
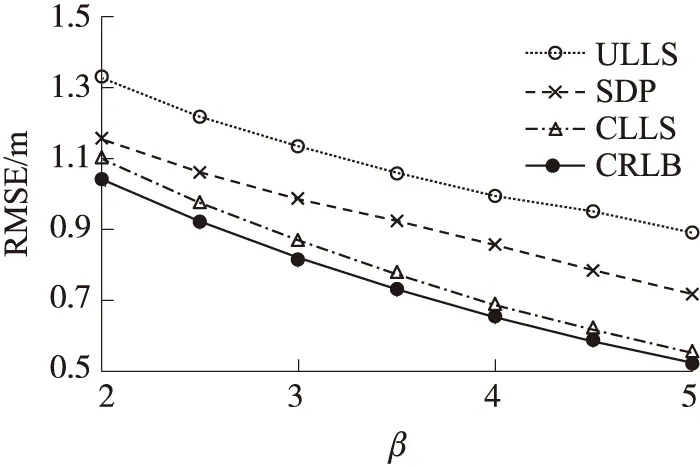
图3 路径衰减指数对定位误差的影响
5 结论
通过未知节点与信标节点间的RSS与AOA混合测量,本文提出了一种三维传感网空间未知节点位置坐标的精确估计方法。将非线性优化模型转化为线性方程,得到了未知节点位置坐标的线性ULLS解法。并对ULLS解法下的定位结果优化为精确的CLLS结果,保证了定位精度。设计的混合测量定位方法所依赖的信标节点数量少,定位精度与可靠性都较高。与文献所介绍的SDP方法相比较,所设计的ULLS、CLLS线性估计方法计算复杂度低,运算速度快。相比于SDP方法,约束后的CLLS方法的定位误差更小,更加接近于定位结果的CRLB下界值。但仿真分析也发现,本文所提出的ULLS及CLLS亦有一定的局限性,尤其是当测量噪声较大时,有可能导致测量矩阵A奇异,无法准确定位未知节点。
[1] He Yuan,Liu Yunhao,Shen Xingfa,et al. Noninteractive Localization of Wireless Camera Sensors with Mobile Beacon[J]. IEEE Transactions on Mobile Computing,2013,12(2):333-345.
[2] 叶苗,王宇平.一种新的容忍恶意节点攻击的无线传感器网络安全定位方法[J]. 计算机学报,2013,36(3):532-544.
[3] Wang Yuan,Ma Shaodan,Philip Chen C L. TOA-Based Passive Localization in Quasi-Synchronous Networks[J]. IEEE Communications Letters,2014,18(4):592-595.
[4] Hong Shen,Zhi Ding,Soura Dasgupta,et al. Multiple Source Localization in Wireless Sensor Networks Based on Time of Arrival Measurement[J]. IEEE Transactions on Signal Processing,2014,62(8):1938-1949.
[5] Yang L,Ho K C. An Approximately Efficient TDOA Localization Algorithm in Closed-Form for Locating Multiple Disjoint Sources with Erroneous Sensor Positions[J]. IEEE Transactions on Signal Processing,2009,57(12):4598-4615.
[6] Shao Huajie,Zhang Xiaoping,Wang Zhi. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables[J]. IEEE Transactions on Signal Processing,2014,62:2580-2594.
[7] 袁鑫,吴晓平,王国英. 线性最小二乘法的RSSI定位精确计算方法[J]. 传感技术学报,2014,27(10):1412-1417.
[8] Xu Yaming,Zhou Jianguo,Zhang Peng. RSS-Based Source Localization when Path-Loss Model Parameters are Unknown[J]. IEEE Communications Letters,2014,18(6):1055-1058.
[9] Chan Y T,Chan F,Read W,et al. Hybrid Localization of an Emitter by Combining Angle-of-Arrival and Received Signal Strength Measurements[C]//IEEE CCECE,2014:1-5.
[10] Sheng Xiaohong,Hu Yuhen. Maximum Likelihood Multiple-Source Localization Using Acoustic Energy Measurements with Wireless Sensor Networks[J]. IEEE Transactions on Signal Processing,2005:53(1):44-53.
[11] So H C,Lin Lanxin. Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization[J]. IEEE Transactions on Signal Processing,2011,59(8):4035-4040.
[12] Pratik B,Tzu-Chen L,Kim-Chuan T,et al. Semidefinite Programming Approaches for Sensor Network Localization with Noisy Distance Measurements[J]. IEEE Transactions on Automation Science and Engineering,2006,3(4):1-11.
[13] Slavisa T,Marko B,Rui D. 3-D Target Localization in Wireless Sensor Network Using RSS and AoA Measurements[J]. IEEE Transactions on Vehicular Technology.DOI 10.1109/TVT.2016.2589923.
[14] Ghasem N S,Michael B S,Lutz L. Second Order Cone Programming for Sensor Network Localization with Anchor Position Uncertainty[J]. IEEE Transactions on Wireless Communication,2014,13(2):949-963.
[15] Slavisa T,Milica M,Marko B,et al. Hybrid RSS-AoA Technique for 3-D Node Localization in Wireless Sensor Networks[C]//IEEE IWCMC,2015:1277-1282.

严长虹(1980-),讲师,在读博士,主要研究方向为无线传感器网络、信号分析与处理、网络安全等,在国内外重要会议及期刊上发表论文十多篇;

马 静(1966-),教授,博士生导师,主要研究领域包括信息企业化、知识管理与知识管理系统、电子商务、国防科技情报、复杂网络与网络舆情、大数据分析等。
Precise Positioning Method with Hybrid RSS and AOA Measurements in 3-D WSN Space*
ChanghongYan1,2*,JingMa1
(1.College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.School of Information Engineering,Yancheng Institute of Technology,Yancheng Jiangsu 224000,China)
It is more difficult for the 3-D WSN space localization compared with 2-D plane due to the addition of the position coordinate parameters. The method to locate a sensor node will make the increasing of positioning uncertainty by the single received signal strength(RSS),and the position error is also big. The emergence of new array and smart antenna provides the convenience of the arrival of angle(AOA)measurements,so a precise positioning method is proposed by using the hybrid RSS and AOA measurements in 3-D WSN space. The built nonlinear optimization model using the hybrid measurements is converted into the linear equations,then the unconstrained linear least squares(ULLS)and constrained linear least squares(CLLS)methods are put forward for the estimation of the node position coordinates. The simulations show that the ULLS and CLLS run fast and the positioning error of CLLS is less than that of ULLS due to the constraint condition. In a small range of measurement noise,the estimation methods of ULLS and CLLS have high stability and positioning accuracy.
wireless sensor networks;localization;received signal strength;arrival of angle;linear least squares
项目来源:国家自然科学基金项目(71373123);江苏高校哲学社会科学研究重点项目(2015ZDIXM007);南京航空航天大学基本科研业务费重大项目(NP201630X)
2016-08-17 修改日期:2016-11-19
TP393.0
A
1004-1699(2017)03-0450-06
C:6150;7110;5210
10.3969/j.issn.1004-1699.2017.03.019
