基于卡尔曼滤波的永磁同步电动机位置检测

陈达波

(重庆水利电力职业技术学院，永川 402160)

基于卡尔曼滤波的永磁同步电动机位置检测

陈达波

(重庆水利电力职业技术学院，永川 402160)

研究了一种基于卡尔曼滤波的永磁同步电动机位置检测方案。在永磁同步电动机的矢量控制中，转子位置的检测精度对于控制性能十分关键。低成本的应用场合中，常采用3个空间互差120°的开关型霍尔来检测当前转子位置，但是霍尔安装误差、磁场分布不均匀等原因均会造成霍尔传感器之间的不一致，进而产生位置检测偏差。针对该问题，介绍了一种基于卡尔曼滤波的检测方案，结合霍尔的测量值，对真实的转速和位置进行观测。同时考虑了角加速度，对加减速段进行处理，使之数学模型更贴合实际。仿真和实验表明，所介绍的位置检测方案能够有效提高检测精度。

永磁同步电动机；位置检测；霍尔传感器；卡尔曼滤波

0 引 言

永磁同步电动机(以下简称PMSM)通过在电机的转子上安装永磁体取代了励磁绕组，可以减小电机体积并且提高性能与可靠性，应用领域越来越广泛[1]。

PMSM的控制性能十分依赖于转子位置检测的准确性。在典型的调速场合中，常采用光电编码器或者旋转变压器这样高精度的传感器。但是在对成本或安装有限制的应用场合中，开关型霍尔传感器更为常用。3个霍尔传感器空间中相差120°排列，每个传感器根据当前N极或S极所处的位置而产生方波信号。因此在一个电周期中，开关霍尔能产生6个脉冲，分辨率较低。为了提高其位置检测的精度，许多学者进行了研究[2-7]。

文献[3-5]提出了一种基于零阶泰勒展开的位置计算方法，结构简单易于实施，但是霍尔传感器之间的间隔不均匀会导致计算转速有误差，且在脉冲发生的时候位置不连续。文献[6]使用全阶观测器来估计位置。该观测器能在全速范围内估计转子位置。文献[7]采用矢量叉乘算法来提高计算性能，同时提出了调整霍尔的偏置以消除机械上的不匹配。但是这些方法都是基于电机的机械方程，因此需要用到机械参数，如转动惯量和转矩。

本文提出一种基于卡尔曼滤波的永磁同步电动机位置检测方法。以转速和位置作为状态量，以霍尔传感器的检测值作为观测量建立模型。该方法将霍尔传感器的不一致作为噪声予以消除，从而减小了位置检测的误差。在加减速过程中，模型存在直流偏置误差，对此采用量测扩增法对转子的角加速度同时进行观测，提高了模型的准确性。仿真和实验结果表明，该位置检测方案能有效提高检测精度。

1 传统位置检测方法

3个开关型霍尔传感器安装在PMSM的定子内。当转子转动时，N极和S极分别在霍尔传感器中产生高电平和低电平，从而每个霍尔传感器在一个电周期内输出180°方波。当3个霍尔传感器在空间中相差120°时，每60°会出现一个电平变化，因此该检测方法的分辨率为60°。转子的角速度ωhall可以表达成式(1)，其中ΔT是两个霍尔电平变化之间的时间间隔。转子的位置可以由式(2)得到，其中T是采样时间，θhall(k)是k时刻计算得到的转子电角度。值得注意的是，这里π/3的角度间隔是理想的情况。在实际中，由于传感器电路不一致、磁场分布不均匀和机械安装误差等原因，霍尔电平变化之间的角度间隔不是准确的π/3。

θhall(k+1)=θhall(k)+ωhall·T

如图1所示，在非理想情况下，霍尔电平变化之间的角度间隔不是准确的π/3。因此，在霍尔电平发生变化的时候，θhall发生了阶跃。在极对数较多的情况下，不能用简单的补偿方法来消除此误差。

图1 非理想情况下的霍尔位置检测

2 基于卡尔曼滤波的位置检测

2.1 卡尔曼滤波

卡尔曼滤波器是由美国学者R. E. Kalman提出的最小均方误差准则下的最优线性估计器，具有良好的抗干扰性能，可以用来滤除线性系统中的随机误差。先建立系统的状态方程和观测方程如下：

(3)

(4)

式中：w(k)表示系统的过程噪声;v(k)表示系统的观测噪声;x(k)为状态向量;U(k)为输入向量;Y(k)为观测向量。

那么，系统的Kalman滤波求解过程如下：

1) 计算状态向量的预测值：

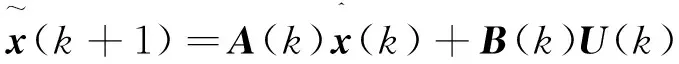
(5)

2) 计算误差协方差矩阵的预测值：

(6)

3) 更新卡尔曼增益矩阵：

(7)

4) 根据观测值，校正当前状态向量的最优估计值：

(8)

5) 校正得到误差协方差矩阵的最优估计值：

(9)

假设转子转速ωr在采样时间T内不变，那么式(1)和式(2)可以表达成如下离散形式。

(10)

(11)

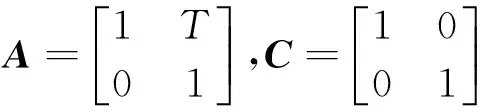
(13)

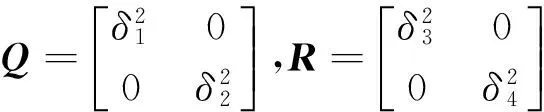
(14)

式中：Q和R是过程噪声和观测噪声的协方差矩阵。

此处，将转子的位置和转速作为状态变量进行估计，将霍尔检测到的位置和转速作为观测值用于调整估计值。由于霍尔传感器不一致导致的霍尔检测误差则作为噪声被滤除。实际上，卡尔曼滤波只能消除白噪声，而霍尔检测误差不是白噪声，因此该方法不能完全消除误差，但是从仿真和实验结果来看，已经能够较大提高检测精度。

2.2 加减速段的处理

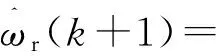
加减速的时候，有：

(15)

当采用匀加减速时，有：

α(k+1)=α(k)

(16)

从而，加减速段的状态方程和观测方程可以改写：

(17)

(18)

在加减速段，式(17)、式(18)描述的系统更符合实际的模型;同时，该系统在匀速段也是成立的。不难看出，匀速段估计得到的状态变量α(k)=0。

3 仿真和实验验证

为了验证上述基于卡尔曼滤波的永磁同步电动机位置检测方法的有效性，在一台多对极的PMSM上进行了实验。PMSM采用的矢量控制方式，控制框图如图2所示。电机运行时，采用MTPA的控制方法来提高电流利用率。PMSM中安装的3个霍尔传感器获得3路方波信号，按照式(1)和式(2)得到ωhall和θhall之后，由卡尔曼滤波算法获得估计的转速和位置，并用于速度反馈和坐标变换。

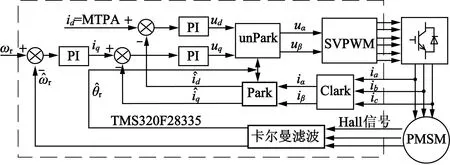
图2 PMSM矢量控制框图

3.1 仿真结果

图3是速度不变时的仿真结果。霍尔传感器的布置不是相差准确的120°，而且N极和S极也不是均匀分布。可以看到，如果使用传统的霍尔检测方法，检测到的转子位置会出现不连续，而且误差较大，最大误差达到了20°。当采用卡尔曼滤波算法检测位置时，检测结果是连续的，且误差大幅减小，约为5°。

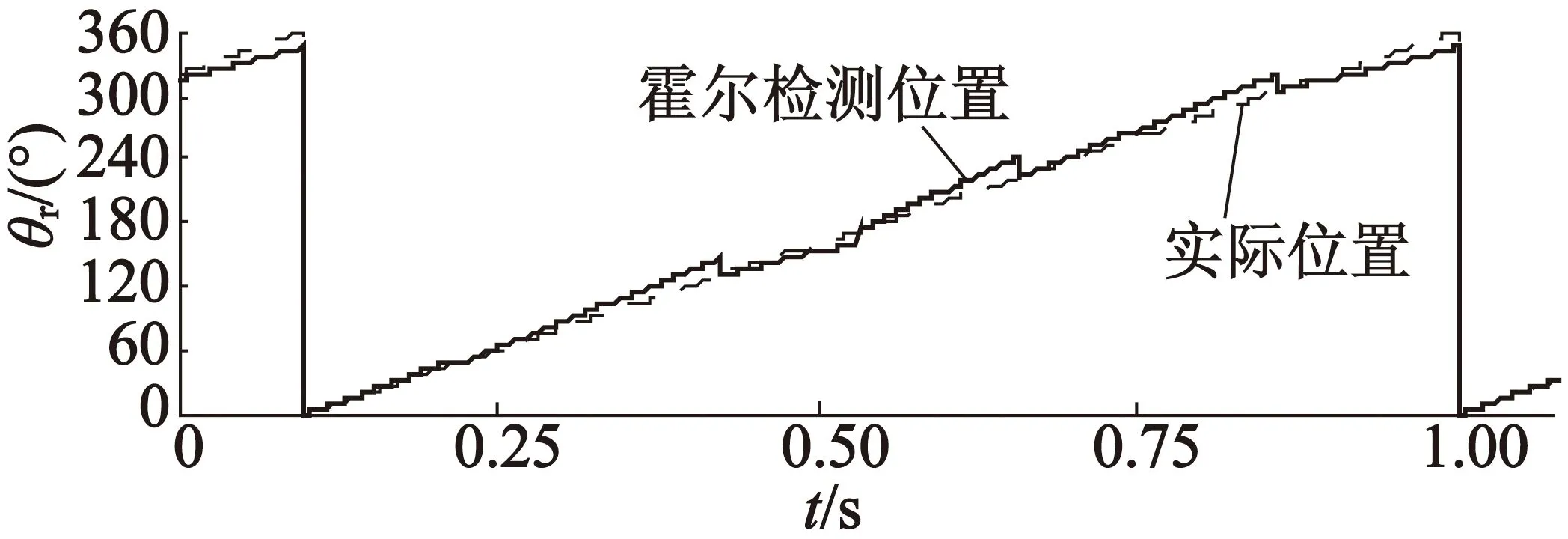
(a) 霍尔检测位置

(b) 卡尔曼滤波检测位置

(c) 位置检测误差

图4是速度变化时的仿真结果。运行频率从1 Hz加速到4 Hz。位置检测采用卡尔曼滤波算法。图4(a)是未考虑角加速度时的结果，此时状态方程和实际误差较大，因此估计结果也存在明显的误差，误差约为30°。当将角加速度加入状态变量一起进行观测时，位置估计结果的误差减小到8°。这表明，本文提出的基于卡尔曼滤波的位置检测方法能提高检测精度，且考虑角加速度时能够获得更好的动态性能。

(a) 未考虑角加速度时的检测结果

(b) 考虑角加速度时的检测结果

3.2 实验结果

本文搭建的实验平台采用TI公司的32位浮点处理器TMS320F28335作为控制芯片，系统时钟设为150 MHz。驱动器的母线供电电压为直流24 V。逆变电路由分立MOS管FDP120N10搭建，MOS管的驱动芯片采用Fairchild公司的FAN7888。用于矢量控制的电流采样电路由Allegro公司的电流霍尔传感器ACS712和运放电路构成。3个开关型霍尔的信号进入DSP的IO口。为了验证算法的位置检测性能，安装了1 024线的光电编码器作为对比，光电编码器的信号进入DSP的QEP口。DSP的数据再经过UART端口传输到PC，再由MATLAB绘制出实验曲线。实验平台如图5所示。

图5 实验平台实物图

实验结果如图6所示。实验中，让电机的转速从300 r/min升速到600 r/min,再减速到300 r/min，如图6(a)所示。在这个过程中，传统的霍尔位置检测方法误差较大，约为10°。若采用本文提出的基于卡尔曼滤波的检测方法，速度稳定时的检测误差仅为3°，动态时的误差也比传统方法要小。因此，仿真和实验结果都表明，本文提出的PMSM位置检测方法是有效的。

(a) 转速指令

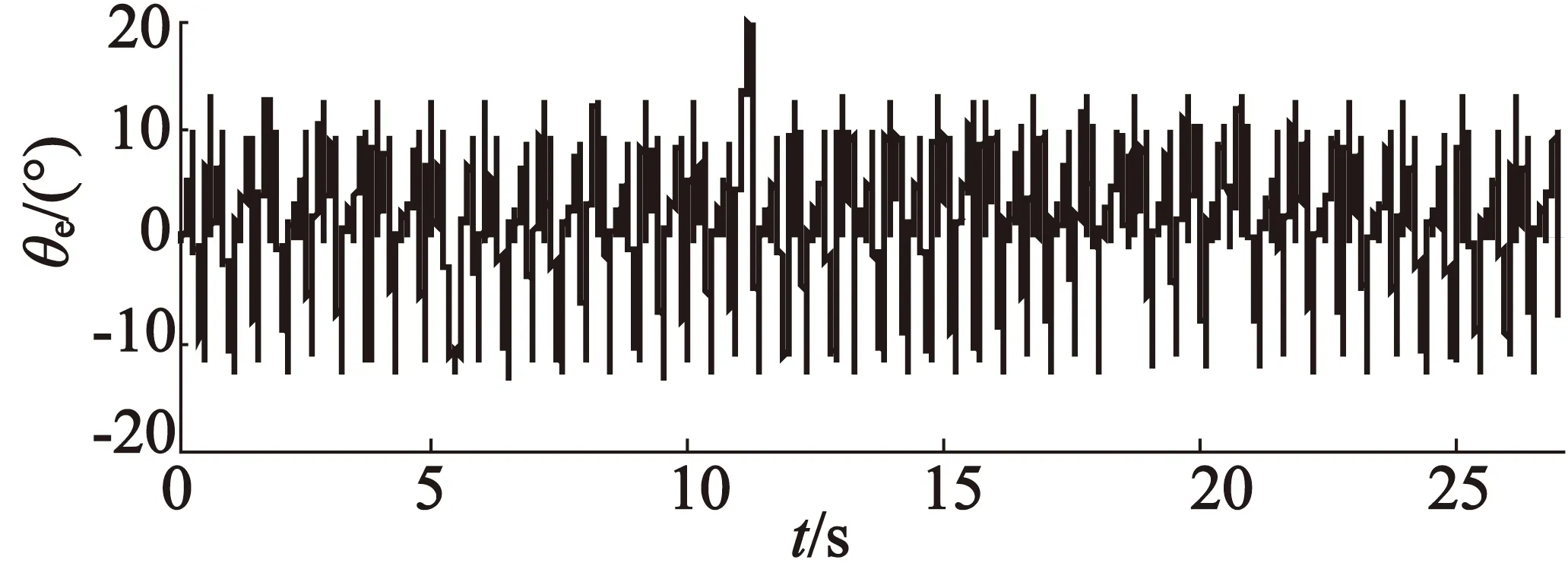
(b) 传统霍尔位置检测结果

(c) 本文方法检测结果

4 结 语

本文针对PMSM的转子位置检测，提出一种采用开关型霍尔传感器和卡尔曼滤波算法的检测方法。首先通过霍尔传感器获得转子转速和位置的测量值，但传感器的不一致会产生测量误差。利用卡尔曼滤波算法对测量值中的测量误差予以滤除，同时对角加速度进行观测，减小了建模误差。仿真和实验结果表明，本文提出的方法在稳态和动态下都有较高的位置检测精度。

[1] 王成元,夏加宽,杨俊友,等电机现代控制技术[M].北京：机械工业出版社,2006.

[2] KIM S Y,CHOI C,LEE K,et al.An improved rotor position estimation with vector-tracking observer in PMSM drives with low-resolution hall-effect sensors[J].IEEE Transactions on Industrial Electronics,2011,58(9):4078-4086.

[3] FANG J,ZHOU X,LIU G.Instantaneous torque control of small inductance brushless DC motor[J].IEEE Transactions on Power Electronics, 2012,27(12):4952-4964.

[4] FENG Z,ACARNLEY P P.Extrapolation technique for improving the effective resolution of position encoders in permanent-magnet motor drives[J].IEEE/ASME Transactions on Mechatronics,2008,13(4):410-415.

[5] BECCUE P B,PEKAREK S D,DEKEN B J,et al.Compensation for asymmetries and misalignment in a hall-effect position observer used in PMSM torque-ripple control[J].IEEE Transactions on Industry Applications,2007,43(2):560-570.

[6] TESCH T R,LORENZ R D.Disturbance torque and motion state estimation with low-resolution position interfaces using heterodyning observers[J].IEEE Transactions on Industry Applications,2008,44(1):124-134.

[7] DALALA Z M,CHO Y,LAI J S.Enhanced vector tracking observer for rotor position estimation for PMSM drives with low resolution Hall-effect position sensors[C]//Electric Machines & Drives Conference.IEEE,2013:484-491.

Position Detection of Permanent Magnetic Synchronous Motor Based on Kalman Filter

CHENDa-bo

(Chongqing Water Resources and Electric Engineering College,Yongchuan 402160,China)

A method of position detection of permanent magnetic synchronous motor (PMSM) based on Kalman filter was proposed. The accuracy of rotor position detection is very important for the vector control performance of PMSM. In low cost applications, three binary-type Hall sensors arranged 120° apart were used to detect the rotor position. However, installation error and non-uniform flux distribution could lead to the inconformity of Hall sensors, and then position detection error was generated. To tackle this problem, a detection scheme based on Kalman filter was proposed. The actual speed and position were observed combined with measured value by Hall sensors. Meanwhile, the accretion period was specially deal with, so that the model was more aligned with the reality. In the end, experimental results show that the proposed scheme can improve the position detection accuracy.

permanent magnet synchronous motor (PMSM); position detection; Hall sensor; Kalman filter

2016-08-04

TM341;TM351

A

1004-7018(2017)03-0062-03

陈达波(1983-)，男,硕士，讲师，研究方向为电力系统自动化。