基于超螺旋二阶滑模的PMSM-DTC系统研究

张苏英,马贺明,墨昭瑾,李林静,刘慧贤

(河北科技大学电气工程学院, 河北石家庄 050018)

基于超螺旋二阶滑模的PMSM-DTC系统研究

张苏英,马贺明,墨昭瑾,李林静,刘慧贤

(河北科技大学电气工程学院, 河北石家庄 050018)

针对传统永磁同步电机直接转矩控制系统(PMSM-DTC)易受参数变化影响及转矩脉动大的问题，提出在系统中采用空间电压矢量调制技术(SVPWM)代替传统的正弦脉宽调制(SPWM)，引入控制率为超螺旋算法的二阶滑模变结构，以定子磁链和转矩作为被控对象设计控制器代替传统系统中的PI控制器。仿真结果表明，该策略不仅有效消除了一阶滑模存在的抖振问题，明显减小了系统中定子磁链和转矩脉动，且具有较强的速度跟踪能力，对负载扰动和参数变化等不确定性具有很强的鲁棒性，因此可以很好地应用在电机控制方面。

鲁棒控制；永磁同步电动机；二阶滑模；超螺旋算法；转矩脉动；鲁棒性

永磁同步电动机具有效率高、功率密度大、动态响应快、鲁棒性强、结构简单等优点，在伺服系统中被广泛应用。然而，永磁同步电动机是一个多变量非线性的被控对象，其转速和定子电流之间存在耦合，加之负载的变化等外部扰动的影响，使高性能电动机的控制成为难题[1]。

直接转矩控制(DTC)是继矢量控制之后出现的一种交流电动机调速控制方案,直接转矩控制与矢量控制不同,它是直接将定子磁链和转矩作为控制变量,无需进行磁场定向、矢量变换和电流控制，具有结构简单、动态响应好等优点[2]。但DTC控制存在转矩和磁链脉动较大，损耗增加等问题[3]。虽然通过增加零矢量可以抑制脉动，但是由于可供选择的电压矢量有限，导致无法从根本上消除脉动[4]。文献[5—8]引进电压空间矢量调制(space vector pulse width modulation，SVPWM)方案，其基本思想是，在一个周期内安排多个空间矢量合成所需电压空间矢量。与传统的正弦脉宽调制(space vector pulse width modulation，SPWM)技术相比，SVPWM具有开关损耗小、直流电压利用率高等优点，对转矩和磁链的控制更准确，在一定程度上解决了因电压矢量有限导致的脉动问题[9]。

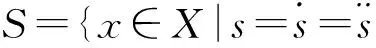
1 超螺旋滑模控制(STSM)

不失一般性，考虑单输入非线性系统：

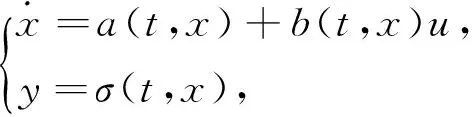
(1)

式中，x∈χ⊂Rn为状态变量，|xi|≤ximax，1≤i≤n；u∈U为控制输入，|u|≤umax；σ(t,x)为输出函数，称为滑模变量，a(t,x)、b(t,x)是光滑的不确定函数。控制目标是使系统在有限的时间内到达滑模面σ(t,x)=0，并具有二阶滑模动态[18]。对滑模变量进行连续求导，可得：

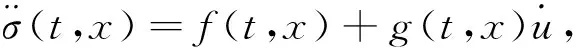
(2)

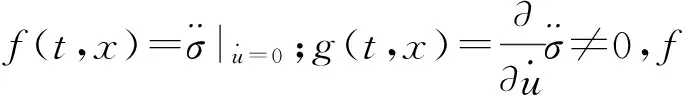
(3)

假设式(3)在全局范围内均成立，则式(2)和式(3)意味着微分包含：

(4)

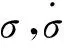
因此，问题转化为寻找一个反馈：

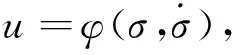
(5)

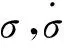
在二阶滑模控制律设计中，存在一种不需要滑模变量导数符号的算法，它能使系统运动轨迹在有限时间内围绕原点螺旋式地收敛到原点，因此被称为超螺旋算法[19-21]。

超螺旋控制算法的控制律设计如式(6)所示：

(6)

式中，KP和KI为正增益，取值范围由式(7)来确定。

(7)

若系统(1)满足式(3)，且式(6)满足式(7)条件，可使STSM控制结构在有限时间内收敛。

2 超螺旋滑模直接转矩控制 (STSM-DTC) 原理

三相永磁同步电动机数学模型为

(8)

式中:ψs=ψsd+jψsq为定子磁链，is=id+jiq为定子电流，Rs为定子电阻，us=usd+jusq为定子电压，ω为转子速度，J为转动惯量，B为摩擦系数，TL为负载转矩，ψf为永磁体磁链，Ls=Ld=Lq，Te为电磁转矩，p为电动机极对数。

根据定子磁链矢量参考系可知，ψs=ψsd，磁链幅值连续求导得：

(9)

式中，Rs,Ls,id,p,ω均为有限的数值，因此式(9)满足式(3)。

STSM磁链控制器设计如下:

(10)

(11)

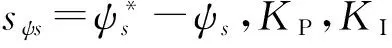
同样对电磁转矩进行连续求导，可得：

(12)

分析方法如定子磁链，KP，KI的范围同样需要稳定条件(7)来确定。

STSM转矩控制器设计如式(13)和式(14)所示:

(13)

(14)

根据式(10)、式(11)和式(13)、式(14)，STSM控制器设计框图如图1所示。

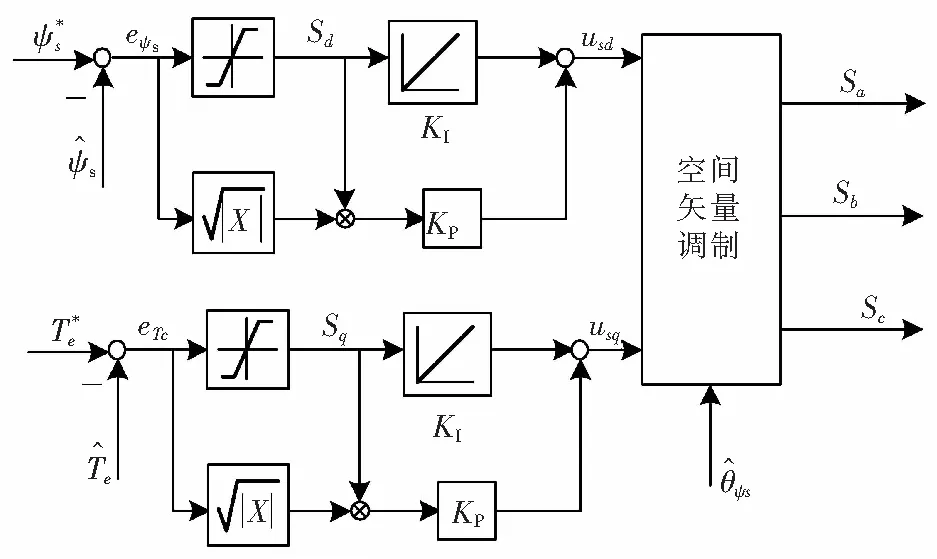
图1 STSM控制器设计框图Fig.1 STSM controller design

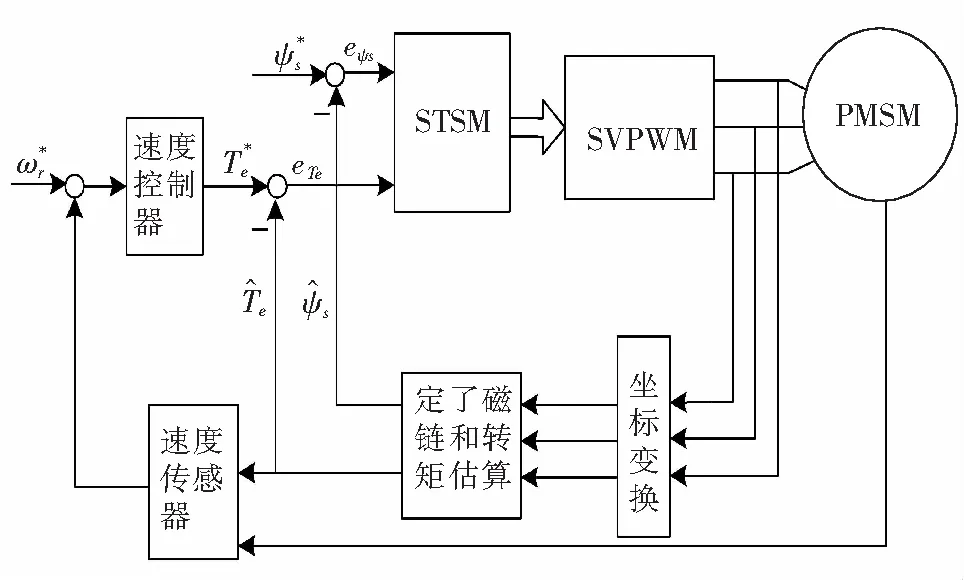
图2 STSM-DTC系统框图Fig.2 STSM-DTC system block diagram

3 仿真结果与分析

为进一步研究STSM-DTC系统的运行性能，将传统的DTC与STSM-DTC 进行仿真比较研究，采用相同的采样时间和仿真步长，分别给定转速nN=100 r/min和nN=600 r/min进行实验。

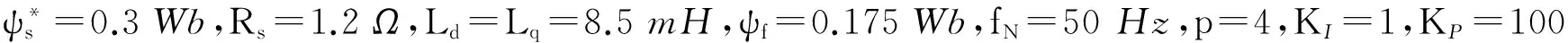
当低速运行nN=100 r/min时，传统DTC和STSM-DTC转矩响应曲线如图3所示。为了使结果更为清晰，对曲线做了局部放大处理，如图3右上角所示。在图4—图6中也作了相应处理。

图3 低速运行情况下转矩响应曲线Fig.3 Torque response at low speed operation

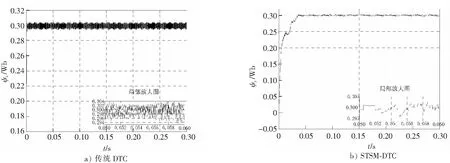
图4 低速运行情况下定子磁链响应曲线Fig.4 Stator flux linkage response curve at low speed operation

由图3可知，传统DTC转矩响应幅值在0.5～1.5N·m之间波动，而STSM-DTC转矩响应幅值在0.8～1.2N·m之间波动，转矩脉动明显减小。

当低速运行nN=100r/min时，传统DTC和STSM-DTC的定子磁链响应如图4所示。

图4定子磁链响应曲线分析情况与图3相同。传统DTC磁链响应曲线幅值在0.294～0.304Wb之间，且波动频率高；而STSM-DTC响应曲线幅值为0.295～0.301Wb，且波动频率明显减小。因此，本文改进方法在电动机低速运行情况下对减小脉动有效，并且获得了良好的动态和静态性能。

当电动机高速运行nN=600r/min时，传统DTC和STSM-DTC转矩响应曲线如图5所示。

图5 高速运行情况下转矩响应曲线Fig.5 Torque response curve at high speed operation

由图5可以看出，当电动机高速运行时，传统DTC转矩响应幅值在0.5～1.5N·m之间波动，而STSM-DTC转矩响应幅值在0.9～1.1N·m之间波动，转矩脉动明显减小。整体仿真过程表明，STSM-DTC系统动态性能更好。

当高速运行nN=600r/min时，传统DTC和STSM-DTC的定子磁链响应曲线如图6所示。

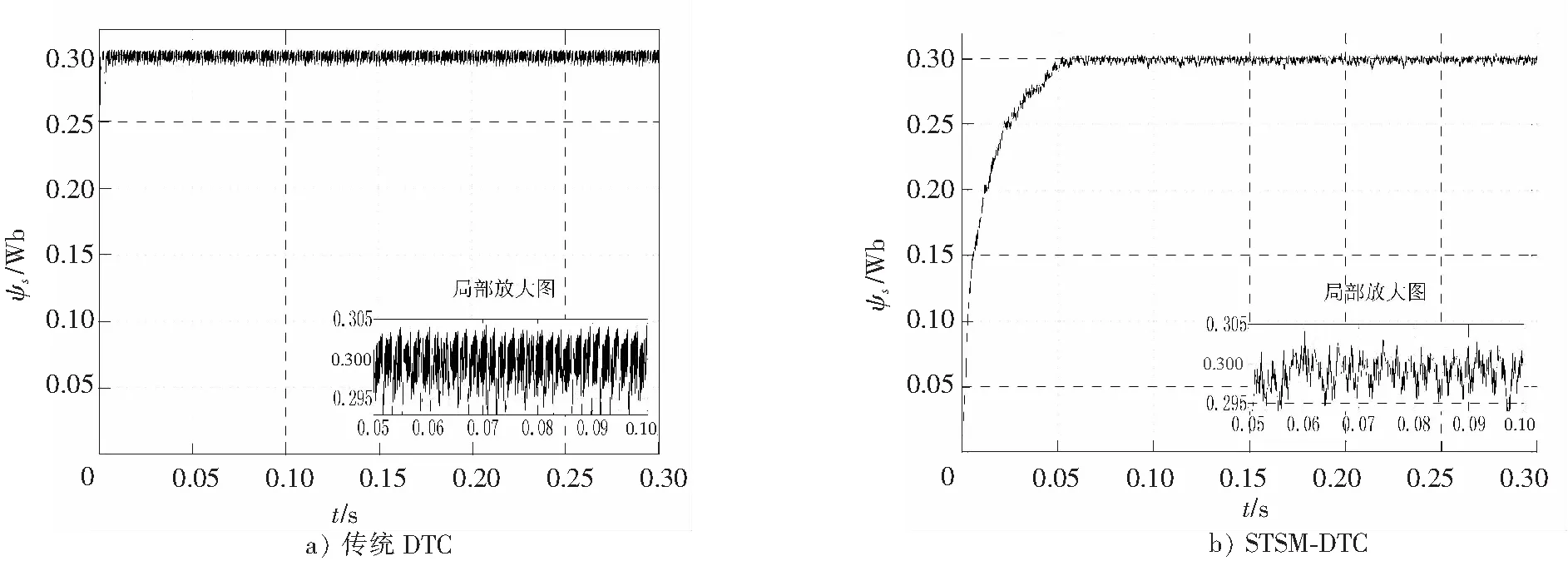
图6 高速运行下定子磁链响应曲线Fig.6 Stator flux linkage response curve at high speed operation

图6定子磁链响应结果分析与图5相同。传统DTC磁链响应曲线幅值在0.295～0.305Wb之间，且波动频率高；而STSM-DTC响应曲线幅值为0.295～0.302Wb，且波动频率明显减小。因此，本文改进方法在电动机高速运行时对减小脉动同样有效。

综合图3—图6可见，无论是高速运行还是低速运行，与传统DTC比较，STSM-DTC系统不仅转矩和磁链脉动均有明显减小，而且动态性能有所提升。

为了研究负载扰动对系统鲁棒性的影响效果，在0.15s时， 转矩给定由1N·m突变为3N·m，转矩变化曲线如图7所示。

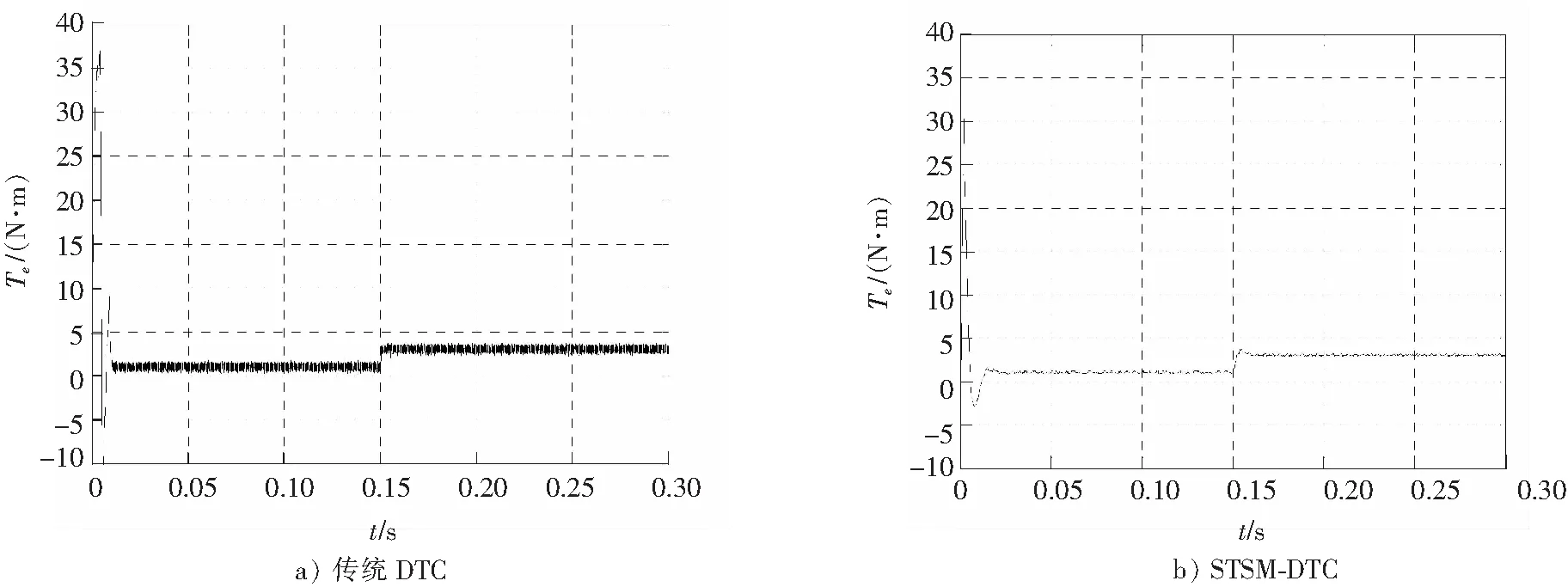
图7 负载突变转矩响应曲线Fig.7 Load torque mutation response curve

由图7可知，本文所采用的超螺旋二阶滑模控制策略系统对负载干扰和系统参数变化的鲁棒性更强，当外部有扰动存在时，系统能够在更短的时间内恢复稳定，无偏差地跟踪给定值，且超调量很小。参数变化对控制系统扰动的分析机理与负载扰动分析机理相同。

综上所述，STSM-DTC与传统的DTC比较，能够更精确地跟踪给定信号，转矩、磁链脉动明显减小，在转矩突变的情况下能够快速收敛，具有很好的鲁棒性，提高了系统的整体性能。

4 结 语

本文在永磁同步电动机数学模型和直接转矩控制的基础上，采用超螺旋结构设计了二阶滑模控制器，取代传统控制直接转矩控制中的PI控制器，并利用Matlab/Simulink进行仿真研究及分析。仿真结果表明，与传统直接转矩控制相比，在有限的时间里能够快速精准地跟踪速度给定，对转矩突变表现出很强的鲁棒性，转矩脉动小，提高了系统的稳定性。但是，定子磁链响应曲线的上升段还有欠缺，其主要原因是定子电阻变化的累计误差。若想进一步提高系统的控制性能，需要减小定子电阻对定子磁链估算带来的影响。

/references：

[1] 张冀，张兴华. 永磁同步电动机二阶滑模控制[J]. 微电动机,2010,43(5):62-65. ZHANG Ji, ZHANG Xinghua. Second order sliding mode control of permanent magnet synchronous motor[J]. Micromotors,2010, 43(5):62-65.

[2] 赵利. 同步电动机励磁电流计算与用电系统功率因数提高[J]. 河北工业科技,2011,28(1):26-29. ZHAO Li. Excitation current calculation of synchronous motors and power factor improvement of power system[J]. Hebei Journal of Industrial Science and Technology, 2011,28(1):26-29.

[3] 刘英培. PMSM直接转矩控制方法及实验研究[D].天津：天津大学,2010. LIU Yingpei. Research on Direct Torque Control Methods and Experiment of PMSM[D]. Tianjin:Tianjin University, 2010.

[4] 贾洪平,贺益康.永磁同步电动机直接转矩控制中零矢量的作用研究[J]. 电气传动，2006，36(4):13-16. JIA Hongping, HE Yikang. Study on null vector in a direct torque controlled permanent magnet synchronous motor[J]. Electric Drive, 2006, 36(4):13-16.

[5] LASCU C, BOLDEA I, BLAABJERG F.A modified direct torque control for induction motor sensorless drive[J]. IEEE Trans Industry Applic, 2000,36(1):122-130.

[6] LAI Y S, WANG W K, CHEN Y C.Novel switching techniques for reducing the speed ripple of ac drives with direct torque control[J]. IEEE Trans Industrial Electronics, 2004,51(4):768-775.

[7] 范心明. 基于SIMULINK的SVPWM仿真[J].电气传动自动化,2009,31(3):19-21. FAN Xinming. Simulation of SVPWM based on SIMULINK[J]. Electric Drive Automation, 2009, 31(3)：19-21.

[8] 史晓永,王步来,陈雪琴,等.基于SVPWM的永磁同步电动机直接转矩控制系统的建模与仿真[J].通信电源技术,2014,31(3):25-26. SHI Xiaoyong, WANG Bulai, CHEN Xueqin, et al. Modeling and simulation of PMSM direct torque control system based on the SVPWM[J]. Telecom Power Technology, 2014,31(3):25-26.

[9] 高键,姜星星. 基于SVM的永磁同步电动机直接转矩控制的仿真研究[J]. 科学技术与工程,2013,13(1):63-69. GAO Jian, JIANG Xingxing. Simulation research on direct torque control of permanent magnet synchronous motor based on SVM[J]. Science Technology and Engineering, 2013，13(1):63-69.

[10] 张袅娜,许祥军,林晓梅. 基于二阶滑模的永磁同步电动机直接转矩控制[J]. 微电动机，2010,43(10):33-35. ZHANG Niaona, XU Xiangjun, LIN Xiaomei. Direct torque control of permanent magnet synchronous motor based on two order sliding mode[J]. Micromotors, 2010,43(10):33-35.

[11] 袁赣南,左志丹,曲桂婷,等. 二阶滑模变结构控制系统的滑模到达条件[J]. 华中科技大学学报(自然科学版)，2013,41(6):70-75. YUAN Gannan, ZUO Zhidan, QU Guiting, et al. Reaching condition of sliding mode in second-order sliding mode variable structure control systems[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2013,41(6):70-75.

[12] 李琳. 滑模变结构控制系统抖振抑制方法的研究[D]. 大连：大连理工大学,2006. LI Lin. A Study of Chattering Elimination in Sliding Mode Control System[D]. Dalian：Dalian University of Technology, 2006.

[13] 孙宜标,魏秋瑾,王成元. 永磁直线同步电动机二阶滑模控制仿真研究[J]. 系统仿真学报,2009,21(7):2037-2040. SUN Yibiao, WEI Qiujin, WANG Chengyuan. Simulation research of second order sliding mode control for permanent-magnet linear synchronous motor[J]. Journal of System Simulation, 2009, 21(7):2037-2040.

[14] 张苏英,李林静,刘慧贤,等. 基于滑模自适应的永磁同步电动机无传感器控制[J]. 河北科技大学学报,2016,37(4):382-389. ZHANG Suying,LI Linjing,LIU Huixian, et al. Sensorless control of permanent magnet synchronous motor based on sliding mode adaptive system[J]. Journal of Hebei University of Science and Technology, 2016,37(4):382-389.

[15] LEVANT A.Higher-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2010, 76(9):924-941.

[16] LEVANT A.Principles of 2-sliding mode design[J]. Automatica, 2007, 43(4):576-586.

[17] 杨兴明,高银平. 不确定欠驱动系统的高阶自适应Super-Twisting滑模控制[J]. 模式识别与人工智能,2014,27(9):808-814. YANG Xingming, GAO Yinping. High-order adaptive Super-Twisting sliding mode control for uncertain underactuated systems[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(9):808-814.

[18] CHAI Huawei. Sliding mode control of PMSM based on robust differentiator[C]// Proceedings of 2010 Second International Conference on Computational Intelligence and Natural Computing(CINC 2010).[S.l.]:[s.n.],2010:37-40.

[19] 周宇友. 基于二阶滑模的发动机转速控制研究[D]. 南京：南京理工大学,2012.

[20] 杨雪. 永磁直线同步电动机的二阶滑模控制[D]. 沈阳：沈阳工业大学,2007. YANG Xue. The Second Order Sliding Mode Control of Permanent Magnet Linear Synchronous Motor[D]. Shenyang: Shenyang University of Technology,2007.

[21] LASCU C, BLAABJERG F.Super-twisting sliding mode direct torque control of induction machine drives[J]. Energy Conversion Congress and Exposition, 2014:5116-5122.

Research of PMSM-DTC system based on the super-twisting second sliding mode control

ZHANG Suying, MA Heming, MO Zhaojin, LI Linjing, LIU Huixian

(School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China)

Aiming at the problems that the conventional permanent magnet synchronous motor direct torque control system (PMSM-DTC) is susceptible to the influence of parameter change and torque ripple, it is proposed that the space voltage vector modulation technique (SVPWM) is used instead of the traditional sinusoidal pulse width modulation (SPWM), on the basis of which the second-order sliding mode variable structure control rate with super-twising algorithm is introduced, with the stator flux linkage and torque as the controlled object to design the controller instead of traditional PI controller in the system. The simulation results show that the strategy not only eliminates effectively the first-order sliding mode chattering problems, significantly reducing the stator flux linkage and torque ripple, but also has strong ability of speed tracking, with robustness to load disturbance, and parameter changes, etc., therefore can be well applied in motor control.

robust control; PMSM; second order sliding mode; super-twisting sliding mode algorithm; torque ripple; robustness

1008-1542(2017)02-0176-07

10.7535/hbkd.2017yx02012

2016-04-08；

2016-09-08；责任编辑：李 穆

河北省自然科学基金(F2014208148)

张苏英(1961—)，女，河北深州人，教授，主要从事复杂系统理论及应用方面的研究。

马贺明。E-mail:917496038@qq.com

TP27;TP351

A

张苏英,马贺明,墨昭瑾，等.基于超螺旋二阶滑模的PMSM-DTC系统研究[J].河北科技大学学报,2017,38(2):176-182.

ZHANG Suying, MA Heming, MO Zhaojin,et al.Research of PMSM-DTC system based on the super-twisting second sliding mode control[J].Journal of Hebei University of Science and Technology,2017,38(2):176-182.