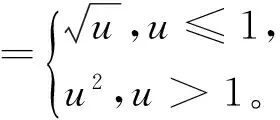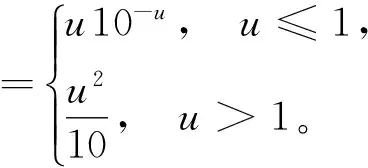一类弹性梁方程正解的存在性
2017-04-14鞠梦兰王文霞郝彩云
鞠梦兰,王文霞,郝彩云
(太原师范学院数学系,山西晋中 030619)
一类弹性梁方程正解的存在性
鞠梦兰,王文霞,郝彩云
(太原师范学院数学系,山西晋中 030619)
弹性梁是弹力力学和工程物理中一种比较常见的数学模型,为了将此模型更准确地应用于工程领域中,在对一端固定,一端滑动支撑的弹性梁方程研究的基础上,研究了此类弹性梁方程的多解性。通过将此类边值问题转化为积分方程后,进而等价于算子的不动点问题,结合其Green函数的性质与Guo-Krasnoselskii锥拉伸与压缩不动点定理,讨论了此类弹性梁方程正解的存在性问题。在非线性项满足适当条件下建立参数的取值范围,获得了此类边值问题至少有1个正解,2个正解的存在性结果与正解的不存在性结果。结论上获得了关于此类问题至少有1个正解,2个正解及没有正解的存在的特征值区间。研究结果有助于弹性梁的稳定性分析,丰富了材料力学的相关理论。
非线性泛函分析;弹性梁;正解;Guo-Krasnoselskii不动点定理;材料力学
考察边值问题:
(1)
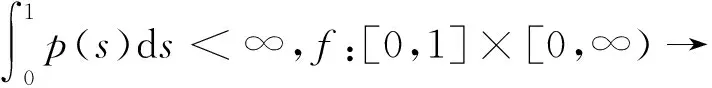
不同的梁方程可以通过不同边界条件的四阶边值问题来刻画,由于梁方程的实际背景及意义,近年来对四阶边值问题的研究很活跃,尤其是对两端简单支撑与两端固定的梁方程(即边界条件为u(0)=u(1)=u″(0)=u″(1)和u(0)=u(1)=u′(0)=u′(1)=0)的研究,并且取得了丰硕的研究成果[1-11];也有不少研究者致力于对悬臂梁方程(即边界条件为u(0)=u′(0)=u″(1)=u‴(1)=0)的研究[12-13]。目前对一端固定,一端滑动支撑的梁方程(即本文所讨论情形)的讨论还比较少见。陆海霞等[14]应用锥理论和不动点指数方法研究了此类梁方程至少有1个正解的存在性问题。 受此启发,文献[15]研究了此类梁方程的特征值问题,获得了至少有1个正解存在的特征区间。但是此类问题的多解性研究尚不多见,通过对三阶边值问题多解性文献的研读发现[16-19],研究者们通常利用Guo-Krasnoselskii锥拉伸与压缩不动点定理,单调迭代技术去讨论这类问题的多解性问题。本文主要通过建立适当的锥,利用锥上的Guo-Krasnoselskii锥拉伸与压缩不动点定理,建立了特征值问题(1)至少有1个,2个及没有正解的存在的特征区间。
1 预备和记号
引理1 设
(2)
则G(t,s)是边值问题:
(3)
的格林函数。
引理2[15]1)G(t,s)≥0,(t,s)∈[0,1]×[0,1];
2)G(t,s)>0,(t,s)∈(0,1)×(0,1);
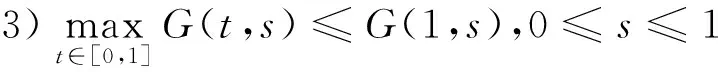

下面给出一些记号:

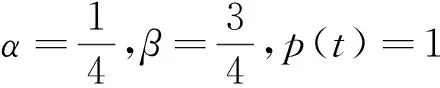

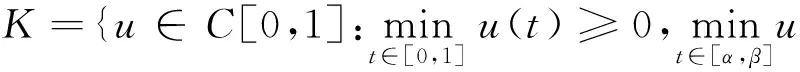
Kc={u∈K,‖u‖≤c}, ∂Kc={u∈K,‖u‖=c},
引理3Tλ是K→K全连续算子。
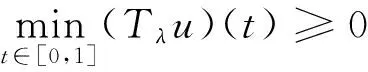
另一方面,
τ‖Tλu‖,
即Tλ(K)⊂K,由f与p的连续性易得Tλ的连续性。
下证Tλ是紧的。
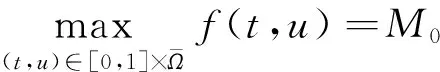
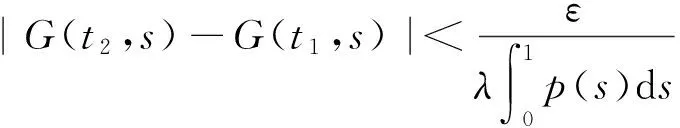


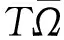
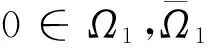
1)‖Tu‖≤‖u‖,u∈K∩∂Ω1且‖Tu‖≥‖u‖,u∈K∩∂Ω2;
2)‖Tu‖≥‖u‖,u∈K∩∂Ω1且‖Tu‖≤‖u‖,u∈K∩∂Ω2;
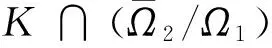
引理4 设存在c1,c2>0,且c1≠c2,使得:

(4)
则BVP(1)至少有1个正解。

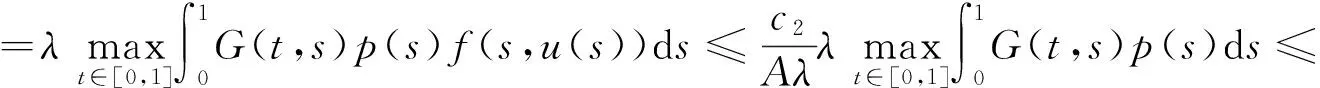
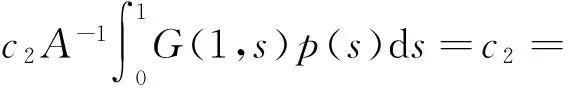
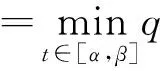
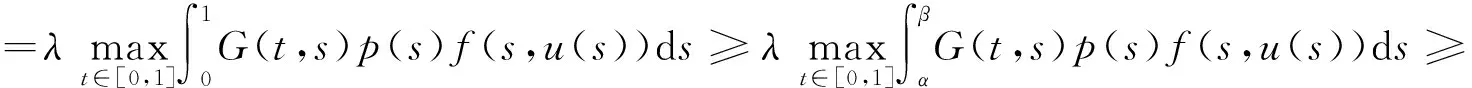
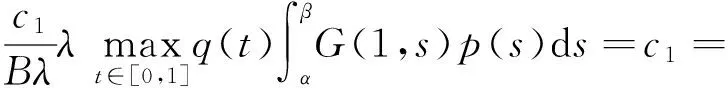
由定理1可知,存在u*∈K使得Tλu*=u*,且c1≤‖u*‖≤c2。由于p(s)f(s,0)>0,G(t,s)>0,t,s∈(0,1),得u*(t)=(Tλu*)(t)>0,t∈(0,1),从而u*(t)是BVP(1)的正解。
2 主要结论
记:
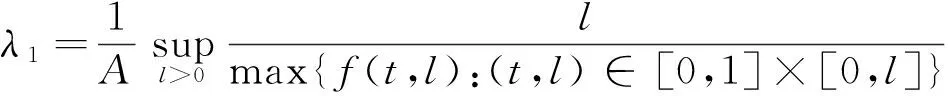

定理2 若λ2<λ1,则对任意的λ∈(λ2,λ1),BVP(1)至少有1个正解。
证明 由λ∈(λ2,λ1),则存在0 需要证明a≠b。若不然,即a=b,有: 由A>B且 min{f(t,l):(t,l)∈[α,β]×[τa,a]}≤max{f(t,l)∈[0,1]×[0,a]}, 从而产生矛盾。由引理4知BVP(1)至少有1个正解u1,a≤‖u1‖≤b。 定理3 若f0=f∞=∞,则对任意的λ∈(0,λ1),BVP(1)至少有2个正解。 证明 记: (5) 另一方面,由f0=f∞=∞,存在b1,b2,0 即 这样找到了两对数对{b1,a1},{a2,b2}使得: 由引理4知BVP(1)至少有2个正解u1,u2,b1≤‖u1‖≤a1 定理4 若f0=f∞=0,则对任意的λ∈(λ2,∞),BVP(1)至少有2个正解。 证明 记: (6) 由引理4知BVP(1)至少有2个正解u1,u2,a1≤‖u1‖≤b1 设u∈K是BVP(1)的解,则有: 从而产生矛盾,得证。 设u∈K是BVP(1)的解,则有: 从而产生矛盾,得证。 例1 考虑边值问题: 例2 考虑边值问题: 经计算M=276 480,由定理6知对任意的λ∈(276 480,∞),BVP(1)不存在正解。 /References: [1] BAI Zhanbing, WANG Haiyan. On positive solutions of some nonlinear fourth-order beam equations[J].Journal of Mathematical Analysis Applications & ications, 2002, 270(2):357-368. [2] LIU Yansheng. Multiple positive solutions of nonlinear singular boundary value problem for fourth-order equations[J]. Applied Mathematics Letters, 2004, 17(7): 747-757. [3] 闫东明.一类四阶两点边值问题多个正解的存在性[J].工程数学学报,2010,27(1):133-138. YAN Dongming. Existence of multiple positive solutions for a class of fourth-order two-point boundary value problems[J]. Chinese Journal of Engineering Mathematics, 2010, 27(1): 133-138. [4] 索秀云,郭少聪,张继叶,等.四阶非局部边值问题方程组正解的存在性[J].河北科技大学学报,2012,33(3):197-206. SUO Xiuyun, GUO Shaocong, ZHANG Jiye, et al. Existence of positive solutions for nonlocal fourth order boundary value problem systems[J]. Journal of Hebei University of Science and Technology, 2012, 33(3): 197-206. [5] 杨飞,刘玉敬,郭彦平.含有一阶导数的非局部四阶边值问题正解的存在性[J].河北科技大学学报,2012,33(4):283-289. YANG Fei, LIU Yujing, GUO Yanping. Positive solutions to nonlocal fourth-order boundary value problems with dependence on the first order derivative[J]. Journal of Hebei University of Science and Technology, 2012, 33(4): 283-289. [6] WANG Qi, GUO Yanping, JI Yude. Positive solutions for fourth-order nonlinear differential equation with integral boundary conditions[J].Discrete Dynamics in Nature and Society, 2013(96):292-297. [7] 吴红萍,马如云.一类四阶两点边值问题正解的存在性[J].应用泛函分析学报,2000,2(4):342-348. WU Hongping, MA Ruyun. Positive solutions of fourth-order two-point boundary value problem[J]. Acta Analysis Function Alis Applicata, 2000, 2(4): 342-348. [8] 马如云,吴红萍.一类四阶两点边值问题多个正解的存在性[J].数学物理学报,2002,22A(2):244-249. MA Ruyun, WU Hongping. Positive solutions of fourth-order two-point boundary value problem[J]. Acta Mathematica Scientia, 2002, 22A(2): 244-249. [9] YAO Qingliu. Positive solutions for eigenvalue problems of fourth-order elastic beam equations[J]. Applied Mathematics Letters, 2004, 17(2): 237-243. [10]闫东明.一类四阶两点边值问题正解的存在性[J].应用数学学报,2010,33(6):1113-1122. YAN Dongming.Positive solution for a class of fourth-order two-point boundary value problem[J].Acta Mathematicae Applicatae Sinica, 2010,33(6):1113-1122. [11]ZHAI Chengbo, SONG Ruipeng, HAN Qianqian. The existence and the uniqueness of symmetric positive solutions for a fourth-order boundary value problem[J]. Computers and Mathematics with Applications, 2011, 62(6): 2639-2647. [12]LI Shunyong, ZHANG Xiaoqin. Existence and uniqueness of monotone positive solutions for an elastic beam equation with nonlinear boundary conditions[J]. Computers and Mathematics with Applications, 2012, 63(9): 1355-1360. [13]WANG Wenxia, ZHENG Yanping, YANG Hui, et al. Positive solutions for elastic beam equations with nonlinear boundary conditions and a parameter[J]. Boundary Value Problems,2014, 2014(1): 80. [14]陆海霞,孙经先.一类四阶非线性微分方程两点边值问题的正解[J].数学的实践与认识,2014,44(8):229-235. LU Haixia, SUN Jingxian. Positive solution of two-point boundary value problems for fourth-order nonlinear differential equation[J]. Mathematics in Practice and Theory, 2014, 44(8): 229-235. [15]鞠梦兰,王文霞,郝彩云.一类四阶两点边值问题正解的存在性[J].成都大学学报(自然科学版),2016,35(1):37-40. JU Menglan, WANG Wenxia, HAO Caiyun. Existence of positive solution to fourth-order two-point boundary value problem[J]. Journal of Chengdu University(Natural Science), 2016,35(1): 37-40. [16]葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007. [17]SUN Yongping. Positive solution of singular third-order three-point boundary value problem[J]. Journal of Mathematical Analysis and Applications, 2005, 306(2): 589-603. [18]LI Shuhong. Positive solutions of nonlinear singular third-order two-point boundary value problem[J]. Journal of Mathematical Analysis and Applications,2008, 323(11):413-425. [19]张海娥.带积分边界条件的奇异三阶边值问题的单调正解[J].唐山学院学报,2012,25(6):37-39. ZHANG Haie.Monotone positive solutions for singular third-order BVPs involving integral boundary conditions[J]. Journal of Tangshan College, 2012, 25(6): 37-39. [20]郭大均.非线性泛函分析[M].第2版.济南:山东科学技术出版社,2001. Existence of positive solutions to a class of elastic beam equations JU Menglan, WANG Wenxia, HAO Caiyun (Department of Mathematics, Taiyuan Normal University, Jinzhong, Shanxi 030619, China) Elastic beam is a kind of mathematical model in elastic mechanics and engineering physics. For now, this type of model is often used in real life. On the basis of the relative research on the elastic beam equations with one end fixed and one end sliding support, and the multiple solutions of the elastic beam equation are researched. In this paper, through putting this problem into an integral equation, which is equivalent to an operator fixed-point problem, and combining with the properties of Green function and Guo- Krasnoselskii fixed point theorem of cone expansion and compression, the existence of positive solutions of this kind of elastic beam equations is discussed. Under various assumptions on nonlinear terms, the intervals of the parameters are established, and the existence of one positive solution, two positive solutions or nonexistence of positive solutions for this elastic beam equations are obtained. In conclusion, the intervals of eigenvalue about this problem for at least one positive solution, two positive solutions and nonexistence of positive solutions are obtained. The study of the existence of such solution can not only contribute to the stability analysis of elastic beams, but also enrich the theory of material mechanics. nonlinear functional analysis theory; elastic beam; positive solution; Guo-Krasnoselskii fixed-point theorem; material mechanics 1008-1542(2017)02-0131-06 10.7535/hbkd.2017yx02005 2016-05-16; 2016-12-28;责任编辑:张 军 国家自然科学基金(11361047) 鞠梦兰(1991—),女,重庆人,硕士研究生,主要从事非线性算子方面的研究。 王文霞教授。E-mail:wwxgg@126.com O175.8 MSC(2010)主题分类:34B05 A 鞠梦兰,王文霞,郝彩云.一类弹性梁方程正解的存在性[J].河北科技大学学报,2017,38(2):131-136. JU Menglan,WANG Wenxia,HAO Caiyun.Existence of positive solutions to a class of elastic beam equations[J].Journal of Hebei University of Science and Technology,2017,38(2):131-136.
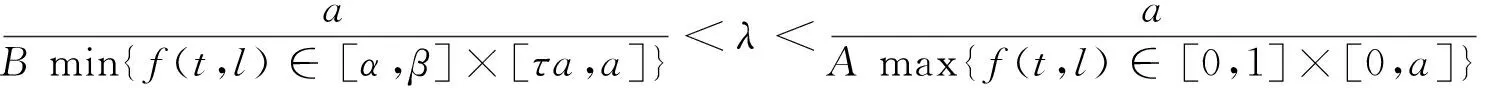



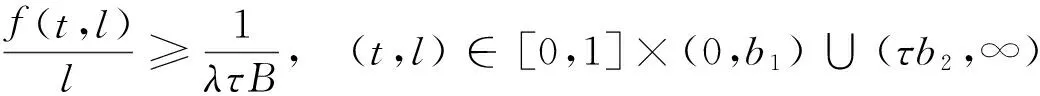
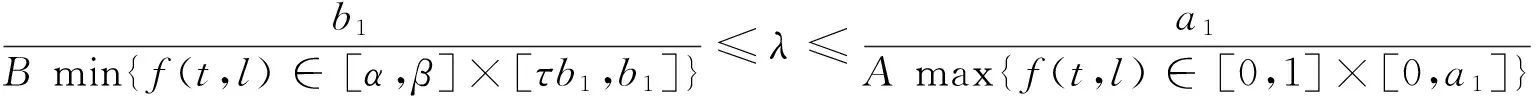
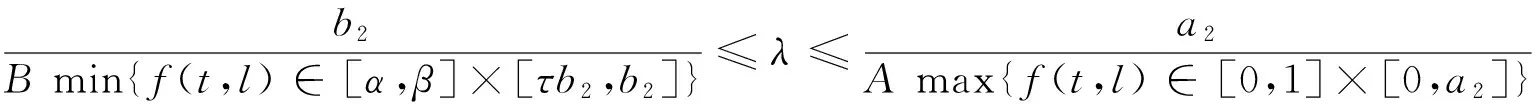
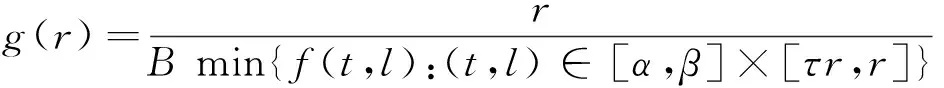
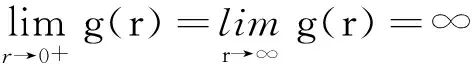

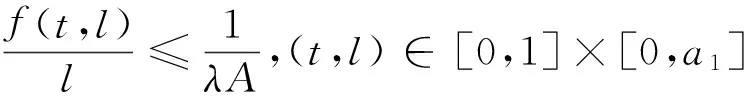
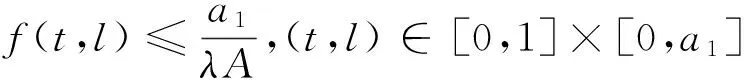


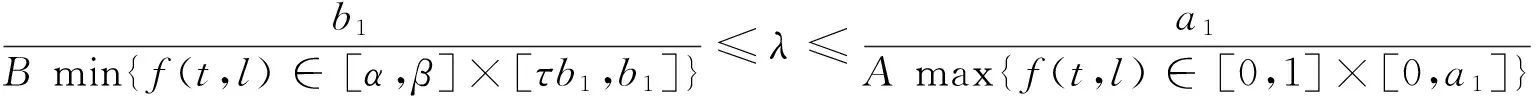
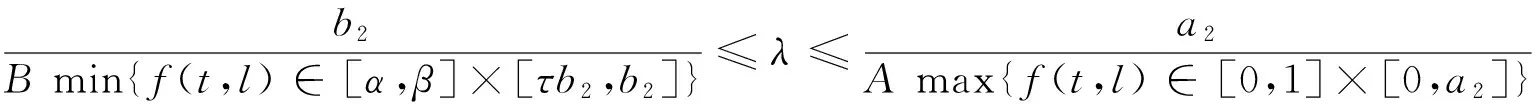
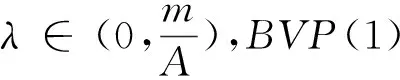
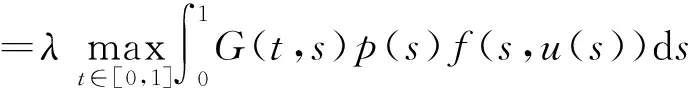
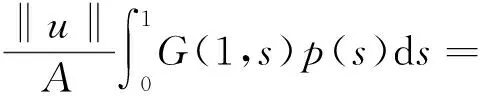
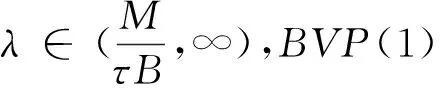

3 例子