有向网络下的CoDA社区发现算法评估

郭 松，张冬雯，许云峰，杨玉林，郑雅洁，柳晨光

(河北科技大学信息科学与工程学院，河北石家庄 050018)

有向网络下的CoDA社区发现算法评估

郭 松，张冬雯，许云峰，杨玉林，郑雅洁，柳晨光

(河北科技大学信息科学与工程学院，河北石家庄 050018)

CoDA算法是一种基于概率模型的能识别二分结构的社区发现算法。为了验证该算法的社区划分效果，采用信息检索领域的F-measure标准，对有向网络下重叠社区和非重叠社区的CoDA社区发现算法进行评估。F-measure标准中F1-measure值的大小能反映CoDA算法社区划分效果的优劣。实验所用的数据集由LFR Benchmark工具生成，数据集中节点数最小为100，最大为20 000，每增加100节点对CoDA算法社区划分效果评估一次。分析实验结果可以得出，当节点数小于1 600时，CoDA算法的划分效果较好。当节点数大于1 600时，随着节点个数增多，CoDA算法社区划分效果逐渐变差。由此说明，基于概率模型的CoDA算法适用于小规模社交网络社区的划分。

算法理论；社区发现；CoDA算法；有向网络；评估；F-measure

社区发现是在给定网络中，将物理对象或抽象对象的集合分组为类似对象组成的多个社区。社区发现可以应用在许多领域，例如，在商业领域，社区发现可以用于对不同的客户群分组，寻找潜在市场；在生物领域，社区发现可以用于对动植物分类和对基因分类，获取对种群固有结构的认识；在因特网领域，社区发现可以用来在网上进行文档归类，修正错误信息；在保险领域，社区发现可以用来对保险单持有者的分组识别汽车保险欺诈等。因此，社区发现算法在现实生活中有着广泛的应用。

目前，许多学者从事社区发现研究，由于他们对节点集或者边集进行划分时采取了不同标准，提出了多种多样的社区发现算法。无向网络中的社区发现算法分为图论分区法[1-4]、链接分区法[5-7]、局部扩张和优化分区法[8-10]、模糊划分法[11-13]和基于代理的分区法[14-15]5类。随着无向网络中社区发现算法的逐渐成熟，一些学者尝试将无向网络社区发现算法扩展到有向网络，以期利用已有的方法解决新问题。例如，无向网络中的DOCNet算法采用聚集系数计算节点的重要性，FAGIOLO[16]改进了DOCNet算法，并将其扩展到有向网络中。NEWMAN 等[1]在无向网络中建立了模块度优化算法——谱二分法，然后将其扩展到有向网络中，并提出有向网络中模块度的概念。NICOSIA 等[17]将有向网络中模块度概念进行了扩展，并将重叠社区考虑在内。

随着社区发现算法的不断增多，如何衡量算法的优劣成为了一个重要的问题，因此，对社区发现算法的评估也成为了研究者关注的问题。目前常用的社区发现算法评估方法可分为外部评估法和内部评估法两大类。外部评估法是基于一种预先指定的结构，反映了人们对数据集社区结构的直观认识，主要包括正确率(Accuracy)[18]、Rand系数(Rand Index)[19]、Jaccard系数(Jaccard Index)[20]等指标。内部评估法是利用未知社区结构固有特征和量值来评估一个社区发现算法的社区划分效果，主要包括模块度(Modularity)[1]和Coverage[21]等指标。

CoDA(communities through directed affiliations)社区发现算法[22]是一个新的社区发现算法，它能对一种新型的网络结构进行社区划分。本文主要用F-measure标准对CoDA社区发现算法进行详细评估，以分析CoDA算法在不同节点数据集下社区划分结果的变化规律。

1 CoDA社区发现算法的概述及实现

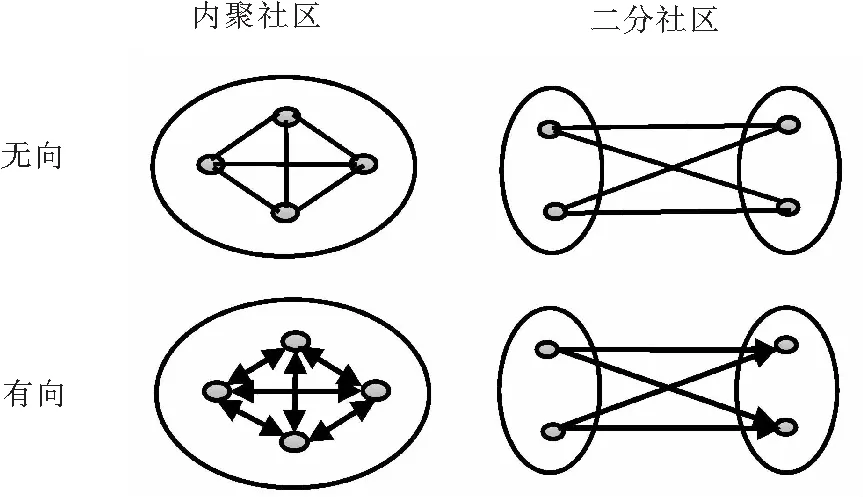
图1 两种类型的网络和两种类型的社区结构Fig.1 Two types of networks and two types of community structures

CoDA社区发现算法是由斯坦福大学的Jaewon Yang等提出的，该算法引起关注的原因是它对社区结构提出了一个更加新颖、全面的定义：有相似的连接模式的节点，即便它们不相连也可以组成一个社区。新的社区结构的概念源于结构对等的社会网络文化，这一文化是指具有社会同质性的节点不仅包括能连接到彼此的节点(即内部组连接)，还包括以适当方式连接到网络中其他部分的节点(外部连接)。图1表示出了两种不同的社区概念。其中传统的内聚社区由社区内部链接占据主导地位，且其内部节点以双向边形式链接；而二分社区由社区间的单向链接占据主导地位。

CoDA社区发现算法在两方面较为先进：第一，该算法不仅可以发现内聚社区还可以成功地发现二分社区；第二，该算法可以成功发现有向网络中的重叠社区。

设B(V,C,M)是一个二分图。其中V是节点集，C是社区集，M是将V和C连接在一起的边集。该模型可以通过概率p(u,v)生成从节点u∈V到节点v∈V的有向边，生成一个有向图G(V,E)，其中E为边的集合:

(1)

通过将有向关系网络模型拟合到G(V,E)识别社区，即，使用最大似然法找到关系图B和所有社区c∈C的概率集合{Pc}。

(2)

取对数得：

(3)

引入变量Muc和Lvc表示节点成员资格。用Muc表示节点u是否具有社区c的链出成员资格，取值为0或者1；Lvc表示节点v是否具有社区c的链入成员资格，取值为0或者1。因此，式(1)可以表示为

(4)

其中Cuv={c|(u,c),(c,v)∈M}，如果Cuv=∅，则基础边缘概率为p(u,v)=1/|V|。

(1-pc)MucLvc表示只有当节点u有社区c的链出成员资格，节点v有社区c的链入成员资格时取值为(1-pc)，否则为1。则∏c(1-pc)MucLvc只要其中一个社区c0使Muc0Lvc0=1，则∏c(1-pc)MucLvc≠1，则p(u,v)≠0。只要存在一个社区c0，节点u有其链入成员资格，节点v有其链出成员资格，就有可能存在有向边〈u,v〉,且其概率可用式(4) 表示。

令1-pc=exp(-ac)，其中ac≥0。代入式(4)得，

(5)

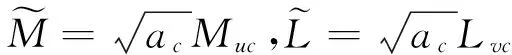
(6)

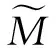
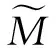
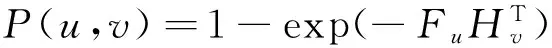
(7)

式(3)可转化为连续优化问题：

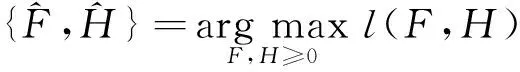
(8)

其中

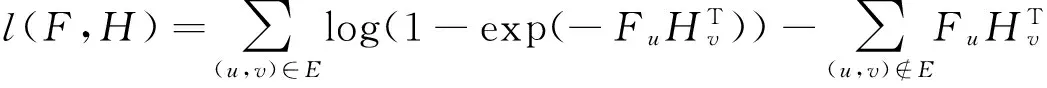
(9)

使用最大似然法求出l(F,H)=logP(G|F,H)，取得最大值时的非负关系矩阵，来拟合有向关系网络模型，以达到社区划分的目的。

2 评估方法

评估方法借鉴了信息检索领域中的F-measure标准[23]。F-measure包含准确率和召回率两方面。其中准确率是检索出相关文档数与检索出的文档数的比率，衡量系统的查准率；召回率是指检索出的相关文档数和文档库中所有相关文档数的比率，衡量系统的查全率。本文将F-measure标准中的文档数替换为节点对个数，进而将F-measure标准应用到社区发现算法的评估领域。F-measure可以很好地刻画某社区发现算法对社交网络的社区划分结果与标准数据集中社区划分结果的差异，在此用F-measure标准对CoDA社区发现算法进行评估。

社区中节点对的归属情况见表1。其中：a表示原始数据集中属于同一个真实社区，社区划分后也属于同一个社区中的节点对数目；b表示原始数据集中不属于同一个真实社区，社区划分后却划分到同一个社区中的节点对数目；c表示原始数据集中属于同一个真实社区，社区划分后却没被划分到同一个社区中的节点

表1 社区划分结果

对数目；d表示原始数据集中即不属于同一个真实社区，社区划分后也不属于同一个社区中的节点对数目。

准确率(Precision)是输出结果中被划分到同一社区的2个节点组成的节点对在数据集中属于同一真实社区的比例，计算公式如式(10)所示：

(10)

召回率(Recall)是输出结果中被划分到同一社区中的2个节点且在数据集中属于同一真实社区的节点对占划分结果中社区内所有节点对的比例，计算公式如式(11)所示：

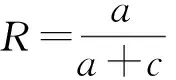
(11)

准确率与召回率都只能反映算法单方面的性质，且这2个参数往往有相反的变化趋势，而F1-measure 将准确率与召回率进行综合考虑，能够反映算法的综合性能。其定义如式(12)所示:

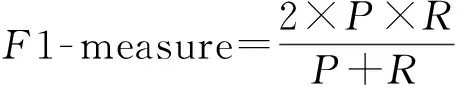
(12)

2.1 评估程序流程图

图2 评估程序流程图Fig.2 Flow chart of evaluation procedure

评估程序流程图如图2所示，本程序采用Java语言实现。该评估方法为外部评估法，其特点是标准社区结构已知。首先，读取数据集中的标准社区结构文件，得到标准社区结构中社区编号与其包含节点的对应关系HashMap〈String, LinkedList〈String〉〉communities。其次，根据得到的标准社区情况communities分社区遍历，构造标准社区中的节点对HashSet〈String〉nodePairInReal。然后，读取被某算法处理后的社区情况，构造处理后社区中的节点对nodePairInBack，在此过程中判断每个节点是否包含在真实社区的节点对 nodePairInReal之中，如果存在，则构造既包含在真实社区中又在某算法处理后的社区中的节点对nodePairCorrect，同时，将此节点从nodePairInReal中移除。其中节点对指位于同一社区中的2个节点的组合。其中nodePairCorrect对应表1中a，nodePairInBack对应表1中b，nodePairInReal对应表1中c。最后根据式(10)—式(12)依次计算出准确率、召回率和 F1-measure的值。

2.2 有向网络下重叠社区CoDA算法的评估

实验所用有向网络下重叠社区的标准数据集由LFRBenchmark[24]生成。数据集中节点平均度数为 10，最大度数为50，混合参数为0.2，社区最小尺寸为20，最大尺寸为100，40%的重叠节点，且每个重叠节点同时属于 4 个社区。节点数从100 到20 000，每100个节点进行一次测试。评估结果如图3和图4所示。其中图3表示链入成员的评估结果，图4表示链出成员的评估结果。

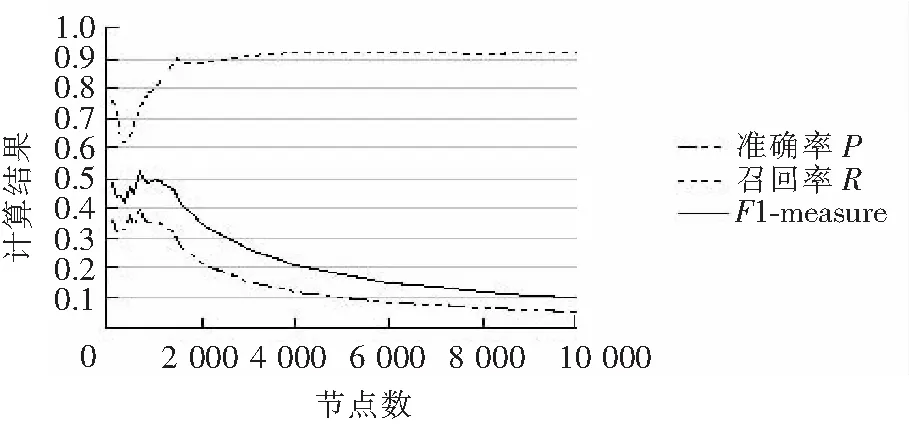
图3 链入成员评估结果图Fig.3 Evaluation result of incoming members

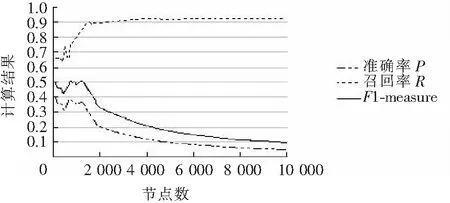
图4 链出成员评估结果图Fig.4 Evaluation result of outgoing members

通过实验结果可以发现，在有向网络带重叠社区的情况下，相同节点数据集的链入成员资格和链出成员资格之间的准确率、召回率和F1-measure几乎相等。数据集节点数在1 600以内时，CoDA社区发现算法的社区划分效果比较好，F1-measure在0.4以上。链入成员在节点为700时CoDA社区划分效果最好，此时F1-measure达到0.524；链出成员在节点为1 200时CoDA社区划分效果最好，此时F1-measure达到0.506。当数据集节点数超过1 700时，随着节点的不断增多，召回率不断升高，且趋近于1；但是准确率不断下降，且趋近于0.1；F1-measure呈明显下降趋势，其值趋近与0.1。当节点数超过10 000时，F1-measure一直处于0.1以下，故图中未给出评估结果。

2.3 有向网络下非重叠社区CoDA算法的评估

数据集生成过程及数据集节点数的选取同2.2，节点平均度数、最大度数、混合参数、社区最小尺寸和最大尺寸等没有改变，只将重叠节点的个数和每个重叠节点属于的社区数调整为0。评估结果如图5和图6所示。

图5 链入成员评估结果图Fig.5 Evaluation result of incoming members

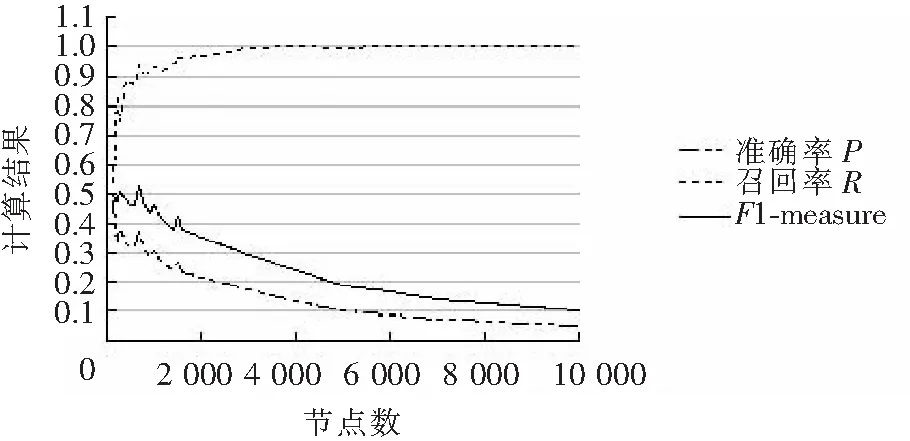
图6 链出成员评估结果图Fig.6 Evaluation result of outgoing members

通过对有向网络下非重叠社区CoDA算法的评估可以发现，在相同节点数据集下，链入成员资格和链出成员资格之间的准确率、召回率和F1-measure几乎相等。随着节点的不断增多，召回率不断升高，准确率和F1-measure在不断下降。这说明随着节点的增多，标准社区结构中不在同一社区的节点对经过CoDA算法处理后，被划分到同一社区的数量越来越多。标准社区结构中在同一社区的节点对经过CoDA算法处理后，被划分到2个不同社区的数量越来越少。到达10 000节点后，几乎所有属于同一ci社区的节点对都不会被划分到不同的社区内。数据集节点数量较小时，其综合性能较好；随着数据集节点数量的增多，其综合性能在逐渐变差。

分别对比有向网络下的重叠社区和非重叠社区的CoDA社区发现算法实验结果可知，相同节点的数据集下，重叠社区和非重叠社区之间的准确率、召回率和F1-measure相差很小，这说明CoDA社区发现算法在分别处理重叠社区和非重叠社区时，其稳定性非常好。

3 结 论

1) 将信息检索领域中的F-measure评价标准应用于社区发现算法的评估领域。既属于标准社区又属于某算法划分后，社区中的节点对数对应F-measure评价标准中检索出的相关文档数替换为算法划分后，社区中的节点对数对应该标准中检索出的文档数，真实社区中的节点对数对应该标准中文档库中所有相关文档数。通过实验可知，F-measure可以很好地刻画某社区发现算法对社交网络的社区划分结果与标准数据集中社区划分结果的差异，因此可以将该标准应用到有向网络下重叠社区和非重叠社区的挖掘算法评估领域。

2)在研究社交网络结构的过程中，一个准确的社区概念至关重要。传统模型认为“社区”是密集连接节点的集合。CoDA算法考虑了二分社区结构，它将一组在网络中没有直接链接，但链接在同一个坐标的节点组合在一起。该算法能识别有向网络下的重叠二分社区。当数据集节点数小于1 600时，CoDA算法社区划分效果较好且稳定，但是当节点数超过该值时，随着数据集节点数的增多，社区划分效果逐渐变差。因此，基于概率模型的CoDA社区发现算法适用于数据集规模较小时社交网络的划分，不适用于大规模社交网络的社区划分。

/References:

[1] NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69:026113.

[2] YANG J, LESKOVEC J. Overlapping community detection at scale: A nonnegative matrix factorization approach[C]// Proceedings of the Sixth ACM International Conference on Web Search and Data Mining. New York:ACM,2013:587-596.

[3] MAKINO K, UNO T. New algorithms for enumerating all maximal cliques[C]//9th Scandinavian Workshop on Algorithm Theory. Berlin:Springer, 2004:260-272.

[4] PALLA G, DERÉNYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435:814-818.

[5] EVANS T S, LAMBIOTTE R. Line graphs, link partitions, and overlapping communities[J]. Physical Review E, 2009, 80:016105.

[6] AHN Y Y, BAGROW J P, LEHMANN S. Communities and hierarchical organization of links in complex networks[J]. Nature, 2009, 466:761-764.

[7] WU Zhihao, LIN Youfang, WAN Huaiyu, et al. A fast and reasonable method for community detection with adjustable extent of overlapping[C]// 2010 International Conference on Intelligent Systems and Knowledge Engineering (ISKE).[S.l.]: IEEE Xplore, 2010:376-379.

[8] ANDREA L, FILIPPO R, RAMASCO J J, et al. Finding statistically significant communities in networks[J]. Inorganic Materials, 2002, 38(4):336-338.

[9] LANCICHINETTI A, FORTUNATO S, KERTÉSZ J. Detecting the overlapping and hierarchical community structure of complex networks[J]. New Journal of Physics, 2008, 11(3):19-44.

[10]SHEN Huawei, CHENG Xueqi, CAI Kai, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A:Statistical Mechanics & Its Applications, 2009, 388(8):1706-1712.

[11]LU Yinghua, MA Tinghuai, YIN Changhong, et al. Implementation of the fuzzy C-means clustering algorithm in meteorological data[J]. International Journal of Database Theory & Application, 2013, 6(6):1-18.

[12]NEPUSZ T, PETRCZI A, NÉGYESSY L, et al. Fuzzy communities and the concept of bridgeness in complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2008, 77:016107.

[13]PSORAKIS I, ROBERTS S, EBDEN M, et al. Overlapping community detection using Bayesian non-negative matrix factorization[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 83:066114.

[14]XIE J, SZYMANSKI B K, LIU X M. SLPA: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process[C]//2011 IEEE 11th International Conference on Data Mining Workshops(ICDMW). Vancouver: IEEE, 2011:344-349.

[15]RHOUMA D, ROMDHANE L B. An efficient algorithm for community mining with overlap in social networks[J]. Expert Systems with Applications, 2014, 41(9):4309-4321.

[16]FAGIOLO G. Clustering in complex directed networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 76:026107.

[17]NICOSIA V, MANGIONI G, CARCHIOLO V, et al. Extending the definition of modularity to directed graphs with overlapping communities[J]. Journal of Statistical Mechanics Theory & Experiment, 2009 (3):3166-3168.

[18]STEINHAEUSER K, CHAWLA N V. Identifying and evaluating community structure in complex networks[J]. Pattern Recognition Letters, 2010, 31(5):413-421.

[19]RAND W M. Objective criteria for the evaluation of clustering methods[J]. Journal of the American Statistical Association, 1971, 66:846-850.

[20]BEN-HUR A, ELISSEEFF A, GUYON I. A stability based method for discovering structure in clustered data[J]. Pacific Symposium on Biocomputing Pacific Symposium on Biocomputing, 2002(7):6-17.

[21]BRANDES U, GAERTLER M, WAGNER D. Experiments on Graph Clustering Algorithms[M]. Berlin: Springer, 2003:568-579.

[22]YANG J, MCAULEY J, LESKOVEC J. Detecting cohesive and 2-mode communities indirected and undirected networks[C]// Proceedings of the 7th ACM International Conference on Web Search and Data Mining. New York:WSDM, 2014:323-332.

[23]万里. 时间序列中的知识发现:基于频繁模式发现的分类和聚类方法研究[D]. 北京:北京邮电大学, 2009. WAN Li. Knowledge Discovery in Time Series：Researches on Classification and Clustering Based on Frequent Pattern Discovery[D]. Beijing: Beijing University of Posts and Telecommunications, 2009.

[24]LANCICHINETTI A, FORTUNATO S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80:016118.

Evaluation of the CoDA community detection algorithm based on directed network

GUO Song, ZHANG Dongwen, XU Yunfeng, YANG Yulin, ZHENG Yajie, LIU Chenguang

(School of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China)

CoDA (Communities through Directed Affiliations) algorithm is a kind of community detection algorithm which can successfully detect 2-mode communities based on probability model. TheF-measure criterion, for information retrieval, is adapted to the evaluation of CoDA algorithm in directed networks with overlapping communities or non-overlapping communities. The value ofF1-measure inF-measure criterion can reflect whether CoDA algorithm performs well or not. The data sets used in the experiment is generated by the LFR Benchmark tool. The minimum number of nodes in data set is 100 and the maximum is 20 000, and evaluated experiment is conducted when every 100 nodes is added. The results show that CoDA algorithm performs well when the number of nodes is bellow 1 600. CoDA algorithm's performance becomes worse with the increase of the number of nodes, which proves the CoDA algorithm based on probability model is applicable to the community detection of small-scale networks.

theory of algorithm; community detection; CoDA algorithm; directed networks; evaluate;F-measure

1008-1542(2017)02-0169-07

10.7535/hbkd.2017yx02011

2016-09-23；

2017-03-06；责任编辑：陈书欣

国家自然科学基金(71271076)

郭 松(1991—)，男，河北石家庄人，硕士研究生，主要从事聚类、社区发现方面的研究。

张冬雯教授。E-mail：zdwwtx@163.com

TP391.1

A

郭 松，张冬雯，许云峰，等.有向网络下的CoDA社区发现算法评估[J].河北科技大学学报,2017,38(2):169-175.

GUO Song,ZHANG Dongwen,XU Yunfeng，et al.Evaluation of the CoDA community detection algorithm based on directed network[J].Journal of Hebei University of Science and Technology,2017,38(2):169-175.