基于AHP-模糊综合评价法的山区丘陵公路灾害易损性研究——以河南省修武县为例

刘洋洋, 李永强, 李有鹏, 杨清科

(河南理工大学 测绘与国土信息工程学院，河南 焦作 454003)

基于AHP-模糊综合评价法的山区丘陵公路灾害易损性研究
——以河南省修武县为例

刘洋洋, 李永强, 李有鹏, 杨清科

(河南理工大学 测绘与国土信息工程学院，河南 焦作 454003)

以河南省修武县某山区丘陵公路为例，结合当地实际情况，先从社会因素、道路因素、防治因素三大方面进行考量考察，选取经济密度、人口密度、公路等级等8个因子为参评因子，建立公路灾害易损性评估层次结构模型，再采用AHP-模糊综合评价法实现公路灾害易损性的定量和定性综合评估，并提出相应的防治建议。研究结果表明，研究区公路灾害易损性极大，需进行重点防范；该研究评估方法与专家现场定性分析法取得的结果基本一致,体现出了较高的准确性和适用性，可为后续的山区丘陵公路防灾减灾工作提供一定的参考作用。

河南修武；山区丘陵；公路灾害；易损性评估；AHP-模糊综合评价法；防灾减灾

由于山区丘陵公路独特的线状特征，导致在开挖过程中形成了大量的人工边坡，虽然在公路建设中已经对这些边坡采取了防护措施，但由于山区丘陵地质情况复杂多变，因此仍然存在着很多隐患，滑坡、崩塌及泥石流等灾害经常发生，给公路交通和人民安全造成了严重威胁，因此，针对山区丘陵公路进行灾害评估具有重大的实际意义[1]。目前，对于公路灾害的危险性及稳定性评估，国内外已经有很多相关研究且比较成熟，如Zayed T等利用层次分析法(AHP)对高速公路进行危险性评估[2]，赵欢等采用ArcGIS技术进行公路泥石流灾害危险性分区研究[3]，张立东等采用模糊评判法对天山某段公路进行危险性评估[4]，柳厚祥等利用模糊聚类理论对湖南某高速公路边坡进行稳定性评估[5]，林孝松等利用灰色模型和马尔科夫模型进行公路边坡安全性评价[6]。而对于公路边坡灾害的易损性评估，由于其涵盖的影响因素繁多复杂，且涉及多种交叉学科，因此目前研究案例较少，文献也相对较少，主要有田述军等基于公路功能进行公路灾害易损性评估[7]，李家春等利用GIS技术进行公路自然灾害易损性评价等[8]，其中大多研究只采用公路灾害可能造成的经济损失和人员伤亡作为灾害易损性评价的指标，参评因子过于单一，且评估方法也多以专家定性法为主，评估结果主观性较强。针对上述问题，本文以河南省修武县境内某典型山区丘陵公路为例，从社会因素、道路因素、防治因素三大方面综合了各种可能影响公路灾害易损性的主、客观因素，并利用AHP-模糊评价法实现了公路灾害易损性定量和定性综合评估。

1 公路灾害易损性评价因子

由于公路灾害易损性评估涉及的影响因子错综复杂，且各因子的影响程度也都不相同，因此将所有影响因子都进行指标化是不切实际的[9]，结合前人研究成果、专家判断及该地区实际情况，本文总结分析了3类8项公路灾害易损性评估的主要影响因子，并将其作为进行AHP-模糊综合评价的参评因子。公路灾害易损性评估层次结构模型如图1所示。

图1 公路灾害易损性评估层次结构模型

1.1 经济密度

经济密度表示单位面积内的GDP生产总值，密度值一般由公路附近各县或乡镇GDP除以其面积得到。当公路沿线区域经济密度越大时，公路灾害堵断公路可能造成的损失就越大，易损性也就越高。

1.2 人口密度

人口密度表示单位面积内居住人口数量，密度值由公路附近各县或乡镇人口数量除以其面积得到。当公路沿线区域人口密度越大时，公路灾害可能造成的人员伤亡越大，易损性也就越高。

1.3 公路等级

公路等级是评价公路易损性的核心指标。不同的公路等级,建设标准和公路设施完善程度也不相同。公路等级越高，投入的资金人力就越大，防护力度也就越强，相对的也就越安全。为便于评估，本文把研究区公路分为四个等级，其中一级包含高速公路。一般情况下，公路等级越高,公路灾害易损性就越低；反之，公路等级越低,公路灾害易损性就越高。

1.4 路基工程

路基是公路的承重主体,它在承受着土体及路面结构自身荷载的同时,还要承受车辆向下传递的荷载,所以其设计的合理程度，直接关系到公路灾害易损性的高低。路基工程设计越合理，路基越牢固，变形越小，公路灾害易损性也就越低，反之，路基工程设计越不合理，路基越不牢固，变形越大，公路灾害易损性也就越高。

1.5 路面工程

路面作为车辆荷载的主要承载体,其易损性高低与公路本身的使用寿命及灾害抵御能力息息相关。路面工程设计越合理，公路抗灾能力越强，公路灾害易损性就越低；反之，路面工程设计越不合理，公路抗灾能力越弱，公路灾害易损性就越高。尤其是在公路灾害比较严重的地区,采用科学合理的路面设计结构,可提高路基路面的整体受力情况,从而在抵御滑坡、崩塌、泥石流等灾害冲击时起到较好的止损减损效果。

1.6 公路使用年限

公路使用年限是指公路在理想状态下可以安全运行的最大使用年数，同等规模的滑坡、崩塌灾害对于不同使用年限的公路造成的损害有着明显的区别。由于在实际运营中,公路很难满足其设计使用年限，因此该文选择公路已使用年限作为参评因子。公路已使用年限越少，公路老化程度越低，公路灾害易损性就越低；反之，公路已使用年限越多，公路老化程度越高，公路灾害易损性就越高。

1.7 防护完善程度

公路防护完善程度对公路灾害易损性高低有很大影响作用，是公路灾害易损性评估中的核心指标。公路防护完善程度越好，公路就越安全，公路灾害易损性就越低；反之，防护完善程度越差，公路就越危险，公路灾害易损性就越高。

1.8 养护维修力度

养护维修对公路的持续健康运营至关重要，是公路易损性评估中的关键指标。养护维修力度越大，公路更新改善越及时，公路灾害易损性就越低；反之，养护维修力度越小，公路更新改善越不及时，公路灾害易损性就越高。

2 关键方法

2.1 AHP法

AHP法(Analytical Hierarchy Process)即层次分析法，是美国著名学者satty于1973年提出的一种多准则多目标的权重决策方法，该方法能有效将定性与定量分析相结合，适用于准则较多、结构庞大且不易量化的复杂问题。层次分析法的核心思想是把问题层次化，即将一个复杂问题简化为决策方案(最底层)与总目标(最高层)之间相对重要性及权值确定的排序问题[10-11]。其具体实现步骤如下：①首先确定问题的性质和要实现的总目标，并把这个复杂问题分解成多级组成因素，从而建立一个有序的层次递进结构模型；②对每一层中全部因素的相对重要性进行判断，一般选用1～9标度法来进行两两比较(表1)；③确定每一层中各个因素的相对重要性次序，然后构建相应的判断矩阵，计算特征向量及其对应的最大特征根，特征向量归一化后的数值即为各因素的权重值；④最后对矩阵的一致性进行判断，当矩阵随机一致性比率CR<0.1时，即认定判断矩阵满足一致性检验，说明权重分配是合理准确的。

表1 1～9标度值及两种因素相对重要性比较含义

2.2 模糊评价法

模糊评价法即指对受多种模糊因素影响的现象或事物进行综合评价，该方法借助模糊数学来分析下级因素对上层事件的影响状态，通过层层推进，最终计算出各个因素对总目标的影响情况[12]。自然语言最大的特色就是它有一定的模糊性，一般来说，模糊事件或现象不能用0或1的二值逻辑来直接描述，而是要采用区间[0,1]的连续值来进行客观描述。相比多指标评判法等方法，模糊评价法能有效将定性事件定量化，其具体实现步骤如下：①建立参评因素集U；②建立评价集B；③确定隶属函数，计算各因素隶属度；④构造模糊关系矩阵，并计算出最终的评价结果。

2.3AHP-模糊综合评价法

AHP-模糊综合评价法，即基于层次分析(AHP)的模糊综合评价法，是一种将AHP法和模糊评价法结合使用的方法[13-14]。由于模糊评价法的指标权重大多是专家学者们通过主观判断得出，因此评估结果准确性不高，而层次分析法是将人的主观判断用数值形式进行描述的评估方法，它能有效减少个人主观臆断所造成的模糊性和不确定性，将层次分析法和模糊评价法进行有机结合，各取长处，相辅相成，可确保最终的评价结果准确科学，具体实现流程如图2所示。在进行山区丘陵公路灾害易损性评估时，由于公路灾害与山区丘陵地形之间的变量关系错综复杂，对于公路灾害易损性的影响因素，既有确定的一面，也有模糊的一面，“非此即彼”地准确判定不能真实描述参评因素对公路易损性的影响，“亦此亦彼”地模糊判定才能客观体现参评因素对公路灾害易损性的真实作用，因此，AHP-模糊综合评价法是进行公路灾害易损性评估的优良选择。

图2 AHP-模糊综合评价法

3 实例分析

3.1 研究区概况

修武县地处河南省西北部，太行山南麓，隶属于焦作市，位于35°07′39″～35°28′32″N，113°08′17″～113°32′03″E之间，人口约28.2万，面积约676.4 km2，国民生产总值(2014年GDP)约111.3亿元。修武县北部为山区和丘陵，南部为冲积平原，县区地势北高南低，属暖温带大陆性季风气候，春夏秋冬四季分明，年平均降雨量560.4 mm，地震基本烈度为Ⅶ度区。由于修武县境内有典型的山区丘陵公路地形，符合本文研究目的，因此选择该地区作为实验区域。经实地考察及焦作公路局提供资料可知，研究区公路建成于2004年，已运营12年，全长约21.6 km，属于三级公路，该区域地下水资源丰富，公路边坡植被覆盖率13.5%左右，公路灾害以滑坡、崩塌为主，坡体结构为层状，主要出露岩石类型有灰岩、白云岩、石英砂岩等，多为厚层或巨厚层状，岩体完整，致密坚硬，抗压强度高，抗风化能力强，土体类型主要为砾质土、砂性土、粘性土，局部还有淤泥质土。根据专家分析判断及前人研究成果，定义参评因子指标值越小，公路灾害易损性越低，经综合考量分析，分别将文中定性因子的分级标准量化值赋值为：0.1、0.3、0.6、0.9；对于经济密度、人口密度、公路使用年限等定量因子，采用实测数值进行描述；对于公路等级、路基工程、路面工程、防护完善程度、养护维修等定性因子，采用专家判断法来确定其量化值及隶属函数；经专家研究考证和数学分析，依次得出研究区公路等级、路基工程、路面工程、防护完善程度、养护维修五个定性因子量值为：0.70、0.45、0.05、0.75、0.80；公路灾害易损性评价标准和评价指标实测值分别如表2和表3所示。

表2 公路灾害易损性评价标准

表3 评价指标实测值

3.2 建立模糊集合

采用AHP-模糊综合评价法进行公路灾害易损性评估前，首先要建立参评因子和评价标准的模糊集合，具体内容如下所示。

(1)建立参评因素集U

U={U1,U2,U3}。

(1)

式中：U1表示经济因素集；U2表示道路因素集；U3表示防治因素集。

(2)建立参评因素的二级因子集C

C(u1)={C1,C2}；

(2)

C(u2)={C3,C4,C5,C6}；

(3)

C(u3)={C7,C8}。

(4)

式中：C1表示经济密度；C2表示人口密度；C3表示公路等级；C4表示路基工程；C5表示路面工程；C6表示公路使用年限；C7表示防护完善程度；C8表示养护维修力度。

(3)建立模糊综合评判集B

B={B1,B2,B3,B4}={Ⅰ,Ⅱ,Ⅲ,Ⅳ}。

(5)

式中：B1表示易损性低，B2表示易损性中等，B3表示易损性高，B4表示易损性极高。

3.3 确定参评因子权重

3.3.1 建立层次结构模型

权重是在综合评估时权衡各个因子相对重要性的数值，它主要用来反映不同因子间重要性程度的大小差异。公路灾害易损性评估拥有繁多复杂的影响因子，不同因子对公路影响程度也不相同，因此在进行易损性评估时要对不同的因子赋予不同的权重[16-17]。本文主要采用层次分析法来确定各个因子的权重，首先以公路灾害易损性评估为总目标，以社会因素、道路因素、防治因素为准则层，以二级参评因子为方案层，建立一个整体层次结构模型,如图1所示。

3.3.2 构造判断矩阵

根据研究区实际情况，结合专家意见，本文选用1～9标度法依次对公路灾害易损性评估的各项参评指标相对重要性进行两两比较，赋予A～U、C1～C8相应的权重值，并在此基础上，构造4个判断矩阵，分别为：A～U、U1～C、U2～C、U3～C。以U2～C为例，其判断矩阵如表4所示。

表4 U2～C判断矩阵

3.3.3 层次单排序及一致性检验

层次单排序是针对上层次中的某个元素，确定本层次与之有联系的各个元素相对重要性排序的权重值，其目的是解决判断矩阵的特征根和特征向量的计算问题。针对判断矩阵B，计算满足要求的特征根和特征向量：

BW=λmaxWi。

(6)

式中：λmax为B的最大特征根，W为对应于λmax的特征向量；Wi为对应于W的分量，即参评因子层次单排序的权重值。目前，求解判断矩阵的最大特征根及特征向量的主要方法为和积法或方根法。以U2～C判断矩阵中C3因子为例，本文采用方根法求解其最大特征根及特征向量，具体计算步骤如下所示。

(1)求解判断矩阵中C3行列(第一行)指标乘积M1,可得：

(7)

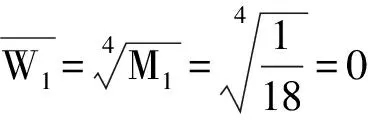
(8)

(3)进行归一化处理，计算权重W1，可得：

(9)

同理，根据上述步骤，可依次求出其他参评因子的层次单排序权重值。

计算出各因子层次单排序权重后，还需对结果进行一致性检验，以验证矩阵是否满足一致性。以U2～C判断矩阵为例，其一致性检验步骤如下：

(1)计算U2～C矩阵四个因子权重(W3,W4,W5,W6)的特征向量W，则有：

W=(W3,W4,W5,W6)T。

(10)

(2)计算判断矩阵的最大特征根λmax，可得：

(11)

式中：

(12)

(3)最后计算判断矩阵的一致性指标CI和随机一致性比例CR，可得：

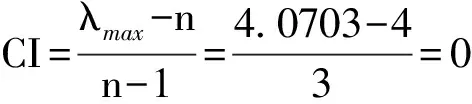
(13)

(14)

根据式(14)结果可知，该矩阵CR值小于0.1，满足一致性检验标准。采用上述步骤，可依次求出其他3个判断矩阵的层次单排序权重值及CR值。经计算，A～U等4个矩阵的一致性比例值CR均小于0.1，说明文中构造的判断矩阵是合理的、满足标准的。

3.3.4 层次总排序及一致性检验

计算出A～U等4个判断矩阵的层次单排序权重值后，根据从上到下的顺序，依次求出公路灾害易损性评估8个参评因子的层次总排序权重值，如表5所示，可得权重总矩阵：

A=[0.0423,0.1269,0.0465,0.1976,0.1262,0.0733,0.1291,0.2583]。

(15)

确定总排序权重后，还需检验其一致性比例CR，经计算，可得：

=0.0368<0.1。

(16)

式中：a1,a2, a3…a8分别表示各参评因子的总排序权重值，随机一致性指标RI值如表6所示。通过式(16)可知，层次总排序一致性比例值CR<0.1，说明其具有满意的一致性。

表5 参评因子层次总排序权重

表6 随机一致性指标值

3.4 确定隶属函数

确定各因子权重后，定义每个因子对应的不同公路灾害易损性等级为一个隶属函数，隶属函数一般包括梯形分布、半梯形分布、矩形分布、抛物线分布等，每种分布又分为偏小型、中间型及偏大型[17-18]。结合研究区公路实际情况及专家意见，本文最终定义隶属函数为降半梯分布函数。隶属函数如下所示：

(17)

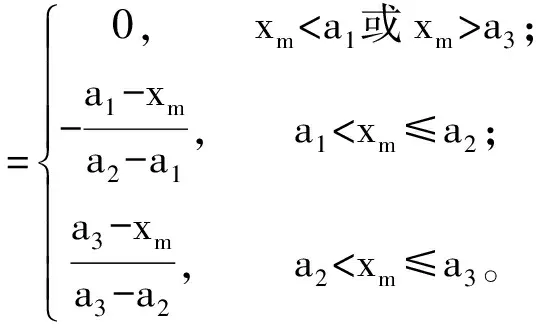
(18)

(19)

(20)

式中：xm表示第m个参评因子的实测值；bn(xm)表示第m个因子对第n级易损性评价级别的隶属度；a1,a2,a3,a4分别表示第m个因子(指标越小越安全)对应B1到B4四级公路灾害易损性评价等级的分界值。

3.5 构造模糊矩阵

将表2中各参评因子量化值依此代入公式(17)～(20)，每个因子可得到4个隶属函数方程，8个因子共32个矩阵。以经济密度C1为例，经计算，其模糊关系矩阵为：

RC1=[0,0,0.8875,1]。

(21)

同理，按照上述步骤，依次求出其他参评因子的模糊关系矩阵，最终可得到公路灾害易损性评估参评因子的模糊关系总矩阵R，则有：

(22)

3.6 综合评价

在上述步骤的基础上，将参评因子权向量A和其模糊关系总矩阵R进行结合，就可得出最终的公路灾害易损性模糊综合评判结果B，则有：

B=A·R=[0.1262,0.1574,0.3326,0.8740]。

(23)

根据最大隶属度原则[20]，其中最大隶属度Bi所对应的位置即为评判目标的最终危险级别。因此，由式(23)可知，该处公路灾害易损性级别的最大隶属度为B4=0.874 0=Ⅳ，即该地区公路灾害易损性极高，需进行重点防范。在此之前，专家对研究区公路灾害易损性进行的现场定性分析，得到以下结论：①该处公路为县道，公路等级较低，已使用年限较长；②路基路面结构设计一般，路面有较多毁坏待修区域，防护设施不够齐全，养护维修不够及时；③附近有两处风景区，经济密度大，人口密度也大，尤其是在“五一”和“十一”黄金周期间，人口密度会达到一个峰值；④经综合分析，专家一致认定该处公路灾害易损性较严重，需加强防灾减灾力度，防患于未然。最后，将两种结论进行对比分析可知，AHP-模糊综合评价法与专家现场定性分析法取得的评估结果大体吻合，说明该方法对山区丘陵公路进行灾害易损性评估是可行的。

3.7 防治建议

根据AHP-模糊综合评价法取得的评估结果，并结合研究区实际情况及专家意见，本文提出了一些具有针对性的防灾减灾建议。

(1)由于研究区公路位于净影寺和云台山两大风景区附近，在春秋两季的旅游旺季时期，尤其是“五一”和“十一”黄金周期间，人流量大，人口密度也大，公路灾害易损性较高，此时应对该区域公路边坡进行重点检查，排除危岩体，消除山体落石、崩塌隐患。

(2)最近几年暴雨天气较多，极易引起山体滑坡，在条件允许的情况下，公路部门可在该区域增设若干灾害监控站，利用三维激光扫描仪及配套的点云数据处理软件对人流量较大的公路地区进行实时监测扫描，观察边坡位移量和位移速度，并设定安全阈值，当边坡位移量和位移速度超过安全阈值时，系统将自动报警，公路部门可随即发布安全通知并疏散人群，以及进行相应的排险处理。

(3)公路部门应和灾害管理部门进行协同合作，根据该区域实际情况，拟定具有针对性的灾害预防治理方案，投入更多人力物力到该区域公路的养护维修中，完善路基路面的防护设施，提高公路抗灾防灾能力，降低公路灾害易损性。

4 结论

(1)针对目前山区丘陵公路灾害易损性评估案例较少且多为定性评估的问题，本文以河南省修武县某典型山区丘陵公路为例，采用AHP-模糊综合评价法实现了公路灾害易损性定定量和定性综合评估，并提出了相应的防治建议。研究结果表明，文中方法取得了良好的评估效果，与专家现场定性分析结果基本一致，体现出了较高的准确性、客观性以及适用性。

(2)针对目前山区丘陵公路灾害易损性评估参评因子较为单一的问题，本文从社会因素、道路因素、防治因素三大方面进行了多角度多层次的考量考察，确定了3类8项山区丘陵公路灾害易损性评估的主要参评因子，分别为：经济密度、人口密度、公路等级、路基工程、路面工程、公路使用年限、防护完善程度、养护维修力度。

(3)本文为山区丘陵公路灾害风险评估模型的前瞻性研究，后续在具备多期公路边坡三维激光点云数据时，会将测绘学科的先进技术理念与其他交叉学科进行有机结合，并应用到山区丘陵公路灾害风险评估研究中，目的是建立一个新的、完整的、具有较强适用性和科学性的山区丘陵公路灾害风险评估模型，为公路防灾减灾研究提供一种新思路。

[1] 张从明. 公路边坡治理措施及安全评价方法[M]. 北京:人民交通出版社, 2009.

[2]ZayedT,AmerM,PanJ.AssessingriskanduncertaintyinherentinChinesehighwayprojectsusingAHP[J].InternationalJournalofProjectManagement, 2008, 26(4):408-419.

[3] 赵欢, 田伟平, 李家春, 等. 公路泥石流灾害危险性分区研究[J]. 灾害学, 2016, 31(2):24-29.

[4] 赵立冬, 傅荣华, 张博. 天山公路沿线地质灾害危险性模糊综合评判——以K576+800～K690+000段为 例[J]. 防灾减灾工程学报,2007,27(1): 96-100.

[5] 柳厚祥, 胡勇军, 曹志伟,等. 基于模糊聚类理论的公路边坡稳定性分区研究[J]. 公路交通科技, 2015, 32(5):49-55.

[6] 林孝松. 山区公路边坡安全评价与灾害预警研究[D]. 重庆：重庆大学, 2010.

[7] 田述军, 孔纪名, 陈泽富. 基于公路功能的边坡灾害易损性评价[J]. 地球科学与环境学报, 2013, 35(3):119-126.

[8] 李家春, 尹超, 田伟平, 等. 中国公路自然灾害易损性评价[J].北京工业大学学报,2015,41(7):1067-1072.

[9] 任占伟. 公路滑坡风险性评价体系研究[D]. 西安：长安大学, 2010.

[10]许树柏. 层次分析法原理[M]. 天津：天津大学出版社,1988.

[11]王思长, 折学森, 周志军,等. 基于层次分析法的工程模糊集理论在公路边坡稳定性评价中的应用[J]. 安全与环境学报, 2010, 10(5):189-192.

[12]李柏年. 模糊数学及其应用[M]. 合肥：合肥工业大学出版社, 2007.

[13]韩利, 梅强, 陆玉梅,等. AHP-模糊综合评价方法的分析与研究[J]. 中国安全科学学报, 2004, 14(7):86-89.

[14]赵龙. 基于改进的AHP-模糊综合评价法的高速公路路线安全性评价研究[D]. 广州：华南理工大学, 2011.

[15]兰继斌, 徐扬, 霍良安,等. 模糊层次分析法权重研究[J]. 系统工程理论与实践, 2006, 26(9):107-112.

[16]王玮, 张玉芝. 模糊AHP的权重向量求解方法研究[J]. 控制与决策, 2006, 21(2):184-188.

[17]田伟平, 马保成, 舒淼. 山区沿河公路路基水毁灾害易损性评价[J]. 自然灾害学报, 2011,20(5):125-130.

[18]夏卜敬. 基于模糊综合评价和神经网络对边坡稳定性的分析研究[D]. 武汉：武汉科技大学, 2008.

[19]陈耀辉, 孙春燕.模糊综合评判法中的最大隶属原则有效度[J].重庆师范学院学报:(自然科学版), 2001, 18(1): 45-47.

Research of Highway Disaster Vulnerability Based on AHP-Fuzzy Comprehensive Evaluation Method: A Case Study of Xiuwu County in Henan Province

LIU Yangyang, LI Yongqiang, LI Youpeng and YANG Qingke

(CollegeofSurveyingandMapping,HenanPolytechnicUniversity,Jiaozuo454003,China)

TakinghillyandmountainousareahighwayofXiuwuCountyinHenanProvinceasanexample,combinedwithlocalactualsituation,weinvestigatefromthreeaspectsassocialfactors,roadfactorsandcontrolfactors,andselectingeconomicdensity,populationdensity,roadgradeselectionetc.eightfactorastheevaluatingfactors,establishingthehighwaydisastervulnerabilityhierarchyassessmentmodel,achievethehighwaydisastervulnerabilityquantitativeandqualitativeevaluationbyusingAHP-fuzzycomprehensiveevaluationmethod,finally,accordingtotheevaluationresults,weputforwardthecorrespondingsuggestionsonpreventionandcontrol.Researchresultsshowthattheregionalhighwaydisastervulnerabilityisgreat,needtofocusonprevention;theresultsobtainedinthispaperarebasicallyconsistentwiththeresultsobtainedbytheexpertsinthefieldofqualitativeanalysis,reflectingthehigheraccuracyandpracticality,andthenhasalsoprovidesomereferencevaluetothesubsequentriskresearchofhighwayinmountainousandhilly.

XiuwuCountyinHenanProvince;mountainousandhilly;highwaydisaster;vulnerabilityassessment;AHP-fuzzycomprehensiveevaluationmethod;disasterpreventionandreduction

2016-07-20

2016-08-29

国家“十二五”科技支撑项目 (2012BAH34B00)；国家自然科学基金项目 (41501491)；国家测绘局测绘地理信息公益性行业科研专项项目 (201412020)

刘洋洋(1991-)，男，河南许昌人，博士研究生，主要从事地理空间信息应用及灾害风险评估研究. E-mail：975492655@qq.com

李永强(1976-)，男，河南许昌人，博士，副教授，主要从事三维激光扫描及移动激光测量方面研究. E-mail：liyongqiang@hpu.edu.cn

10.3969/j.issn.1000-811X.2017.02.006.]

X43

A

1000-811X(2017)02-0032-07

10.3969/j.issn.1000-811X.2017.02.006

刘洋洋, 李永强, 李有鹏，等. 基于AHP-模糊综合评价法的山区丘陵公路灾害易损性研究—以河南省修武县为例[J]. 灾害学，2017，32(2)：32-38. [LIU Yangyang，LI Yongqiang，LI Youpeng, et al. Research of Highway Disaster Vulnerability Based on AHP-Fuzzy Comprehensive Evaluation Method：A Case Study of Xiuwu County in Henan Province [J]. Journal of Catastrophology，2017，32(2)：32-38.