三棱钻杆粉体负载扭矩计算模型研究*

薛　斐

(中国矿业大学(北京) 资源与安全工程学院，北京 100083)

0　引言

近年来，随着煤矿开采深度的增加，在深部煤层中，具有突出危险性的松软煤层愈加频繁，直接影响了煤矿的安全生产。松软煤体是区域地质活动的产物，自身力学强度较低，瓦斯含量、压力普遍偏高。对于松软煤层高瓦斯问题而言，只有通过有效抽放才能使煤体充分卸压，保障掘进、回采工艺。然而，松软煤层自身力学强度极低，在打钻过程中经常出现塌孔、堵孔问题，严重制约了瓦斯抽采钻孔的施工。

目前，在松软煤体中打钻一般选择风力排渣方式，主要钻杆之一即是三棱钻杆[1]。三棱钻杆抗弯折能力较强，在自转的同时，可以充分搅动钻孔内煤粉，使煤粉呈悬浮状态，大大增加了风力排渣的效率，在软煤打钻中具有较突出的应用前景。

国内外学者对于三棱钻杆的研究工作主要集中在以下两个方面：一是针对三棱钻杆应用效果的现场试验[1-6]；二是针对三棱钻杆强度问题的断裂分析与研究工作[7-12]。然而，对于三棱钻杆排粉过程中的扭矩计算问题，国内外学者并未作详细研究，相关文献较少[13-15]。

随着煤矿井下对瓦斯抽放问题越来越重视，松软煤层的钻孔问题亟待解决。在这个问题上，只有充分分析和研究三棱钻杆的排粉过程，才能更好地利用三棱钻杆完成松软煤层地成孔，最终保障煤矿井下人员的安全生产。

因此，本文针对三棱钻杆的转动排粉问题，提出假设并建立转动物理模型，得到了模型参数的解析解，对于三棱钻杆排粉动力学研究工作具有参考价值。

1　基本假设

1.1　三棱钻杆排粉过程分析

三棱钻杆具有3个圆弧形棱边结构，该结构可以不断地对煤粉形成搅动，为了进一步充分利用该优势，钻杆外棱直径一般会接近钻孔孔壁直径。这对于三棱钻杆搅动煤粉具有重要作用。

在一般工况条件下，三棱钻杆高速转动，3条圆弧棱边结构充分搅动钻孔内煤粉颗粒群。环向方向上，煤粉颗粒群在棱边结构搅动下，环向速度不断提升，最终在棱边结构与钻孔孔壁的合力作用下，达到与三棱钻杆相同的角速度共同旋转；轴向方向上，压风风流从孔底流向孔口，由于三棱钻杆的高速搅动作用，煤粉颗粒无法沉积，只能在断面呈悬浮状态，风流充分携带煤粉排出孔外，达到高效排粉的目的。

在排粉过程中，钻杆仅存在自转现象，因此对煤粉仅存在环向作用力，不存在轴向推动力；同理，风流与煤粉的作用仅存在于轴向方向上，并无环向作用。可以认为，煤粉颗粒群的轴向运动与环向运动是彼此独立的。

三棱钻杆在高速转动过程中，对于煤粉的搅动作用非常大，远远大于煤粉颗粒自身的重力，因此，煤粉颗粒的自重在这一过程中可以忽略不计。

1.2　基本假设的提出

基于以上分析结果，提炼出以下基本假设：

1)三棱钻杆自转仅与煤粉环向运动有关，与煤粉轴向运动无关。

2)三棱钻杆圆弧棱边与孔壁接近，呈准接触状态。

3)煤粉在三棱钻杆的高速搅动下，呈准充填状态，均匀分布于排粉空间。

4)环向方向上，三棱钻杆与煤粉共速、匀速运动。

5)环向方向上，煤粉颗粒群整体运动，不考虑层间相对滑动。

6)煤粉质量与钻杆搅动力相比十分小，可忽略不计。

2　物理模型的建立

三棱钻杆的棱边结构搅动煤粉是环向运动过程，而煤粉轴向与环向运动过程是彼此独立的。因此在构建物理模型时，可以忽略钻孔内部煤粉轴向运动过程，仅考虑与轴向垂直的断面内部的运动过程，如图1(a)所示。

在钻孔断面内，圆弧棱边结构十分接近孔壁，可以保证对于绝大多数煤粉的搅动作用。同时，在环向运动稳定后，也即煤粉颗粒群在合力作用下与棱边结构共速转动过程中，棱边结构可以直接推动煤粉颗粒群整体运动，而不会产生煤粉颗粒群层间相对运动。

如图1(a)所示，三棱钻杆断面结构中存在一个自转区，该区域在三棱钻杆自转过程中同步自转。但是，该自转区与煤粉颗粒群呈点接触(断面方向)，且无限小，因此在模型构建过程中，该区域不参与煤粉颗粒群运动过程。

在忽略中心自转区后，三棱钻杆的实际作用结构仅存三个类三角结构，而这三个类三角结构完成了对煤粉颗粒群的环向作用。在这一过程中，自转区等同于静止不动，而类三角结构在自转区上滑动，滑动的过程中对煤粉颗粒群产生环向作用，而这一作用主要是由类三角形运动方向的迎面提供。因此，在对煤粉作用的过程中，不考虑背面相互作用力。对于圆弧面而言，曲率与钻孔曲率相同，在煤粉运动过程中，仅存在环向摩擦力；又因为该结构远远小于三角形的长边，因此在模型构建中可以忽略。

图1(b)给出了稳定状态下钻孔断面的力学模型，钻孔半径为R，棱边结构半径近似等于R，此时煤粉颗粒群在合力作用下均匀分布于钻杆与孔壁的间隙内，张角为2θ。分析可知，煤粉颗粒群受到类三角结构迎面施加的垂直作用力FN、由于相对滑动的趋势而产生的摩擦力f、孔壁对煤粉颗粒群施加的反作用力F反以及相对滑动产生的反向摩擦力f反。在与径向垂直的方向上，类三角形与孔壁对煤粉颗粒群的摩擦力互相平衡；在径向方向上，煤粉颗粒群在孔壁与类三角形的合力提供的向心力的作用下，绕钻孔中心作匀速圆周运动。

3　物理模型的求解

3.1　求解过程

1)主方程组表达式

由于实际打钻过程存在于三维空间，各项参数也是在三维空间求取的，计算模型的求解过程必须符合三维空间量纲。因此，在钻孔轴向方向上取单位长度进行分析计算，基于上述物理模型，轴向单位长度上煤粉颗粒群运动过程满足下列主方程组，

(1)

式中：F反为孔壁对煤粉颗粒群的反作用力，N；FN为钻杆对煤粉颗粒群的作用力，N；f为钻杆对煤粉颗粒群的摩擦力，N；f反为孔壁对煤粉颗粒群的摩擦力，N；m为煤粉颗粒群质量，kg；r为煤粉颗粒群质心相对于钻孔中心的距离，m；w为煤粉公转角速度，也即三棱钻杆自转角速度，rad/s。

2)FN，f的表达式

设，类三角形结构迎面施加的正应力为σN，切应力(摩擦力)为τN，则

(2)

式中：σN为钻杆对煤粉颗粒群的正应力，N/m2；τN为钻杆对煤粉颗粒群的切应力，N/m2；R为钻孔半径，m；1代表单位长度，m；θ为煤粉覆盖张角的一半，rad；μ1为钻杆与煤粉的静摩擦系数。

3)F反，f反的表达式

由于煤粉颗粒群受到孔壁的反作用力相对于O-R线对称，因此仅考虑上半部的受力情况，如图2所示。设，孔壁对煤粉颗粒群的正应力为σ反、切应力(摩擦力)为τ反、孔壁任意位置与O-R线夹角为ψ。

在A-B方向上，钻杆长边与孔壁对煤粉颗粒群的摩擦力相等，也即τ反在A-B方向上的分力的积分与f相等，分量夹角为ψ；同理，在O-R方向上，σ反的分力的积分与FN的差值提供煤粉颗粒群的向心力，分量夹角同为ψ。

因此，F反，f反的表达式为:

(3)

式中：σ反为孔壁对煤粉颗粒群的正应力，N/m2；τ反为孔壁对煤粉颗粒群的切应力，N/m2；ψ为切应力τ反与A-B方向的夹角，rad；μ2为孔壁与煤粉的动摩擦系数。

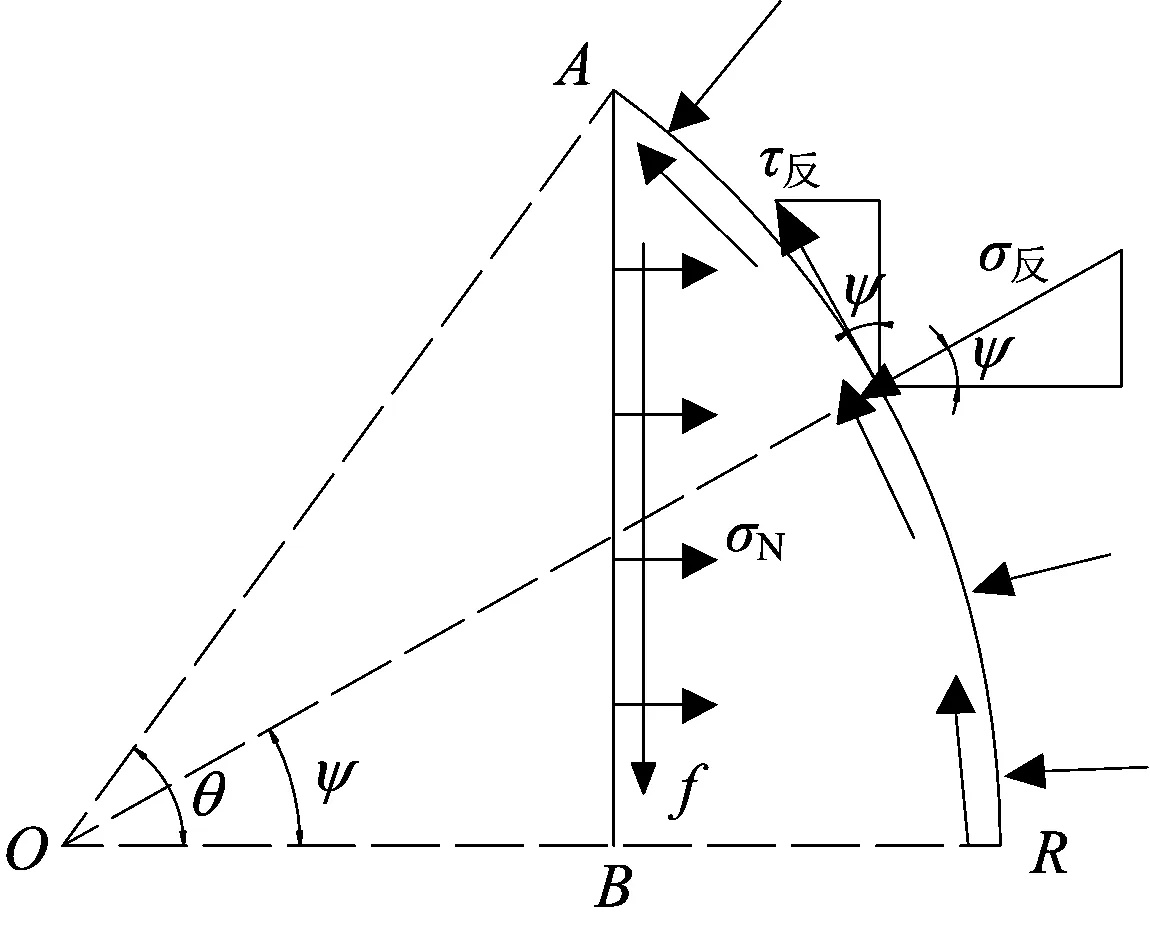
图2　煤粉颗粒群受力分析Fig.2　Stress analysis of coal particle swarm

4)m·r的表达式

由质心与静矩的关系式可知:

(4)

式中：So为煤粉颗粒群相对于O点的静矩，m3；A为煤粉颗粒群面积，m2；ρ为煤粉密度，kg/m3。

又因为煤粉颗粒群整体对于O点的静矩So等于各个微元长方体dA对于O点静矩dS的积分和，如图3所示，因此有:

(5)

式中：x为任意微元长方体质心到O点的距离，m；dx为微元长方体的宽度，m。

因此，m·r的表达式为:

(6)

图3　煤粉颗粒群静矩分析Fig.3　Static moment analysis of coal particle swarm

5)物理模型的求解

将式(2)、(3)、(6)带入式(1)，可得:

(7)

对上述方程组进行求解，得:

(8)

轴向单位长度上，由σN引起的扭矩Tσ、τN引起的扭矩Tτ分别为:

(9)

因此，三棱钻杆在工作过程中的总扭矩为:

(10)

式中：ρ为煤粉密度，kg/m3；L为钻孔长度，m；w为煤粉公转角速度，也即三棱钻杆自转角速度，rad/s；R为钻孔半径，m；θ为煤粉覆盖张角的一半，rad；μ1为钻杆与煤粉的静摩擦系数；μ2为孔壁与煤粉的动摩擦系数。

3.2　算例分析

根据假设可知，煤粉颗粒群在钻孔中处于高速运动状态，也只有在该状态下，颗粒群才可以完全充填于钻孔中，且均匀充填。同时，三棱钻杆主要用于软媒钻孔，孔内煤粉量较大。因此，假定钻杆转速为300 r/min，孔内煤粉颗粒群密度为1 000 kg/m3，钻孔半径为50 mm，煤粉覆盖张角为2π/3。根据文献[16-17]的研究结果与数据，采用煤粉与石墨类比的方法，取煤粉与不锈钢材料的静摩擦系数为0.6，煤粉之间的动摩擦系数为0.5。

当钻孔长度为20 m,50 m,80 m时，将上述数据带入式(10)并计算可知，由于煤粉颗粒群的负载造成的三棱钻杆的扭矩分别为T20=587.36 N·m，T50=1 468.41 N·m，T80=2 349.46 N·m。

以目前较为常用的全液压坑道钻机ZDY3200S作为分析对象，其最大扭矩为4 200 N·m。对比可知，当钻孔深度为20 m时，三棱钻杆上的煤粉负载只占到最大扭矩的14%左右，而当钻孔不断加深后，其扭矩占到最大扭矩35%和56%。

因此，随着钻孔深度的增加，排粉需求的增大，煤粉负载这一因素就越发凸显了其重要性，必须在打钻过程中予以考虑。

4　讨论

1)参数的意义及求取方法

公式中，各元素均为自变量，且对于扭矩存在不同程度的影响。然而在实际软煤打钻过程中，钻孔布局及钻孔参数信息一般是确定的(R固定)，这一参数可根据具体煤层的瓦斯抽采设计图确定；根据确定的钻孔参数可以确定不同的三棱钻杆尺寸，目前国内三棱钻杆的结构样式与煤粉覆盖张角是一致的(θ固定)，这一参数可根据具体钻杆尺寸确定；同时，对于某个特定煤层而言，其煤粉与钻杆、孔壁间的摩擦系数μ1、μ2也可以通过测定摩擦角而确定；转速w可以从钻机上得到。因此，这里重点讨论煤粉密度ρ的求取方法。

ρ为煤粉颗粒群的密度，直接受钻进速率和风力排渣速率的影响。该参数可以通过理论计算结合气力输送试验进行确定。假设钻孔半径为R，煤粉堆密度为ρ′，煤粉颗粒群原始密度为ρ0，钻机的钻进速度为v，环状间隙面积为A，环状间隙内压风风速为v风，煤体膨胀系数为β，环状间隙内压风风流在单位时间内的排渣能力为Q0。单位时间的产粉量Q产、排粉量Q0分别为:

(11)

式中：α为风力排粉系数，无量纲，表明煤粉运移速度与风速的比值，与风速v风和煤粉密度ρ正相关。对于不同的煤粉密度ρ以及不同风速v风，可以通过气力输送试验确定对应的单位时间排粉量，进而确定不同的α值。

在一定时间内，仅考虑额外钻进距离内，ρe的表达式为:

(12)

当ρe大于ρ0时，原始密度ρ0会被不断拉高，同时由于密度上升，排渣能力Q0不断提高，ρe不断降低，最终趋于平衡，煤粉颗粒群密度稳定在ρ1；相反，若ρe小于ρ0，ρ0会不断降低，排渣能力Q0不断减小，ρe不断上升，最终同样趋于平衡，稳定在ρ1。因此，存在一个稳定状态，煤粉密度稳定在ρ1。

假设在稳定状态时，煤粉密度为ρ1，则有等式：

(13)

2)最小扭矩问题

在煤矿井下软煤打钻过程中，最小扭矩的使用具有重要的意义：一方面利用最小扭矩进行钻进工作可以大大节约打钻过程中的用电量，同时，最小扭矩钻进也可以降低钻机、钻杆的损耗，这两点都可以大大降低煤矿打钻工作的成本；另一方面，当扭矩大于最小扭矩时，转速普遍偏高，煤粉对孔壁的摩擦力增大，磨损增加，孔壁稳定性降低，不利于打钻工作的顺利开展。

通过扭矩T的表达式可知，当煤层、钻孔信息确定后，扭矩仅受煤粉密度ρ以及转速w的影响。在基本假设中规定，煤粉颗粒群轴向运动与环向运动无关，也即煤粉密度ρ(受钻进速率与排粉速率影响)与转速w之间彼此独立。

由ρ的表达式可知，ρ受v与v风的直接影响。在排粉能力Q0不变的情况下，当钻进速度v降低时，产粉量Q产降低，煤粉密度ρ降低；在钻进速度v不变的情况下，当风速v风增加时，排粉量Q0增大，煤粉密度ρ降低。

然而，在实际打钻过程中，钻孔作业任务量较大，降低钻进速度v会降低生产效率，这与生产需要相抵触；同样的，由于煤矿井下压风系统风压一定，如需提高压风风速v风，必须安装风机提供额外风压，而这一过程不仅增加了投资，也消耗了人力与时间，因此不建议在钻机正常工作的状态下使用上述手段降低钻机扭矩。

基于上述分析，在实际打钻过程中，只有通过调节转速w才能够实现对于钻机扭矩的调节。但是，转速w并不是随意调节的，它具有一个调节范围。如图4所示，转速w存在一个临界转速w界，当w小于w界时，煤粉颗粒群发生沉积，无法形成准充填状态；只有当w大于w界后，煤粉颗粒群达到理想状态，扭矩可以按照本文提供方法进行计算。当然，w不能无限大，上限为钻机额定转速。因此，转速w在临界转速w界与额定转速间变化。当转速接近w界时，钻机扭矩接近最小扭矩，此时，在同等时间内完成等量打钻任务的情况下，该状态能耗最小。

图4　实际转速对煤粉颗粒群的状态影响对比Fig.4　Comparative analysis of influences of rotation speed on status of coal particle swarm

临界转速w界主要受煤粉密度、粒度参数的影响。在这里，提出一种利用相似模拟实验确定w界的方法：

首先，确定煤层、钻孔、打钻信息，并在煤层中试验打孔，测出煤粉的平均粒径。

其次，根据钻孔、钻杆信息制作与实际尺寸相等的相似模型，尽量选择轻质替代材料，腔体需透明，如图5所示。

第三，根据打钻信息确定煤粉密度ρ，将模拟煤粉(可用橡胶颗粒代替，对腔体无磨损污染，密度应与实际煤粉相似)按计算密度装入模型，不断增加转速，并利用肉眼进行观测，当颗粒群被全部搅动且底部无沉积时，认为达到临界转速w界，利用转速计测出转速，该值可直接用于井下实际生产中。

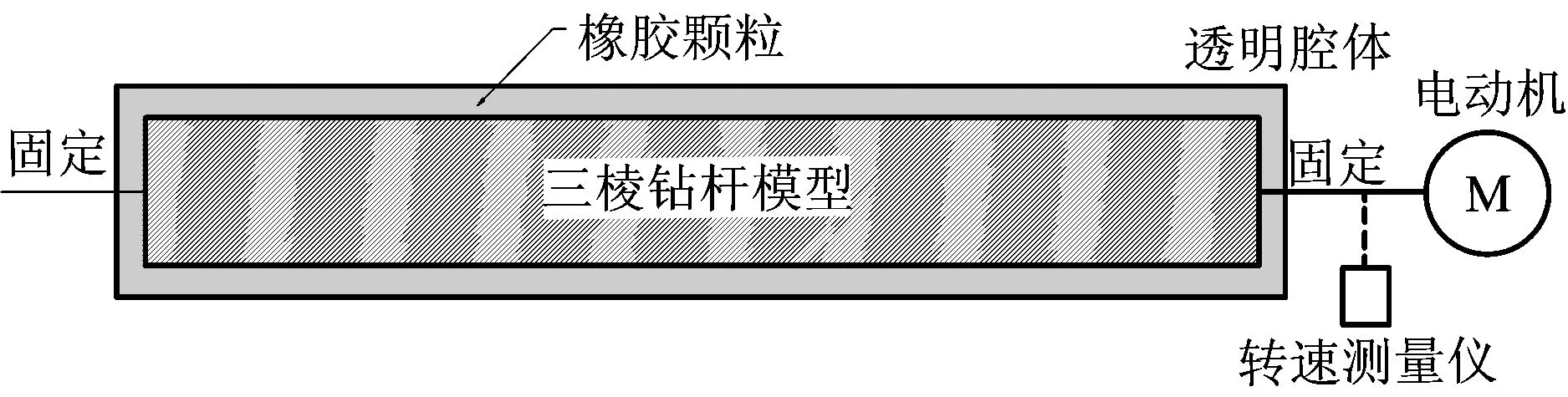
图5　相似模拟实验示意Fig.5　Diagrammatic sketch of analog simulation experiment on critical rotation speed

3)极限钻孔长度问题

基于扭矩T的表达式，在得到钻孔、钻机、钻杆、压风系统参数后，理论上可以求解钻孔的极限长度，并且可以根据需要适当调节相关参数以提高钻孔深度，见图6。

图6　极限钻孔长度多参数示意Fig.6　Multi-parameter relationship of maximum borehole length

一般情况下，钻孔半径R、煤粉覆盖张角2θ、摩擦系数μ1、μ2为已知参数；在三棱钻杆工作过程中，若要保持其正常工作、排粉舒畅，转速w需达到w界。

1)假设工作过程中由于压风风流、钻进速度控制良好，煤粉颗粒群密度ρ保持ρ1水平，则扭矩T与钻孔长度L呈正比，即T∝L。

2)随着钻孔深度的增加，扭矩T到达最大扭矩Tmax，理论上在保持正常排粉情况(w>w界以上)下钻机无法继续钻进。

3)在保持w界情况下，若要继续增加钻孔深度，需要不断降低煤粉颗粒群密度ρ，ρ与L服从反比例关系。

4)若要降低ρ，可以选择降低钻进速率v和提高压风风速v风。然而随着钻孔深度的增加，风阻增大，风速无法提高，因此只能选择逐渐降低钻进速度v以保证孔内煤粉被逐渐排出并保持在更低水平上。

5)在不断降低ρ的情况下，钻孔深度不断增加，但其存在一个极限长度，其极限长度为钻机可携带最大钻杆长度(无排粉负载)。

上述分析与实际情况较为吻合，在钻机扭矩足够情况下，可以保证在较高煤粉颗粒群密度水平(较高钻进速率)下钻进；当扭矩达到最大扭矩后，只能依靠降低钻机负载的方式提高钻进深度。

5　结论

1)通过对三棱钻杆排粉机理进行分析研究，提出了基本假设，并建立了三棱钻杆扭矩物理模型，得到了钻杆扭矩的解析解。随着钻孔深度的增加，煤粉负载在总扭矩中占比越来越大。

2)探讨了扭矩解析解中各参数的意义及其求取方法，并通过对煤粉群面密度ρ的分析，判断该参数可以是解析解，并求出了该解析解。

3)探讨了最小扭矩问题，转速w应在临界转速w界与额定转速间变化。当转速接近w界时，钻机扭矩接近最小扭矩，此时，在同等时间内完成等量打钻任务的情况下，该状态能耗最小。

4)提出了临界转速w界的实验测定方法，并得到了提高钻孔长度的理论方法。

[1]彭腊梅,李光,蒲天一. 松软突出煤层整体式三棱螺旋钻杆中试研究[J]. 煤炭科学技术, 2013, 41(8): 133-136.

PENG Lamei, LI Guang, PU Tianyi. Study on pilot test of integrated triangular helix drilling rod in soft and outburst seam[J]. Coal Science and Technology, 2013, 41(8): 133-136.

[2]Anders Willersrud, Mogens Blanke, Lars Imsland. Incident detection and isolation in drilling using analytical redundancy relations[J]. Control Engineering Practice, 2015, 41(8): 1-12.

[3]Yingfeng Meng, Hongtao Li, Gao Li, et al. Investigation on propagation characteristics of the pressure wave in gas flow through pipes and its application in gas drilling[J]. Journal of Natural Gas Science and Engineering, 2015, 22(1): 163-171.

[4]凌标灿,戴世鑫,曹承平,等. 三棱钻杆在中软煤层顺层瓦斯抽排钻孔的应用[J]. 煤炭科学技术, 2009, 37(10): 44-46.

LING Biaocan, DAI Shixin, CAO Chengping, et al. Application of triangular drilling rod to gas drainage borehole drilling in medium soft seam[J]. Coal Science and Technology, 2009, 37(10): 44-46.

[5]I. Popa, L.S. Stanciu. Stress and displacements analysis for drilling mast elements made of rectangular pipe: the overload test case[J]. Key Engineering Materials, 2014, 60(1): 120-123.

[6]王永龙,孙玉宁,翟新献,等. 棱状钻杆应用于松软突出煤层钻进强度匹配研究[J]. 中国安全生产科学技术,2014, 34(10): 48-54.

WANG Yonglong, SUN Yuning, ZHAI Xinxian, et al. Study on strength matching of prismatic drilling rod when drilling soft and outburst coal seam[J]. Journal of Safety Science and Technology, 2014, 34(10): 48-54.

[7]Jianshe Mao, Youhong Sun, Baochang Liu, et al. Research on interference connection of aluminium alloy drill pipe body-steel tool joint assembly[J]. International Journal of Earth Sciences and Engineering, 2014, 7(2): 533-539.

[8]赵金凤,余世杰,贾明宇,等. 三棱螺旋钻杆管体裂纹失效分析[J]. 金属热处理, 2013, 56(12): 118-121.

ZHAO Jinfeng, YU Shijie, JIA Mingyu, et al. Failure analysis on crack of triangular spiral drill pipe[J]. Heat Treatment of Metals, 2013, 56(12): 118-121.

[9]Yuanhua Lin, Xing Qi, Dajiang Zhu, et al. Failure analysis and appropriate design of drill pipe upset transition area[J]. Engineering Failure Analysis, 2013, 31(7): 255-267.

[10]Zhi Zhang, Jing Li, Dezhi Zeng, et al. Stress corrosion cracking of high-strength drill pipe in sour gas well[J]. Journal of Wuhan University of Technology(Materials Science Edition), 2014, 29(8): 813-816.

[11]肖丽辉,刘晓东,杨健. 三棱钻杆焊缝区断裂分析及解决措施[J]. 地质装备, 2013, 14(5): 22-24.

XIAO Lihui, LIU Xiaodong, YANG Jian . Failure analysis and solutions of welding area of triangular drill pipes[J]. Equipment for Geotechnical Engineering, 2013, 14(5): 22-24.

[12]W. Gerstle, T. McCarty-Glenn, S.F. Dwyer, et al. Leakage from drill pipe casing subject to shear deformation[J]. International Journal of Petroleum Engineering, 2014, 1(1): 49-61.

[13]王永龙,宋维宾,孙玉宁,等. 瓦斯抽采钻孔堵塞段卡钻扭矩力学模型分析[J]. 中国安全科学学报, 2014, 24(6): 92-98.

WANG Yonglong, SONG Weibin, SUN Yuning, et al. Analysis of pipe-sticking torque mechanical model for gas extraction borehole clogging segment[J]. China Safety Science Journal, 2014, 24(6): 92-98.

[14]Elisabeth Cheng, Maria Anna Polak. Theoretical model for calculating pulling loads for pipes in horizontal directional drilling[J]. Tunnelling and Underground Space Technology, 2007, 22(5-0): 633-643.

[15]徐连满,李祁,潘一山,等. 钻杆扭矩法预测冲击地压的研究[J]. 工程力学, 2014, 31(11): 251-256.

XU Lianman, LI Qi, PAN Yishan, et al. Study on forecasting rockburst of the drill pipe torque method[J]. Engineering Mechanics, 2014, 31(11): 251-256.

[16]张媛媛,沈湘林,汤雪美,等. 煤粉壁摩擦特性的实验与模拟[J].东南大学学报自然科学版, 2010, 40(1): 133-138.

ZHANG Yuanyuan, SHEN Xianglin, TANG Xuemei, et al. Wall friction characteristics of pulverized coal by experimental and numerical simulation[J]. Journal of Southeast University (Natural Science Edition), 2010, 40(1): 133-138.

[17]各种材料摩擦系数表[OL].(2013.5.4) http://wenku.baidu.com/link?url=gKWKENv9_QzwWLgeCVtoNKS_xbGdGS7 CUOlziCR8CZ8yTlB2goWWBbHByvk4e9EKi5_xcwyvJZpe3SAwen WEx9p3LavsHqn-MEbJkDcAVhe.

Diagram of friction factor of materials[OL]. (2013.5.4) http://wenku.baidu.com/link?url=gKWKENv9_QzwWLgeCVtoNKS_xbGdGS7CUOlziCR8CZ8yTlB2goWWBbHByvk4e9EKi5_xcwyvJZpe3SAwenWEx9p3LavsHqn-MEbJkDcAVhe.