灾后应急资源配送的LRP模型与算法研究*
2017-04-14易显强
戴 君,王 晶,易显强
(1.北京工业大学 应用数理学院,北京 100020; 2.北京工商大学 商学院,北京 100048)
0 引言
近年来自然灾害频发,2008年中国南方地区雪灾、汶川地震、2010年海地地震、2011年日本地震、2012年“7.21”北京特大暴雨灾害、2014年智利地震和云南鲁甸地震、2015年尼泊尔地震等,都给人们的生命和财产带来了巨大的损失。灾害发生后,快速高效的应急资源配送和供应,是灾后救援有效开展的前提,对于减少人员伤亡和灾害损失具有重要意义。灾后救援需要面临以下2个问题:应急资源配送中心定位问题,灾害发生后,为了快速高效地开展应急救援,首先应该确定应急资源配送中心的数量、位置以及配送中心与需求点的归属划分,协调应急资源的调度工作;应急资源配送路径优化问题,如何在灾后的复杂道路网络中选择可靠的通行路径,给出整体优化的应急资源配送方案,是灾后应急救援需要解决的关键问题。针对以上2个问题,应急救援应该在整体的基础上给出考虑应急配送中心定位的灾后应急资源配送可靠路径方案。因此,重点研究灾后应急资源配送的“定位—路径问题”(location-routing problem, 简称LRP)。
在LRP问题的研究方面,WASTON C等[1]将道路网络与配送车辆路径优化结合起来,研究多个需求点巡回的“选址—路线优化问题”。此后,不少学者都在此基础上对LRP模型进行研究。W. TAI等[2]在LRP模型里加入对车辆型号和最大处理能力的约束;S.ALUMUR等[3]以总成本最小为目标,建立危险废弃物的LRP模型,研究废弃物处理站的选址和运输路线;章海峰等[4]考虑网络节点的最大承受能力和车辆的容量限制,建立对应的LRP模型;徐琴等[5]以城市突发公共事件为背景,建立以应急救援时间满意度最大为目标的LRP模型。
近几年,在LRP问题的基础上,应急资源配送路径规划也成为研究的热点。BALCIK B等[6]针对应急配送中心到需求点这一阶段的应急物资调度与配置,建立基于车辆调度的应急物资配送系统;JOTSHI A等[7]考虑到地震后对应急医疗的需求,提出基于数据融合的应急医疗救援中的车辆调度和路径选择模型;ÖZDAMAR L等[8]将应急物资分配与车辆调度问题结合起来,以应急物资的未满足需求之和最小为目标进行建模,并用拉格朗日松弛算法求解;YI WEI等[9]将应急资源配置问题划分为车辆路径规划阶段和资源配送阶段,并改进蚁群算法对问题进行求解;RAHMAN S U等[10]在救援过程中,考虑运输方式、运输路径以及应急资源分配等问题,同时满足应急资源调度量最大和成本最小;刘春林等[11]研究带物资需求约束条件的多个出救点的应急物资配置问题;缪成等[12]研究应急救援中的应急物资和车辆整合问题,把配送问题分解成2个多目标问题,并采用拉格朗日方法取得最优解;应夏晖等[13]建立模糊环境下的应急资源配送机会约束规划模型,并设计智能算法解决该问题。
目前关于灾后应急资源配送问题的研究,大多针对交通路网的情况,忽略应急资源配送中心的定位对应急资源配送的影响,较少考虑定位与配送的集成优化。尽管有些文献研究应急资源配送的LRP问题,但模型较为简单,缺少定位对应急资源配送方案改变的刻画。在实际的应急救援中,配送中心的定位会影响到应急资源配送,进而影响应急救援效率。从整体出发,研究灾后应急资源配送LRP问题,将配送中心定位与应急资源配送可靠路径规划结合起来进行集成优化,对于提高灾后救援效率具有重要的理论意义和实际价值。
1 灾后应急资源配送LRP问题优化模型
1.1 问题描述
灾害发生后,在开展应急救援时,应根据灾区分布情况,建立应急资源配送中心,选择路径最短、可靠性最高的路径方案来协调应急资源的调度。快速建立应急资源配送中心对应急资源的调度具有重要意义,但是可能会导致应急资源配送的总路径长度增加。选择离受灾点较近的区域建立应急资源配送中心,能够就近为受灾点提供应急资源保障,但需要花费大量时间,容易耽误抢救的黄金时间。这就是LRP模型所要解决的问题,即在应急资源配送中心的定位和可靠路径方案中寻求平衡。如何在综合以上条件下,建立灾后应急资源配送LRP模型,给出全局最优条件下的应急资源配送中心定位方案和应急资源配送可靠路径方案,是需要解决的问题。
1.2 假设
1)网络中的节点分为3类,应急资源配送中心备选点、应急资源需求点和过渡节点,其中过渡节点可以认为是需求为0的应急资源需求点。
2)灾害发生后,需要在备选点里选择1个或多个点建立应急资源配送中心,然后从这些配送中心向需求点配送应急资源。
3)灾害发生后,道路网络受到影响,表现为每2个节点之间的道路都有通行可靠性,根据实际路况有所不同。
4)每个应急资源配送中心能够同时满足多个需求点的需求,但是每个需求点的需求只能由1个应急资源配送中心满足。
1.3 符号
n:网络中所有节点集合;
n(s):网络中应急资源配送中心备选点集合;
n(d):网络中应急资源需求点和过渡节点的集合;
ur:是否在r点建立应急资源配送中心;
Tn(s)r:在r点建立应急资源配送中心需要的时间,包括建立救灾中心、应急资源运抵的时间,假设与离灾害中心的距离有关;
zijt:t阶段是否选择通过i,j边,1表示通过,0表示不通过;
lij:不确定网络中边i,j的长度(路程);
pij:不确定网络中边i,j的通行可靠性;
TDk:配送车辆在道路正常的情况下的单位距离行驶时间;
si:网络中应急资源配送中心i的供应量;
dj:网络中需求点j的最低需求;
VQk:配送车辆k的容量限制;
eij:不确定网络邻接矩阵元素,eij=1表示i,j邻接,否则eij=0为不相邻;
yit:不确定网络中点i在阶段t的应急资源需求或者供应量,yit>0表示需求已满足,yit<0表示尚有需求未满足,yit=0表示是过渡节点;
xijt:t阶段通过i,j边的应急资源的流动量。
1.4 灾后应急资源配送LRP问题优化模型
以应急救援时间最短为目标,并对道路通行可靠性进行约束,即:
s.t.
yi1=si,i∈n(s)
(1)
yi1=-di,i∈n(d)
(2)
zijtxijt≤VQk
(3)
r∈n(s)
(4)
(5)
(6)
yiT≥0,i∈V
(7)
zijt≤eijt,i,j∈V,t∈T
(8)
(9)
(10)
xijt≥0
(11)
zijt,ur∈{0,1}
(12)
模型中,目标是总应急救援时间最短,包括2个部分:建立应急资源配送中心所耗费的时间;配送车辆在配送路径上所耗费的时间。约束(1),(2)初始化第1个时刻所有节点的应急资源数量;约束(3)表示车辆的最大处理能力约束;约束(4)表示在备选点集合里选择节点建立应急资源配送中心;约束(5)表示当前时刻的应急资源数量,等于上一阶段的所有量加上应急资源到达量,减去应急资源发出量;约束(6)限制从点i运出应急资源时,当且仅当i点已经获得满足;约束(7)保证到最后一个阶段时所有的需求点的需求都已获得满足;约束(8)表示当且仅当ij相邻时,应急资源方可从i点运输至j点,否则物资不能直接由i点运输至j点;约束(9)描述了车辆的不可分性,车辆只能选择网络中的1个点作为目的地;约束(10)要求每个需求点的需求只能由1个点来满足;约束(11)表示路径上的资源流动量不为负;约束(12)表示“0,1”约束。
2 模型求解的离散粒子群算法
由于该问题包含多阶段和变量,属于“NP-Hard”问题,难以通过精确算法对模型进行求解。同时,灾害条件下,需要在短时间内寻找1个相对最优的应急资源配送方案。启发式算法能满足该类问题的需求,其中粒子群算法能够避免复杂的遗传操作,精度高、收敛快,因此,选择粒子群算法进行求解。
2.1 粒子群算法简介
粒子群算法是近年来发展起来的1种新的进化算法,起源于对鸟群捕食的行为研究。通过模拟鸟群中个体间对信息的共享,相互协作,从而获得最优解。粒子群算法已被证明是1种有效的优化算法,由于容易实现、精度高等优点,一经提出就受到许多学者的关注,并且在解决实际问题中体现出优势。
粒子群算法中,每个解都是搜索空间中的1个粒子。所有的粒子都有1个适应值,适应值由优化函数决定。还有1个速度决定它们运动的距离和方向,粒子追随种群中的最优粒子在解空间中搜索。该算法初始化为1群随机粒子,通过迭代找到最优解。在每1次迭代中,粒子通过2个极值来更新自己,1个是粒子本身所找到的最优解,这个解叫做个体极值pBesti;另1个极值是整个种群目前找到的最优解,这个极值是全局极值gBesti。各粒子根据如下公式来更新自己的速度和位置:
Vid(t+ 1) =wVid(t) +c1r1[Pi d(t)-Xid(t)] +c2r2[Pgd(t)-Xid(t)]
(13)
Xid(t+1)=Xid(t)+Vid(t+1),
1≤i≤N,1≤d≤D
(14)
其中w表示惯性权重,学习因子c1和c2是非负常数,r1和r1是2个独立的介于[0,1]之间的随机数,体现了粒子的记忆行为。式(13)中的第1部分表示粒子的惯性速度,第2部分表示粒子的动作来源于自己的经验,第3部分表示粒子的动作来源于群体中其他粒子的经验。
2.2 应急资源配送优化模型的离散粒子群算法
粒子群算法在许多连续优化问题中得到了广泛的应用,但是在离散问题和非数值化问题方面则相对滞后。针对标准粒子群算法在解决离散问题上的缺点,采用文献[14]提出的1种改进的粒子群算法,引入次优吸引子,使粒子在搜索过程中可以充分利用群体信息,提高算法的搜索能力。在标准粒子群算法中,仅依靠调节w的大小来平衡种群的探索和开发能力是不够的,因为w值只能左右个体自身的速度。当个体粒子陷入局部收敛时,通过调节w值的大小只能使粒子跳出局部搜索区,而并没有考虑群体中的相互作用。因此,通过引入次优吸引子来提高种群的搜索能力,并引入收缩因子,使粒子可以根据适应值与平均值的大小动态调节参数。
改进后的粒子群算法的公式为:
Vid(t+ 1) =k(wVid(t) +c1r1[Pi d-Xid(t)] +
(15)
Xid(t)) +c3r3(pc-Xid(t))])
Xid(t+1)=Xid(t)+Vid(t+1),
1≤i≤N,1≤d≤D
(16)
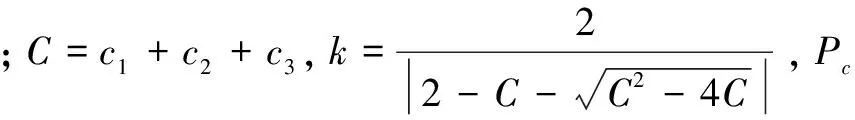
Pc=arg min
{f(Pid|i=1,…,n,且Pij≠Pgd}
(17)
2.3 编码方式
如何找到1个合适的表达方法,使粒子与解对应,是实现算法的关键问题之一。构造M个应急资源配送中心,N个需求点,K辆配送车辆的粒子编码,其中位置向量X可表示为(x1,x2,…,xM+N+K),每个元素x1取值为1到M+N+K之间互不相同的整数。改进的多吸引子的离散粒子群优化算法,通过对粒子的合理编码能够快速求解模型,同时避免局部最优解。
2.4 算法步骤
1)设定种群中的粒子数和最大迭代次数,各粒子的初始位置和初始速度随机;
2)计算每个粒子的适应值;
3)对每个粒子,更新Pid和Pgd;
4)对每个粒子,根据式(17)更新Pc;
5)根据式(15)和式(16)更新粒子的速度和位置;
6)如果达到预期,或迭代的次数等于最大迭代次数,转7),否则转2);
7)输出最优结果。
3 仿真与分析
以某区域内地震灾害条件下的应急资源配送与调度为例,假定有6个应急资源配送中心备选点,16个应急资源需求点,若干个过渡节点。假定只考虑1种物资,由于人员、资源等所限,应急资源配送中心的数量不超过备选点的一半。应急资源配送网络如图1所示,每个需求点的需求量、每条路径的长度和风险值、各应急资源配送中心的建立时间和容量限制如表1、表2和表3所示。
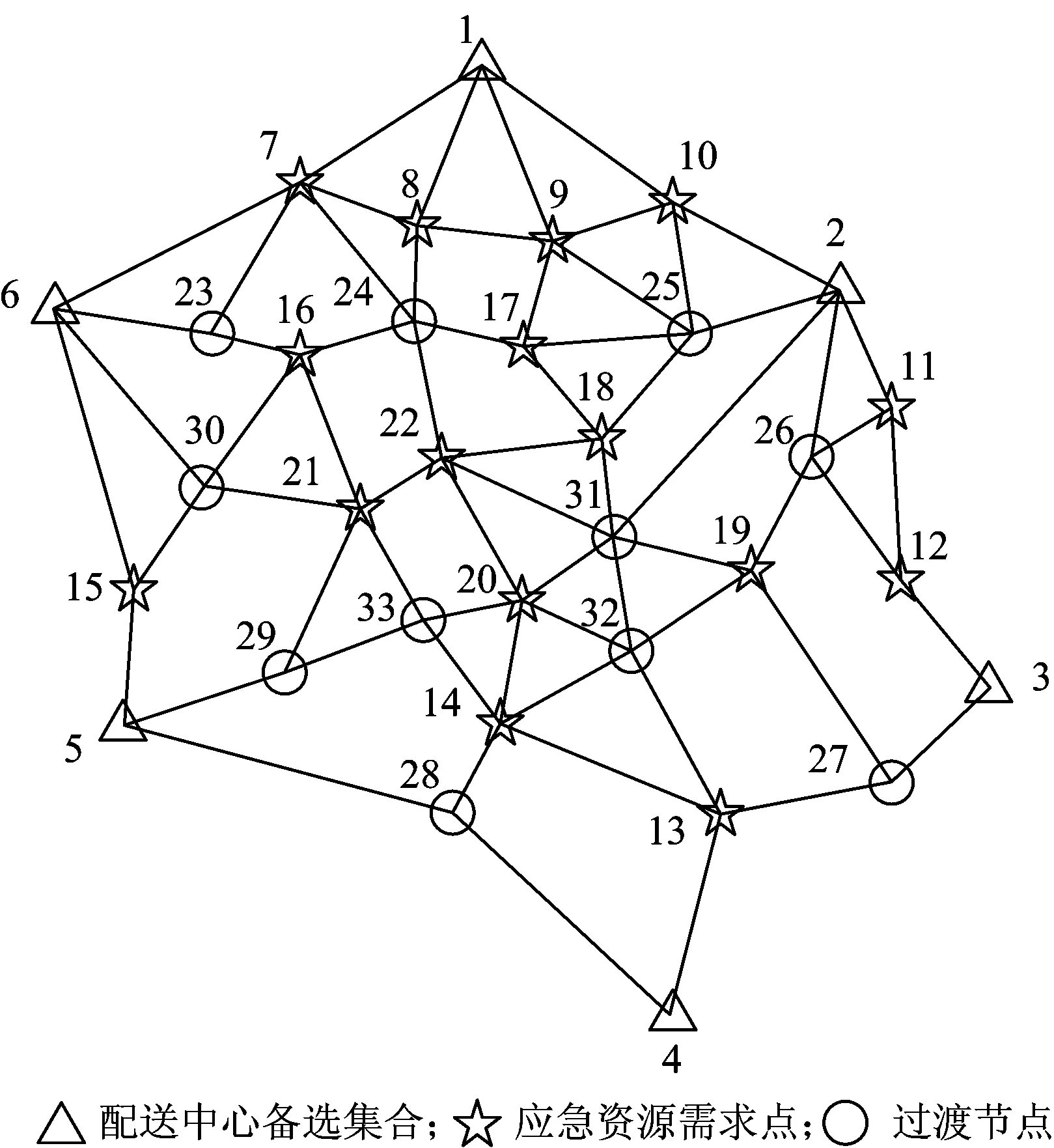
图1 应急资源配送网络Fig.1 Emergency resources distribution network
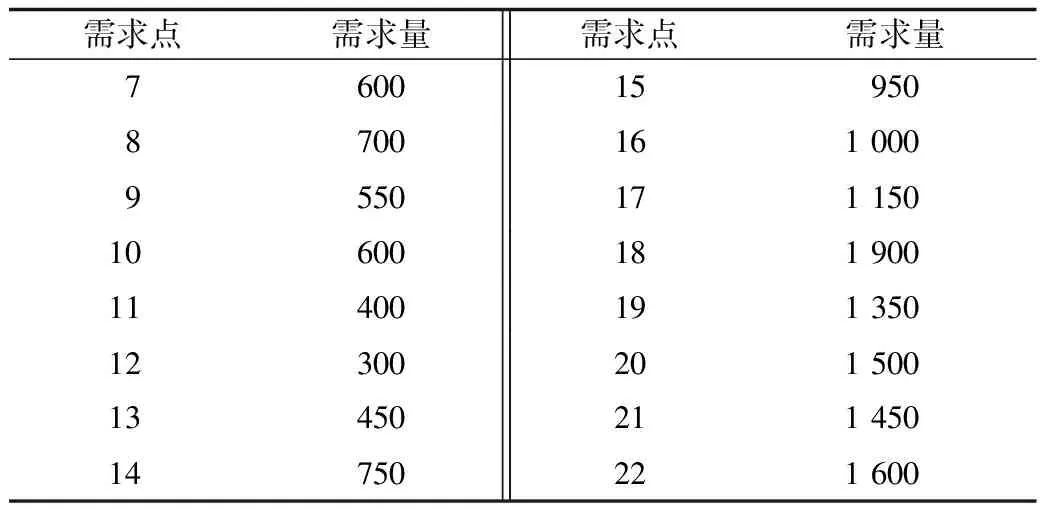
需求点需求量需求点需求量760015950870016100095501711501060018190011400191350123002015001345021145014750221600
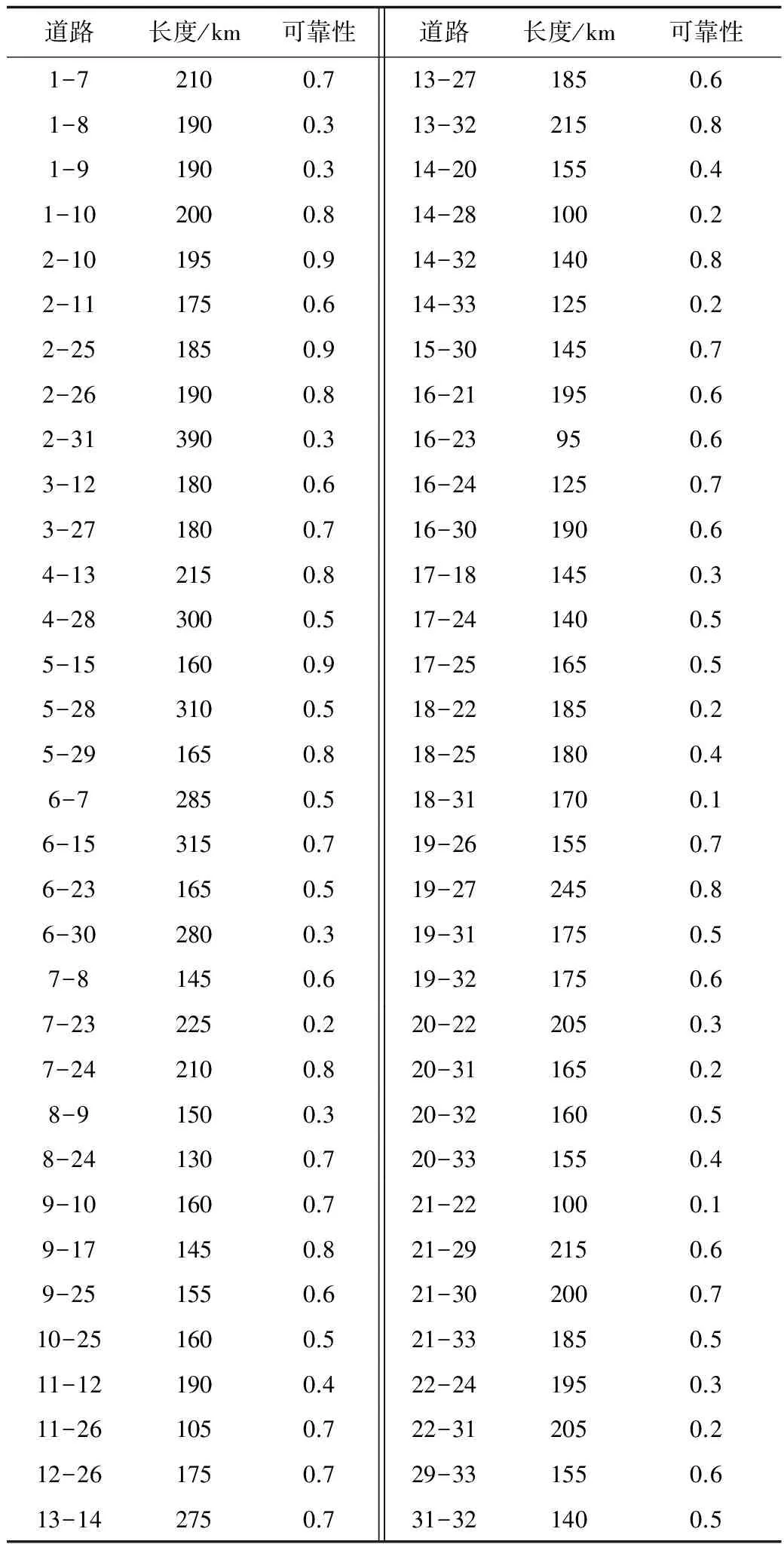
表2 每条路径的长度和通行可靠性数据
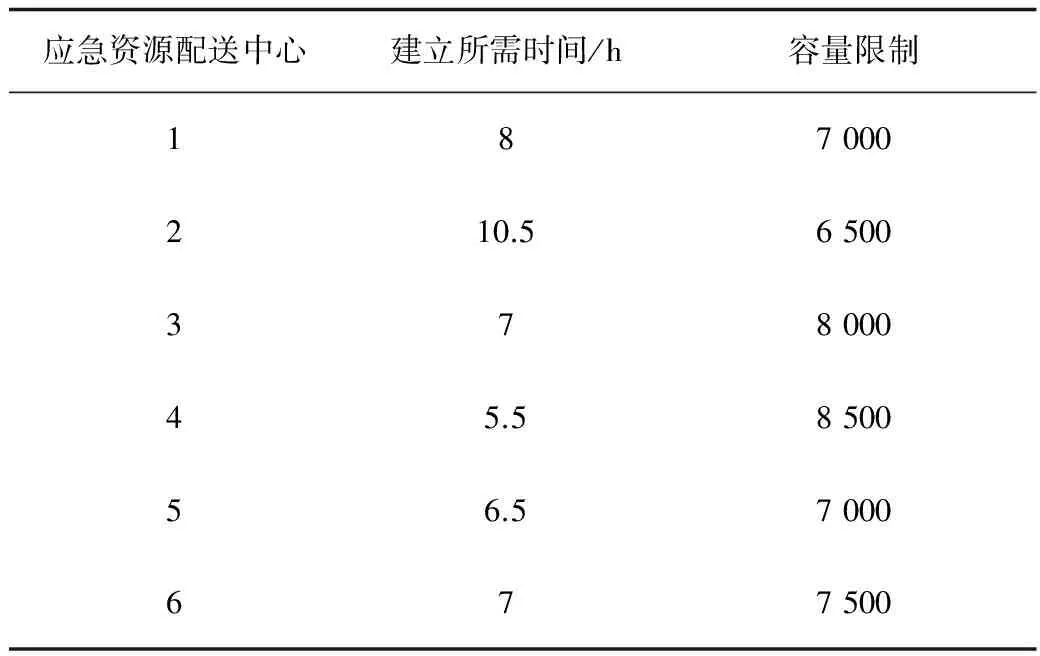
表3 建立各应急资源配送中心所需时间和容量限制
网络图中共计33个点,65条路径。在此交通路网基础上进行优化,进而给出应急资源配送优化方案。在本算例中,我们取车速为70 km/h,VQk为40,在上述路网中通过粒子群算法最终获得的配送方案如表4所示。

表4 应急资源配送方案
配送方案总时间为134.4 h,具体配送方案如图2所示。
研究表明,设计的粒子群算法性能优越,具有较高的运算效率,且能得出较优的解,避免陷入局部最优。对于灾后应急救援来说,该算法适合求解LRP。
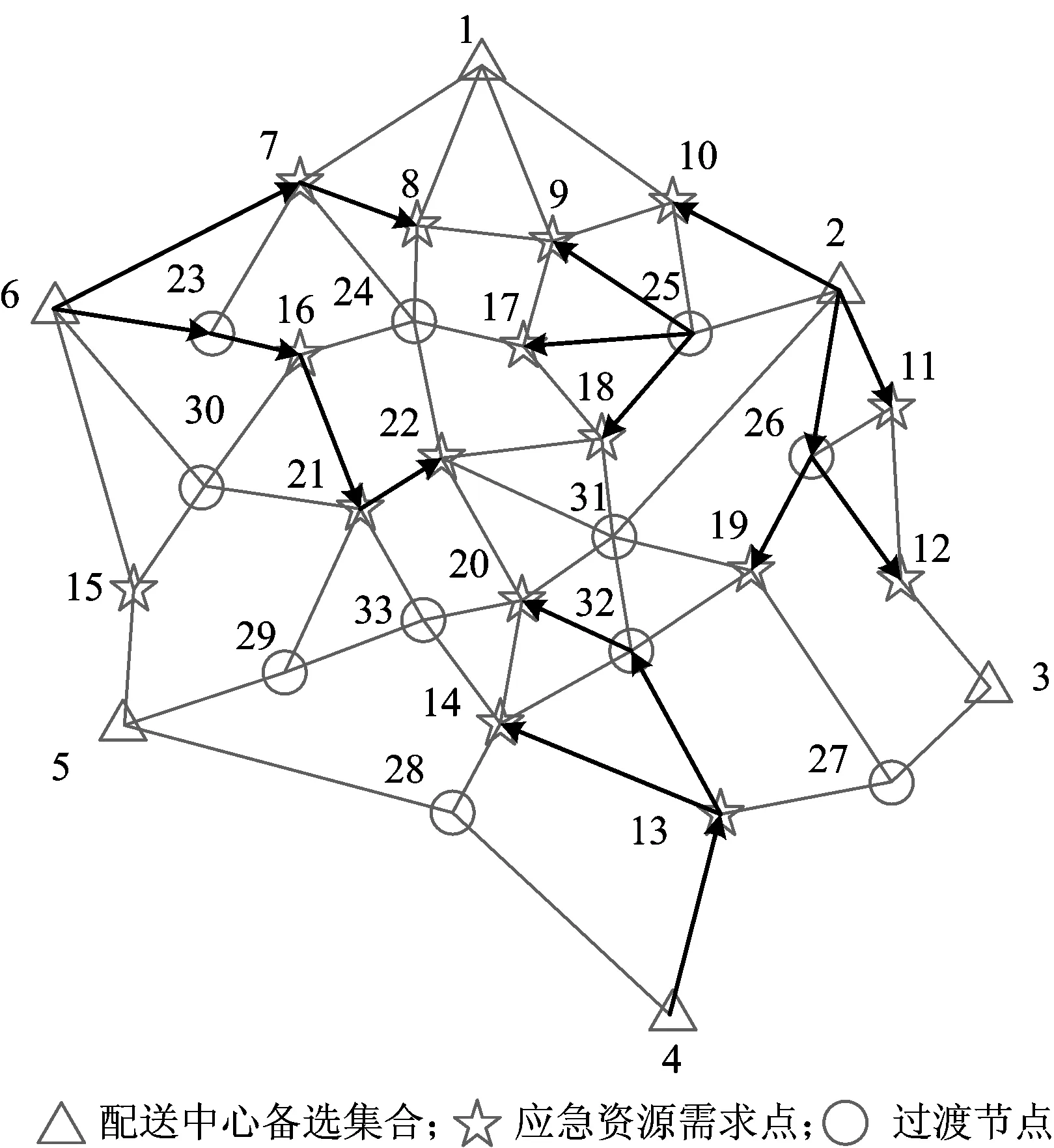
图 2 应急资源配送优化结果Fig.2 Result og Emergency resources distribution plan
4 结论
研究灾后应急资源配送的LRP问题,得出如下结论:
1)引入应急资源配送中心的定位,刻画定位和路网通行可靠性对应急配送方案的影响,以最小化应急救援时间为目标,构建灾后应急资源配送LRP优化模型,给出应急资源配送中心定位与可靠路径选择的全局优化方案。
2)根据模型本身的特点和问题的实际性,设计离散粒子群优化模型算法,并结合仿真与分析,验证模型和算法的有效性,模型与算法的研究对于灾后应急资源的配送决策具有一定指导意义。
3)在实际灾后应急救援过程中,应急资源包括多个种类,不只是单纯的某1类应急资源,此外,灾后部分道路路网的中断也是应急救援需要面临的问题,这些实际救援中需要考虑的因素,也是后续研究的方向之一。
[1]WASTON C, DOHRN P. Depot location with van Salesman-A practical approach[J]. Omega The International Journal of Management Science, 1973, 1(3): 321-329.
[2]W. TAI, Y.L. CHIN, W.B. JIUN. Heuristic Solutions to Multi-depot Location-Routing Problems[J].Computers and Operations Research, 2002, 29:1393-1415.
[3]S. ALUMUR, B. KARA. A new model for the hazardous waste location-routing problem[J]. Computers and Operations Research, 2007, 34:1406-1423.
[4]章海峰,张敏,杨超.一类运输工具带双重能力约束的LRP问题[J].武汉理工大学学报(交通科学与工程版),2006,30(2):220-223.
ZHANG Haifeng, ZHANG Min,YANG Chao. A locatio and routing problem with double vehicle capacity constraints[J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2006, 30(2):220-223.
[5]徐琴,马祖军,李华俊.城市突发公共事件在应急物流中的定位——路径问题研究[J].华中科技大学学报(社会科学版),2008,22(6):36-40.
XU Qin, MA Zujun, LI Huajun. Location-routing problem in emergency logistics for public emergencies[J]. Journal of Huazhong University of Science and Technology(Social Science Edition),2008, 22(6):36-40.
[6]BALCIK B, BEAMON B M, KREJCI C C, et al. Coordination in humanitarian relief chains: Practices, challenges and opportunities[J]. International Journal of Production Economics, 2010, 126(1, SI): 22-34.
[7]JOTSHI A, GONG Qiang, BATTA R. Dispatching and routing of emergency vehicles in disaster mitigation using data fusion[J]. Socio-economic Planning Sciences, 2009, 43(1): 1-24.
[8]ÖZDAMAR L, EKINCI E, KÜÇÜKYAZICI B. Emergency logistics planning in natural disasters[J]. Annals of Operations Research, 2004, 129(1/4): 217-245.
[9]YI Wei, KUMAR A. Ant colony optimization for disaster relief operations[J]. Transportation Research Part E-Logistics and Transportation Review, 2007, 43(6): 660-672.
[10]RAHMAN S U, SMITH D K. Use of location-allocation models in health service development planning in developing nations[J]. European Journal of Operational Research, 2000, 123(3): 437-452.
[11]刘春林,施建军,何建敏.一类应急物资调度的优化模型研究[J].中国管理科学,2001,9(3):29-36.
LIU Chunlin, SHI Jianjun, HE Jianmin. The study on optimal model for a kind of emergency material dispatch problem[J]. Chinese Journal of Management Science, 2001, 9(3): 29-36.
[12]缪成,许维胜,吴启迪.大规模应急救援物资运输模型的构建与求解[J].系统工程,2006,24(11):6-12.
MIAO Cheng, XU Weisheng, WU Qidi. A transportation modal and solution of large-scale emergency relief commodities[J].Systems Engineering,2006, 24(11): 6-12.
[13]应夏晖,孙莉,李锦霞.模糊环境下应急物资配送路径优化研究[J].公路交通科技,2014,31(10):154-158.
YING Xiahui,SUN Li,LI Jinxia. Study on route optimization for emergency supply dispatch in fuzzy environment[J]. Journal of Highway and Transportation Research and Development, 2014,31(10):154-158.
[14]郭崇慧,谷超,江贺.求解旅行商问题的一种改进粒子群算法[J].运筹与管理,2010,19(5):20-26.
GUO Chonghui ,GU Chao ,JIANG He.An improved particle swarm optimization for traveling salesman problem [J].Operations Research and Management Science, 2010,19 (5): 20-26.
