基于突变理论的采空塌陷区输气管道危险性评价研究
2017-04-14姚安林徐涛龙
舒 畅,姚安林,2,徐涛龙,王 惠,秦 朝
(1.西南石油大学 石油与天然气工程学院,四川 成都 610500;2.油气消防四川省重点实验室,四川 成都 610500; 3.中国石油集团工程设计有限责任公司 北京分公司,北京 100085)
0 引言
当人类对地下矿藏进行开采时,覆盖在矿藏上的地层逐渐失去应力支撑,当开采量达到一定的界限,地层原有的力学结构被打破,失去应力平衡。当地层的支撑力不足以抵抗由平衡破坏带来的应力集中时,就会发生应力释放[1],引发采空塌陷。此类危害由于其破坏性与危险性极大,已经成为了威胁管道工程安全的主要危害之一。
由于塌陷区的存在,当铺设的输气管道通过采空区时,将对管道的安全造成巨大威胁。当地下采空后,管道会在地表发生移动破坏的过程中随着地表的沉降而沉降,一旦超过了管道最大变形值,管道就不再随着地表的沉降而沉降,管道的受力将变大,且极有可能发生管道悬空等事故,严重时甚至会发生断管。就西气东输工程而言,它从我国新疆的塔里木轮南油田出发,穿越十个省、区,抵达东方的上海,而在其线路上,不乏大量的煤炭基地,如陕西神府、山西的河东,霍西,沁水、河南焦作、山东兖州、江苏徐州及两淮等煤炭基地,这些地区的煤炭储量超过4万亿t,占据我国探明煤炭储量的九成以上[2]。因此研究采空塌陷区输气管道的危险性评价,不但可以助力我国西气东输战略计划的有效实施,为合理安全地开采矿产资源提供建设性理论依据,还对保证输气管道安全运营有着重要意义。
针对管道安全评价,传统方法有模糊综合评价法[3]、灰色系统理论[4]、神经网络评价[5]等,但这些方法均需人为确定相关指标权重,影响评价结果的客观性。采空塌陷区输气管道安全状态的变化是一个由量变到质变的过程,需要具有较强非线性处理能力的评价模型。突变理论考虑了各评价指标的相对重要性,定性和定量相结合,从而有效降低了人为因素对结果的干扰,使得最终的结果更加客观[6],并在其他领域得到了较好地应用[7-9]。以下将突变理论和综合评价结合起来,建立采空区输气管道危险性评价指标体系,然后根据归一化公式进行量化递归运算,根据最后总的突变级数值,得到采空塌陷区输气管道危险性等级。
1 突变理论
突变理论由法国的数学家雷勒·托姆[10]于上世纪创立,它是研究动态系统在连续发展变化过程中出现的不连续突变现象及其与连续变化因素之间关系的数学理论。在实际中,很多研究对象的变化并不是呈现出一定的连续状态,而是在某一临界点突然表现出某一状态,于是在综合拓扑动力学与奇点理论的观点后,突变理论通过建立势函数来表征研究对象的变化状态,利用这一函数区分研究对象发生变化的临界点,进而具体分析临界点左右的间断性变化,最后得出初等突变模型[11]。
一般根据表征状态的不同将势函数中的变量划分为2种,其一是状态变量,主要表征研究对象自身的行为状态;其二是控制变量,用来表征左右变量变化的因素。设势函数为f(x),对其求导,并使得一阶导数f′(x)=0,得到它的平衡曲面,使二阶导数f″(x)=0解得平衡曲面的奇数点集,将以上2个式子联立、化简,得到只有控制变量的分歧方程,当控制变量变化到使得方程成立的时候,就是研究对象发生突变的时候,进而就能够获取每个控制变量引起突变的临界点[11]。
以下选取了4个比较典型的初等突变模型,相应的公式在表1中详细列出。

表1 4种基本突变模型形式[12]
2 基于突变理论的采空塌陷区输气管道危险性评价模型构建
2.1 采空塌陷区输气管道危险性评价指标体系
影响采空塌陷区输气管道危险性的因素很多,既包含定量因素,又包含定性因素,而且不同因素之间并非完全独立,它们会不断产生相互作用,因此,在选取指标时,应该优先考虑能以最少量度反映最多信息的指标。参考文献[13]和[14],综合考虑采矿因素、岩体物理力学参数、环境与地质因素和埋地管道因素等4个方面,选取14项评判指标,建立采空塌陷区输气管道危险性评价指标体系,如图1所示。
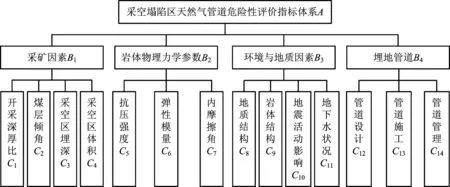
图1 采空塌陷区输气管道危险性评价指标体系Fig.1 Hazard index system of natural gas pipeline in the mining subsidence area
2.2 定性因素评价指标分级标准
依照危险性系数的高低,将采空塌陷区管道危险性划分为以下4个档次。参考文献[15],建立采空塌陷区输气管道危险性定性因素评价指标分级标准,如表2所示。
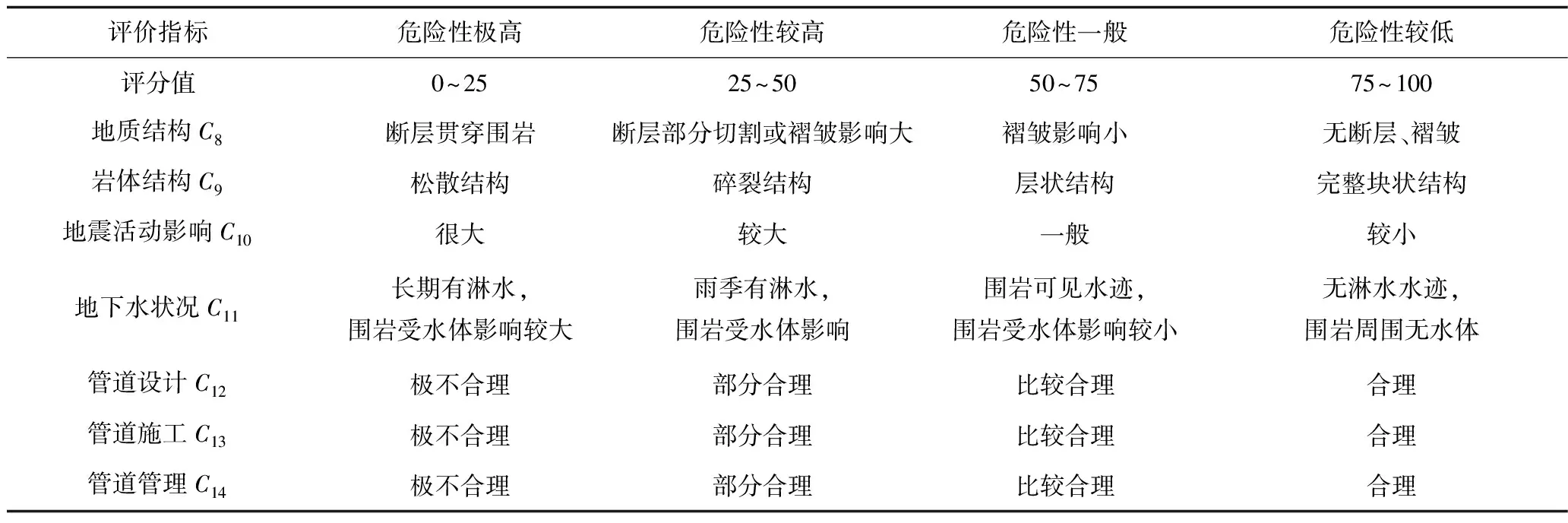
表2 定性因素评价指标分级标准
2.3 数据无量纲化处理
在已建立的评价体系中,各评价指标往往具有不同的量纲和量纲单位,彼此之间无法进行比较,因此运用极差变换法,对评价指标进行无量纲化处理[14]。
1)对于指标越大越好型:
(1)
2)对于指标越小越好型:
(2)
式中:yij为无量纲处理后的值;xij为原始数据;xmax(j)为j行数据中的最大值;xmin(j)为j行数据中的最小值。若控制变量已是[0,1],则无需进行无量纲化处理。
2.4 基于突变理论的评价规则
依据不同的突变类型,使用表1中对应的归一化公式进行数据处理,分级求得隶属度值,并进行递归运算求得总隶属函数值。多目标突变评价一般遵循以下规则[12]:
1)互补性规则。系统中,控制变量(如a,b,c和d)彼此可以替代或弥补不足时,状态变量按照控制变量的平均值取用。即:
(3)
2)非互补性原则。系统中,控制变量(如a,b,c和d)彼此不能代替或弥补不足时,状态变量按照控制变量的最小值取用。即:
x=min{xa,xb,xc,xd}
(4)
2.5 评价等级及意义
在对采空塌陷区输气管道危险性评价的突变模型的分析及其主要因素识别的基础上,结合相关专家的意见,设定采空塌陷区输气管道危险性评价标准,如表3所示。

表3 采空塌陷区输气管道危险性评价标准
2.6 综合评价分析
基于突变理论的归一化公式对上述获得的隶属函数值进行量化递归计算,获得底层指标的突变级数值,依据评价决策准则,逐层计算各级指标的突变级数值,直至得到系统总的突变隶属函数值,即可确定采空塌陷区输气管道危险性程度。
3 实例分析
以我国山西境内通过采空塌陷区的输气管道为例,管线钢级为X70,外径为1 016 mm,壁厚为20 mm,管道设计压力为10 MPa,各管段所处地理位置不同。采用上述评估模型对该输气管道的5个处于不同采空塌陷区的管段进行危险性评价。
3.1 指标的评价分值
根据图1所示采空塌陷区输气管道危险性评价指标体系,邀请5名管道安全和地质工程方面的专家组成评价小组,结合实际对定量指标直接赋值,对定性指标根据表2进行分值评估,然后求其算术平均值。评价小组专家对这5段管道各项指标进行评价的结果如表4所示。
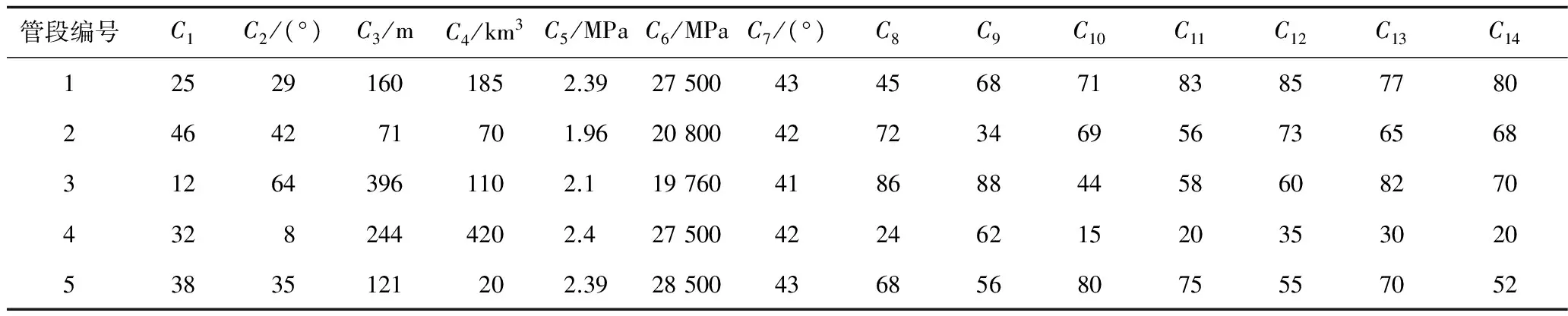
表4 指标的评价分值
3.2 各管段危险性评价
对上表中的各个因素实施无量纲化处理,由于采空区的体积和煤层倾角这2个指标值越小,对危险性的影响越小,因此应使用式(2)进行数据处理,其余的指标则是值越大,引起的危险性越小,所以应使用式(1)进行处理,最终的结果在表5中详细列出。
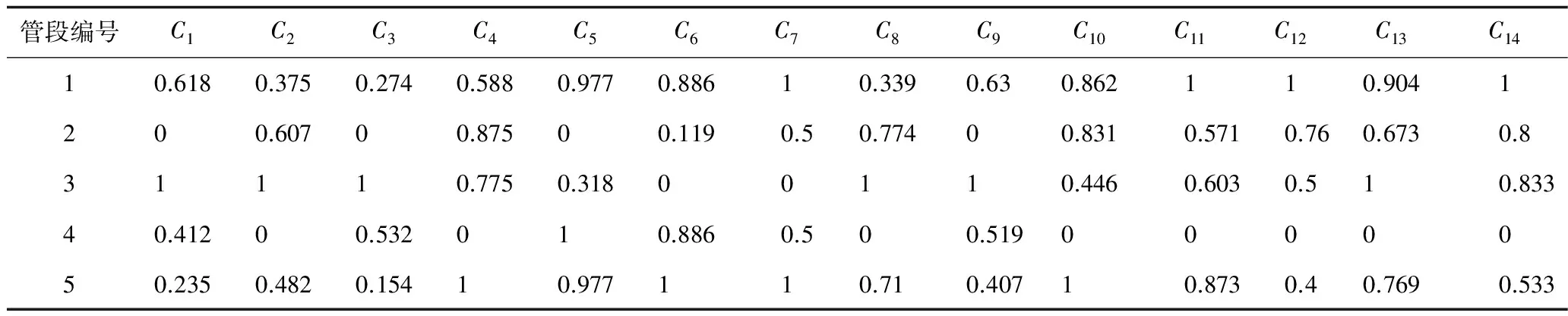
表5 无量纲化后的最底层指标数据
由指标体系可知,构成蝴蝶突变模型的有:C1,C2,C3,C4和B1;C8,C9,C10,C11和B3;B1,B2,B3,B4和A。构成燕尾突变模型的有:C5,C6,C7和B2;C12,C13,C14和B4。可运用表1中公式求出归一化后的最底层指标值。以管段1中指标体系采矿因素B1为例,其具体计算过程为:由表5可知二级指标C1,C2,C3,C4的无量纲化值分
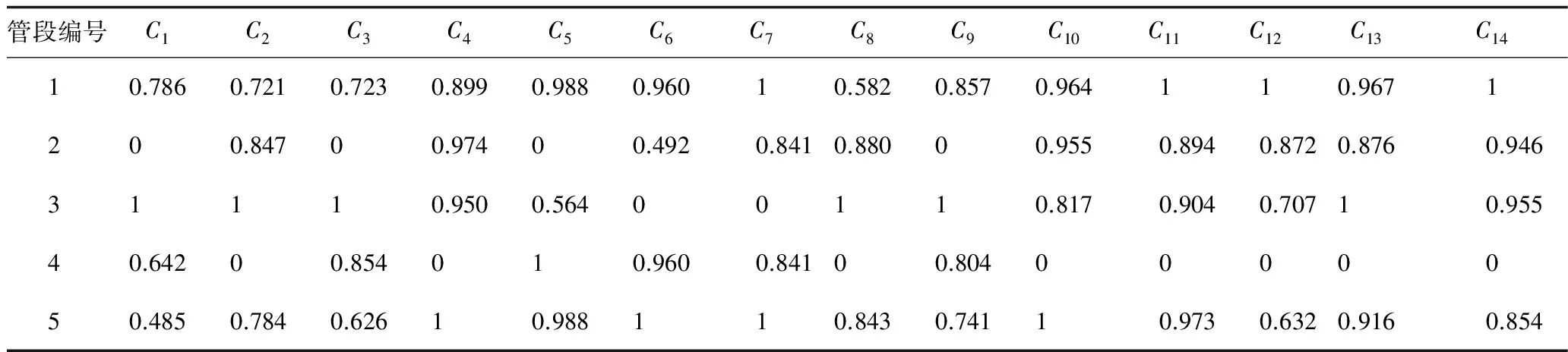
表6 归一化后的最底层指标值
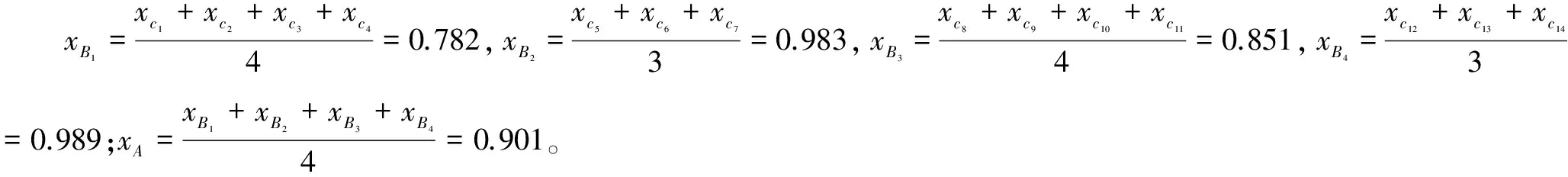
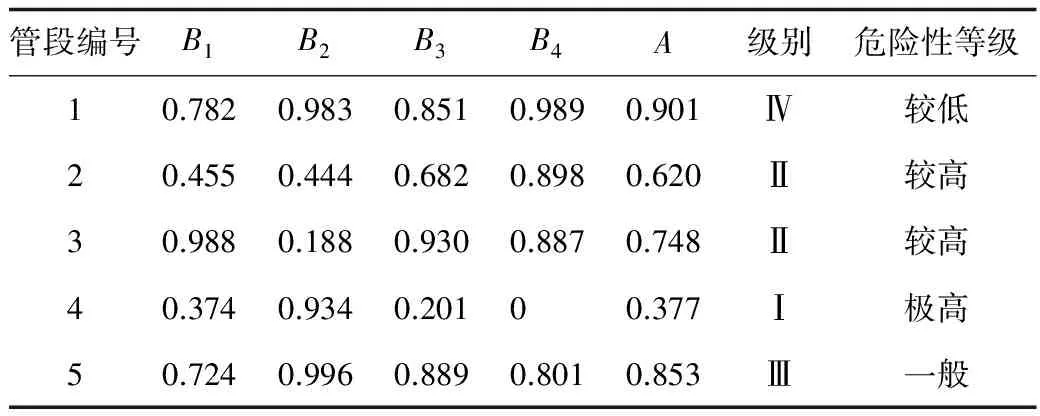
表7 5段管段的突变级数值及危险性等级
3.3 评价方法的比较
基于突变理论对5段采空塌陷区管道进行危险性评价,同时采用输气管道环境及地质灾害风险评估软件[16]对上述5段管道进行失效可能性评价,其中,输气管道环境及地质灾害风险评估软件采用半定量评价方法,将失效可能性分为高、中等和低3个级别,评价结果如表8所示。
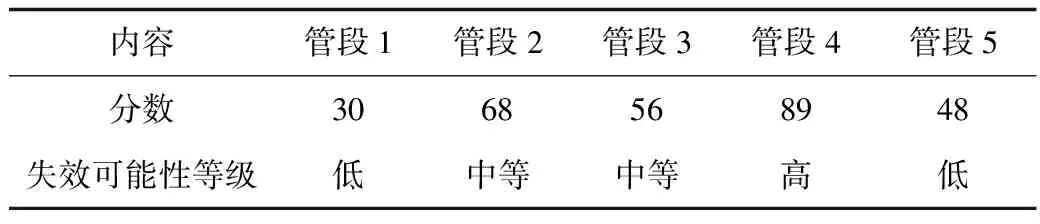
表8 基于评估软件的各管段失效可能性评估结果
3.4 分析与讨论
1)从表7可以看出,各段采空塌陷区输气管道的总突变级数分别为0.901,0.620,0.748,0.377和0.853,管段4失效可能性等级属于Ⅰ级,危险性等级为极高;管段2和管段3失效可能性等级属于Ⅱ级,危险性等级为较高;管段5失效可能性等级属于Ⅲ级,危险性等级为一般;管段1失效可能性等级属于Ⅳ级,危险性为较低。评价结果与采用输气管道环境及地质灾害风险评估软件对采空塌陷区输气管道失效可能性评价结果基本相符。
2)由以上数据可知,管段2中xB2=0.444,xB3=0.682,影响管段2安全的主要因素为岩体物理力学参数和环境与地质因素;管段3中xB2=0.188,影响管段3安全的主要因素为岩体物理力学参数;管段4中xB1=0.374,xB3=0.201,xB4=0,影响管段4安全的主要因素为采矿因素、岩体物理力学参数和环境与地质因素采空区体积和抗压强度等。对以上3段管道的危险性应高度重视,加强监督。
3)由以上数据可知,管段5的危险性一般,但管段5中xB1=0.724,xB4=0.801,表明采矿因素处于危险性较高等级,而埋地管道因素处于临界等级,且只比该等级的下端临界点(0.8)高0.01,应及时采取改进完善措施。
4 结论
1)通过对影响采空塌陷区输气管道危险性的因素分析,建立了以突变理论为基础的评价模型。该模型考虑采矿因素、岩体物理力学参数、环境与地质因素和埋地管道因素等4个方面,共14个定性和定量指标,对定量指标采用实际测量的方法确定指标特征值,定性指标采用多位专家根据实际情况赋分求其平均值的方式确定,实现了定性和定量指标量化标准的统一。
2)采用突变理论建立采空塌陷区输气管道危险性评价模型,该模型避免了人为制定权重,在一定程度上降低了一般评价法中蕴含的主观性,使评价结果更加客观公正,易于被评价单位所接受,同时也简化了数据处理过程,计算量小,简单易行。
3)所建立的基于突变理论的采空塌陷区输气管道危险性评价模型进行了实例应用,其评价结果与采用输气管道环境及地质灾害风险评估软件对采空塌陷区输气管道失效可能性评价结果基本一致,表明方法可行。在该评价结果的基础上,可科学制定相应的风险防控措施。
[1]马海涛,贺红生,付士根.采空塌陷影响因素及稳定性分级方法研究[J].中国安全生产科学技术, 2008,4(5):37-41.
MA Haitao,HE Hongsheng,FU Shigen. Study on factors and classifying method of goafstability[J].Journal of Safety Science and Technology,2008,4(5):37-41.
[2]张和生. 山区地下开采引起地表变形对长输管线的影响研究[D]. 太原: 太原理工大学, 2013.
[3]徐涛龙,姚安林,蒋宏业.基于模糊综合评价的城市燃气管网第三方破坏失效可能性研究[J].中国安全科学学报,2010,20(8):166-169.
XU Taolong, YAO Anlin, JIANG Hongye. Study on failure possibility of third-party damage to urban gas pipeline network based on fuzzy comprehensive evaluation[J]. China Safety Science Journal, 2010,20(8):166-169.
[4]徐涛龙,姚安林,曾祥国,等. 基于灰色关联分析的LNG接收终端人因事故辨识方法[J].中国安全生产科学技术,2011,7(9):97-101.
XU Taolong, YAO Anlin, ZENG Xiangguo, et al. Human accidents identification method of LNG receiving terminal based on grey relational analysis [J]. Journal of Safety Science and Technology,2011,7(9):97-101.
[5]张锦伟,姚安林,杨璐,等. 基于风险的输气站场设施检测周期确定方法研究[J]. 中国安全科学学报, 2013,23(4):167-171.
ZHANG Jinwei, YAO Anlin, YANG Lu, et al. Research on method for determining of gas transmission station facilities detection cycle based on risk[J]. China Safety Science Journal, 2013, 23(4):167-171.
[6]刘聚涛,高俊峰,姜加虎,等.基于突变理论的太湖蓝藻水华危险性分区评价[J].湖泊科学,2010,22(4):488-494.
LIU Jutao,GAO Junfeng,JIANG Jiahu,et al. Catastrophe theory-based risk evaluation of blue-green algae bloom of different regions in Lake Taihu[J]. Lake Sci,2010,22(4):488-494.
[7]曾跃辉,姚安林,吴瑶晗,等. 基于突变理论的油库事故应急救援能力评价方法研究[J]. 中国安全科学学报, 2016,26(4):84-89.
ZENG Yuehui, YAO Anlin, WU Yaohan, et al. Study on based catastrophe theory method of assessing emergency rescue capability for oil depot accidents[J]. China Safety Science Journal, 2016,26(4):84-89.
[8]徐亚博,葛悦,王培怡,等. 基于突变理论的地铁安全模糊动态评价[J]. 安全与环境学报, 2014,14(6):11-14.
XU Yabo, GE Yue, WANG Peiyi, et al. Assessment research on the fuzzy dynamic safety for subway system based on the mutation theory [J]. Journal of Safety Science and Environment, 2014,14(6):11-14.
[9]陈红江,彭小兰. 突变级数法在电站燃煤锅炉结渣预测中的应用 [J].中国安全生产科学技术, 2014,10(8):97-102.
CHEN Hongjiang, PENG Xiaolan. Application of catastrophe progression method in forecasting slagging of coal-fired boiler[J]. Journal of Safety Science and Technology, 2014, 10(8):97-102.
[10]雷勒托姆.突变论:思想及运用[M].周仲良译.上海:上海译文出版社, 1989.
[11]凌复华. 突变理论及其应用[M].上海: 上海交通大学出版社, 1987.
[12]李春辉,方菊明,何泽军,等. 基于突变理论的建筑企业安全管理评价研究[J]. 中国安全生产科学技术,2011,7(12):87-91.
LI Chunhui, FANG Juming, HE Zejun, et al. Research of safety management evaluation based on catastrophe theory in construction companies[J]. Journal of Safety Science and Technology, 2011,7(12):87-91.
[13]康乐. 煤矿采空区管道安全评估方法研究[D]. 成都: 西南石油大学, 2014.
[14]陈娇,罗周全,侯造水. 基于改进突变级数法的金属矿采空区稳定性评价[J]. 中国安全生产科学技术, 2013,9(11):17-24.
CHEN Jiao, LUO Zhouquan,HOU Zaoshui. Stability evaluation of metal mine goaf based on improved catastrophe progression method[J]. Journal of Safety Science and Technology, 2013, 9(11):17-24.
[15]李孜军,林武清,陈阳.基于AGA-BP神经网络的采空区危险性评价[J]. 中国安全生产科学技术,2015,11(7):135-141.
LI Zijun, LIN Wuqing, CHEN Yang. Evaluation on risk of goaf based on AGA-BP neural network[J]. Journal of Safety Science and Technology, 2015,11(7):135-141.
[16]西南石油大学. 输气管道环境及地质灾害风险评估软件V1.0:2011SR084090[CP].2011-11-18.
