运用量纲分析探究爆炸应力波在中远区岩石中的衰减规律*

赵东寅

(紫金矿业集团股份有限公司，福建 上杭 364200)

数字出版日期： 2017-01-13

0　引言

岩体爆破是大型水利、采矿工程开挖必不可少的施工手段[1]。为了不断改进工程爆破的设计参数、工艺及技术，以达到理想的爆破效果，对爆炸应力波在中远区岩石中衰减规律的研究依然任重而道远。炸药在岩石中爆炸后，形成向四周传播的冲击波，在高温、高压和高速冲击波的作用下，炮源中心岩层介质产生巨大扰动并伴随应力的突然跃升，同时带动相邻质点的扰动，引起质点之间的应力作用。随着传播距离的增加，应力逐渐衰减，冲击波衰减为应力波、地震波，用常数项为负数的幂函数可以大致地描述应力波衰减的这一历程。

国内外学者对纵观岩石爆炸应力波衰减规律的研究，主要通过大量的工程数据整理分析，总结经验公式，或通过物理力学方程推导应力波的衰减公式，再借助实测数据或模拟实验来验证公式的准确性。比如褚怀保[2]等人通过断裂损伤理论分析了煤体中爆炸应力波作用机理及应力波作用下岩石的损伤断裂准则，根据有效应力原理得出煤体所受有效应力的衰减公式，并设计了应力波测试实验进行验证。曹攀[3]等人通过分析岩石爆炸反射波和折射波状态参数及岩石中的动态应力场得出应力峰值衰减公式，建立岩体UDEC数值模型模拟不同距离岩体质点的应力特征，从而验证理论公式的合理性；K. O. Hakalehto[4]通过岩石应力杆试验，总结得出岩石中平面应力波的衰减公式。我国武汉岩土力学研究所通过现场试验测得应力波衰减指数，并参照John S Rinehart提出的冲击波衰减规律来研究应力波衰减特征[5-6]。此外，李彰明[7]，史晓鹏[8]，Sun Wei[9]，王明洋&钱七虎[10]，孙冰[11]等人也在岩石爆炸应力波衰减规律方面做了大量的研究工作。

钱学森先生认为，爆炸是一个很复杂的能量转换过程，在这一过程中炸药的爆轰和岩石破碎都是在极短的时间内完成，用力学基本原理很难构筑爆炸力学理论，可以用量纲分析方法帮助解决[12]。基于此，与其他应力波衰减规律的研究方法不同，本文运用量纲分析方法，综合考虑炸药量、炸药性能、岩层介质参数等因素对应力传播的影响，构建应力与控制参数的函数表达式，并进行无量纲化，得到爆炸应力波在中远区岩石中的一般衰减规律模型。以青海威斯特基础地质数据为背景，借助LS-DYNA大型动力有限元程序建立数值模型，并针对数值模拟得到的应力监测数据，由数据分布规律确定应力波衰减公式，同时，为验证衰减公式的可靠性，对应力监测数据进行衰减公式拟合。通过本文的分析工作，以期为今后开展爆炸应力波在中远区岩石中的传播规律研究提供参考。

1　量纲分析法推导一般衰减公式

1.1　理论基础

量纲分析方法在爆炸领域运用的主要依据是Π定理和爆炸相似律。其中，Π定理又是量纲分析的理论核心，其内容可以简要概述如下：若某类物理问题涉及n个影响量(自变量)a1，a2，…，an，那么反映该问题的因变量a可以表示为这些自变量的函数：

a=f(a1,a2,…,ak,…,an)

(1)

假设a1，a2，…，ak是具有独立量纲的k个基本量，其量纲分别为A1，A2，…，Ak，那么其余的(n-k)个自变量ak+1，ak+2，…，an以及因变量a都可以由这些基本量导出，其量纲可用基本量量纲的幂次式表示，即：

[ak + 1] =A1p1A2p2…Akpk

(2)

[ak + 2] =A1q1A2q2…Akqk

(3)

……

[an] =A1r1A2r2…Akrk

(4)

[a] =A1m1A2m2…Akmk

(5)

将函数关系式(1)中的各量进行无量纲化，得到量值都是无量纲的纯数，满足的函数关系是：

a/(a1m1a2m2…akmk)=f(1,1,…;ak + 1/(a1p1a2p2…akpk),…,an/(a1r1a2r2…akrk))

(6)

对于式(6)，将左端因变量记为Π，而右端函数中的前k个量都是1，对因变量Π不起作用，后(n-k)个起作用的自变量分别记为Π1，Π2，Πn-k，则函数关系可表示为：

Π=f(Π1,Π2,…,Πn-k)

(7)

在式(7)的基础上，遵循相似规律，即让模型(m)和原型(p)的自变量分别对应相等，即：

(Πi)m=(Πi)p(i=1,2,…,n-k)

(8)

就能保证模型和原型的因变量也相等，即有：

(Π)m=(Π)p

(9)

在解决实际问题时，应把握问题的物理实质，全面比较各个自变量对因变量所起的作用，合理舍弃作用较小的自变量，从而得到一个较简便的关系式。对于所得的一般关系式，还需通过模型实验或数值模拟来确定函数的具体形式，并对其进行合理的试探和修正。

1.2　推导过程

对于炸药爆炸产生的应力波在中远区岩体的传播过程，可视炸药具有流体性质，视岩石具有弹塑性固体性质。描述炸药流体性质的状态量，本文选用JWL状态方程：

(10)

上述方程的控制参数包括：A，B，R1，R2，ω，其具体含义、单位及量纲，如表1所示。

描述岩石弹塑性固体性质的状态量，可分别选用弹性胡克定律、Von Mises屈服准则、Prandtl-Reuss关系来描述岩石在应力波作用下的弹性阶段、屈服阶段和塑性阶段三个过程[13-15]。在这些模型中，控制参数包括：弹性常数E、v，屈服极限Y，其具体含义、单位及量纲，如表1所示。

综合考虑炸药量、装药密度、单位炸药释放量以及岩石初始密度等因素，得到影响爆炸应力波强度的控制参数及其符号、单位以及在L-M-T量纲系统中的量纲，如表1所示。

于是，用上述控制参数表示的应力波函数为：

σ=f(Q,ρe,γe,Ee,A,B,R1,R2,ω;ρr,E,v,Y,R)

(11)

选取Q，Ee，ρe作为基本量，对式(11)进行无量纲化，有：

(12)

表1　应力波强度影响因素参数

对于给定的炸药和岩石材料，有：

(ρe,γe,Ee,A,B,R1,R2,ω;ρr,E,v,Y)=const

(13)

因此，可以忽略上述参数对爆炸应力波强度的影响，所以式(12)可以简化为：

(14)

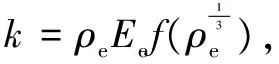
(15)

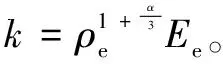
式(15)与公知的萨道夫斯基公式类似，两者主要的区别在于k和α取值的不同，前者主要与炸药性质相关，后者主要与岩石性质相关。

2　数值模拟

模拟过程采用ANSYS/LS-DYNA数值模拟软件，建立以青海威斯特德尔尼露天铜矿边坡为背景的双台阶模型。该矿区边坡岩体以蛇纹岩为主，台阶高度为12 m，边坡角为65°。具体岩石物理力学参数，如表2所示。

表2　岩石材料物理力学参数

模拟过程采用单孔爆破，炮孔参数采用矿区现用爆破参数，其中炮孔直径为80 mm，孔深为13.5 m，炮孔与坡脚水平间距为3 m。装药结构采用孔口堵塞3.5 m，上部装药3.5 m，中间空气间隔1.5 m，底部装药5 m的轴向不耦合装药方式，如图1所示。为方便建模，模拟过程将炮孔按垂直型炮孔布置。炸药使用2号岩石乳化炸药，起爆方法为上下部装药同段反向起爆，炸药相关参数，如表3所示。

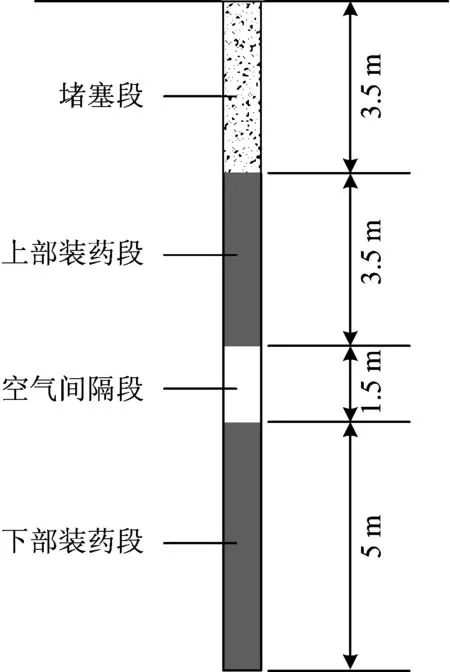
图1　装药结构示意Fig.1　Chart of charging construction

密度/(kg·m-3)爆速/(m·s-1)查普曼-儒盖压强/GPaA/GPaB/GPaR1R2ωE0/GPaV0120032002747．60．5293．50．160．414．51．0

在设置边界条件约束时，台阶模型顶面设为自由面，其他5个面均设为无反射边界条件，设置情况如图2所示。设置完成后，运用LS-DYNA所附带的LS-PrePost后处理程序进行求解运算。

3　数值模拟结果分析

为分析爆炸应力波在中远区岩石中随距离增加的衰减规律，应在同一高程上进行应力波数据分析。对求解后的台阶模型在同一水平选取一系列相邻监测点(相邻监测点之间的距离为单元的尺寸，即1 m)，所取监测点均位于爆炸中远区范围内，如图3所示。同时输出所选19个监测点X方向的应力时程曲线图，如图4所示。对于应力时程曲线图，提取各监测点的应力峰值，并对应监测点距爆源的水平距离，整理得到监测点离爆源距离与应力峰值的对应关系，如表4所示。

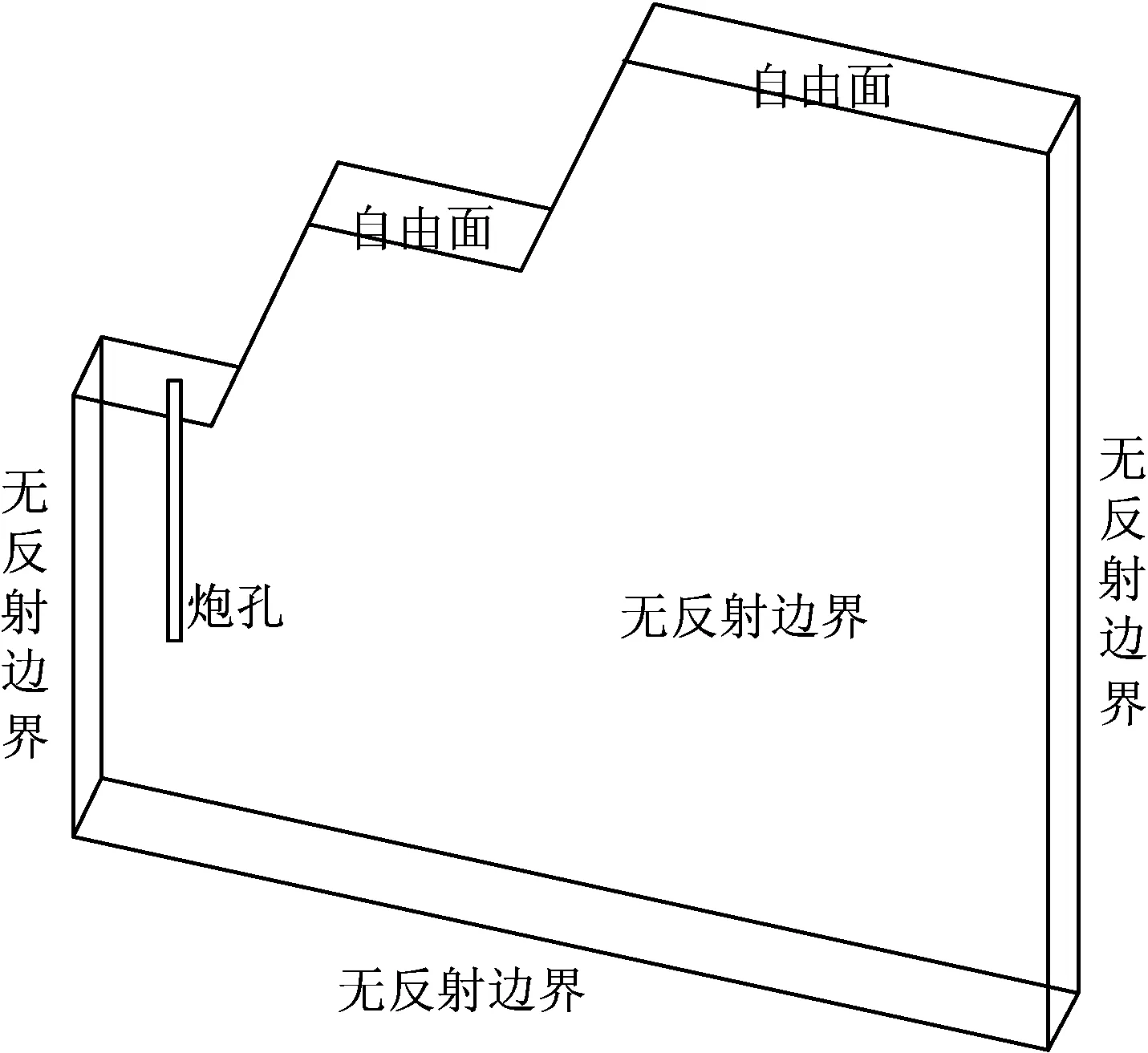
图2　双台阶数值计算模型Fig.2　Numerical calculation model of double slopes

图3　监测点布置图及测点编号Fig.3　Positions of monitoring points and its numbers

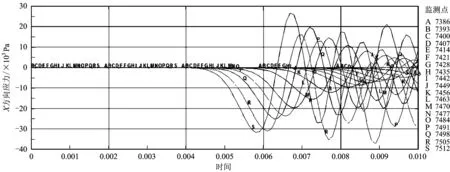
图4　X方向应力时程曲线Fig.4　Process curve of X-axis stress

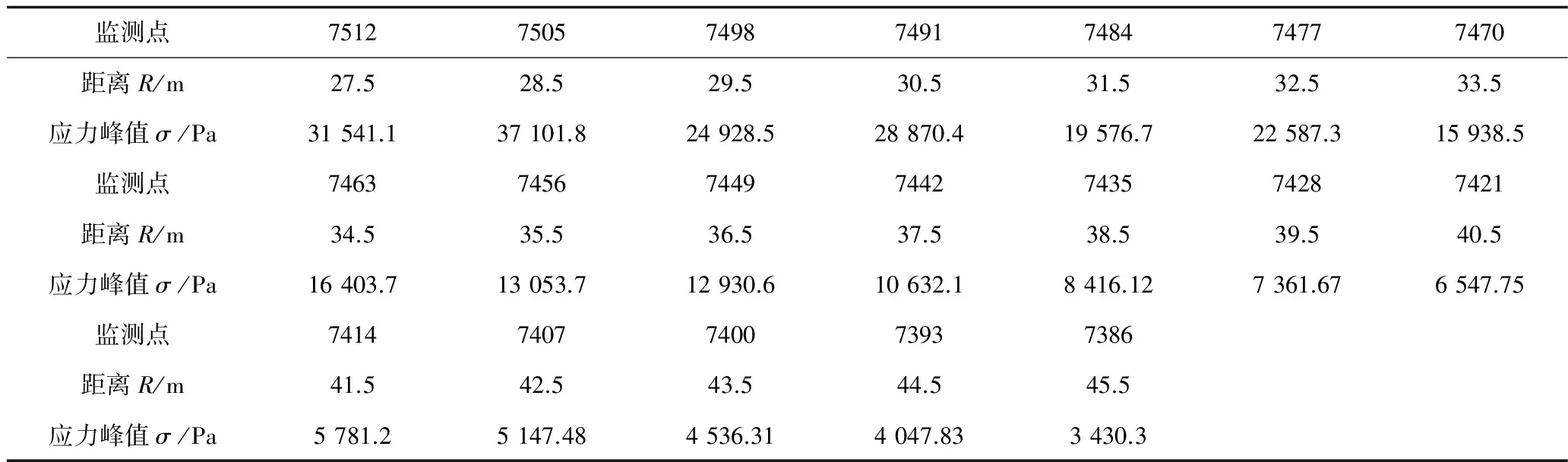
监测点7512750574987491748474777470距离R/m27．528．529．530．531．532．533．5应力峰值σ/Pa31541．137101．824928．528870．419576．722587．315938．5监测点7463745674497442743574287421距离R/m34．535．536．537．538．539．540．5应力峰值σ/Pa16403．713053．712930．610632．18416．127361．676547．75监测点74147407740073937386距离R/m41．542．543．544．545．5应力峰值σ/Pa5781．25147．484536．314047．833430．3

将表4数据，用Origin9.0绘出监测点应力峰值随爆心距的变化规律，如图5所示。从数据点分布可以看出，随着爆心距的增大，应力峰值整体呈衰减趋势，且前半段衰减趋势明显，后半段衰减趋势逐渐减缓。这一衰减规律基本符合常数项为负数的幂函数形式的衰减规律，与引言所述衰减特征基本一致，说明模拟效果能较好地反映实际情况。

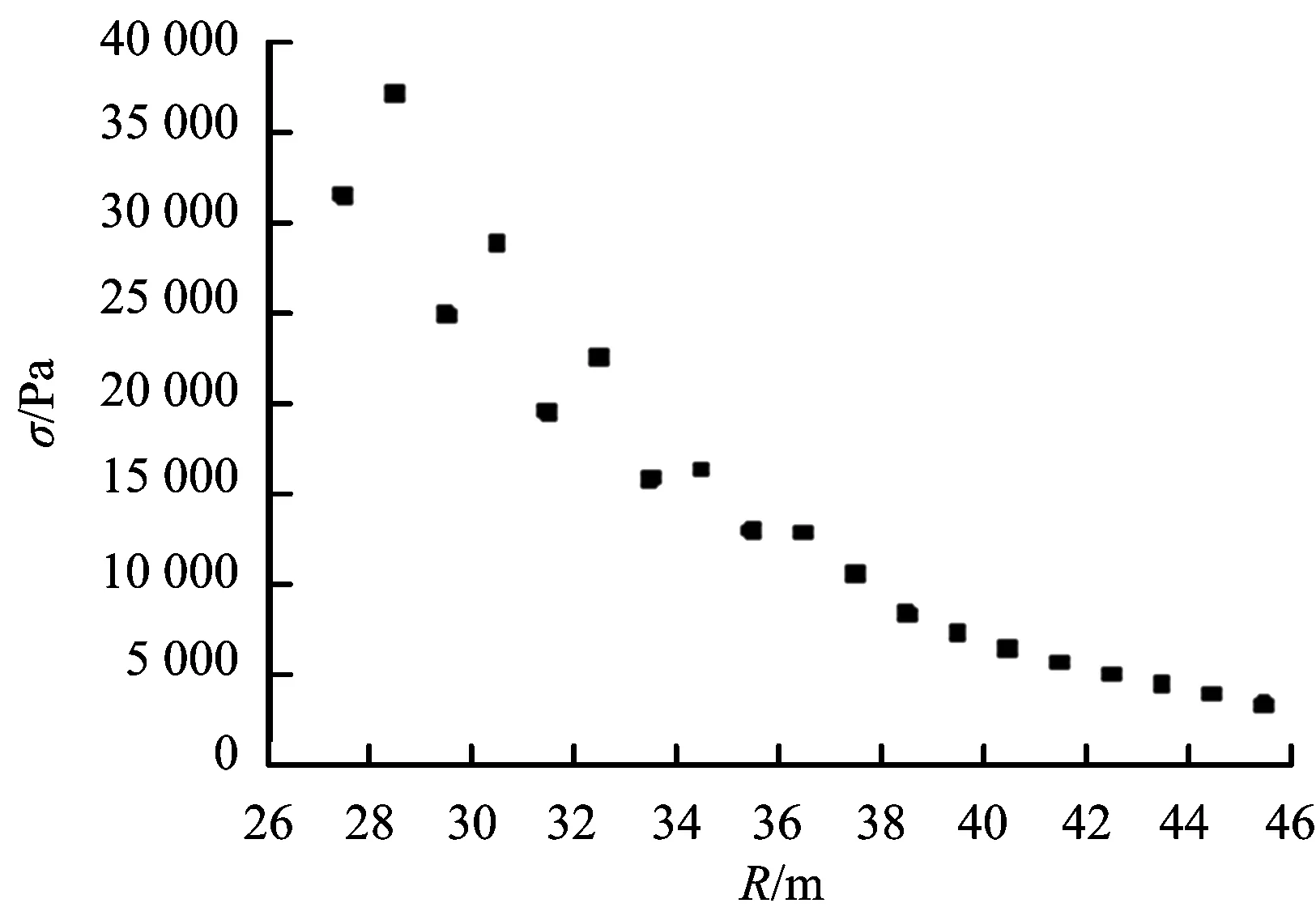
图5　应力峰值随距离衰减规律Fig.5　Peak stress attenuation law with the distance

为进一步探究爆炸应力波在岩石中的具体衰减规律，对式(15)两边同时取对数得：

(16)

在式(16)的基础上，将表4数据中监测点的应力峰值及其对应的爆心距分别取对数，得到lnσ及lnR数据，在Origin9.0环境下，绘出lnσ-lnR关系图，如图6所示。从图中可知，lnσ与lnR基本成线性关系，其拟合关系曲线为图6所示直线，运用多元线性回归方法(Multiple Regression)进行回归分析，可得该直线的对应参数如表5所示。

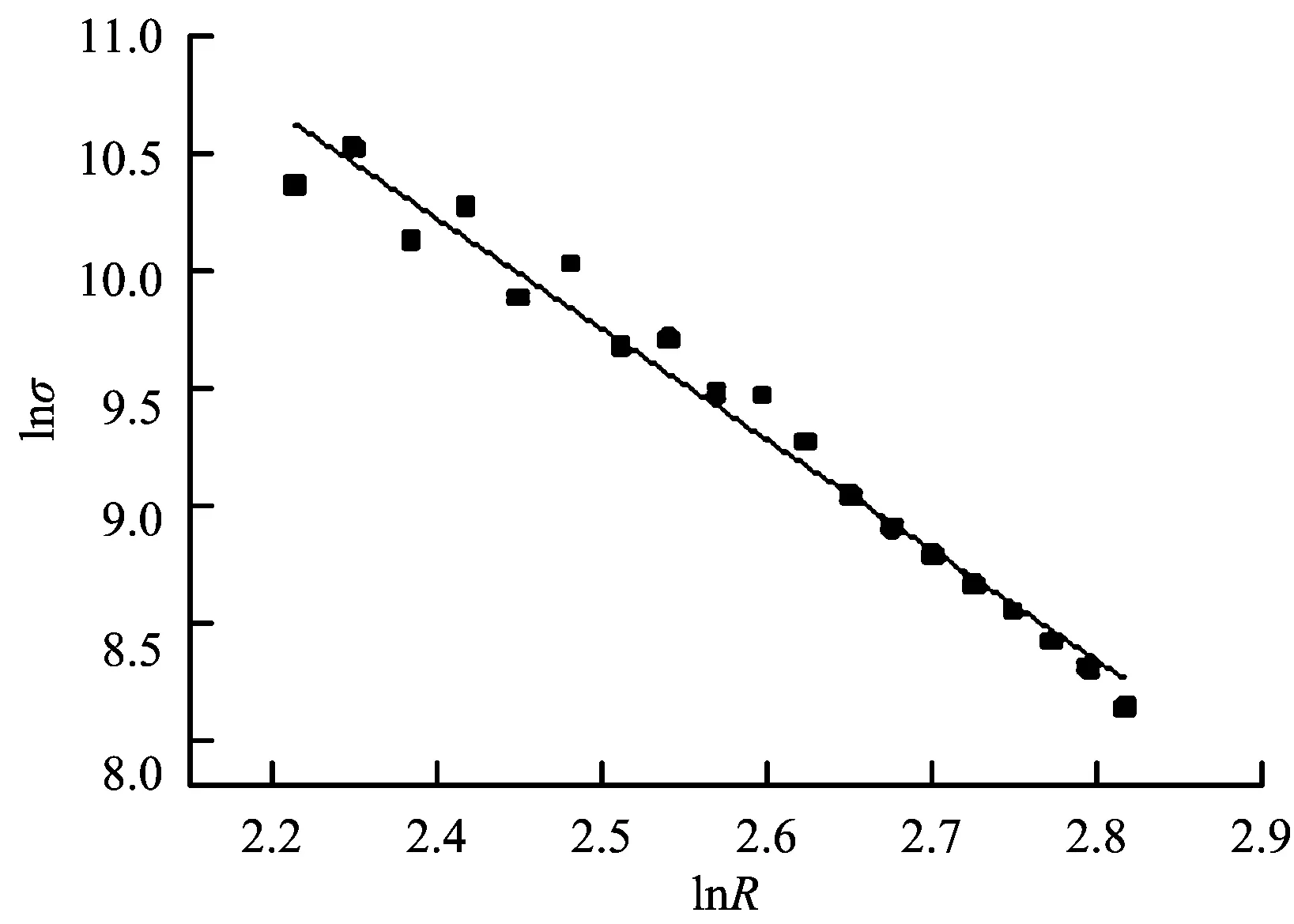
图6　lnσ-lnR拟合直线Fig.1　lnσ-lnR fitting line

截距/(lnk+α/3lnQ)斜率/(-α)截距值标准误差斜率值标准误差校正决定系数R228．182590．66064-4．695190．184070．97304

为了验证lnσ和lnR之间的线性相关关系，需要进一步对其进行回归方程的显著性检验，检验结果如表6所示。该检验结果是在显著性水平α=0.05下进行的，从表6中可知，F值为650.642 78，检验P值为5.44e-15，远小于显著性水平α。上述表明，在显著性水平α=0.05时，拟合所得的回归方程具有高度显著性，即lnσ与lnR之间具有显著线性相关关系。

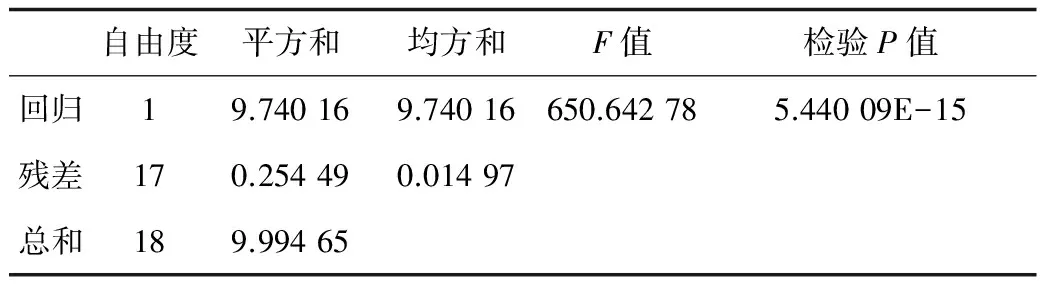
表6　应力波衰减规律拟合参数方差

综合表5数据，并结合数值模拟计算中设置的炮孔装药量Q=205.08 kg，可以推算得到k=4.18×109。最终可得，反映数值模拟计算原型的青海威斯特露天矿台阶爆破应力波的具体衰减规律为：

(17)

4　结论

1)运用量纲分析方法推导得出爆炸应力波在爆炸中远区的一般衰减规律模型，该模型与一般的模型相比较，其主要特点在于指出影响应力波强度的2个主要因素，即炸药性能参数(药量、密度和单位炸药释放能量)和距离参数。此外，在工程实践中，炸药性能等参数可提前预知，此时模型仅剩一个未知的控制参数，即距离参数，便于衰减模型的回归分析。

2)通过提取数值模拟结果中爆炸中远区范围内单元距爆源距离与其对应的应力峰值2组数据，并对二者的对数进行线性拟合，拟合结果与理论推导出的应力波衰减模型基本吻合，进一步验证了推导模型的准确性。同时，给出了反映青海威斯特德尔尼铜矿地质条件的爆炸应力波在中远区岩石中的衰减规律。

[1]胡英国,卢文波，等.岩石爆破损伤模型的比选与改进[J].岩土力学,2012(11):3278-3284.

HU Yingguo, LU Wenbo, et al. Comparison and improvement of blasting damage models for rock[J]. Rock and Soil Mechanics,2012(11):3278-3284.

[2]褚怀保,杨小林，等.煤体中爆炸应力波传播与衰减规律模拟实验研究 [J].爆炸与冲击,2012,32(2)：185-189.

CHU Huaibao, YANG Xiaolin, et al. A simulation-based experimental study on explosive stress wave propagation and attenuation in coal [J]. Explosion and Shock Waves Mar, 2012, 32(2):185-189.

[3]曹攀,颜事龙，等.基于UDEC岩体爆炸应力波衰减规律的研究 [J].爆破,2014,31(1):42-46.

CAO Pan, YAN Shilong, et al. Research on attenuation law of explosion stress wave in rock by UDEFC model [J], Blasting Mar， 2014,31(1):42-46.

[4]Hakalehto K O. The behavior of rock under impulse lodes-a study using Hopkinson Split Bar method [D]. Acta Polytechnica Scandinavica, Chemistry including Metallurgy Series, No. 81 (Helsinki, 1969).

[5]John S Rinehart. Stress Transients in Solid. Hyper Dynamics [M]. San Fe, New Mexico. 1975.

[6]戴俊.岩石动力学特性与爆破理论(第2版)[M]. 北京：冶金工业出版社,2013:146-148.

[7]李彰明,冯强.岩质边坡中应力波衰减规律探讨 [J]. 岩石力学与工程学报,1996,15(S)460-463.

LI Zhangming, FENG Qiang. Study on attenuation law of stress wave for rock slope [J]. Chinese Journal of Rock Mechanics and Engineering, 1996,15(S):460-463.

[8]史晓鹏,张银平,袁本胜.爆炸荷载作用下应力波衰减规律研究 [J]. 矿冶,2010,19(3)：15-17.

SHI Xiaopeng, ZHANG Yinping, YUAN Bensheng. Research on weaken rules of stress wave by explosion loads [J]. Set， 2010, 19(3):15-17.

[9]WEI Sun, SHI Yan, JIANG Shaofei. Research on the attenuation law of stress wave propagation in concrete media [J]. Advanced Materials Research, 2013,671(674):758-767.

[10]王明洋, 钱七虎. 爆炸应力波通过节理裂隙带的衰减规律[J]. 岩土工程学报, 1995,17(2):42-46.

WANG Mingyang, QIAN Qihu. The attenuation law of blast stress wave through joint fissure zone[J]. Journal of Rock Mass Engineering, 1995,17(2):42-46.

[11] 孙冰,袁登,等.爆炸应力波在层状节理岩体中的传播规律试验研究[J].中国安全生产科学技术, 2015, 11(11):118-123.

SUN Bing, YUAN Deng, et al. Experimental study on propagation law of explosion stress wave in bedding joint rock mass[J]. Journal of Safety Science and Technology, 2015, 11(11):118-123.

[12]XU Guangming, WU Hongwei. Dimensional analysis and centrifuge modeling of quay wall of large-diameter bottomless cylinders [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10):1544-1552.

[13]HU Hao, LIU Feng. Density-functional-theory formulation of classical and quantum Hooke’s law[J]. Science China, 2014,57(4):692-698.

[14]杨锋平,孙秦.屈服准则及切线模量修正的弹塑性计算模型[J].力学学报,2010,42(4)：804-810.

YANG Fengping, SUN Qin. A new computational model of metal plasticity based on Von Misses criterion correction and tangent modulus [J]. Chinese Journal of Theoretical and Applied Mechanics, 2010,42(4):804-810.

[15]SHEN Lijun, PAN Lizhou, HE Fubao. Study on the generalized Prandtl-Reuss constitutive equation and the corotational rates of stress tensor [J]. Applied Mathematics and Mechanics, 1998,19(8):735-743.