数塔中的方程问题

2017-04-13河南省商丘市谢集一中476032魏祥勤

数理化解题研究 2017年2期

关键词：列数奇数正整数

河南省商丘市谢集一中(476032) 魏祥勤 ●

数塔中的方程问题

河南省商丘市谢集一中(476032) 魏祥勤 ●

下面结合一道“数塔”问题，构造一元二次方程探究第几行的数字是一个已知数，对此问题进行分析、探究并进行一些拓展，供参考．

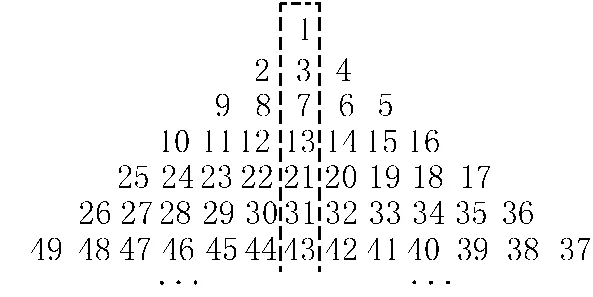
例1 把数字按照如图所示排列起来，从上开始，依次为第一行、第二行、第三行、…，中间用虚线围成一列，从上到下依次为1、5、13、 25、…，则在中间这列数中，第___行的数是761，写出推理过程．

解观察数字组成的塔形排列，易于发现仅仅在奇数行，中间是一个数字，位于矩形围出的范围内，数字1、5、13、25、…都是奇数，如果每个数字都减去1，得出数字是:0，4，12，24，…，分别除以2得出数字0，2，6，12，…，则变为:0，1×2，2×3，3×4，…，因此下一个数字应当1+2 ×4×5=41，验证如下:左起29到36，右起37到45，猜想成立，因此奇数行第n行中间数字是2n(n－1)+1，令2n (n－1)+1=761，即是n2－n－380=0，解得:n=20或者是n=－19(应舍去)，只取n=20，即是在中间这列数中，第20行的数字是761．

例2 观察下列数塔，写出第n行中间的数字规律．确定第几行中间的数字是1261?

解观察数字1、3、7、13、21、31、43、…，上面数字都减去1，得出数字0，2，6，12，20，30，42，…分别是数字0× 1、1×2、2×3、3×4、4×5、5×6、6×7，…，因此第n行中间数字是1+n(n－1)．

令1+n(n－1)= 1261，即是n2－n－1260 =0，解得:n=36或者是n=－35(应舍去)，只取n=36，即是在中间这列数中，第36行的数字是1261．

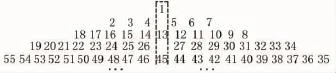
例3 观察下列数塔，写出第n行中间的数字规律．确定第几行中间的数字是211?

解观察数字1、4、11、22、37、…，上面数字都减去1，得出数字0、3、10、21、36、…，分别可以写成0，1×3，2×5，3×7，4× 9，…，可以发现第n行中间的数字规律是1+(n－1)×〔2(n－1)+1〕．令1+(n－1)×〔2(n－1)+1〕=211即是2(n－1)2+(n－1)－210=0，解得n=11或者是n=－9．5(应舍去)，只取n=11，即是在中间这列数中，第11行的数字是211．

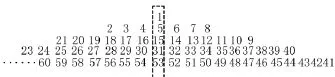
例4 观察下列数塔，写出第n行中间的数字规律．确定第几行中间的数字是1221．

解观察数字1、5、15、31、53、…，上面数字都减去1，得出数字0、4、14、30、52、…，分别可以写成0，1×4，2×7，3×10，4×13，…，可以发现第n行中间的数字规律是1+ (n－1)×〔3(n－1)+1〕．令1+(n－1)×〔3(n－1) +1〕=1221即是3(n－1)2+(n－1)－1220=0，解得n =21或者是n=－58/3(应舍去)，只取n=21，即是在中间这列数中，第21行的数字是1221．一般规律:从1开始的连续正整数构成的“数塔”，中间数字具有下面的规律:①如果第一行是数字1，从第二行开始，下面一行比上面相连一行多2k个数字(k是正整数)，则第n行中间数字是1+(n－1)〔k(n－1)+1〕;判断第几行中间的数字是形如uv2+v+1的数字(u、v都是正整数)，只需解关于n的一元二次方程k(n－1)2+(n－1)－(uv2+v)=0，得出正整数解即可(如果没有正整数解，则此种情况不存在)．特别地，当u=k时，方程k(n－1)2+(n－1)－(kv2+v)=0的正整数解是 n=v+1．另一个解是 n=－(为负数，需舍去);只取n=v+1．②如果第一行是数字1，从第二行开始，下面一行比上面相连一行多(2k－1)个数字(k是正整数)，则第n行中间数字是1+2(n－1)〔(2k－1)(n－1)+1〕;判断第几行中间的数字是形如1+2v(vu+1)的数字(u、v都是正整数)，只需解关于n的一元二次方程(2k－1)(n－1)2+(n－1)－(uv2+ v)=0，得出正整数解即可(如果没有正整数解，则此种情况不存在)．特别地，当u=2k－1时，方程(2k－1)(n－1)2+(n－1)－［(2k－1)v2+v)］=0的正整数解是n=v +1．另一个解是，即n=－(为负数，需舍去)．只取n=v+1．