基于离散曲波变换字典和二维局部离散余弦变换字典组合的面波压制

毕云云,汪金菊,徐小红,屈光中,张 洋

(1.合肥工业大学计算机与信息学院,安徽合肥 230009;2.合肥工业大学数学学院,安徽合肥 230009)



基于离散曲波变换字典和二维局部离散余弦变换字典组合的面波压制

毕云云1,汪金菊2,徐小红1,屈光中1,张 洋1

(1.合肥工业大学计算机与信息学院,安徽合肥 230009;2.合肥工业大学数学学院,安徽合肥 230009)

根据地震记录中面波和反射波形态结构的差异性,将基于离散曲波变换字典和二维局部离散余弦变换字典(2D-LDCT)组合的形态成分分析法应用于地震数据的面波压制。首先选取离散曲波变换字典来稀疏表示面波分量,选取二维局部离散余弦变换字典来稀疏表示反射波分量,然后建立地震记录在两种字典下的面波分离模型,最后通过块协调松弛算法求解该模型来分离出两种分量,实现对面波的有效压制。合成地震记录及实际地震记录试验处理结果表明,该方法在有效压制强面波干扰的同时,能够较好地保护反射波信号。

稀疏表示;面波压制;形态成分分析;离散曲波变换;二维局部离散余弦变换

面波是反射波地震勘探中常见的噪声干扰,在炮点附近呈扇形分布,视速度低、能量强,且具有频散的特点,严重影响了中深层的有效反射,降低了地震资料的信噪比。因此,有效的面波压制对后续地震资料的处理和解释具有重要作用。目前有多种面波压制方法,如一维频率域滤波法、f-k滤波法、Hilbert-Huang变换法、小波变换法、曲波变换法等。

一维频率域滤波法将每一道地震记录进行傅里叶变换后通过设计合适的高通滤波器来滤除面波成分[1],但高通滤波同时会丢失低频部分的反射波信号,产生吉布斯现象;f-k滤波法考虑了面波频率低、视速度低的特点[2],但当面波能量远强于反射波时,会造成有效波严重失真,并在滤波器的边界产生新的相干噪声;孔庆丰[3]利用Hilbert-Huang变换较高的时频分辨率来压制面波,但对于有效波与面波重叠较多的区域不能很好地识别区分;张华等[4]、岳龙等[5]通过小波变换的多尺度特性识别出面波区域,减小了去除面波时对有效信号的影响,但小波变换只对处理点奇异有效,对于地震记录的曲线奇异特征不能有效地表示;曲波变换对线和超平面的奇异性表示优于小波变换[6],ZHENG等[7]、董烈乾等[8]对曲波域中主要含面波的尺度和方向的系数进行阈值处理,也能够有效去除面波干扰。

实际地震数据通常由多种信号成分组成,只采用单一变换不能有效地表现数据的内部结构特征。近年来稀疏表示理论迅速发展,并被不断引入到地震数据处理领域[9-11]。STARCK等[12-13]提出了以信号的稀疏性和形态多样性为基础的形态成分分析(Morphological Component Analysis,MCA)方法,WANG等[14]将其引入地震记录面波压制处理,提出了基于单道处理的压制面波的改进MCA法。陈文超等[15]和李海山等[16]根据反射波与面波形态结构的差异,将一维局部离散余弦变换与一维小波变换分别作为反射波和面波的稀疏表示字典,通过求解稀疏优化问题实现了两者的分离。以上方法都是以单道记录为处理对象,没有充分考虑到道与道之间的相关性,增加了数据的计算复杂度。XU等[17]对整个二维地震记录进行处理,联合二维非抽样离散小波变换(2D-Undecimated Discrete Wavelet Transform,2D-UDWT)和二维局部离散余弦变换(2D-Local Discrete Cosine Transform,2D-LDCT)构成超完备字典,将其应用到MCA方法分离反射波和面波分量的问题中,也得到了较好的压制效果。

鉴于小波变换自身的局限性,本文在XU等[17]研究工作的基础上,将表示性能更好的离散曲波变换作为面波的稀疏表示字典,将2D-LDCT作为反射波的稀疏表示字典,并对2D-LDCT字典的内部结构进行优化,更好地分离出了面波分量和反射波分量,实现了对面波的有效压制。最后用理论模型数据和实际地震资料进行了应用测试。

1 MCA方法简介

1.1 信号的稀疏表示问题

稀疏表示能够在变换域内用尽可能少的原子的线性组合来逼近原信号,对于信号x=[x1,x2,…,xN]T,若只有m个元素为非0值,绝大部分元素为零,则称该信号是稀疏的,其稀疏度为m[18]。如果信号在时域不满足稀疏性特征,可以通过适当的变换使其稀疏化。一般地,一个信号x可由K个原子dk的线性叠加表示:

(1)

其中,字典D是N×K矩阵,若D的列数大于行数,即K>N,称此字典为超完备字典;αk(k=1,2,…,K)为x在字典D=[d1,d2,…,dK]下的稀疏表示系数,α的稀疏度可由α的0范数‖α‖0表示,即α中非0分量的个数。若α是稀疏的,则信号x可在字典D下得到稀疏表示,即该信号可表示为一小部分原子的线性叠加。

1.2 形态成分分析(MCA)原理

MCA方法将多种具有不同原子特征的字典联合起来构成超完备冗余字典,从而获得更加稀疏的信号表示方式,实现对不同形态信号分量的有效分离[12-13]。假定输入的待处理信号s∈RN×1由N个形态特征不同的分量sn线性组成,即:

(2)

式中:sn(n=1,2,…,N)表示不同形态成分的信号分量;超完备字典Tn(n=1,2,…,N)为sn对应的稀疏表示字典;αn(n=1,2,…,N)为sn在相应字典下的稀疏表示系数,同时MCA理论假定对于混合信号中的每一种信号分量sn,其在相应的字典Tn下都能得到非常稀疏的表示,而在字典Tk≠n下不能得到有效的稀疏表示。混合信号s的稀疏表示可以描述为求解下列问题:

(3)

按照基追踪(Basis Pursuit,BP)算法和匹配追踪(Matching Pursuit,MP)算法[19]的思想,对(3)式中的约束条件适当松弛,可转化为求解如下问题:

(4)

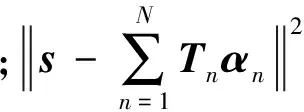
1.3MCA方法面波分离模型

假设含面波地震记录的每道信号是有效反射波和面波的线性叠加,则单炮地震记录可表示为:

(5)

式中:sr,sg,n分别表示有效反射波分量、面波分量和随机噪声。在该模型中加入随机噪声分量为0均值的高斯白噪声,可以提高模型的普适性。

对于反射波分量sr,用超完备字典Tr∈MN×Lr进行稀疏表示时,有:

(6)

得到的表示系数αr非常稀疏,字典Tr能够有效地稀疏表示反射波分量sr。

对于面波分量sg,用超完备字典Tg∈MN×Lg进行稀疏表示时,有:

(7)

得到的表示系数αg也非常稀疏,则字典Tg能够有效地稀疏表示面波分量sg，如果字典Tr不能很好地稀疏表示面波分量,字典Tg不能很好地稀疏表示反射波分量，则单炮地震记录s可利用由Tr和Tg联合组成的超完备字典进行稀疏表示,并通过求解如下的最优化问题实现面波与反射波的分离:

(8)

2 面波压制方法原理

MCA算法的关键环节是字典组合的选择。根据MCA理论,2种字典不仅需要能够分别稀疏地表示各信号分量,它们的原子波形也需要具有明显的差异性。由于反射波和面波的形态结构差别很大,因此只要为这2种信号分量找到相应的稀疏表示字典,就能够在相应的稀疏域中对其进行有效地稀疏表示。

2.1 离散曲波变换字典表示面波分量

地震记录中的面波分量频率低、视速度低,具有频散特性,且面波与反射波同相轴斜率差异较大,而离散曲波变换具有非常好的局部性、各向异性和很强的方向性,能够有效地表示波前和具有线状特征的同相轴[21],因而我们选择离散曲波变换作为面波的稀疏表示字典。

(9)

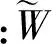
(10)

(11)

本文采用基于快速wrapping算法的离散曲波变换作为面波的稀疏表示字典,对于反射波频带和面波频带交叠的区域,离散曲波变换能够充分利用良好的方向识别能力,有效地分离出面波分量。

2.2 2D-LDCT字典表示反射波分量

地震记录反射波分量局部相关性强,具有明显的波动特征,而局部离散余弦变换(LDCT)是类似于傅里叶变换的一种实值变换,它对具有高度相关性的信号有非常好的能量聚集性,能够有效地捕捉信号的局部结构特征,准确地描述不同时段的信号特性,自适应地跟踪信号的变化[23-24],因而我们选择2D-LDCT作为反射波分量的稀疏表示字典。

LDCT是一种基于重叠正交基或双正交基的变换,本文采用的是Ⅳ型局部余弦基,其定义如下:

(12)

其中,hi=ai+1-ai表示信号的第i段,gi(t)是定义在区间Ii=[ai-ηi,ai+1+ηi+1]上相互重叠的光滑窗函数,它将信号分成分段信号,且满足ai+ηi≤ai+1-ηi+1,ηi和ηi+1分别为左右两侧的重叠半径。LDCT一般通过先对信号做折叠分段处理,再对其进行快速Ⅳ型LDCT得到。原始的2D-LDCT字典只能处理方阵数据,本文对其进行了优化,无需在数据变换时将其扩充为方阵,使其能自适应地处理任意大小的地震数据,从而实现对反射波有效的描述和稀疏表示。

2.3 稀疏表示性能对比

我们利用两组实验来对比说明不同字典对反射波和面波信号的稀疏表示性能。实验选取经过滤波后不含面波的实际地震记录作为实验反射波信号,该记录共240道,每道采样点数为1024,如图1所示。选取受到强面波干扰的实际地震记录切片作为实验面波信号,该记录共64道,每道采样点数为1024,如图2所示。选取的2D-LDCT字典为离散Ⅳ型余弦变换,窗口宽度为10;选取的离散曲波变换字典为基于wrapping算法的快速离散曲波变换。为了更好说明离散曲波变换字典和2D-LDCT字典对两种信号分量稀疏表示的优越性,并与2D-UDWT字典稀疏表示的性能进行对比,其小波母函数采用消失矩为10的Symmlet小波。对2组实验信号分别用这3种字典进行稀疏表示,将得到的系数根据幅值进行排序,并按相同的比例系数将其中较小幅值的系数置0,再分别通过3种变换的逆变换求出各自的重构信号,计算重构信号与原始信号的重构相对误差,以此来评价各字典对反射波和面波的稀疏表示能力,重构误差越小,则稀疏表示能力越强。

图1 实验反射波信号

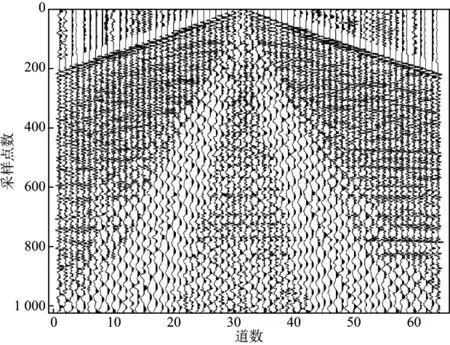
图2 实验面波信号

反射波信号在各变换字典下的重构误差随置0比例系数的变化曲线如图3所示,可以看出,在置0比例系数相同的情况下,2D-LDCT字典重构误差较小,即能用更少的系数稀疏表示反射波分量,2D-UDWT字典的稀疏表示能力适中,而离散曲波变换字典重构误差最大,即不能很好的稀疏表示反射波分量;面波信号在各变换字典下的重构误差随置0比例系数的变化曲线如图4所示,可以看出,在置0比例系数相同的情况下,离散曲波变换字典重构误差较小,即能用更少的系数稀疏表示面波分量,而2D-LDCT字典的重构误差最大,即不能很好的稀疏表示面波分量,2D-UDWT字典的重构误差介于两者之间。离散曲波变换字典和2D-LDCT字典体现出的对2种信号成分稀疏表示能力的差异,使得基于这2种字典组合的MCA方法可用于地震记录中面波信号和反射波信号的分离。

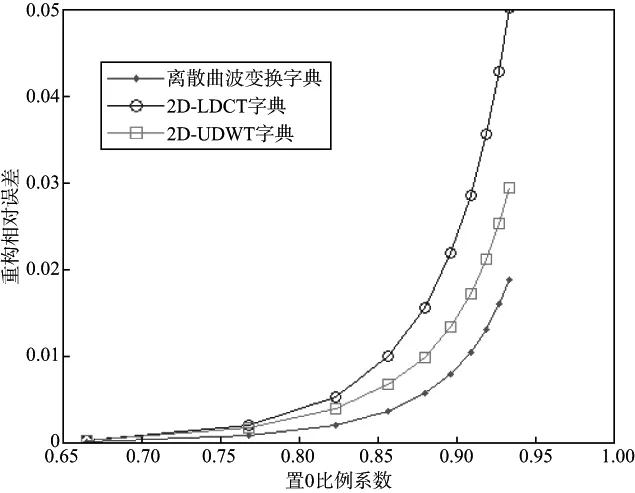
图4 含强能量面波地震信号在3种不同字典下稀疏性比较

2.4 面波分离模型的求解方法

在实际处理中,求解(8)式中的最优化问题得到的系数维度较高,需占用大量内存,因此,将(8)式进一步转化:

Trrr=0Tgrg=0

(13)

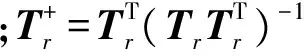
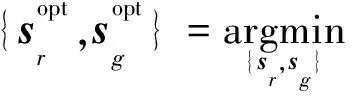
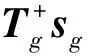
(14)

上述问题的求解以BCR算法为基础,分别固定一种信号成分不变,更新另一种信号分量,通过迭代阈值法最小化该分量的惩罚项和约束项得到更新系数,再与其相应的表示字典相乘即可得到更新后的信号成分。在对面波成分进行更新时做相应的修改,利用离散曲波变换字典对其进行5层分解后,保留曲波域中主要含面波的尺度和方向上的系数不变(主要分布在Fine尺度和Detail尺度的低频高波数方向),对其它系数进行阈值处理,使得反射波分量与面波分量的分离效果更加明显。

3 合成数据实验

图5a为利用雷克子波合成的有效反射波记录,该记录共240道,每道采样点数为1000,道间距为30m,包含3个反射同相轴,主频为40Hz,最大振幅为3,信号采样间隔为5ms,记录长度为5s;图5b为加入的面波,面波利用扫描信号合成,频带范围为5～15Hz,最大振幅为12;图5c为合成的受面波干扰的地震记录,其信噪比为-22.46dB,在面波与反射波重叠的区域,反射波几乎被全部掩盖,受损严重。应用本文方法对图5c含面波合成地震记录进行处理,设置迭代次数为50,分离出的反射波分量和面波分量如图6a和图6b所示。为了进一步说明本文方法的有效性,分别采用基于2D-UDWT与2D-LDCT字典组合的MCA法和曲波变换法对该地震记录进行面波压制处理。其中,2D-UDWT字典和2D-LDCT字典分别稀疏表示面波分量和反射波分量,曲波变换使用快速离散wrapping算法。图6c和图6d为基于2D-UDWT与2D-LDCT字典组合的MCA法得到的反射波分量和面波分量,图6e和图6f分别为曲波变换法处理后得到的反射波分量和面波分量。为了更清晰地显示3种方法的压制效果,分别选取合成反射波记录和各方法处理后得到的反射波记录的第100道数据进行波形和振幅谱分析,得到的结果如图7所示。

由图6a和图6b可以看出,合成地震数据中的面波和反射波得到了有效的分离,反射波分量中只有极少部分的面波残留;分离出的面波分量中也几乎不含反射波,图7c中分离出的反射波第100道记录的波形和合成的反射波单道记录的波形非常接近。由图6c 和图6d的分离结果可以看出,该方法能较好地去除面波分量,但同时也损失了少量反射波信息,图7e 中反射波单道记录的波形中还存在部分干扰。由图6e 和图6f中的处理结果可以看出,该方法能较好地去除面波分量,同时能很好地保留反射波分量的信息,面波分量中几乎不含反射波,但图7g中反射波单道记录的波形中还含有较多干扰。由图7中各种方法分离出的反射波单道记录的振幅谱可以看出,相比于本文方法,基于2D-UDWT与2D-LDCT字典组合的MCA法和曲波变换法都损失了部分低频成分的有效信号。以上各种方法的面波压制效果可以用处理后的信噪比和均方根误差(RMSE)来客观评价,得到的结果如表1所示。从表1中可以看出,采用本文基于离散曲波变换和2D-LDCT字典组合的MCA方法压制面波后,地震数据的信噪比提高最多,均方根误差最小,这表明本文方法能够对地震记录中的面波进行更有效地去除。

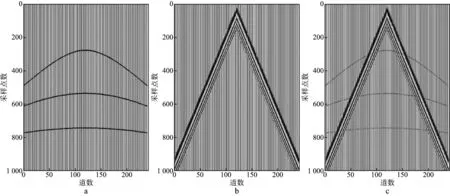
图5 合成地震记录a 合成反射波记录; b 合成面波记录; c 受面波干扰的合成地震记录

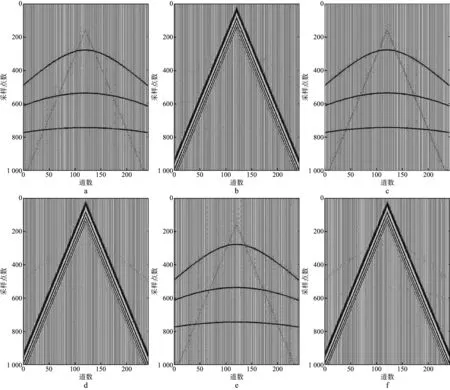
图6 合成地震记录面波压制效果对比a 本文方法得到的反射波; b 本文方法得到的面波; c 基于2D-UDWT与2D-LDCT字典组合的MCA法得到的反射波; d 基于2D-UDWT与2D-LDCT字典组合的MCA法得到的面波; e 曲波变换法得到的反射波; f 曲波变换法得到的面波

表1 不同方法压制面波效果对比

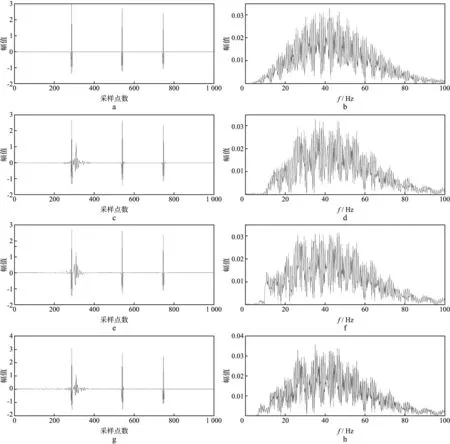
图7 合成地震记录单道波形及振幅谱a 图5a第100道记录的波形; b 图7a的振幅谱; c 图6a第100道记录的波形; d 图7c的振幅谱; e 图6c第100道记录的波形; f 图7e的振幅谱; g 图6e第100道记录的波形; h 图7g的振幅谱

4 实际数据应用

为验证本文方法对实际地震记录处理的有效性,将此方法用于压制图8所示的地震记录中的面波,该地震记录共240道,每道采样点数为1024,采样间隔为4ms。图9a和图9b展示了其第115道记录的波形和振幅谱,分析可知,面波主要分布在低频部分0～20Hz范围内。设置迭代次数为30次,LDCT窗口宽度为16,分离后的反射波和面波如图10a和图10b所示。为了进一步说明本文方法的有效性,分别应用基于2D-UDWT与2D-LDCT字典组合的MCA法和曲波变换法对该地震记录进行处理。其中,2D-UDWT字典和2D-LDCT字典分别稀疏表示面波分量和反射波分量,曲波变换使用快速离散wrapping算法。图10c和图10d为基于2D-UDWT与2D-LDCT字典组合的MCA法处理后得到的反射波分量和面波分量,图10e和图10f为曲波变换法处理后得到的反射波分量和面波分量。为了更清晰地显示3种方法的压制效果,分别选取利用各方法处理后得到的反射波记录的第115道记录进行波形和振幅谱分析,如图11所示。

图8 含面波干扰的实际地震记录

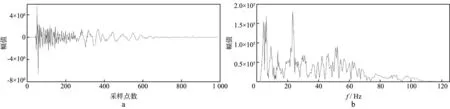
图9 实际地震记录第115道记录的波形(a)及其振幅谱(b)

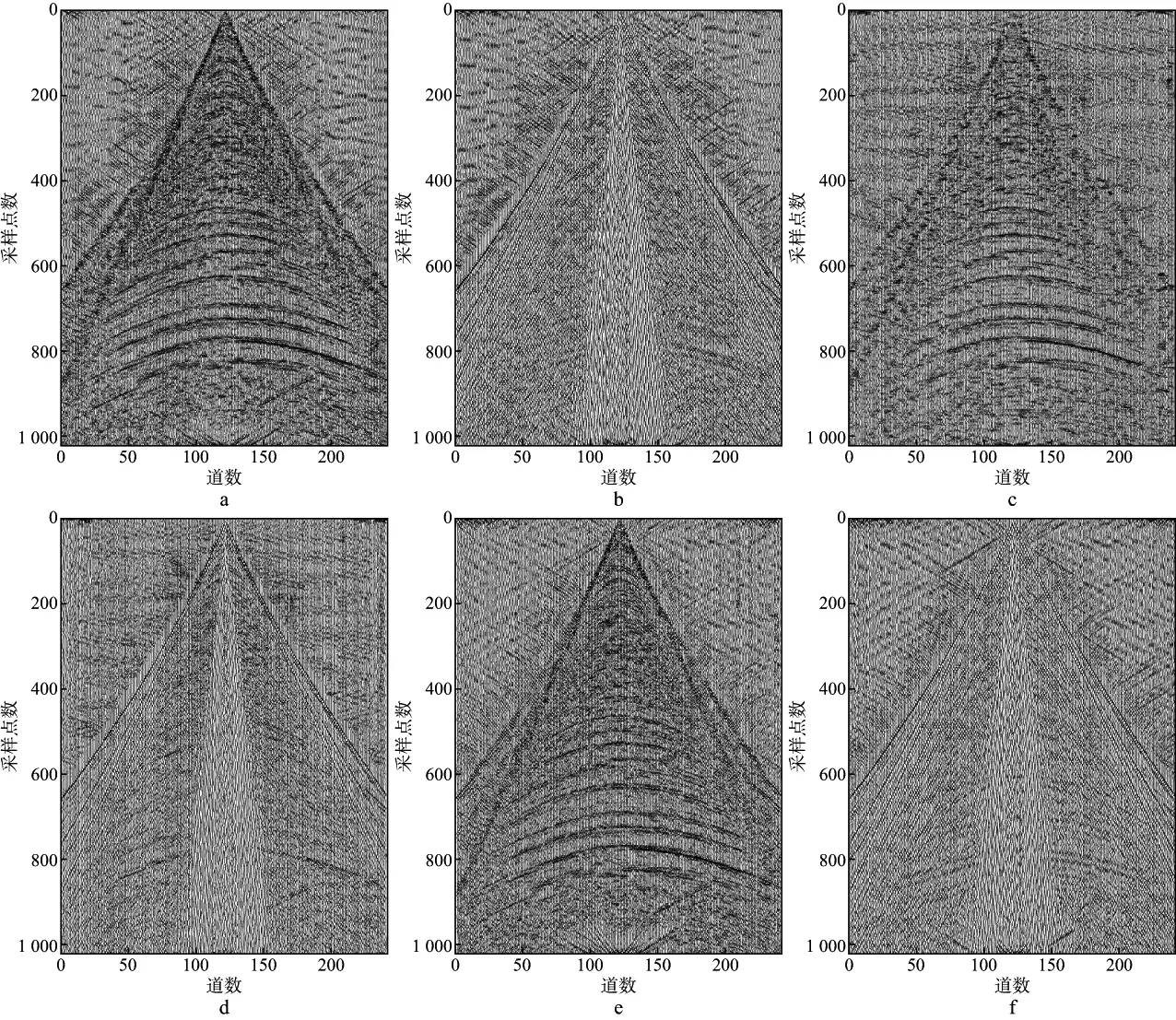
图10 实际地震记录面波压制效果对比a 本文方法得到的反射波; b 本文方法得到的面波; c 基于2D-UDWT与2D-LDCT字典组合的MCA法得到的反射波; d 基于2D-UDWT与2D-LDCT字典组合的MCA法得到的面波; e 曲波变换法得到的反射波; f 曲波变换法得到的面波

从图10中可以看出,应用本文方法分离出来的反射波分量同相轴较为清晰,并且较好地保留了原地震记录的有效信息,分离出的面波只含有微弱的反射波;利用基于2D-UDWT与2D-LDCT字典组合的MCA法和曲波变换法得到的反射波中都几乎不含面波信号,但分离出来的面波中都含有少量明显的反射波信号。从图11中单道记录的波形及振幅谱可以看出,相比于本文方法得到的结果,基于2D-UDWT与2D-LDCT字典组合的MCA法和曲波变换法得到的反射波单道记录的波形都存在不同程度的幅度失真,并且两种方法得到的反射波都损失了部分低频成分的信息。这表明,本文方法压制面波的效果较好,能够很好地将反射波和面波分量分离,同时对有效信号的损害较小。

图11 实际单道地震记录的波形及振幅谱对比a 图10a第115道记录的波形; b 图11a的振幅谱; c 图10c第115道记录的波形; d 图11c的振幅谱; e 图10e第115道记录的波形; f 图11e的振幅谱

5 结束语

本文利用MCA方法压制地震数据中的面波,根据面波和有效反射波的形态结构差异,分别选取表示性能更好的离散曲波变换和优化后的2D-LDCT字典作为两种信号分量的稀疏表示字典,建立地震记录在两种字典下的面波分离模型,在采用块协调松弛算法来求解该模型时,将曲波域内主要含面波的尺度和方向上的系数保持不变,对其他系数进行阈值处理,获得了明显的压制效果。和基于2D-UDWT与2D-LDCT字典组合的MCA法、曲波变换法相比,本文方法在有效压制面波干扰的同时能很好地保护反射波信号的波形特征,是一种更精确有效的面波压制方法。然而实际地震数据中往往含有多种干扰,使用变换字典组合的方法进行面波压制,会存在将原有其它干扰转变为新的干扰噪声的问题,如何有效规避此问题还需要进一步研究。

[1] 张军华,吕宁,田连玉,等.地震资料去噪方法技术综合评述[J].地球物理学进展,2006,21(2):546-553 ZHANG J H,LV N,TIAN L Y,et al.An overview of the methods and techniques for seismic data noise attenuation[J].Progress in Geophysics,2006,21(2):546-553

[2] ADIZUA O F,EBENIRO J O,EHIRIM C N.Comparative study of radial trace transform and the frequency-wave number techniques for suppressing dispersive ground roll energy from onshore seismic data(amplitude spectrum approach)[J].International Journal of Research and Innovations in Earth Science,2016,3(1):11-14

[3] 孔庆丰.基于Hilbert-Huang变换的面波压制方法研究[J].石油物探,2012,51(5):446-450 KONG Q F.Surface wave suppressing method based on Hilbert-Huang transform[J].Geophysical Prospecting for Petroleum,2012,51(5):446-450

[4] 张华,潘冬明,张兴岩.二维小波变换在去除面波干扰中的应用[J].石油物探,2007,46(2):147-150 ZHANG H,PAN D M,ZHANG X Y.Application of 2-D wavelet transformation in eliminating surface wave interference[J].Geophysical Prospecting for Petroleum,2007,46(2):147-150

[5] 岳龙,刘怀山,尹燕欣,等.基于连续小波变换的面波衰减方法研究[J].石油物探,2016,55(2):214-222 YUE L,LIU H S,YIN Y X,et al.Attenuation of ground roll based on continuous wavelet transform[J].Geophysical Prospecting for Petroleum,2016,55(2):214-222

[6] CANDES E J,DONOHO D L.New tight frames of Curvelets and optimal representations of objects with piecewise C2singularities[J].Communications on Pure and Applied Mathematics,2004,57(2):219-266

[7] ZHENG J J,YIN X Y,ZHANG G Z,et al.The surface wave suppression using the second generation curvelet transform[J].Applied Geophysics,2010,7(4):325-335

[8] 董烈乾,李振春,王德营,等.第二代Curvelet变换压制面波方法[J].石油地球物理勘探,2011,46(6):897-904 DONG L Q,LI Z C,WANG D Y,et al.The ground roll suppression method using the second generation of Curvelet transform[J].Oil Geophysical Prospecting,2011,46(6):897-904

[9] MA J,PLONKA G,CHAURIS H.A new sparse representation of seismic data using adaptive easy-path wavelet transform[J].Geoscience and Remote Sensing Letters,2010,7(3):540-544

[10] LEONARDO T D,DANIEL D,RENATO R.L.Seismic signal processing:some recent advances[J].IEEE International Conference on Acoustic,Speech and Signal Processing (ICASSP),2014:2362-2366

[11] 周亚同,刘志峰,张志伟.形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J].石油物探,2015,54(5):560-568 ZHOU Y T,LIU Z F,ZHANG Z W.Seismic signal reconstruction under the morphological component analysis framework combined with DCT and curvelet dictionary[J].Geophysical Prospecting for Petroleum,2015,54(5):560-568

[12] STARCK J L,ELAD M,DONOHO D L.Redundant multiscale transforms and their application for morphological component separation[J].Advance in Imaging and Electron Physics,2004,132(82):278-348

[13] STARCK J L,ELAD M,DONOHO D L.Image decomposition via the combination of sparse representation and a variational approach[J].IEEE Transactions on Image Processing,2005,14(10):1570-1582

[14] WANG W,CHEN W C,LEI J L,et al.Ground-roll separation by sparsity and morphological diversity and promotion[J].Expanded Abstracts of 80thAnnual Internet SEG Mtg,2010:3705-3710

[15] 陈文超,王伟,高静怀,等.基于地震信号波形形态差异的面波噪声稀疏优化分离方法[J].地球物理学报,2013,56(8):2771-2782 CHEN W C,WANG W,GAO J H,et al.Sparsity optimized separation of ground roll noise based on morphological diversity of seismic waveform components[J].Chinese Journal of Geophysics,2013,56(8):2771-2782

[16] 李海山,吴国忱,印兴耀.基于形态分量分析的保幅面波压制方法[J].石油地球物理勘探,2013,48(3):351-358 LI H S,WU G C,YIN X Y.Amplitude-preserved surfacewave attenuation method based on morphological component analysis[J].Oil Geophysical Prospecting,2013,48(3):351-358

[17] XU X H,QU G Z,ZHANG Y,et al.Ground roll separation of seismic data based on morphological component analysis in two-dimensional domain[J].Applied Geophysics,2016,13(1):116-126

[18] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306

[19] DONOHO D L,ELAD M.Optimally sparse representation in general (nonorthogonal) dictionaries vial1minimization[J].Proceedings of the National Academy of Sciences of the United States of America,2003,100(5):2197-2202

[20] ELAD M,STARCK J L,QUERRE P,et al.Simultaneous cartoon and texture image inpainting using morphological component analysis[J].Applied and Computational Harmonic Analysis,2005,19(3):340-358

[21] HERRMANN F J,DELI W,GILLES H,et al.Curvelet-based seismic data processing:a multiscale and nonlinear approach[J].Geophysics,2008,73(1):A1-A5

[22] STARCK J L,CANDES E J,DONOHO D L.The curvelet transform for image denoising[J].IEEE Transactions on Image Processing,2002,11(6):670-684

[23] APARNA P,DAVID S.Adaptive local cosine transform for seismic image compression[J].2006 International Conference on Advanced Computing and Communications,2006:254-257

[24] MALLAT S G.A wavelet tour of signal processing:the sparse way[M].3rded.San Diego,California:Academic Press,2008:401-426

[25] SARDY S,BRUCE A G,TSENG P.Block coordinate relaxation methods for nonparametric wavelet denoising[J].Journal of Computational and Graphical Statistics,2000,9(2):361-379

(编辑：朱文杰)

Ground roll attenuation based on the combination of discrete curvelettransform dictionary and two-dimensional local discrete cosinetransform dictionary

BI Yunyun1,WANG Jinju2,XU Xiaohong1,QU Guangzhong1,ZHANG Yang1

(1.SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei230009,China;2.SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China)

According to the different morphological characteristics between ground roll and reflected wave in seismic record,we use morphological component analysis based on the combination of discrete curvelet transform dictionary and two-dimensional local discrete cosine transform dictionary to attenuate ground roll.Firstly,we choose discrete curvelet transform dictionary to sparsely represent ground roll,and two-dimensional local discrete cosine transform dictionary to sparsely represent reflected wave respectively.Then the ground roll separation model of seismic record can be constructed under the two dictionaries.Finally,by solving the model using block coordinate relaxation algorithm,we can separate the ground roll and reflected wave and thus attenuate ground roll effectively.The processing results of synthetic and real seismic records indicate that our method can not only suppress strong ground roll noise but also preserve reflected wave effectively.

sparse representation,ground roll attenuation,morphological component analysis,discrete curvelet transform,two-dimensional local discrete cosine transform

2016-06-20;改回日期：2016-08-13。

毕云云(1991—),女,硕士在读,主要从事信号与信息处理方面的研究。

汪金菊(1978—),女,副教授，主要从事信号与信息处理方面的研究。

国家重大科研装备研制项目“深部资源探测核心装备研发”(ZDYZ2012-1-06-05)资助。

P631

A

1000-1441(2017)02-0222-10

10.3969/j.issn.1000-1441.2017.02.009

This research is financially supported by the National Scientific Equipment Development Project of China (Grant No.ZDYZ2012-1-06-05).