基于Hampel三截尾函数的储层弹性和物性参数同步反演

李志勇,张家树,蔡涵鹏,胡光岷

(1.电子科技大学通信与信息工程学院,四川成都611731;2.西南交通大学信号与信息处理四川省重点实验室,四川成都610031)



基于Hampel三截尾函数的储层弹性和物性参数同步反演

李志勇1,张家树2,蔡涵鹏1,胡光岷1

(1.电子科技大学通信与信息工程学院,四川成都611731;2.西南交通大学信号与信息处理四川省重点实验室,四川成都610031)

常规的地震反演方法通常假设噪声信号服从高斯分布，以此构建出的目标函数在特定地区反演效果好，但其普适性较小。假设地震噪声信号和岩石物理模型误差服从高斯分布且带有加性脉冲噪声，引入Hampel三截尾函数构造能够同时压制高斯噪声和脉冲噪声的反演目标函数，利用牛顿法求解目标函数得到储层弹性和物性参数反演的迭代公式，并通过阈值的选择适应噪声分布不同的地区。该算法利用Hampel三截尾函数构建加权矩阵,能在一定程度上自适应调节地震数据、岩石物理约束和先验信息之间的权重，消除地震和岩石物理噪声的统计性误差造成的反演不稳定性，最终得到稳定的储层弹性和物性参数反演结果。通过理论模型测试和实际资料应用显示了算法的稳定性和可靠性。

AVO反演;岩石物理反演;联合反演;高斯噪声;脉冲噪声;Hampel三截尾函数

20世纪80年代,勘探工作者发现地震数据的反射振幅随炮检距的变化可以用于油气检测,从而发展了利用纵波AVO属性进行构造解释和岩性识别的AVO分析技术[1]。在AVO分析技术的基础上发展起来的AVO反演方法,可从地震叠前资料中获得反映地下储层信息的纵、横波速度和密度等信息,为储层预测与烃类检测提供量化依据。随着AVO反演方法逐渐趋于成熟,人们开始利用地震、测井和岩心等数据的互补特性,从井间地震数据中反演地层岩石的弹性参数和物性参数[2-3]。与单纯的AVO反演相比,这种多源信息联合反演的方法不仅可以减少反演多解性的问题,还能够同时获得多种储层参数，因此受到了学术界和工业界的广泛关注。

多源信息联合反演研究多于一个的目标函数在给定区域上的最优化,求取目标函数最小或最大值所对应的一组模型参数,并把这组模型参数看成是满足这些条件的“最佳解”。显然,目标函数不同,最佳解也就不一样。为了求解方便,绝大多数方法都假设噪声信号服从高斯分布[4-7],利用统计性方法和确定性方法求解目标函数。前者将观测数据和模型参数都视为随机变量,用统计的方法来确定解所服从的概率分布,得到的是满足观测数据的解具有多大概率;而后者认为观测数据和模型参数都是确定量,因而用数理方程或代数方法求解反演问题,根据观测数据求得模型参数。BOSCH等[8]在贝叶斯框架下将地震似然函数、岩石物理似然函数和先验信息结合,构建服从高斯分布的后验概率密度函数,利用统计性方法(蒙特卡罗采样)获得储层的孔隙度和波阻抗。统计性方法存在不完全依赖于初始猜测、反演过程理论上不会陷入局部极值的优点。但其缺点也十分明显,就是计算工作量大、效率低,难以完全满足大规模地球物理反演的要求。BOSCH等[9-10]在贝叶斯框架下利用确定性方法(最小二乘法)对信噪比相对较高的地震叠后资料进行了孔隙度和波阻抗同步反演。李志勇等[11]在BOSCH等研究成果的基础上尝试利用AVO正演模拟和Gasmann方程建立储层物性参数与地震叠前观测数据之间的联系,利用最小二乘法同步反演获得纵横波速度、密度、孔隙度、含水饱和度和泥质含量。研究发现,利用最小二乘准则可以方便地计算最速下降方向和修正步长,并且具有不错的收敛速度。但对于信噪比相对较低的叠前地震数据,使用最小二乘准则会使误差数据得到相同的权重,严重影响反演结果的稳定性。另外,由于速度模型与埋藏深度通常存在正比关系,而储层物性参数服从0～1的截断分布,因此，建立储层物性参数与弹性参数之间的岩石物理模型时,误差同样不完全服从高斯分布[12]。LI等[13]采用自适应加权系数来调整地震似然函数、岩石物理似然函数和先验信息之间的权重,提高了多参数同步反演方法的稳定性,但无法从根本上消除脉冲噪声信号的影响。

对于脉冲噪声信号,TAYLOR等[14]使用L1范数建立目标函数,得到了比传统的L2范数更鲁棒的解。然而,L1范数在残差接近于0的时候存在奇异点,容易导致反演算法的不稳定。在TAYLOR等研究成果的基础上,很多学者研究了基于L1范数的变形算法。如BUBE等[15]采用迭代加权算法来最小化L1/L2混合范数。GUITTON等[16]、吕晓春等[17]采用Huber范数建立目标函数,在残差较小时采用L2范数,在残差较大时采用L1范数,避免了L1范数的奇异性带来的优化困难。Huber范数在一定程度上减小了脉冲噪声对反演算法的影响,但由于阈值点为无穷大,也没有从根本上消除脉冲噪声的影响。随着脉冲噪声比例的增加,Huber范数将会失效。考虑到Biweight范数能够对大于设定阈值的噪声信号予以忽略,JI[18]将Biweight范数引入到地震反演中,提高了算法对脉冲噪声的抑制能力。刘洋等[19]提出了针对非高斯噪声的地震叠前非高斯反演概念和思想,构造了能同时压制高斯噪声和脉冲噪声的混合范数并将其作为目标函数。岳碧波等[20]假设地震噪声信号服从非高斯α稳定分布,提出了基于非高斯α稳定分布的最小Lp范数地震反演方法。另外,考虑到广义极值概率密度分布函数在一定情况下具有逼近任意概率密度分布函数的能力,ZHANG等[21]提出了基于广义极值分布的AVO反演方法。

误差协方差矩阵是L2范数的一个重要统计性质,其正确估计是进行数据完美匹配的前提。由于协方差矩阵对脉冲噪声的存在非常敏感,因此脉冲噪声可能导致对协方差矩阵估计的错误,解决这一问题最直接的办法就是采用鲁棒性估计方法修正协方差矩阵。本文假设地震噪声信号和岩石物理模型误差服从高斯分布且带有加性脉冲噪声,引入Hampel三截尾函数构建重加权算子来对协方差矩阵进行修正。Hampel三截尾函数结合了Huber范数和Biweight范数的优点,不仅能够减小脉冲噪声对协方差矩阵估计的影响,而且还能将超过阈值的噪声信号完全排除,提高算法对高斯噪声和脉冲噪声的抑制能力。

1 技术方法

1.1 岩石物理模型

地震资料能够提供纵、横波速度和密度等信息,利用这些信息可以进一步估算孔隙度、饱和度和泥质含量等储层物性参数。地震勘探中通常使用Gassmann方程来定量描述低频条件下储层物性参数发生变化时介质有效弹性模量的相应变化。采用基于Gassmann方程的流体替换技术可以得到不同孔隙流体条件下砂岩储层的体积模量和剪切模量[22]:

(1)

(2)

式中:Ksat和μsat分别是流体饱和岩石的有效体积模量和有效剪切模量;Kdry和μdry分别是干岩石的有效体积模量和有效剪切模量,可以采用改进的Hashin-Strikman弹性模量上边界计算得到[23];K0是岩石基质的有效体积模量;Kfl是孔隙流体的有效体积模量;φ是孔隙度。

对于任意岩石,给定各成分体积含量之后,其等效模量将处于上、下界限之间,但其精确的数值将依赖于几何细节。由于Gassmann-Biot理论假设岩石具有一个均匀的矿物模量,因此混合矿物常常用一种“平均矿物”来描述。本文采用最简单、但不一定是最好的界限。以砂、泥岩为例,如果岩石的矿物成分已知,那么利用Voigt-Reuss-Hill平均可以计算岩石基质的等效体积模量K0[24]:

(3)

式中:C是泥质含量,Ks和Kc分别是砂岩和泥岩的体积模量。

同理,当岩石孔隙所含流体为多相流体时,如果流体的成分已知,那么利用Reuss模型[25]可以计算孔隙流体的等效体积模量Kfl:

(4)

式中:Sw是含水饱和度;Khc是油或气的体积模量;Kbrine是地层水的体积模量。

建立岩石物理模型的另一个参数是饱和岩石的密度ρsat,该参数由岩石骨架密度ρ0和充填流体的密度ρfl按体积比例加权平均得到:

(5)

式中:ρsat,ρ0,ρfl分别为流体饱和岩石、岩石骨架和充填流体的密度。

在计算得到流体饱和岩石的体积模量Ksat,剪切模量μsat和密度ρsat之后,流体饱和岩石的纵波、横波速度公式可以表示为:

(6)

(7)

1.2 反演目标函数

文献[11]通过假设地震噪声信号和岩石物理模型误差服从高斯分布,给出了基于最小二乘法的储层弹性和物性参数同步反演目标函数:

(8)

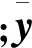
通过研究(x,y)为何值时使S(x,y)达到最小可以得到最佳解。然而,公式(8)中的协方差矩阵Cd和Cx|y对脉冲噪声十分敏感,容易导致反演算法的不稳定。本文假设地震噪声信号和岩石物理模型误差服从高斯分布且带有加性脉冲噪声,利用Hampel三截尾函数构建重加权算子对协方差矩阵进行修正。新的反演目标函数表示为:

(9)

式中:ωd和ωx|y是基于Hampel三截尾函数的重加权算子[26],可表示为:

(10)

(11)

(12)

式中:ω(e)=φ(e)/e,φ(e)=∂ρ(e)/∂e,ρ(e)是Hampel三截尾函数;ε,Δ1和Δ2是Hampel三截尾函数的阈值,用来控制函数对脉冲噪声的抑制能力,阈值越小,其抗脉冲噪声的能力越强。图1为Hampel函数和加权算子示意图。可以看出:当|ei|<ε时,Hampel函数为二次函数;当ε≤|ei|<Δ2时,Hampel函数为一次函数;当误差|ei|>Δ2时,Hampel函数为常数。由此可见,Hampel函数结合了Huber函数和Biweight函数的优点:当误差较小时,使用L2范数求解;当存在少数脉冲噪声时,使用L1范数求解;当存在大量脉冲噪声时,直接对噪声信号进行截断,从根本上排除了脉冲噪声对反演的影响。

显然,阈值的合理设置是压制高斯和脉冲噪声信号的关键。在噪声信号服从高斯分布的假设下,如果噪声信号大于某一给定阈值T,则其概率可表示为:

(13)

式中,σ表示高斯噪声信号的标准差。相应地,p{|e|>ε},p{|e|>Δ1}和p{|e|>Δ2}分别表示|e|大于ε,Δ1和Δ2的概率。ZOU等[27]提出根据数据的95.0%,97.5%和99.0%置信区间来设置ε,Δ1和Δ2,计算获得相应的阈值:

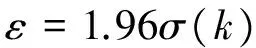
(14)

(15)

(16)

式中:σ(k)是迭代残差的瞬时标准差。一种常用的方法是利用递归公式对瞬时标准差估计进行滤波:

(17)

由于σ(k)容易受到脉冲噪声的影响,这里采用一种鲁棒性的估计方法:

(18)

式中:mad{·}表示平均绝对中值偏差,用来抑制脉冲噪声对方差估计的影响。

图1 Hampel函数(a)和由Hampel函数构建的加权函数(b)

1.3 牛顿法迭代递推公式

将公式(9)的梯度用泰勒公式展开,可以近似地得到:

(19)

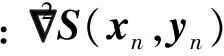
(20)

式中:

(21)

(22)

(23)

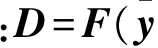
2 效果分析

2.1 模型测试一

首先由测井曲线解释得到地层岩石的孔隙度、含水饱和度和泥质含量等储层物性参数(图2a至图2c),然后根据岩石物理模型计算纵、横波速度和密度等弹性参数(图2d至图2f),最后利用叠前正演模型合成地震角道集(图3),测试其含脉冲噪声时本文方法的反演效果。地震子波采用30Hz的零相位雷克子波,道集的最小炮检距为150m,最大炮检距为4000m,炮检距间隔为350m。在反演过程中,初始模型和先验模型可以通过测井曲线滤波得到,物性参数的初始模型和先验模型相同。

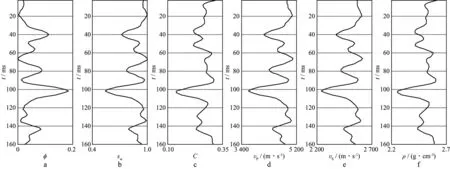
图2 利用测井曲线解释得到的储层参数(一)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

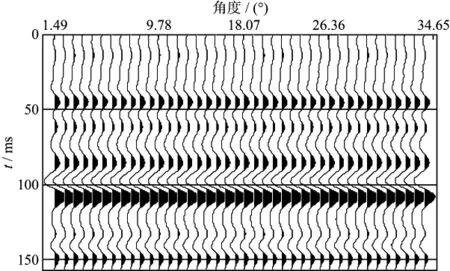
图3 利用测井数据合成的地震角道集(一)

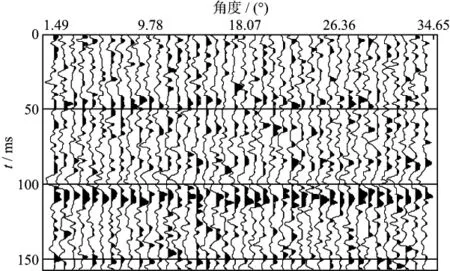
图4 加入30%脉冲噪声信号的地震角道集(一)

当地震角道集含有30%的随机脉冲噪声时(图4),分别采用最小二乘法和本文方法进行反演,结果如图5和图6所示。由图5和图6可以看出,两

者均能识别反射层位,但最小二乘法的反演结果不稳定,锯齿现象明显。这是因为使用最小二乘法会使残差得到相同的权重,脉冲噪声的存在使地震数据得到偏大的权重(Cd偏小),岩石物理约束和先验信息的权重相对减小,弹性参数和物性参数的反演结果主要来自于地震数据。本文利用Hampel三截尾函数设置加权矩阵,自适应调整Cd的大小,减小了地震脉冲噪声在目标函数中的权重,因而提高了算法对脉冲噪声的抑制能力。

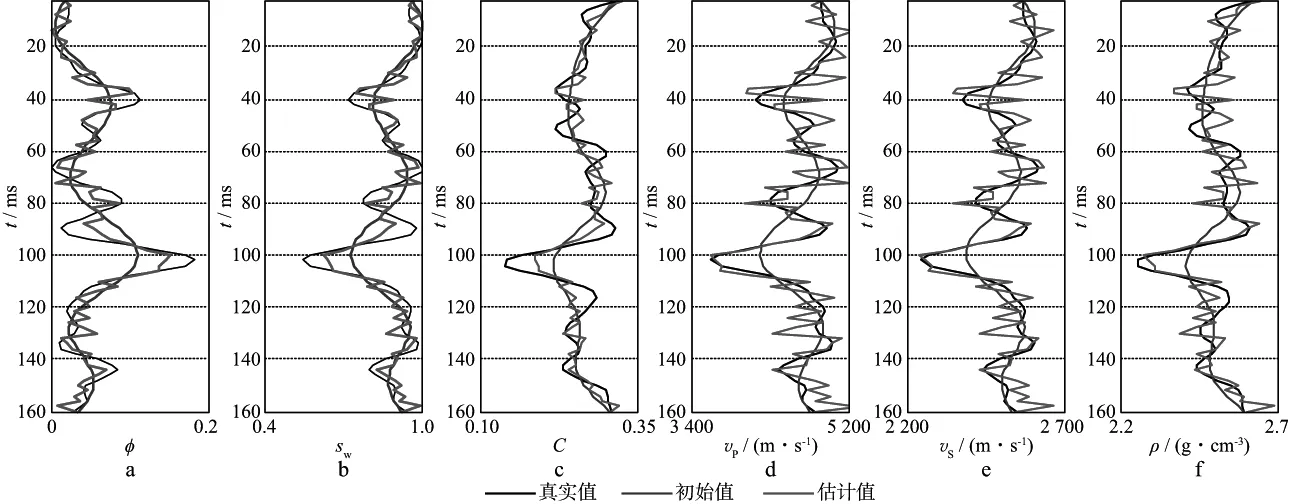
图5 利用最小二乘法反演得到的储层参数(一)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

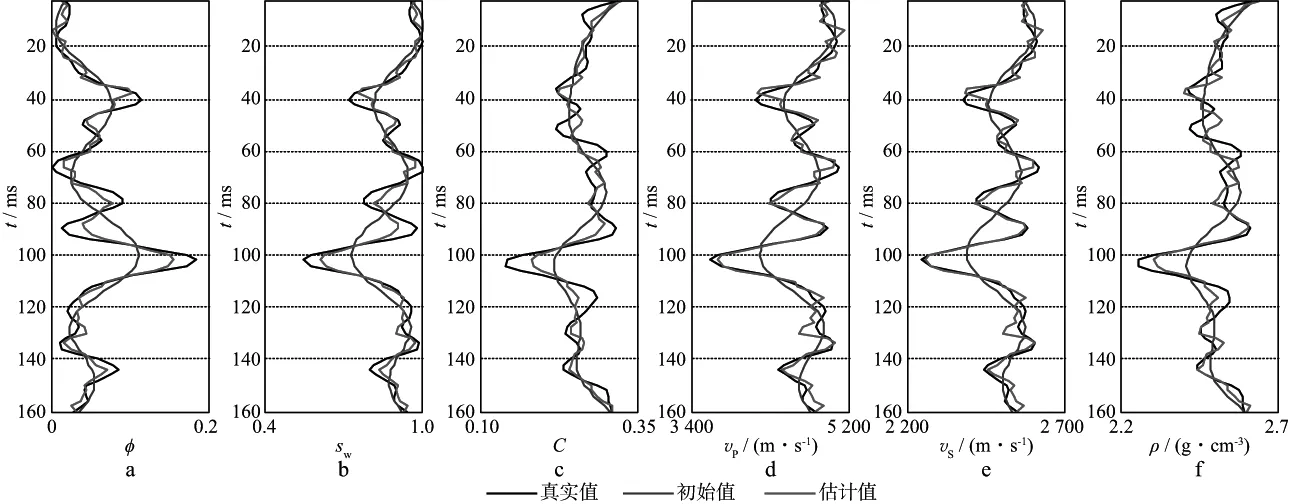
图6 利用本文方法反演得到的储层参数(一)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

2.2 模型测试二

首先由测井曲线解释得到岩石的孔隙度、含水饱和度和泥质含量等储层物性参数(图7a至图7c);然后根据岩石物理模型计算纵、横波速度和密度等弹性参数(图7d至图7f,红色曲线),并在弹性参数中加入脉冲噪声(图7d至图7f,黑色曲线);最后利用含脉冲噪声的弹性参数合成地震角道集(图8),并在地震角道集中加入30%的随机脉冲噪声(图9),分别测试岩石物理模型含脉冲噪声与岩石物理模型和地震角道集都含脉冲噪声两种情况下本文方法的反演效果。地震子波采用30Hz的零相位雷克子波,道集的最小炮检距为150m,最大炮检距为4000m,炮检距间隔为350m。在反演过程中,初始模型和先验模型可以通过测井曲线滤波得到,物性参数的初始模型和先验模型相同。

当岩石物理模型含脉冲噪声、地震角道集不含脉冲噪声时(图8),分别采用最小二乘法和本文方法进行反演,结果如图10和图11所示。由图10和图11可以看出,两者均能识别反射层位,但最小二乘法的弹性参数反演结果与真实值相差较大。这是因为脉冲噪声的存在使岩石物理模型得到偏大的权重(Cx|y偏小),地震角道集和先验信息的权重相对减小,弹性参数的反演结果主要来自于岩石物理约束。本文利用Hampel三截尾函数设置加权矩阵,自适应调整Cx|y的大小,减小了岩石物理脉冲噪声在目标函数中的权重,提高了算法对脉冲噪声的抑制能力。

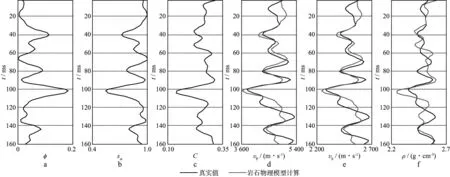
图7 利用测井曲线解释得到的储层参数(二)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

当岩石物理模型和地震角道集都含脉冲噪声时(图9),分别采用最小二乘法和本文方法进行反演,结果如图12和图13所示。由图12和图13可以看出,两者均能识别反射层位,但使用最小二乘法得到的弹性参数反演结果不稳定且偏离真实值。这是因为最小二乘法会使残差数据得到相同的权重,增加了脉冲噪声在目标函数中的权重。同时,地震数据和岩石物理约束条件以及先验信息之间的相对关系变得不稳定,反演结果既有可能来自于地震数据,也有可能来自于岩石物理约束。本文方法能够自适应调整地震数据、岩石物理约束和先验信息之间的相对关系,提高算法的稳定性,因此弹性参数和物性参数的反演结果都与真实值吻合较好。

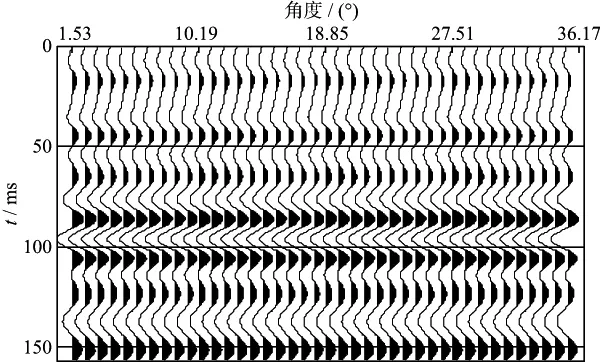
图8 利用测井数据合成的地震角道集(二)

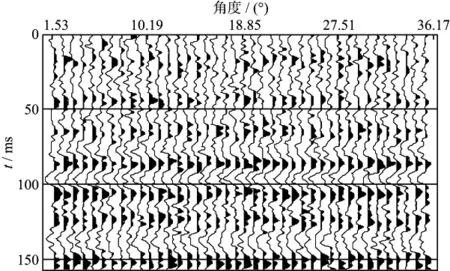
图9 加入30%随机脉冲噪声后的地震角道集(二)

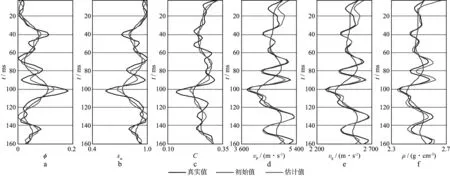
图10 利用最小二乘法反演得到的储层参数(二)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

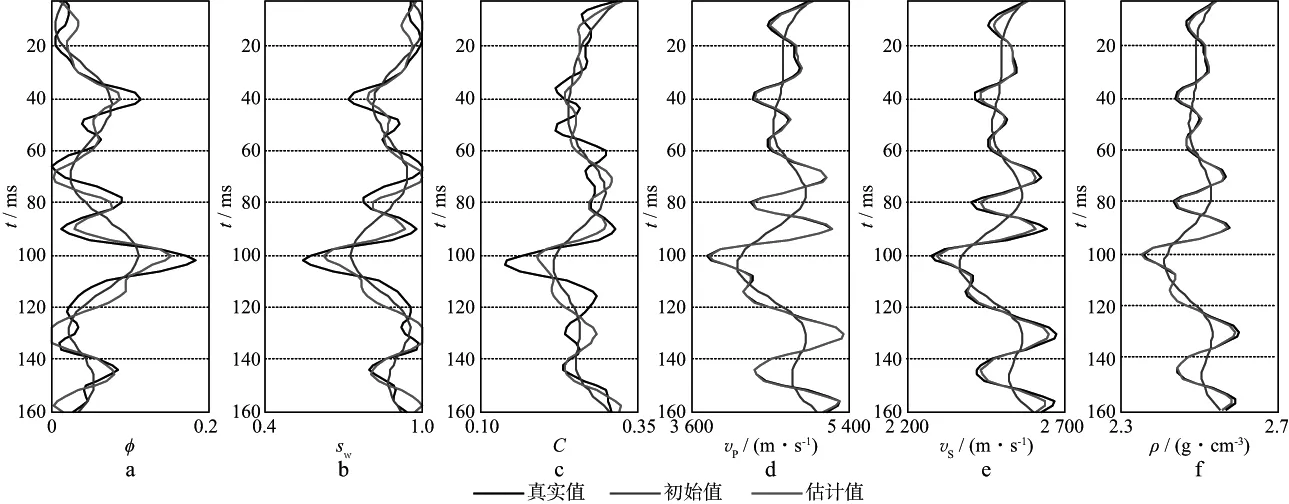
图11 利用本文方法反演得到的储层参数(二)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

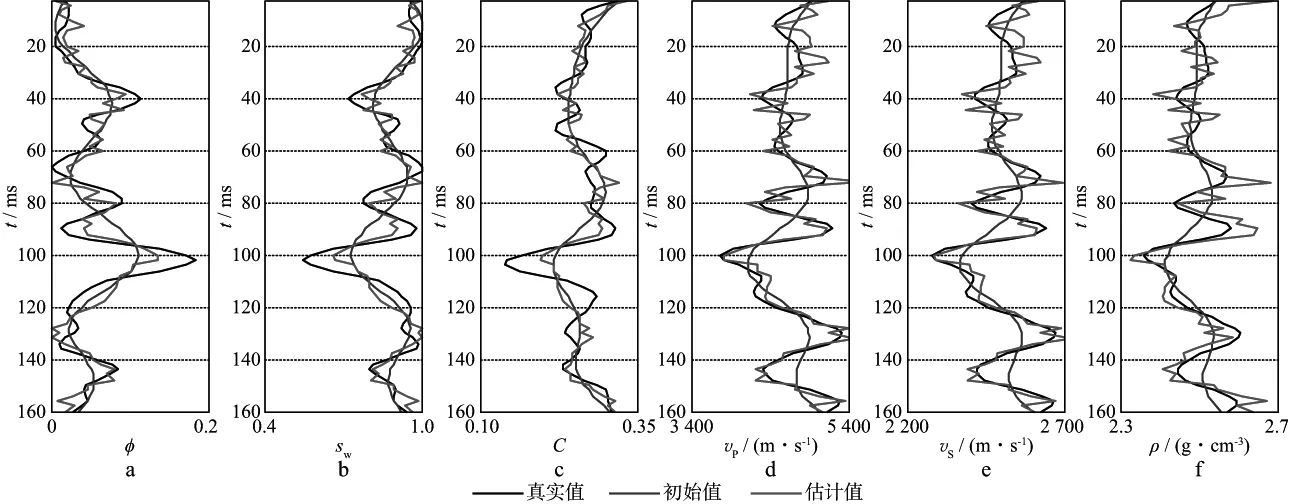
图12 利用最小二乘法反演得到的储层参数(二)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

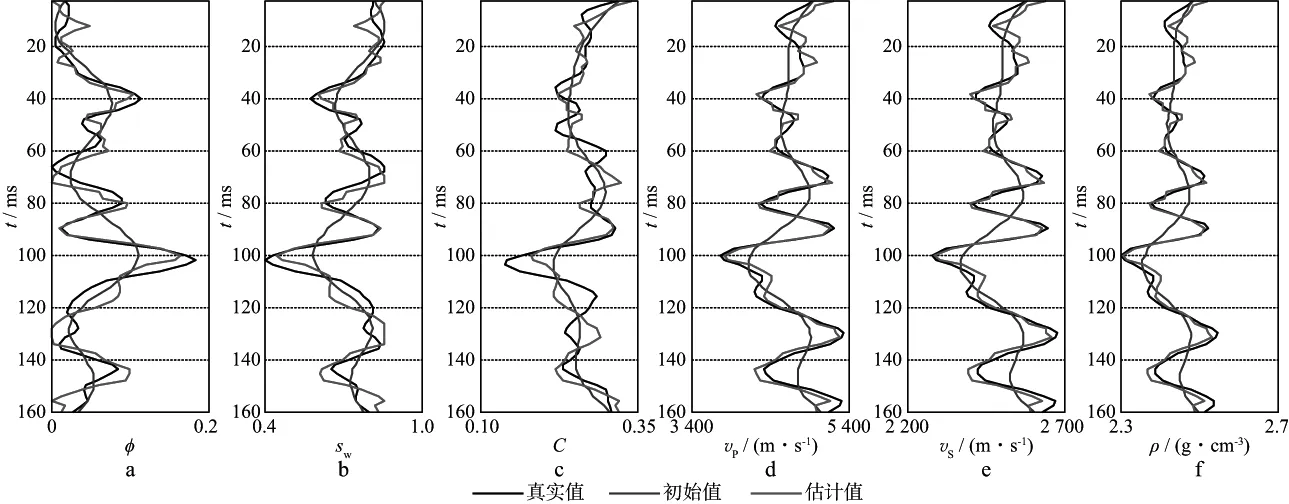
图13 利用本文方法反演得到的储层参数(二)a 孔隙度; b 含水饱和度; c 泥质含量; d 纵波速度; e 横波速度; f 密度

2.3 应用实例

利用苏里格气田实际数据对本文方法的应用效果进行了研究。研究区目的层是上古生界二叠系底部H8—S1砂层组,属沼泽背景下的辫状河沉积,天然气成藏条件复杂。同时,构造对天然气聚集不起主要控制作用,储层经过强烈的成岩作用改造,有效孔隙以次生孔隙为主,具有低孔、低渗和非均质性严重的特点。图14为苏里格气田A测线地震剖面,该测线共有601道,道间距为25m,时间采样率为2ms。该剖面经过6口井,各井所在CDP号分别为1665,1691,1792,1856,2007和2044,图中黑色曲线为H8层位。

图14 苏里格气田叠后地震剖面

图15是A测线地震角道集的方差分布图,可以看出,沿着该测线方向的方差变化较大。在这种情况下,地震数据、岩石物理约束和先验信息之间的相对权重关系十分复杂,基于噪声信号高斯分布的假设往往会导致反演结果不稳定。图16a是位于CDP1856处的实际地震角道集,可以看出,1970ms处角道集的振幅远远大于上覆地层的振幅。图16b是利用最小二乘法反演结果生成的地震角道集,图16c是实际角道集与合成角道集的残差分布图,可以看出,当上覆地层的地震残差很小时,1970ms处的地震残差仍然很大。显然,图16c中的角道集残差已经不再满足噪声信号服从高斯分布的假设,假设地震残差服从高斯分布且带有加性脉冲噪声更为合理。

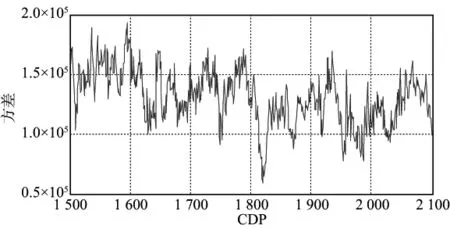
图15 地震角道集的方差分布

图17和图18分别是采用最小二乘法和本文方法进行反演得到的结果。可以看出,当岩石物理模型和地震角道集都含有脉冲噪声时,最小二乘法的反演结果并不理想。一方面,岩石物理模型的脉冲噪声使反演得到的弹性参数偏离初始模型的趋势;另一方面,地震角道集的脉冲噪声使反演得到的物性参数变得不可靠。本文方法通过设置加权矩阵自适应调整地震角道集、岩石物理约束和先验信息之间的相对权重,在一定程度上能够压制脉冲噪声的影响,提高算法的稳定性。

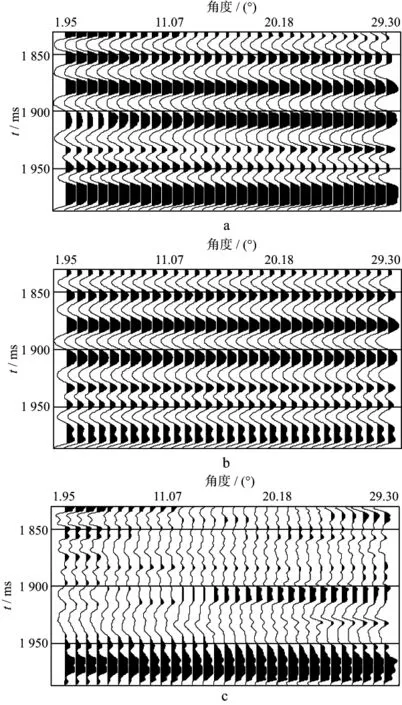
图16 CDP1856处地震角道集a 实际角道集; b 合成角道集; c 实际角道集与合成角道集的残差

沿着H8层位曲线,弹性参数与物性参数的初始模型和先验模型可以通过6口井的内插、外推模拟得到。图19是利用本文方法反演得到的纵波速度、横波速度剖面,图20是利用本文方法反演得到的密度、孔隙度、含水饱和度和泥质含量剖面。可以看出,弹性参数和物性参数的反演结果稳定性较好,且反演结果与测井曲线较为吻合。

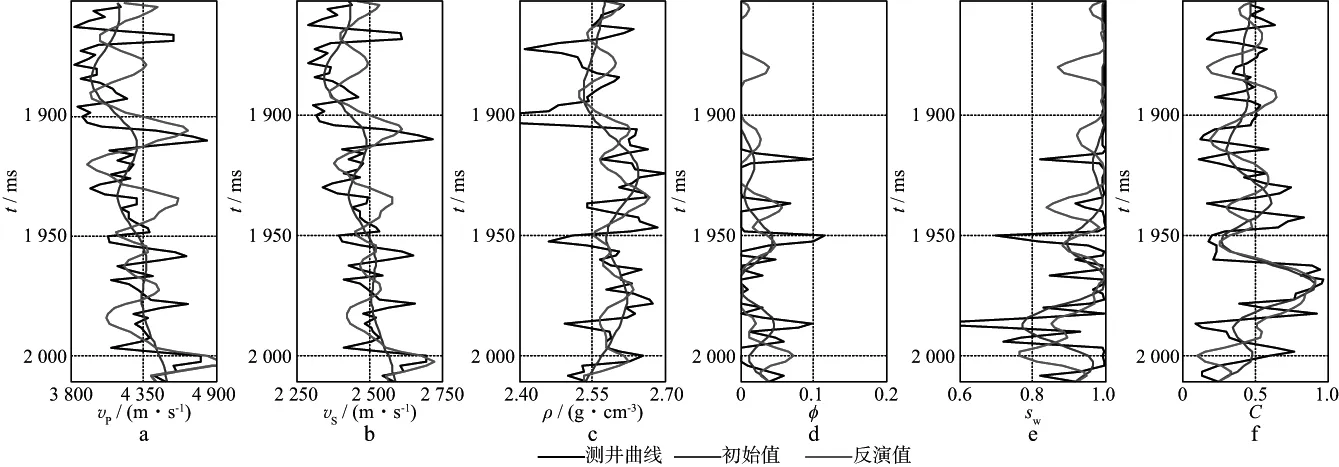
图17 CDP1856处最小二乘法反演结果a 纵波速度; b 横波速度; c 密度; d 孔隙度; e 含水饱和度; f 泥质含量

图18 CDP1856处本文方法反演结果a 纵波速度; b 横波速度; c 密度; d 孔隙度; e 含水饱和度; f 泥质含量

图19 纵波速度(a)和横波速度(b)反演结果

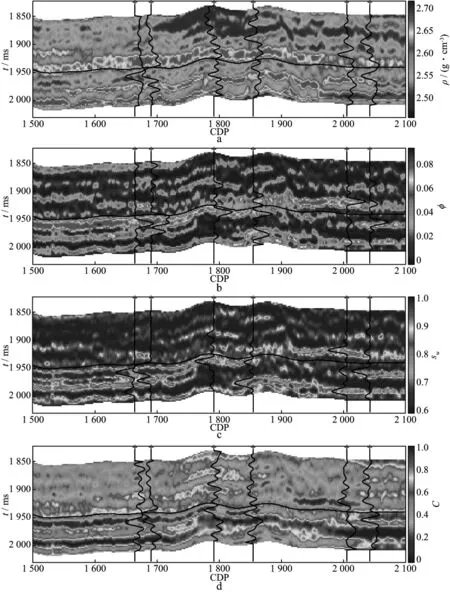
图20 密度(a)、孔隙度(b)、含水饱和度(c)和泥质含量(d)反演结果

3 结束语

储层弹性和物性参数同步反演是提取岩性参数的一条重要途径。随着勘探目标由构造油气藏转向岩性油气藏,同步反演的应用越来越广泛。本文假设地震噪声信号和岩石物理模型误差服从高斯分布且带有加性脉冲噪声,利用Hampel三截尾函数构建加权矩阵对反演目标函数进行约束,通过反演残差自适应调整目标函数中的加权矩阵,提高了同步反演算法对高斯噪声和脉冲噪声的适应能力。

当观测数据不完全服从高斯分布时,多源信息约束反演本身是严重不稳定的。利用Hampel三截尾函数构建加权矩阵能在一定程度上自适应调节各个目标函数之间的权重,消除地震和岩石物理噪声的统计性误差造成的反演不稳定性,最终得到稳定的储层弹性和物性参数反演结果。

[1] OSTRANDER W J.Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J].Geophysics,1984,49(10):1637-1648

[2] 胡华锋,印兴耀,吴国忱.基于贝叶斯分类的储层物性参数联合反演方法[J].石油物探,2012,51(3):225-232 HU H F,YIN X Y,WU G C.Joint inversion of petrophysical parameters based on Bayesian classification[J].Geophysical Prospecting for Petroleum,2012,51(3):225-232

[3] 印兴耀,孙瑞莹,张广智,等.基于分形高频初始模型和低频先验信息的物性参数随机反演[J].石油物探,2014,53(5):537-544 YIN X Y,SUN R Y,ZHANG G Z,et al.Stochastic inversion of reservoir physical property parameters based on high-frequency initial model from fractal and low-frequency prior information[J].Geophysical Prospecting for Petroleum,2014,53(5):537-544

[4] 潘昱洁,李大卫,杨锴.确定性反演和随机反演对井约束条件的需求分析[J].石油物探,2011,50(4):345-349 PAN Y J,LI D W,YANG K.A comparison between the requirements of multi-well constrained conditions in deterministic inversion and stochastic inversion[J].Geophysical Prospecting for Petroleum,2011,50(4):345-349

[5] 张繁昌,代荣获,刘汉卿,等.叠前地震道集AVA多频信息同时反演[J].石油物探,2014,53(4):453-460 ZHANG F C,DAI R H,LIU H Q,et al.Multi-frequency AVA simultaneous inversion for pre-stack seismic gathers[J].Geophysical Prospecting for Petroleum,2014,53(4):453-460

[6] 桂金咏,高建虎,雍学善,等.致密储层敏感弹性参数叠前同步反演方法[J].石油物探,2015,54(5):541-550 GUI J Y,GAO J H,YONG X S,et al.A prestack simultaneous inversion method for sensitive elastic parameters of tight reservoir[J].Geophysical Prospecting for Petroleum,2015,54(5):541-550

[7] 王官超,杜启振.基于包络目标函数的弹性波波形反演[J].石油物探,2016,55(1):133-141 WANG G C,DU Q Z.Elastic full waveform inversion based on envelop objective function[J].Geophysical Prospecting for Petroleum,2016,55(1):133-141

[8] BOSCH M,CARA L,RODRIGUES J,et al.A Monte Carlo approach to the joint estimation of reservoir and elastic parameters from seismic amplitudes[J].Geophysics,2007,72(6):O29-O39

[9] BOSCH M.The optimization approach to lithological tomography:combining seismic data and petrophysics for porosity predictio[J].Geophysics,2004,69(5):1272-1282

[10] BOSCH M,CARVAJAL C,RODRIGUES J,et al.Petrophysical seismic inversion conditioned to well-log data:methods and application to a gas reservoir[J].Geophysics,2009,74(2):O1-O15

[11] 李志勇,钱峰,胡光岷,等.储层弹性与物性参数地震叠前同步反演的确定性优化方法[J].地球物理学报,2015,58(5):1706-1716 LI Z Y,QIAN F,HU G M,et al.Prestack seismic joint inversion of reservoir elastic and petrophysical parameters using deterministic optimization method[J].Chinese Journal of Geophysics,2015,58(5):1706-1716

[12] LI Z,LIU Z,SONG C,et al.Generalized Gaussian distribution based adaptive mixed-norm inversion for non-Gaussian noise[J].Expanded Abstracts of 85thAnnual Internat SEG Mtg,2015:3926-3930

[13] LI Z Y,SONG B B,ZHANG J S,et al.Joint elastic and petrophysical inversion using prestack seismic and well log data[J].Exploration Geophysics,2015,47(4):331-340

[14] TAYLOR H L,BANKS S C,MCCOY J F.Deconvolution with the1 norm[J].Geophysics,1979,44(1):39-52

[15] BUBE K P,LANGAN R T.Hybrid1/2 minimization with applications to tomography[J].Geophysics,1997,62(4):1183-1195

[16] GUITTON A,SYMES W.Robust inversion of seismic data using the Huber norm[J].Geophysics,2003,68(4):1310-1319

[17] 吕晓春,顾汉明,成景旺.基于 Huber函数的频率域全波形反演[J].石油物探,2013,52(5):544-552 LV X C,GU H M,CHEN J W.Huber norm based full waveform inversion in frequency domain[J].Geophysical Prospecting for Petroleum,2013,52(5):544-552

[18] JI J.Robust inversion using biweight norm and its application to seismic inversion[J].Exploration Geophysics,2012,43(2):70-76

[19] 刘洋,张家树,胡光岷,等.叠前三参数非高斯反演方法研究[J].地球物理学报,2012,55(1):269-276 LIU Y,ZHANG J S,HU G M,et al.A study of the three-term non-Gaussian pre-stack inversion method[J].Chinese Journal of Geophysics,2012,55(1):55-64

[20] 岳碧波,彭真明,张启衡.基于α稳定分布的地震反演方法[J].地球物理学报,2012,55(4):1307-1317 YUE B B,PENG Z M,ZHANG Q H.Seismic inversion method based onαdistribution[J].Chinese Journal of Geophysics,2012,55(4):1307-1317

[21] ZHANG J,LV S,LIU Y,et al.AVO inversion based on generalized extreme value distribution with adaptive parameter estimation[J].Journal of Applied Geophysics,2013,98(1):11-20

[22] MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook:tools for seismic analysis of porous media[M].Cambridge:Cambridge University Press,2009:168-169

[23] GRANA D,DELLA R E.Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion[J].Geophysics,2010,75(3):O21-O37

[24] Hill R.The elastic behaviour of a crystalline aggregate[J].Proceedings of the Physical Society(Section A),1952,65(5):349-354

[25] REUSS A.Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle[J].Journal of Applied Mathematics and Mechanics,1929,9(1):49-58

[26] HAMPEL F R,RONCHETTI E M,ROUSSEEUW P J,et al.Robust statistics:the approach based on influence functions[M].New York:Wiley,1986:379-380

[27] ZOU Y,CHAN S C,NG T S.A robust m-estimate adaptive filter for impulse noise suppression[J].Proceedings of IEEE International Conference on Acoustics,Speech,and Signal Processing,1999:1765-1768

(编辑：戴春秋)

Simultaneous inversion on elastic and physical properties of reservoirbased on Hampel’s three-part redescending function

LI Zhiyong1,ZHANG Jiashu2,CAI Hanpeng1,HU Guangmin1

(1.SchoolofCommunicationandInformationEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,China;2.SichuanKeyLabofSignalInformationProcessing,SouthwestJiaotongUniversity,Chengdu610031,China)

The discrepancies between geophysical measurements and forward modeling data are commonly modeled as Gaussian errors by conventional seismic inversion methods.However,misfit functions constructed by this distribution always have good inversion result in specified regions but have weak adaptability.We assume Gaussian distribution with additional impulse distribution for both seismic noise data and elastic property deviations from the rock-physics model.In this case,Hampel’s three-part redescending estimate function is included in the misfit function,which could perform better to suppress both Gaussian and impulse errors as a robust measure.Minimizing the misfit function classically leads to the Newton’s optimization method,with which elastic and physical properties of reservoir are obtained.This approach can be applied to the areas with different distribution of errors by choosing the degree of threshold.The relative contributions of the rock-physics constraints and prior information are adaptively adjusted,which can increase the stability of the algorithm and ensure a better inversion.Both synthetic and real seismic data examples show that the method can obtain stable and reliable inversion results.

AVO inversion,rock-physics inversion,joint inversion,Gaussian noise,impulse noise,Hampel three-part redescending function

2016-03-03;改回日期：2016-04-26。

李志勇(1985—),男,博士在读,主要从事地震储层反演方面的研究。

胡光岷(1966—),男,教授,现主要从事网络行为学与网络安全、网络体系结构与协议、信号与信息处理技术的应用等方面的研究与教学工作。

国家自然科学基金联合基金项目(U1562218)资助。

P631

A

1000-1441(2017)02-0261-12

10.3969/j.issn.1000-1441.2017.02.013

This research is financially supported by the Joint Funds of the National Natural Science Foundation of China (Grant No.U1562218).

李志勇,张家树,蔡涵鹏,等.基于Hampel三截尾函数的储层弹性和物性参数同步反演[J].石油物探,2017,56(2):-272

LI Zhiyong,ZHANG Jiashu,CAI Hanpeng,et al.Simultaneous inversion on elastic and physical properties of reservoir based on Hampel’s three-part redescending function[J].Geophysical Prospecting for Petroleum,2017,56(2):-272