等效孔隙裂缝介质的弹性阻抗及广义流体因子分析

窦喜英,王恩利,闫国亮,陈启艳,董雪华,潘宇航

(1.中国地震局兰州地震研究所,甘肃兰州730000;2.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020)



等效孔隙裂缝介质的弹性阻抗及广义流体因子分析

窦喜英1,王恩利2,闫国亮2,陈启艳2,董雪华2,潘宇航1

(1.中国地震局兰州地震研究所,甘肃兰州730000;2.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020)

考虑到裂缝介质的双重孔隙特征,将Thomsen等效孔隙裂缝模型与线性滑动模型进行等价对比,得出Thomsen裂缝模型的广义各向异性参数并将其引入到HTI介质的纵波、转换横波弹性阻抗公式中,最终得到对应Thomsen裂缝介质的弹性阻抗公式,建立裂缝参数、岩性参数以及物性参数与弹性阻抗的直接函数关系,对弹性阻抗归一化后进行数值模拟。模拟结果表明,裂缝型油气藏弹性阻抗对裂缝填充物性质极其敏感,且在不同流体饱和条件下对基岩的横纵波速度平方比、基质孔隙度的响应程度差异显著。在此基础上,将各向同性介质流体因子定义延伸,建立适用于各向异性介质的广义流体因子。数值模拟和实际数据处理结果表明,优选的因子能够更好地识别等效孔隙裂缝介质中的流体。

裂缝介质;弹性阻抗;流体识别因子;各向异性参数;柔量

弹性阻抗是重要的叠前储层预测参数之一。自1999年CONNOLY提出各向同性介质纵波弹性阻抗概念[1]以来,弹性阻抗理论得到迅速发展,一系列具有明显物理意义的概念被相继推出,如:VERWEST等提出的射线弹性阻抗(VEI)[2];WHITCOMBE等提出的归一化弹性阻抗[3]、扩展性弹性阻抗(EEI)[4];马劲风提出的广义弹性阻抗(GEI)[5]、反射率阻抗(RI)[6]、Zoeppritz弹性阻抗(ZEI)[7];SANTOS等提出的射线弹性阻抗(REI)[8];苑春芳等对WHITCOMBE的扩展弹性阻抗进行改进得到的新弹性阻抗[9]等。在弹性阻抗理论发展的过程中,为解决P-SV转换横波的层位标定和岩性反演问题,LANDRØM等[10]、DUFFAUT等[11]先后提出了横波弹性阻抗(SEI),基于此概念,GONZLEZ[12]推导了以反射横波角度和入射纵波角度为参数的转换横波弹性阻抗(PSEI),MA等[13]基于Zoeppritz方程推导了转换横波弹性阻抗的精确表达形式(PSZEI)。

与此同时,由于裂缝型油气藏逐渐成为重要的剩余油气资源和研究目标之一,各向异性介质的弹性阻抗成为研究热点之一,MARTINS于2002年首先提出了各向异性弹性阻抗概念[14],并在2006年推导了弱各向异性介质的纵波弹性阻抗公式[15],将弹性阻抗分为各向同性与各向异性两部分,分析它们之间的差异,强调了各向异性在弹性阻抗反演中所起的重要作用。JLEK[16]基于弱各向异性转换横波反射系数公式,推导出复杂的P-SV波、P-SH波弹性阻抗公式。陈天胜等[17]推导出HTI介质的纵波弹性阻抗公式。刘前坤[18]基于Cherepanov的HTI介质PS波反射系数公式,引入Thomsen等效各向异性参数,推导了HTI介质中PS波弹性阻抗公式,并进行了含有不同流体介质的弹性阻抗讨论。CUI等[19]基于简化的Jílek反射系数公式,重新推导了新的各向异性转换波弹性阻抗公式。王恩利等[20]基于Ruger的HTI介质PP波反射系数公式,引入裂缝密度参数化的各向异性参数,推导出包含裂缝参数的弹性阻抗公式。阻抗分析与流体识别密不可分。对AVO信息以及多波多分量地震资料的深入研究推动了储层流体识别技术的发展。基于各向同性介质理论,国内外许多学者提出很多流体指示因子和识别方法,如:GOODWAY等[21]提出了流体识别异常的LMR法;HEDLIN[22]提出了孔隙模量法;RUSSELL等[23]提出了流体组分识别的Russell法;DILLON等[24]提出了直接油气指示(DHI)的波阻抗差分法;陈遵德等[25]提出了利用纵、横波速度，密度以及一些其它地震属性实现岩性油气藏储层预测的方法;黄绪德[26]提出了泊松比流体识别因子;宁忠华等[27]提出了由波阻抗量纲的0次幂和2次幂组合而成的具有较高灵敏度的流体识别因子;尹川等[28]研究了流体因子的敏感性,利用不同敏感程度的流体因子交会分析对流体的识别效果;王栋等[29-30]考虑到波阻抗的高次量纲能将不同含流体砂岩的差异放大,构建了包含有波阻抗量纲4次方的高灵敏度流体识别因子,又于2009年对该流体因子进行修改,增加对流体敏感的λρ项,得到新流体识别因子,取得了良好的效果;许平等[31]提出了类似于王栋等2008年给出的流体识别因子的新流体因子;PEI等[32]联合K/μ,λ/μ两个参数,提出了可以有效识别低孔渗储层中流体的新流体因子λK/μ2;郑静静等[33]综合流体因子ρf和泊松阻抗PI的优点,构建了新的流体因子,更好地提高了抗噪性能和流体检测能力。

传统的裂缝储层弹性阻抗研究多基于静态等效介质理论,由于未充分考虑岩石孔隙和流体,与地下介质的真实情况依然有较大差距,理论误差较大。本文将Thomsen等效多孔裂缝介质模型(低频条件下)的广义各向异性参数引入HTI介质的PP波、P-SV波弹性阻抗公式中,建立裂缝参数、基质孔隙度和弹性阻抗之间的显性关系式,分析裂缝密度、裂缝填充物、基岩的纵横波速度比、基质孔隙度对弹性阻抗的影响,以避免由各向异性参数向裂缝参数和基质孔隙度参数转换中引入的误差。此外,在继承前人研究成果的同时,尝试将流体因子引入到等效孔隙裂缝介质中,研究裂缝参数、基质孔隙度、入射角和方位角对流体因子的影响。

1 等效裂缝介质理论

根据等效介质理论,许多研究者提出了多种HTI介质模型,常用的主要有3类:孤立平行薄扁平裂缝模型(Hudson裂缝模型)[34]、线性滑动模型[35]和等效孔隙裂缝模型[36-37]。其中,等效孔隙裂缝模型中孔隙和裂缝连通,处于前两种模型的中间状态。该模型假定裂缝为硬币状,平行排列且稀疏分布于由均匀颗粒构成的多孔介质中。不同频带条件下流体影响因子不同,导致了各向异性参数值有差异。低频带内,裂缝与相邻孔隙间的流体保持局部压力均衡,即裂缝间的流体通过孔隙可以互相流通;高频带内,裂缝间的流体不能相互流通,即各个裂缝独立且相互没有影响。地震频带属于低频带,是我们研究最多的频带范围,在这种低频限制下,如果基质孔隙度较低(φp<10%),那么如同模拟平行裂缝一样,可以将介质模型中的孔隙看作少量集中分布,即介质的基质孔隙可模拟成各向同性固体背景中的球体稀疏分布,本文将这种低频裂缝模型称为等效孔隙裂缝模型,将其与线性滑动模型等价比较后建立的新柔量表达式引入以柔量为参数的广义各向异性参数[38]中,得到新广义各向异性参数关系式:

(1)

(2)

(3)

(4)

式中:ε(V)表示P波各向异性程度;δ(V)表示P波在横向和垂向之间各向异性变化的快慢程度;γ(V)表示快、慢横波的速度差异程度;η(V)表示模型非椭圆率程度;e为裂缝密度(单位体积内裂缝的数量);g为横纵波速度平方比;q是与流体相关的系数[38],且q=(1-Kf/Kb)Dcp,其中,Kf为流体体积模量,Kb为基岩体积模量,Dcp为流体影响因子。

显然,由于孔隙的存在,使得广义各向异性参数变得较为复杂。公式中,γ(V)不受填充流体性质的影响,并与裂缝密度e呈线性关系;参数ε(V),δ(V)和η(V)除与裂缝密度e和横纵波速度平方比g有关外,还与q系数中的基质孔隙度φp和裂缝填充物相关,而对q系数中的纵横比(c/a,即裂缝厚度/裂缝直径)不敏感[27]。

从以上分析可以推论,裂缝填充物、裂缝密度、围岩的横纵波速度比、基质孔隙度是直接影响裂缝介质各向异性参数的因素,而作为裂缝型油气藏检测的重要指标,它们必将对各向异性弹性阻抗产生显著影响。本文将所推导的广义各向异性参数关系式((1)式～(4)式)引入到裂缝介质弹性阻抗公式中,进行数值模拟,探索对各向异性参数有影响的几种因素变化时等效孔隙裂缝介质弹性阻抗的变化规律。

2 等效孔隙裂缝介质弹性阻抗

2.1 弹性阻抗

将等效孔隙裂缝介质的广义Thomsen各向异性参数关系式((1)式～(4)式)代入陈天胜等[17]推导的HTI介质PP波弹性阻抗公式中,整理得到等效孔隙裂缝介质的PP波弹性阻抗公式:

(5)

式中:α为纵波速度;β为横波速度;ρ为密度;φ为方位角;θ为入射角;k=β/α。

(5)式中的q与(1)式中的q相同,将q中所有的Kf用气体体积模量(Kf=0.02GPa)替代,则(5)式变为气饱和裂缝介质的弹性阻抗,而用水体积模量(Kf=2.00GPa)代替,则(5)式为水饱和裂缝介质的弹性阻抗。

同理,将(1)式～(4)式代入到HTI介质P-SV波弹性阻抗公式[19]中,整理得到等效孔隙裂缝介质的P-SV波弹性阻抗公式:

(6)

其中,

分别把气和水的体积模量代入到公式(6)中,能够得到气饱和与水饱和裂缝介质的P-SV波弹性阻抗。

2.2 数值模拟

选用HILTERMAN[39]的第1类AVO气砂岩作为背景参数,修改砂岩为等效孔隙裂缝介质,在裂缝密度e(模型①)、基质孔隙度φp(模型②)、横纵波速度平方比g(模型③)3方面进行参数改造,并考虑水饱和与气饱和条件的影响(见表1),开展PP波和P-SV波弹性阻抗的数值模拟,具体步骤为:①计算每种改造对应的归一化各向同性弹性阻抗;②计算气饱和与水饱和等效孔隙裂缝介质的归一化弹性阻抗;③将步骤②中弹性阻抗结果与步骤①中相应的各向同性弹性阻抗结果做差,得到相应流体饱和状态下裂缝介质的阻抗差。

模拟结果的组织方式参考表1,得到PP波的阻抗差(图1)和P-SV波的阻抗差(图2)。其中,图1a,图1d和图2a,图2d讨论模型①中裂缝密度为0.05,0.10和0.15时的响应;图1b,图1e和图2b,图2e讨论模型②中基质孔隙度φp为0.001,0.010和0.100时的响应;图1c,图1f和图2c,图2f讨论模型③中横纵波速度平方比g为0.25,0.36和0.49时的响应。每张图中从上到下的曲面对应参数从小到大的变化。

表1 双层模型介质参数设置

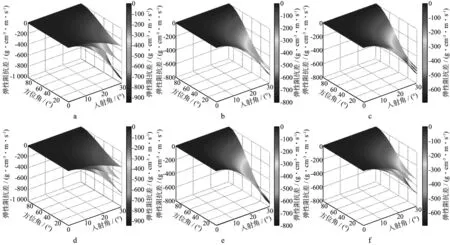
图1 气饱和(a,b,c)与水饱和(d,e,f)等效孔隙裂缝介质的PP波阻抗差a,d 模型①,e=0.05,0.10,0.15; b,e 模型②,φp=0.001,0.010,0.100; c,f 模型③,g=0.25,0.36,0.49

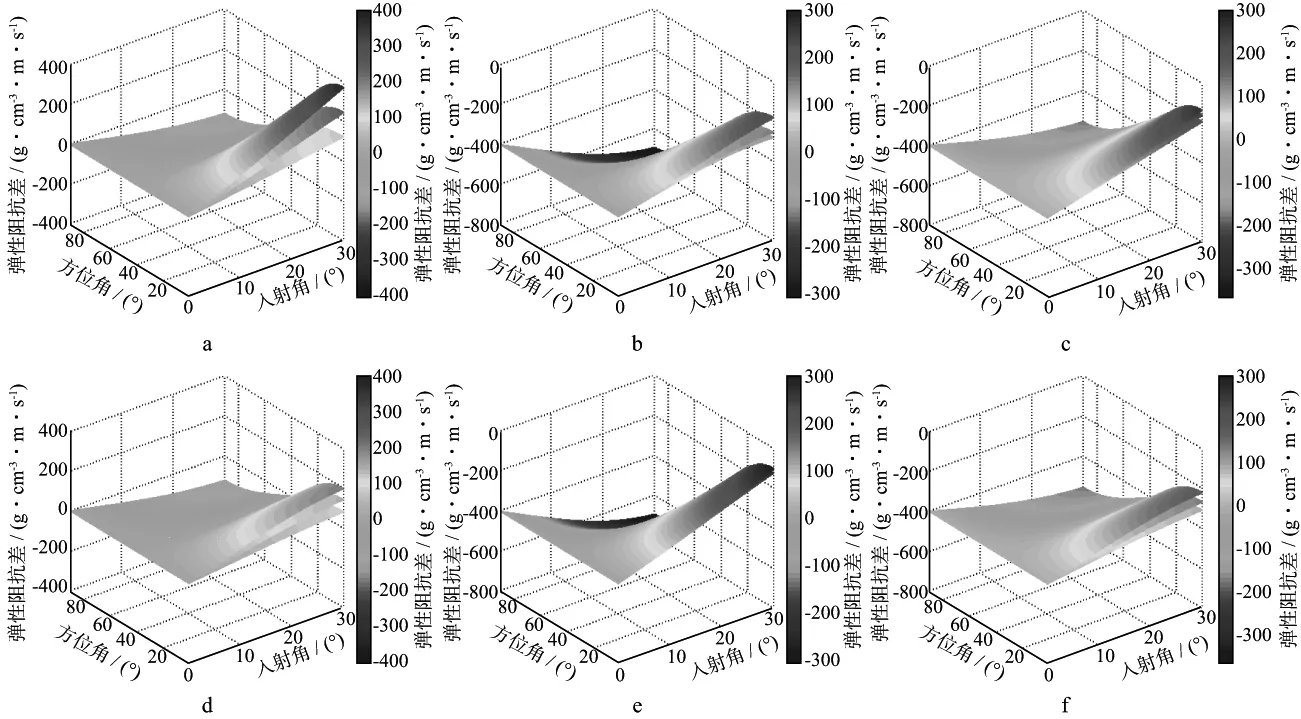
图2 气饱和(a,b,c)与水饱和(d,e,f)等效孔隙裂缝介质的P-SV波阻抗差a,d 模型①,e=0.05,0.10,0.15; b,e 模型②,φp=0.001,0.010,0.100; c,f 模型③,g=0.25,0.36,0.49

为分析阻抗的方位各向异性,进一步抽取在入射角θ=30°,方位角φ∈(0,360°)时相应PP波和P-SV波阻抗差绝对值，在极坐标中的显示如图3和图4所示,其中,图3a,图3d和图4a,图4d对应模型①的裂缝密度e参数变化响应;图3b,图3e和图4b,图4e对应模型②的等径孔隙度φp参数变化响应,图3c,图3f和图4c,图4f对应模型③的横纵波速度平方比g参数变化响应,蓝、绿和红色曲线代表对应参数依次增大。

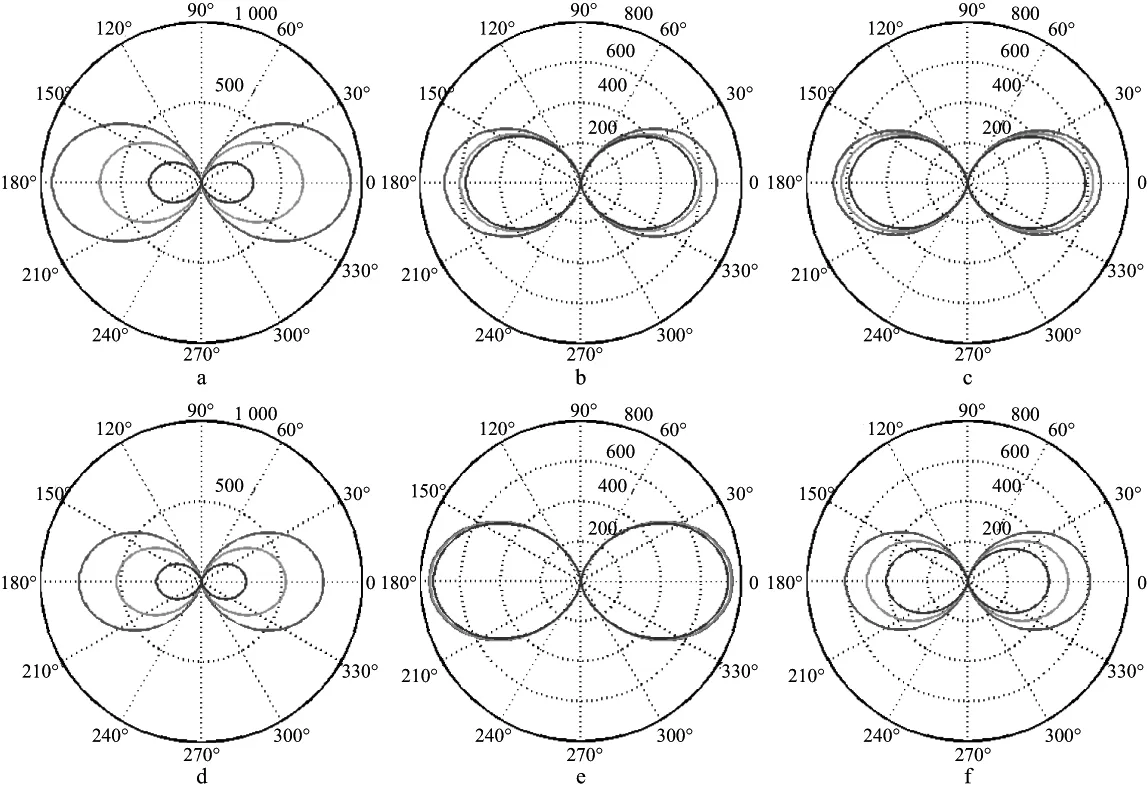
图3 气饱和(a,b,c)与水饱和(d,e,f)等效孔隙裂缝介质的PP波阻抗差极坐标(θ=30°,φ∈(0,360°))a,d 模型①,e=0.05,0.10,0.15; b,e 模型②,φp=0.001,0.010,0.100; c,f 模型③,g=0.25,0.36,0.49

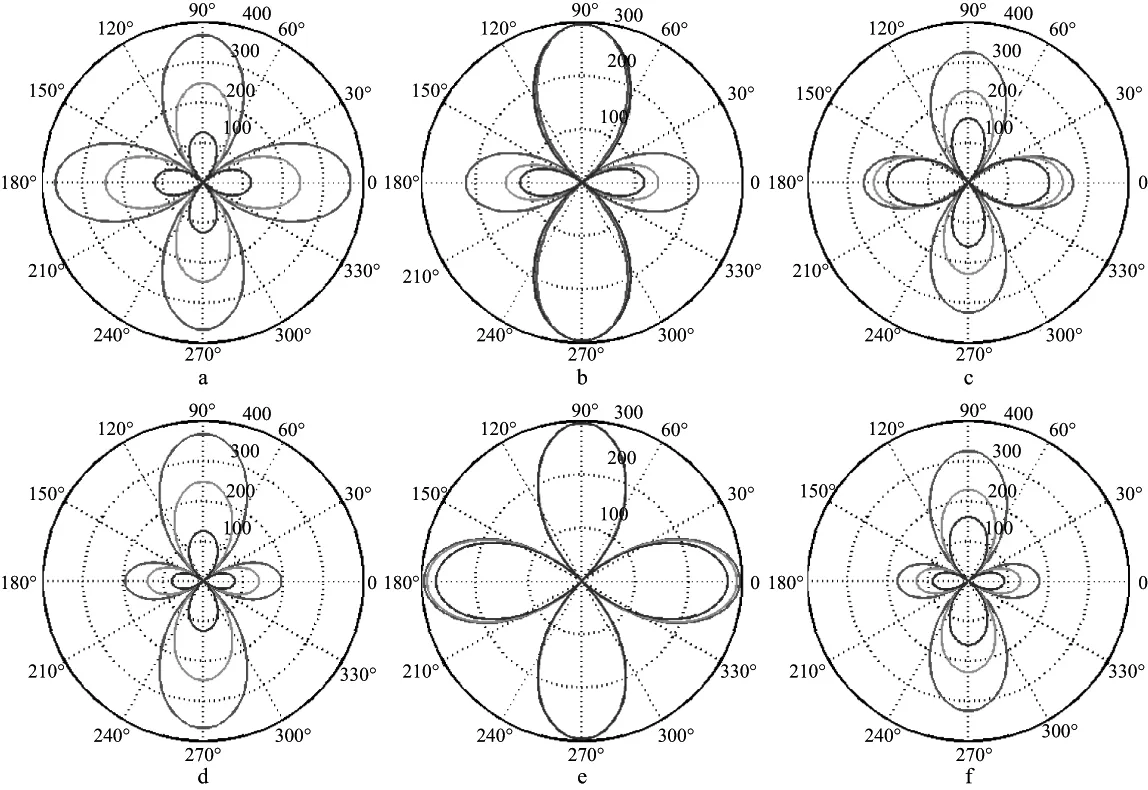
图4 气饱和(a,b,c)与水饱和(d,e,f)等效孔隙裂缝介质的P-SV波阻抗差极坐标(θ=30°,φ∈(0,360°))a,d 模型①,e=0.05,0.10,0.15; b,e 模型②,φp=0.001,0.010,0.100; c,f 模型③,g=0.25,0.36,0.49

综合分析图1～图4,总结如下。

1) PP波、P-SV波阻抗差随着入射角、方位角的变化呈现周期性的方位各向异性特征，但有所区别。区别之一:曲线、曲面形态。PP波阻抗差方位角在垂直裂缝面方向(0和180°)的相邻区域内,阻抗差幅值最大,各向异性最强,方位角在平行裂缝面方向(±90°)的相邻区域内,阻抗差为0,即各向同性。而P-SV波阻抗差呈4片花瓣状,方位角在垂直裂缝面方向(0和180°)和平行裂缝面方向(90°,270°)的相邻区域内,都具有方位各向异性差异;在平行裂缝面方向,同一参数变化情况下,气、水饱和状态下阻抗差幅值相等;在垂直裂缝面方向,阻抗差幅值存在显著的梯度变化,是P-SV波阻抗差各向异性差异性的主要来源。区别之二:阻抗差数值分布。PP波阻抗差始终为负,且在单一象限内数值幅度随方位角和入射角的增大呈现稳定的单调递增特征,这表明HTI介质PP波阻抗在数值上小于各向同性阻抗。而P-SV波阻抗差随入射角、方位角变化会出现符号反转现象,换言之P-SV波各向异性阻抗值不总是低于各向同性阻抗。

2) 裂缝密度是影响阻抗的最重要因素,无论是气饱和还是水饱和条件下,由裂缝密度引起的阻抗差变化幅度都要高于基质孔隙度和横纵波速度平方比参数。另外,对比图1,图2,图3和图4中左侧图可见,PP波、P-SV波阻抗差均随裂缝密度增大而增大,其中,PP波为负向,P-SV波为正向。对比阻抗差的幅值,可见气饱和状态均高于水饱和状态。

3) 横、纵波速度平方比对阻抗的影响程度略弱于裂缝密度。对比图1,图2,图3和图4中的右侧图可见,PP波、P-SV波阻抗差均随速度平方比的增大而增大,其中,PP波为负向,P-SV波为正向。对比阻抗差幅值的梯度变化可见,PP波阻抗差在气饱和状态下均弱于水饱和状态,而P-SV波阻抗差的变化恰恰相反,在气饱和状态下强于水饱和状态。

4) 基质孔隙度是阻抗的另外一个影响因素,对比图1,图2,图3和图4中的中间图可见,在孔隙介质中,随着基质孔隙度的增加,PP波、P-SV波阻抗差均有增大的趋势,且气饱和条件下的阻抗差梯度变化更加显著。

可见,阻抗差可明显区分填充物性质,识别介质中含气或含水性。裂缝密度、基质孔隙度或横纵波速度平方比的变化对于区分裂缝型储层的填充物性质也具有很好的优势。

3 广义流体因子构建及敏感性分析

以声波的纵波、横波阻抗组合而成的几种常见流体识别因子主要有：GOODWAY等[21]构建的λρ和μρ,RUSSELL等[23]构建的ρf,宁忠华等[27]构建的σHSFIF和σHSFIF1,王栋等[29-30]构建的FIFW和F1,以及许平等[31]构建的FIFP。为实现裂缝型介质的流体识别,尝试用裂缝介质的纵波和转换横波的弹性阻抗替代这几种常见流体因子公式中的纵波和横波阻抗,将裂缝密度、入射角和方位角参数引入流体因子中,形成广义流体识别因子,形式如下:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

上述公式中的c,B和C均为调节参数,c的取值范围为1.33～3.00,其具体大小需根据所研究的储层特性而定,B的大小与岩性有关,C值一般取2.8即可明显区分气、水砂岩。

以HILTERMAN[39]给出的第1类砂岩参数(表2) 作为双层介质的背景参数,将下层砂岩修改为等效孔隙裂缝介质,取裂缝密度e=0.1,进行不同流体饱和状态下介质的PP波和P-SV波弹性阻抗计算,进而获得几种广义流体因子,探讨它们对裂缝介质流体识别的适用性。

表2 模型背景参数

抽取入射角θ=30°,方位角φ∈(0,360°)时的流体因子曲线如图5所示,图中增加gIPP,gIP-SV以示表明纵波、转换横波弹性阻抗作为流体指示因子效果很差,不提倡直接用于流体识别。gμρ在水、气两种饱和状态下差异不明显,而gλρ差异较显著,这与宁忠华等[27]的观点一致。gF1突跳点太多且值很大,无法实现整体方位角范围的流体识别,不适于裂缝介质模型,其它广义流体因子气、水饱和差异较大。

由上述可见,gμρ,gλρ,gρf,gσHSFIF,gσHSFIF1,gFIFW和gFIFP均适用于裂缝介质的流体识别,为比较灵敏度差异性,引入一个相对差异参数,即水、气饱和状态下流体因子之差的绝对值除以两者之和的绝对值,相对差异值越大,说明其流体识别的灵敏度越高。设裂缝密度不变,固定方位角φ=0,30°,45°,60°,75°,90°,得到这些广义流体因子的相对差异随入射角变化(θ∈(0,30°))曲线如图6所示;固定入射角θ=10°,20°,30°,则广义流体因子之间的相对差异随方位角变化(φ∈(0,30°))的曲线如图7所示。图6中,φ=90°为各向同性面,不含流体,流体因子相对差异为零,φ=60°和φ=75°时相对差异曲线基本相近,只保留其中一个进行讨论即可。综合分析图6中φ=0,30°,45°,60°的曲线与图7,根据灵敏度差异程度,可将流体因子gFIFW和gFIFP归为一类,记为第1类灵敏度流体因子,gρf和gσHSFIF归为一类,记为第2类灵敏度流体因子,gλρ和gσHSFIF1归为一类,记为第3类灵敏度流体因子;gμρ流体因子相对差异值不超过0.05,灵敏度非常低,单独用以识别流体效果极差。

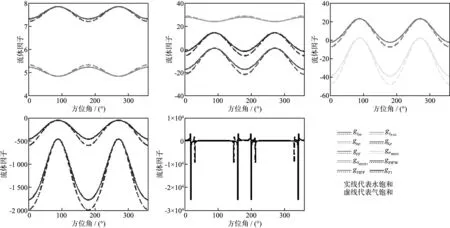
图5 不同流体因子的流体识别对比(θ=30°,φ∈(0,360°))

图6 气、水饱和裂缝介质流体因子之间的相对差异随入射角变化的曲线

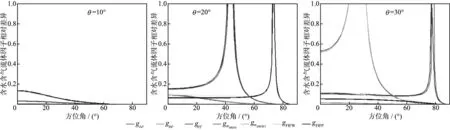
图7 气、水饱和裂缝介质流体因子之间的相对差异随方位角变化的曲线

虽然3类灵敏度流体因子均可明显区分介质中的流体性质,但顾及到在方位角和入射角两种范围内相对差异值的覆盖程度,我们认为第1类灵敏度流体因子最佳,即gFIFW区分流体的能力更强。为验证这一观点,下面以实际数据为例，分析这3类灵敏度流体因子的识别效果，探讨最优灵敏度流体因子。

4 应用实例

已知某工区的测井曲线如图8所示,深度在5046m以上的地层为各向同性层,在5046～5048m为干层,裂缝密度为0.03,5048m以下为含气层,裂缝密度为0.20。将gFIFW,gσHSFIF和gσHSFIF1这3类流体因子应用于该测井数据处理中,并与相应常规流体因子进行对比,结果如图9所示,蓝色曲线代表入射角和方位角均为30°时的广义流体因子,红色曲线代表常规流体因子。从图9中可知,广义因子与常规因子的曲线形态基本相似,说明使用广义流体因子进行流体识别具有较高可信度;常规流体因子FIFW,σHSFIF和σHSFIF1基本无法区分干层和含气层,而广义流体因子从气层上界面(5048m)开始出现明显的变化;对比3类广义流体因子与对应常规流体因子可知,在气层,gFIFW与对应常规流体因子的差异性最大,gσHSFIF次之,gσHSFIF1差异性最小,由此验证了推导公式((7)式～(14)式)的正确性。

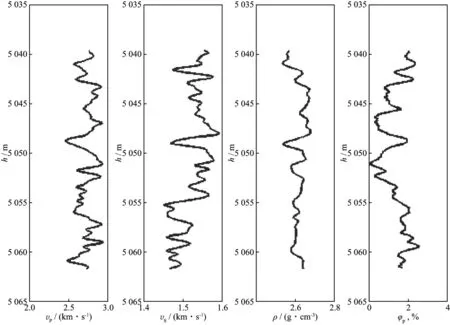
图8 测井曲线

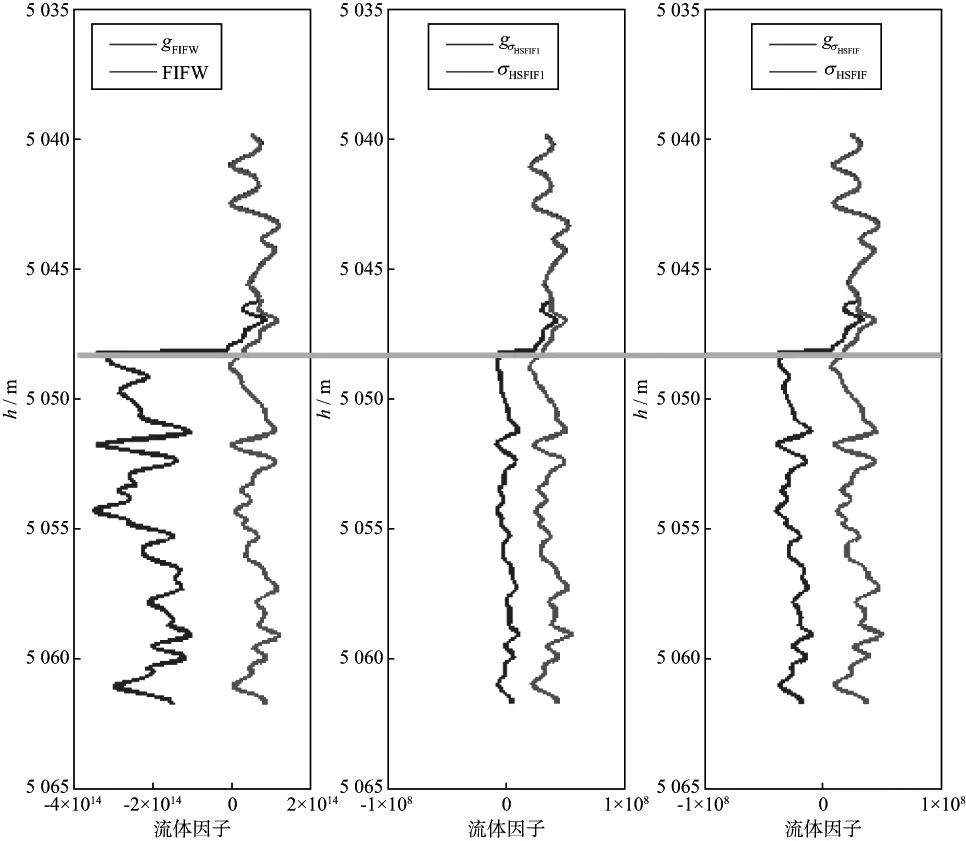
图9 广义流体因子与常规流体因子的流体识别效果对比(淡蓝色横线为干层/气层分界线)

5 结论

裂缝流体识别研究是剩余油气研究的重要领域之一。本文借助等效裂缝模型中“柔量参数”这个桥梁架起了等效孔隙裂缝模型中裂缝参数、基质孔隙度与广义各向异性参数之间的关系,建立了新的弹性阻抗与流体因子,并对其中的关键参数,包括裂缝密度、横纵波速度比和基质孔隙度进行数值模拟讨论,所得结论如下:

1) 等效孔隙裂缝介质的纵波、转换横波弹性阻抗呈现明显的方位各向异性,且两者差异明显;在垂直裂缝方向,两者都具有明显的方位性,而沿裂缝方向转换横波存在方位各向异性,纵波不具有这一特点;

2) 裂缝密度、基质孔隙度或横纵波速度平方比等参数变化引起的阻抗差变化,可以用于区分裂缝型储层的填充物性质,其中裂缝密度和基质孔隙度引起含气介质的阻抗差变化高于含水介质,横纵波速度平方比引起的变化则相反;

3) 流体因子源于纵、横波弹性阻抗,由裂缝介质的转换横波弹性阻抗单独形成的流体因子gμρ不适用于介质中的流体识别;

4) 将常规流体因子延伸的裂缝介质流体因子按流体识别灵敏程度归为3类,其中gFIFW>gσHSFIF≈gσHSFIF1,实际数据处理中具有很好的适用性。

等效裂缝介质理论作为裂缝介质的一种近似理论,更加接近于地下的真实介质,那么对于该类介质的PP波、P-SV波弹性阻抗以及流体识别因子的研究非常有意义。本文基于较低孔隙度的等效裂缝介质模型进行PP波、P-SV波弹性阻抗正演模拟研究,其原因在于这种情况下模型弹性矩阵相对简单,而高孔隙度裂缝介质模型引入的参数多而复杂,形成的弹性矩阵为裂缝介质的弹性阻抗研究增加了困难,有待后期深入研究。

将各向同性介质的流体识别因子延伸到各向异性介质,包含方位角信息后增加了流体因子分析的直观性,拓宽了流体因子的应用范围,对流体因子的灵敏度归类以及归类后的灵敏程度对比可以避免后期盲目的乱用流体因子进行流体识别,但本文只对常用的9个流体因子进行分析,各向同性介质的其它流体识别因子是否适合于裂缝介质还有待继续分析。

[1] CONNOLY P.Elastic impedance[J].The Leading Eage,1999,18(4):438-452

[2] VERWEST B J,MASTERS R,SENA A.Elastic impedance inversion[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000:1580-1582

[3] WHITCOMBE D N.Elastic impedance normalization[J].Geophysics,2002,67(1):60-62

[4] WHITCOMBE D N,CONNOLLY P A,REAGAN R L,et al.Extended elastic impedance for fluid and lithology prediction[J].Geophysics,2002,67(1):63-67

[5] 马劲风.地震勘探中广义弹性阻抗的正反演[J].地球物理学报,2003,46(3):118-124 MA J F.Forward modeling and inversion method of generalized elastic impedance in seismic exploration[J].Chinese Journal of Geophysics,2003,46(3):118-124

[6] MA J F,MOROZOV I B.Ray-path elastic impedance[J].CSEG 2004 Annual Meeting Abstracts,2004:10-12

[7] MA J F,MOROZOV I B.The exact elastic impedance[J].CSEG 2005 Annual Meeting Abstracts,2005:224-227

[8] SANTOS L T,TYGEL M.Impedance-type approximation of the P-P elastic reflection coefficient:modeling and AVO inversion[J].Geophysics,2004,69(2):592-598

[9] 苑春方,彭苏萍,吕焱,等.Whitcombe扩展弹性阻抗公式的改进[J].岩土力学,2009,30(12):3710-3714 YANG C F,PENG S P,LU Y,et al.Improvement of Whitcombe’s extended elastic impedance formula[J].Rock and Soil Mechanics,2009,30(12):3710-3714

[10] LANDRØM,DUFFAUT K,ROGNO H.Well calibration of seabed seismic data[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999:860-863

[11] DUFFAUT K,ALSOS T,LANDRØM,et al.Shear wave elastic impedance[J].The Leading Edge,2000,19(11):1222-1229

[13] MA J F,MOROZOV I B.The exact elastic impedance for P-SV wave[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:288-292

[14] MARTINS J L.An approach for elastic impedance in weakly anisotropic media[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002:185-188

[15] MARTINS J L.Elastic impedance in weakly anisotropic media[J].Geophysics,2006,71(3):D73-D83

[17] 陈天胜,魏修成,刘洋.一种新的各向异性弹性阻抗近似公式[J].石油物探,2006,45(6):563-569 CHEN T S,WEI X C,LIU Y.New approximation formula for calculation of elastic impedance in anisotropic media[J].Geophysical Prospecting for Petroleum,2006,45(6):563-569

[18] 刘前坤.方位各向异性介质AVO及弹性波阻抗研究[D].长春:吉林大学,2008 LIU Q K.Study on AVO and elastic impedance of azimuthal anisotropic media[D].Changchun:Jilin University,2008

[19] CUI J,HAN L G,LIU Q K,et al.P-SV wave elastic impedance and fluid identification factor in weakly anisotropic media[J].Applied Geophysics,2010,7(2):135-142

[20] 王恩利,陈启艳,窦喜英.裂缝型 HTI 介质的纵波弹性阻抗[J].地球物理学进展,2012,27(1):263-270 WANG E L,CHEN Q Y,DOU X Y.P-wave elasic impedance in fractured HTI media[J].Progress in Geophysics,2012,27(1):263-270

[21] GOODWAY W,CHEN T,DOWNTON J.Improved AVO fluid detection and lithology discrimination using Lame petrophysical parameters from P and S inversion[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997:183-186

[22] HEDLIN K.Pore space modulus and extraction using AVO[J].SEG Technical Program Expanded Abstracts,2000,29(19):1690-1692

[23] RUSSELL B H,HEDLIN K,HILTERMAN F J,et al.Fluid property discrimination with AVO:a Biot-Gassmann perspective[J].Geophysics,2003,68(1):29-39

[24] DILLON L,SCHWEDERSKY G,GUILHERME V,et al.A multiscale DHI elastic attributes evaluation[J].The Leading Edge,2003,22(10):1024-1029

[25] 陈遵德,朱广生.地震储层预测方法研究进展[J].地球物理学进展,1997,12(4):76-84 CHEN Z D,ZHU G S.Research progress on the method of seismic reservoir prediction[J].Progress in Geophysics,1997,12(4):76-84

[26] 黄绪德.油气预测与油气藏描述:地震勘探直接找油气[M].南京:江苏科学技术出版社,2003:35-37 HUANG X D.Hydrocarbon prediction and reservoir description:direct hydrocarbon detection via seismic prospecting[M].Nanjing:Jiangsu Science & Technology Press,2003:35-37

[27] 宁忠华,贺振华,黄德济.基于地震资料的高灵敏度流体识别因子[J].石油物探,2006,45(3):239-241 NING Z H,HE Z H,HUANG D J.High sensitive fluid identification based on seismic data[J].Geophysical Prospecting for Petroleum,2006,45(3):239-241

[28] 尹川,顾汉明.流体指示因子的敏感性分析[J].工程地球物理学报,2008,5(1):85-88 YIN C,GU H M.The sensitivity analysis of AVO fluid factors[J].Chinese Journal of Engineering Geophysics,2008,5(1):85-88

[29] 王栋,贺振华,黄德济.含气含水砂岩的高灵敏度流体识别因子的研究[J].长江大学学报(自然科学版),2008,5(3):45-47 WANG D,HE Z H,HUANG D J.Research of high sensitive fluid identifying factor in water containing sandstone[J].Journal of Yangtze University (Nat Sci Edit),2008,5(3):45-47

[30] 王栋,贺振华,黄德济.新流体识别因子的构建与应用分析[J].石油物探,2009,48(2):141-145 WANG D,HE Z H,HUANG D J.Construction of a new fluid identification factor and analysis on its application[J].Geophysical Prospecting for Petroleum,2009,48(2):141-145

[31] 许平,文晓涛,雷芬丽.高灵敏度流体因子识别研究[J].长江大学学报(自然科学版),2010,7(3):221- 222 XU P,WEN X T,LEI F L.Study on high sensitive fluid identifying factor[J].Journal of Yangtze University (Nat Sci Edit),2010,7(3):221-222

[32] PEI F G,ZOU C C,HE T.Fluid sensitivity study of elastic parameters in low-medium porosity and permeability reservoir rocks[J].Applied Geophysics,2010,7(1):1-9

[33] 郑静静,印兴耀,张广智.流体因子关系分析以及新流体因子的构建[J].地球物理学进展,2011,26(2):579-587 ZHENG J J,YIN X Y,ZHANG G Z.Fluid factor analysis and the construction of the new fluid factor[J].Progress in Geophysics,2011,26(2):579-587

[34] HUDSON J A.Overall properties of a cracked solid[J].Mathematical Proceedings of the Cambridge Philosophical Society,1980,88(2):371-384

[35] SCHOENBERG M.Reflection of elastic waves from periodically stratified media with interfacial slip[J].Geophysical Prospecting,1983,31(2):265-292

[36] THOMSEN L.Elastic anisotropy due to aligned cracks in porous rock[J].Geophysical Prospecting,1995,43(6):805-829

[37] HUDSON J A,LIU E,CRAMPIN S.The mechanical properties of materials with interconnected cracks and pores[J].Geophysical Journal International,1996,124(1):105-112

[38] BAKULIN A,GRECHKA V,TSVANKIN I.Estimation of fracture parameters from reflection seismic data-part I:HTI model due to a single fracture set[J].Geophysics,2000,65(6):1788-1802

[39] HILTERMAN F J.Seismic amplitude interpretation:SEG/EAGE distinguished instructor series no.4[M].USA:Society of Exploration Geophysicists,2001:102-114

(编辑：顾石庆)

The analysis on elastic impedance and generalized fluid factor inequivalent porous fracture media

DOU Xiying1,WANG Enli2,YAN Guoliang2,CHEN Qiyan2,DONG Xuehua2,PAN Yuhang1

(1.LanzhouInstituteofSeismology,ChinaEarthquakeAdministration,Lanzhou730000,China;2.PetroChinaResearchInstituteofPetroleumExploration&DevelopmentNorthwest,Lanzhou730020,China)

Considering double porosity features of fracture media,generalized anisotropic parameters obtained in the Thomsen equivalent porous media model,equivalent to linear slip model are introduce into P-wave and P-SV-wave elastic impedance equations in HTI media,and the elastic impedance formula corresponded to Thomsen fracture media is obtained.The direct function relation between fracture,lithology,physical property parameters and elastic impedance is established.Numerical simulation show that the elastic impedance of fractured reservoirs is very sensitive to the properties of fracture fillings,its response degree to (vS/vp)2and equant matrix porosity is significantly different.Based on this,a generalized fluid factor suitable for the anisotropic media is established by extending the isotropic media fluid factor.The test results of numerical simulation and actual data processing results indicate that the generalized fluid factor can accurately identify the fluid in equivalent porous fracture media.

fracture media,elastic impedance,fluid identification factor,anisotropic parameter,weaknesses

2016-07 -01;改回日期：2016-10-31。

窦喜英(1980—),女,博士,主要从事地球物理学和地震预报研究。

中国地震局兰州地震研究所地震科技发展基金项目(2016050)和中国石油天然气股份有限公司科学研究与技术开发项目(2015B-3712)共同资助。

P631

A

1000-1441(2017)02-0192-11

10.3969/j.issn.1000-1441.2017.02.005

This research is financially supported by the Earthquake Science and Technology Development Fund of China Earthquake Administration of Gansu Province (Grant No.2016050) and the Science Research and Technology Development Project of PetroChina Co. Ltd. (Grant No.2015B-3712).

窦喜英,王恩利,闫国亮,等.等效孔隙裂缝介质的弹性阻抗及广义流体因子分析[J].石油物探,2017,56(2):-202

DOU Xiying,WANG Enli,YAN Guoliang,et al.The analysis on elastic impedance and generalized fluid factor in equivalent porous fracture media[J].Geophysical Prospecting for Petroleum,2017,56(2):-202