基于White模型的含气砂岩垂直入射地震响应特征分析

李世凯,文晓涛,阮韵淇,李 天,张 瑞,张金明

(1.油气藏地质及开发工程国家重点实验室(成都理工大学),四川成都610059;2.成都理工大学地球物理学院,四川成都610059;3.成都理工大学能源学院,四川成都610059)



基于White模型的含气砂岩垂直入射地震响应特征分析

李世凯1,2,文晓涛1,2,阮韵淇1,3,李 天1,2,张 瑞1,2,张金明1,2

(1.油气藏地质及开发工程国家重点实验室(成都理工大学),四川成都610059;2.成都理工大学地球物理学院,四川成都610059;3.成都理工大学能源学院,四川成都610059)

基于空间周期排列的球状斑块饱和模型(White模型)和动态体积模量理论,研究了含气饱和度和渗透率对固结良好、中等固结和未固结砂岩储层地震响应特征的影响,结果表明:①当含气饱和度增大时,地震纵波相速度的衰减会更加明显,在地震频段内可达数百m/s,而渗透率增大对其造成的影响则相对较小;②高频情况下,含气饱和度越高,逆品质因子越高,地震波衰减越强;③低频情况下,含气饱和度越高,逆品质因子越低,地震波衰减越弱。利用相移法波动方程正演对三类砂岩储层地震响应特征进行了数值模拟,结果显示:①增大含气饱和度可使储层下界面反射产生时间延迟,且在未固结和中等固结的砂岩储层中十分明显,地震波主频逐渐向低频方向移动;②在含气饱和度较高的状态下,介质中流体的流动性增强,导致渗透率对地震波速度的衰减能力增强。

斑块饱和模型;含气砂岩;含气饱和度;波动方程正演;渗透率;时间延迟

目前,关于含气储层地震响应特征的研究尚处在探索阶段,而近年来快速发展的岩石物理理论则能够对含流体介质的地球物理特征研究提供理论指导。早在1956年,BIOT就基于弹性波在含流体多孔介质中的传播规律,提出了经典的Biot流体波动理论[1-2],并假设流体运移是能量损失的主要原因。其后,MAVKO等提出了孔隙尺度下的喷射流衰减机制[3]。DVORKIN等将喷射流衰减机制与Biot理论相结合,提出了经典的BISQ理论[4]。WHITE[5]首次对岩石内部的局部非均质性进行了探讨,并由此提出了斑块饱和模型,在中观尺度上对流体流动衰减机制进行了解释。邓继新等[6-7]通过实验室测试,对储层砂岩纵波速度与饱和度的相关性进行了研究,指出斑块模型的速度频散关系与多个孔隙有关。李晓波等[8]利用标准线性体模型对斑块饱和介质的粘弹性特征进行了数值模拟,讨论了地震波衰减和频散特征及孔隙度对地震波形的影响。RUBINO[9]分析了砂岩储层中渗透率对地震响应的影响,指出岩石颗粒相对松散、孔隙较发育的砂岩储层渗透率对地震波的频散和衰减有较大影响。王峣钧等[10]基于周期层状流体饱和模型,利用地震波频散特征对砂岩储层含气性进行了分析。陈程等[11]基于空间周期排列球状斑块饱和模型,研究了砂岩储层渗透率对地震响应特征的影响。

目前基于岩石物理模型的国内外文献中,关于孔隙度对地震响应特征的影响研究较多,而关于渗透率、含气饱和度对地震响应特征的影响研究则较少,且缺乏对不同类型(固结良好、压实、未固结)砂岩储层的分析。在常用的数值模拟方法中,相移法频率-波数域波动方程正演由于运算效率高且能较准确地描述含流体介质的频散特征而备受青睐[12]。本文基于White球状斑块饱和模型,结合实际砂体储层地质特征,讨论了三类经典含气砂岩中地震波相速度和品质因子的频散关系以及二者随渗透率、含气饱和度变化的规律,利用相移法频率-波数域波动方程正演研究了不同含气饱和度对砂岩储层地震响应特征的影响。

1 基本原理

球状斑块饱和模型空间呈椭球体或球体周期排列,且每个球体内部区域为饱含气介质,外部区域为饱含水介质。当地震纵波传播到斑块饱和介质时,由于所含气和水具有不同的物理性质,在孔隙中产生的压力并不均匀。Biot提出的慢波扩散理论能够解释相应的孔隙压力平衡过程。利用地震波在孔隙介质中的运动方程[1],Biot理论给出了地震波的扩散长度L:

(1)

式中:ω为角频率;κ为岩石骨架的渗透率;η为孔隙流体的黏滞系数;Mi,Ki可利用Hill理论和Reuss平均公式根据饱和孔隙介质的物性参数给出[9],其中i=m,s,f分别代表干岩石、固体颗粒和流体的等效P波模量和体积模量。此外有:

(2)

当地震波频率足够低时,根据公式(1),L远大于介质中孔隙的长度,孔隙中的流体有足够的时间来达到动态压力平衡,因此可由Wood定律得到孔隙流体的有效体积模量KR:

(3)

式中:Kf,i为孔隙所含不同流体的体积模量;fi为不同流体在介质中所占的体积分量。在斑块饱和模型中,由于所含流体为气和水,因此这里可以将气、水的流体饱和度Sgas和Swater等效为体积分量。若不考虑气体赋存的几何性质,则岩石的等效体积模量在低频背景下可根据Gassmann方程得到:

(4)

相对地,当地震波频率非常高时,扩散长度远小于孔隙的长度,导致孔隙流体之间的压力无法达到平衡状态。根据Hill理论[13]的假设,当混合物各组分的剪切模量相等时,可给出等效P波模量。于是可以得到高频条件下的岩石等效体积模量Kh:

(5)

式中:Si为气或水的饱和度,Ki则为对应流体的体积模量;μ为饱和岩石的剪切模量。

Johnson结合Kh和Kl提出了动态体积模量Kd,可用来估算中间频率时含气、水储层岩石的有效体积模量:

(6)

其中,ξ和τ可由干岩石和流体的物理属性及用于描述孔隙形状特性的Johnson参数得到,具体计算过程参见文献[14]。

由动态体积模量Kd可计算得到地震纵波在含气储层中的复速度:

(7)

式中:ρb=(1-φ)ρs+φ(Sf,iρf,i),i=g,w(气和水)。其中,ρs和ρf,i分别是岩石固体颗粒和流体的密度,φ为孔隙度,Sf,i为流体饱和度。

根据Carcoine衰减机制,利用复速度可求得黏弹性介质中的等效P波相速度和品质因子:

(8)

(9)

为了直观地描述地震波在斑块饱和介质中的响应特征,选用相移法频率-波数域波动方程正演进行数值模拟分析。根据黏弹性介质的二维声波方程:

(10)

式中:U为质点位移;K(ω)为复数体积模量;ρ为介质的密度。若速度在横向上无变化,则对上式做x方向上的傅氏变换后进入频率-波数域求解,可得下行波的解:

(11)

岩的数值模拟是基于垂直入射地震波的反射特征进行的,因此这里只需解出下行波即可。当地震波传播到黏弹性介质中时,Johnson[14]研究出如下关系:

(12)

式中:vP(ω)和Q(ω)分别为频变的地震P波相速度和品质因子。该式与公式(8)和公式(9)结合即可进行正演模拟。此外,由于相移正演时需要建立一个褶积模型形成初始波场,因此这里选用Ren等[15]提出的频变反射系数公式:

(13)

式中:vi和ρi(i=b,c)分别为含气储层和盖层的P波相速度和密度;α为地震波在黏弹性介质中的衰减系数。

(14)

2 数值模拟

为讨论不同含气量下砂岩储层地震波衰减特征的差异,设计了3种经典砂岩储层模型:深层固结良好的砂岩储层(模型1)、中等深度一般固结的砂岩储层(模型2)和浅层未固结的砂岩储层(模型3)。3种模型的岩石骨架与孔隙流体物性参数见表1[16],颗粒体积模量均为38GPa,密度均为2.65g/cm3。根据模型参数和斑块饱和模型频散关系公式,可得不同含气饱和度和渗透率下3种砂岩储层模型相速度和逆品质因子(1/Q)随频率变化的曲线,如图1和图2所示。

表1 3种砂岩模型的岩石骨架及流体物性参数

地震频带一般在数十Hz范围内,由图1a至图1c 可知,模型3中发生的地震波速度衰减和频散最强,其次是模型2,模型1最弱。含气饱和度对纵波相速度的影响较为明显,表现为含气饱和度越大,速度衰减越强,且在低频段(20Hz以内)频散严重。由图1d至图1f可知,增大渗透率能够对地震波的相速度造成类似的影响,即渗透率越大地震波的速度衰减越强烈,但相比含气饱和度,增大渗透率所造成的衰减相对较小,约数十m/s。观察图2中逆品质因子的频散曲线可知,随着频率的增加,3类砂岩储层模型中逆品质因子均表现为先增大后减小的趋势。随着含气饱和度的增大,逆品质因子的峰值对应频率也逐渐向频率增大的方向移动,这意味着地震波在高频部分的衰减会随着储层含气量增加更加强烈。此外,模型1逆品质因子峰值的大小随含气饱和度的增大而增大;模型2逆品质因子峰值的大小随含气饱和度的增大先增大后减小;模型3逆品质因子峰值的大小则随含气饱和度的增大而减小。随着渗透率的增大,逆品质因子峰值逐渐向高频方向移动,但总体来说峰值的大小并未发生明显变化。总的来说,在频率较高(20Hz以上)的情况下,含气饱和度越高,逆品质因子越高,地震波的衰减越强;在频率足够低(5Hz以内)的情况下,含气饱和度越高,逆品质因子越低,地震波的衰减越弱。

为进一步分析含气砂岩的地震响应特征,我们利用相移法频率-波数域波动方程正演进行数值模拟分析。所用地质模型的盖层和底层均为页岩(如图3所示),给定模型1中页岩的纵波速度为3100m/s,密度为2.4g/cm3;模型2中页岩纵波速度为2800m/s,密度为2.32g/cm3;模型3中页岩纵波速度为2500m/s,密度为2.2g/cm3。3种模型的夹层均为含气砂岩储层,其岩石骨架与流体的物性参数如表1所示。

图1 不同含气饱和度(a,b,c)和渗透率下(d,e,f)P波相速度频散曲线

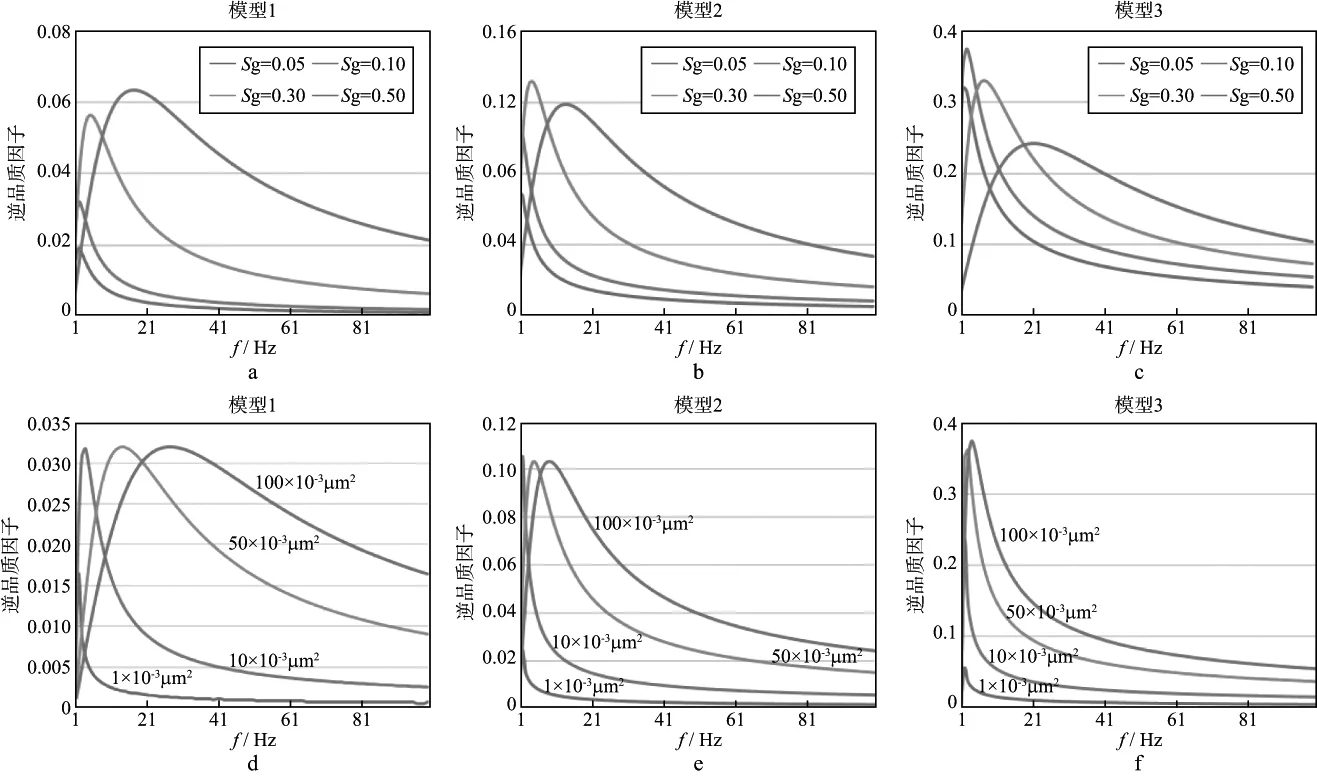
图2 不同含气饱和度(a,b,c)和渗透率下(d,e,f)逆品质因子频散曲线

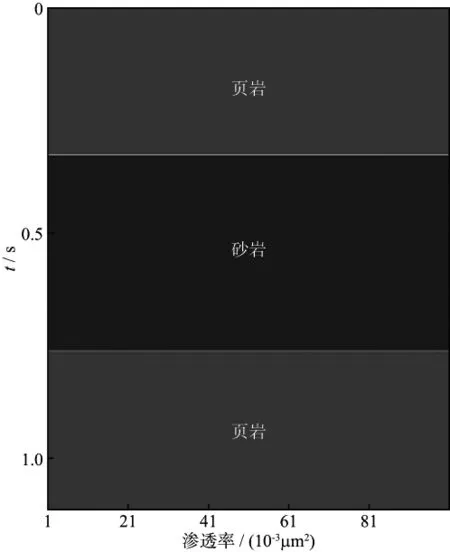
图3 正演模型

选用25Hz的雷克子波为震源,将各层介质的物性参数、速度和品质因子的频散关系代入方程(12)～方程(14),得到含气饱和度分别为0.1和0.5时的地震响应结果,如图4和图5所示。为了更全面地反映介质中渗透特性对地震响应的影响,我们将横坐标设定为渗透率,同时给出储层上、下界面反射波最大振幅的绝对值随渗透率变化的曲线,如图6和图7所示。

从图4可以看出,3种模型上界面反射波振幅受渗透率增大的影响均发生了较轻微的变化,下界面反射波振幅则随着渗透率的增大出现了不同程度的衰减,反映渗透率对储层地震波相速度的变化存在一定影响,并因此改变了储层内部波阻抗的大小。然而,渗透率只反映地层的岩石骨架特性,与所含流体无关。从图4c可知,储层下界面反射随渗透率的增大出现了较轻微的“下拉”现象,即反射波逐渐向时间增大的方向移动,这是由于渗透率的增大使P波相速度的衰减变强。然而这一现象并未在模型1和模型2的地震响应中有所体现。观察图6可知,随着渗透率的不断增大,3种含气砂岩模型的下界面反射波振幅均表现出不同程度的减小,模型1和模型2上界面反射波振幅出现轻微的衰减,而模型3则由于地震波速度的降低导致波阻抗差异变大,进而表现为反射波振幅的增大。但总体而言,由于含气量较少,反射波振幅变化的量级相对较小。

图4 含气饱和度为0.1时3类砂岩储层地震响应a 模型1; b 模型2; c 模型3

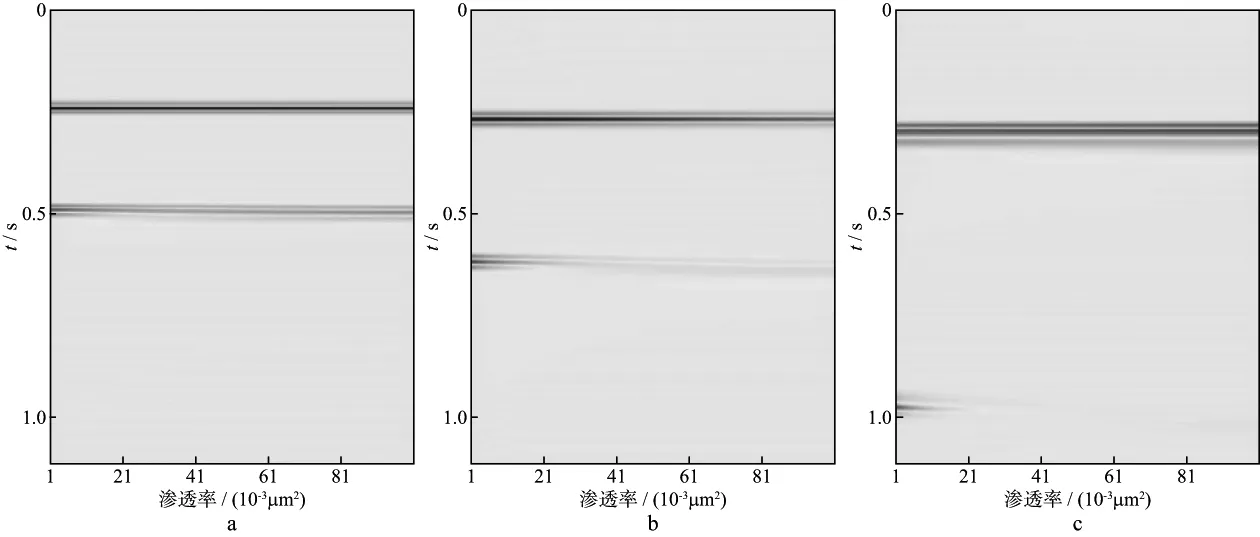
图5 含气饱和度为0.5时3类砂岩储层地震响应a 模型1; b 模型2; c 模型3

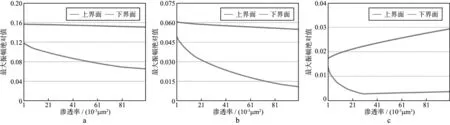
图6 含气饱和度为0.1时储层界面反射波振幅随渗透率的变化a 模型1; b 模型2; c 模型3

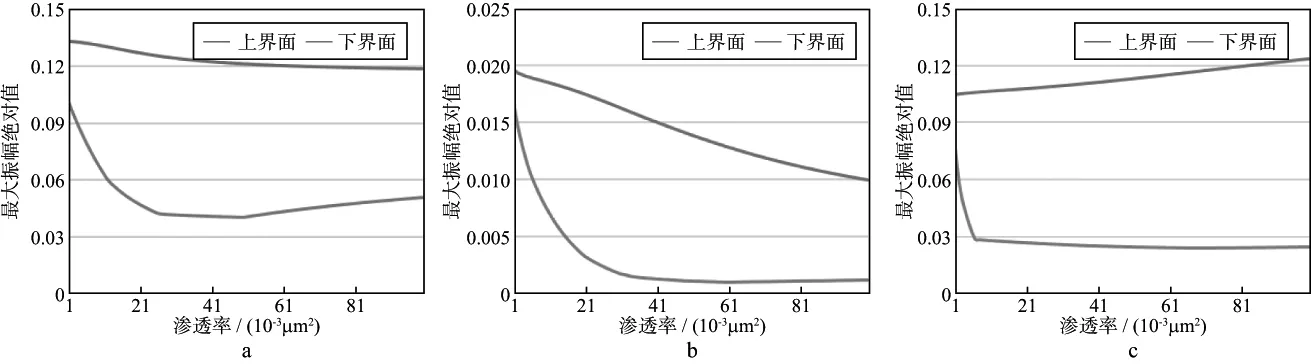
图7 含气饱和度为0.5时储层界面反射波振幅随渗透率的变化a 模型1; b 模型2; c 模型3

根据图5所示半饱和状态下的砂岩储层地震响应结果,3个模型的下界面反射波同相轴均发生了轻微的畸变,并随着渗透率的增大表现出一定的“下拉”现象,这说明储层含气量的增大也在一定程度上改变了介质中流体的流动性,进而造成了更强烈的衰减。对比图4和图5中3类砂岩储层模型下界面的反射特征不难发现,随着含气饱和度的增大,反射波在时间方向上均表现出十分明显的滞后,即反射波的时间延迟现象。其中未固结的模型3表现最为明显,延时约200ms,其次为模型2,模型1最不明显。这一现象说明含气饱和度的增大对P波相速度的衰减十分显著,并在地震剖面上表现为反射波时间上的延迟。同时,P波相速度的衰减也使含气层与底层页岩的波阻抗差异发生了变化,从而改变了反射波的振幅,这与图1分析的结果一致。图7分析结果与图6类似,但由于含气量增加,渗透率增大使介质中流体的流动能力增强,进而使地震波速度发生更为显著的衰减,最终导致反射波振幅发生更加明显的变化。

图8是3种模型在渗透率为10×10-3μm2、含气饱和度分别为0.1和0.5时的地震响应波形图。可以看出,含气饱和度由0.1增加到0.5后,3种模型的上、下界面反射波波形均发生了较明显的变化。其中,由于含气量的增加,地震P波相速度发生了十分明显的衰减,进而改变了砂岩储层内部的波阻抗,导致上、下界面反射波振幅均发生明显的变化。除此之外,各模型的下界面反射波均表现出较明显的时间延迟,可见含气量的增大对于砂岩储层中地震波速度的衰减有着巨大的影响。

渗透率的增大对P波相速度的影响相对较小,仅在低频段有数十m/s的差异,而在地震主频为20Hz以上的频段差异则相对较小[9],但仍能使下界面反射出现轻微的时间延迟(如图4c和图5c),因此渗透率的影响不可忽视。

图8 不同含气饱和度下储层地震响应波形a 模型1; b 模型2; c 模型3

图9为提取的3种模型含气层下界面反射波频谱示意图,可以看出,由于地震波传播到含气层时,速度发生了频散和衰减,含气饱和度的增大导致地震波在高频段衰减更剧烈,因此在频谱响应上表现为主频降低(即波峰向横轴上频率降低的方向移动)。同时,含气饱和度的增大导致含气层中地震波速度发生显著衰减,模型3中含气层与底层页岩的波阻抗差异变大,因此振幅增大,而模型1和模型2的波阻抗差异变小,因此振幅减小。这一现象也说明了含气饱和度的变化对于含气层中地震波的衰减和频散有着十分显著的影响。

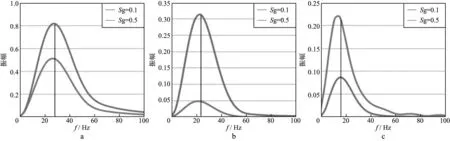
图9 不同含气饱和度下储层下界面反射波频谱a 模型1; b 模型2; c 模型3

3 结束语

地震波在未固结的砂岩储层中发生的衰减和速度频散最明显,中等固结的砂岩储层次之,固结良好的砂岩储层最弱。含气饱和度的变化对P波相速度的衰减影响较大,在地震频段可达数百m/s。在频率较高时,含气饱和度越高,逆品质因子越高,地震波的衰减越强;在频率足够低时,含气饱和度越高,逆品质因子越低,地震波的衰减越弱。渗透率越大,地震波的速度衰减越强烈,但相比含气饱和度,增大渗透率所造成的衰减相对较轻;同时,逆品质因子峰值随着含气饱和度或渗透率的增大逐渐向高频方向移动。

利用相移法波动方程正演进行数值模拟分析发现,随着渗透率的增加,砂岩储层中P波相速度发生了一定的衰减。同时,含气饱和度较低时,在未固结的砂岩储层中,下界面反射出现较微弱的时间延迟;而在半饱和状态下的含气砂岩中,3种砂岩储层中渗透率的增大均能形成反射波在时间上较轻微的延迟,说明含气量的增大改变了介质中流体的流动性,使地震波速度的衰减更加强烈。

不同含气饱和度下,3种砂岩储层下界面反射均表现出振幅变化和时间延迟现象,未固结的砂岩储层下界面反射时间延迟最明显,中等固结的砂岩储层次之,固结良好的砂岩储层最不明显。因此,基于White模型的理想砂岩储层中,含气饱和度的变化能显著地影响储层下界面反射波的动力学特征,而渗透率的影响则相对较小。此外,含气饱和度的增大也能造成地震波主频的降低。

需要指出的是,斑块饱和模型是基于中观尺度的流体流动衰减机制提出的,并假设介质中不同区域的物理性质有所差异,当地震波穿过斑块饱和介质时,会引起各区域流体之间的相互流动,因此造成能量的损失。本文采用的空间周期排列斑块饱和模型将各单元简化为规则的球体,符合常规较理想含气砂岩的物性特征,但并不适用于构造较复杂的砂体。中观尺度的能量衰减对岩石骨架和流体有较强的依赖性,且本文在正演过程中假设地震波在盖层和底层页岩传播时无能量损失,因此存在一定的局限性。故对于较复杂含气砂岩的地震响应特征还需要进行更深一步的探索和研究。

[1] BIOT M.Theory of propagation of elastic waves in a fluid saturated porous solid I:low frequency range[J].Acoustical Society of America Journal,1956,28(2):168-178

[2] BIOT M.Theory of propagation of elastic waves in a fluid saturated porous solid II:higher frequency range[J].Acoustical Society of America Journal,1956,28(2):179-191

[3] MAVKO G M,NUR A.Wave attenuation in partially saturated rocks[J].Geophysics,1979,44(2):161-178

[4] DVORKIN J,NOLENHOEKSEMA R C,NUR A.The squirt-flow mechanism:macroscopic description[J].Geophysics,1994,59(3):428-438

[5] WHITE J.Computed seismic speeds and attenuation in rocks with partial gas saturation[J].Geophysics,1975,40(2):224-232

[6] 邓继新,王尚旭,俞军.频散作用对储层砂岩速度实验结果的影响[J].石油物探,2005,44(4):334-338 DENG J X,WANG S X,YU J.Effect of dispersion on the experimental results of sandstone velocity in reservoirs[J].Geophysical Prospecting for Petroleum,2005,44(4):334-338

[7] 邓继新,王尚旭,俞军.孔隙流体分布对部分饱和储层砂岩速度实验结果的影响及理论分析[J].石油物探,2005,44(5):495-498 DENG J X,WANG S X,YU J.The effects of pore fluid distribution to the experimental velocity of partially saturated reservoir sandstones[J].Geophysical Prospecting for Petroleum,2005,44(5):495-498

[8] 李晓波,董良国.斑块饱和介质的粘弹特性表征与地震波模拟[J].石油物探,2014,53(3):272-279 LI X B,DONG L G.Viscoelastic representation of patchy saturation media and its seismic wave simulation[J].Geophysical Prospecting for Petroleum,2014,53(3):272-279

[9] RUBINO J G.Permeability effects on the seismic response of gas reservoirs[J].Geophysical Journal International,2012,189(1):448-468

[10] 王峣钧,陈双全,王磊,等.基于斑块饱和模型利用地震波频散特征分析含气饱和度[J].石油地球物理勘探,2014,49(4):715-722 WANG Y J,CHEN S Q,WANG L,et al.Gas saturation analysis with seismic dispersion attribute based on patchy-saturation model[J].Oil Geophysical Prospecting,2014,49(4):715-722

[11] 陈程,文晓涛,郝亚炬,等.基于White模型的砂岩储层渗透率特性分析[J].石油地球物理勘探,2015,50(4):723-729 CHEN C,WEN X T,HAO Y J,et al.Sandstone reservoir permeability characteristics analysis based on White model[J].Oil Geophysical Prospecting,2015,50(4):723-729

[12] GAZDAG J.Wave equation migration with the phase-shift method[J].Geophysics,1978,43(7):1342-1351

[13] HILL R.Elastic properties of reinforced solids:some theoretical principles[J].Journal of Mechanics & Physics of Solids,1963,11(5):357-372

[14] JOHNSON D L.Theory of frequency dependent acoustics in patchy-saturated porous media[J].Journal of the Acoustical Society of America,2001,110(2):682-694

[15] REN H,GOLOSHUBIN G,HILTERMAN F.Poroelastic analysis of amplitude-versus-frequency variations[J].Geophysics,2009,74(6):N41-N48

[16] REN H,GOLOSHUBIN G,HILTERMAN F.Poroelastic analysis of permeability effects in thinly layered porous media[J].Geophysics,2009,74(6):N49-N54

(编辑：戴春秋)

Analysis of seismic response characteristics from vertical incident insandstone gas reservoir based on the White model

LI Shikai1,2,WEN Xiaotao1,2,RUAN Yunqi1,3,LI Tian1,2,ZHANG Rui1,2,ZHANG Jinming1,2

(1.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation(ChengduUniversityofTechnology),Chengdu610059,China;2.CollegeofGeophysics,ChengduUniversityofTechnology,Chengdu610059,China;3.CollegeofEnergy,ChengduUniversityofTechnology,Chengdu610059,China)

Based on the White’s sphere patchy saturated model and dynamic bulk modulus theory,in this paper we analysis the effect of gas saturation and permeability on seismic phase velocity and inverse quality factor in different sandstone reservoirs,including well consolidated sandstone,medium consolidated sandstone and unconsolidated sandstone.Great attenuation can be observed on phase velocity of P-wave due to the increasing of gas saturation increasing,which can be as high as hundreds of meters per second in seismic frequency band and slightly attenuation can be brought by increasing permeability.And the inverse quality factor is higher when the gas saturation and frequency are both high,which leads to greater attenuation of seismic energy.The simulation results of seismic response for 3 types of sandstome reservoirs based on the phase-shift wave equation shows by phase-shift that “time delay” on the reflection from lower interface can be observed by increasing gas saturation,especially in the unconsolidated and consolidated sandstone reservoir.Furthermore,the main frequency of seismic energy will decline when gas saturation is increased.If containing gas is at a high saturation state,the flow of fluid medium will be enhanced,resulting in greater attenuation of seismic energy by increasing permeability.

patchy saturated model,gas sandstone,gas saturation,wave equation simulation,permeability,time delay

2016-05-23;改回日期：2016-09-19。

李世凯(1991—),男,硕士在读,主要从事波动方程正演偏移及储层预测研究。

国家自然科学基金石油化工联合基金(U1562111)和中国石油化工股份有限公司地球物理重点实验室开放研究基金(33550006-15-FW2099-0029)共同资助。

P631

A

1000-1441(2017)02-0232-08

10.3969/j.issn.1000-1441.2017.02.010

This research is financially supported by the National Natural Science Foundation of China (Grant No.U1562111) and SINOPEC Key Laboratory of Geophysics Open Foundation(Grant No.33550006-15-FW2099-0029).

李世凯,文晓涛,阮韵淇,等.基于White模型的含气砂岩垂直入射地震响应特征分析[J].石油物探,2017,56(2):-239

LI Shikai,WEN Xiaotao,RUAN Yunqi,et al.Analysis of seismic response characteristics from vertical incident in sandstone gas reservoir based on the White model[J].Geophysical Prospecting for Petroleum,2017,56(2):-239