基于LQI权重和改进粒子群算法的室内定位方法*

尚俊娜，盛 林，程 涛，施浒立，岳克强

(1.杭州电子科技大学通信工程学院，杭州310018;2.中国科学院国家天文台，北京100012; 3.杭州电子科技大学电子信息学院，杭州310018)

基于LQI权重和改进粒子群算法的室内定位方法*

尚俊娜1*，盛 林1，程 涛1，施浒立2，岳克强3

(1.杭州电子科技大学通信工程学院，杭州310018;2.中国科学院国家天文台，北京100012; 3.杭州电子科技大学电子信息学院，杭州310018)

为解决无线传感网络节点在室内定位中由非视距和多径传输等因素导致定位误差较大的问题，提出了基于三角函数的粒子群算法。针对RSSI波动性引起的测距误差，利用LQI和RSSI值之间的关系对RSSI值进行优化，提出了基于LQI权重的RSSI测距算法。改进的粒子群算法相比较于标准粒子群算法优化了权重模型和速度更新策略，避免陷入局部最优值情况。在对算法进行仿真实验后，进一步将其运用到Zigbee平台的定位实验，通过实测实验证明该算法在测试环境下平均定位误差在0.5 m以内，相比于LSE和标准PSO算法，获得较好的定位效果。

室内定位;衰减模型;粒子群算法;RSSI;LQI

无线传感网络WSN(Wireless Senor Network)作为新的信息获取和处理技术，在环境监测、火灾预警、医疗卫生、物件跟踪等领域得到应用［1］。在无线传感网络应用中，位置信息对传感网络的监测监控活动至关重要，缺少有效位置的监测监控信息是无意义的，因此研究获取节点的位置信息对无线传感网络的广泛应用具有决定性作用。

无线传感网络的室内定位技术已成为国内外研究的热点，各种算法层出不穷，如刘政等人引入改进RSSI测距，降低测距误差，并引用PSO算法搜索MDS坐标变化，寻找最优位置估计［2］。闫驰等人将PSO算法作为BP网络的学习算法，通过粒子群算法在搜索寻优方面的优势，缩短BP神经网络的学习时间，提高定位速度［3］。王千等人研究了实测距离与模型预测距离关系，建立锚节点概率环形区间，提出概率区间交叠定位算法，并以多边界质心算法为辅，组成混合定位［4］。室内定位技术中利用无线电信号实施定位的方案得到较多的研究，该方案根据定位过程中是否需要测量实际节点间的距离，可分为测距和非测距两大类，而基于测距方法的由于实施较为简单、精度较高而得到较为广泛的应用。典型的测距技术有到达角AOA(Angle of Arrival)［5］、到达时间TOA(Time of Arrival)、到达时间差 TDOA(Time Delay of Arrival)［6］和接收信号强度值 RSSI(Received Signal Strength Indicator)［7］等。基于RSSI的测距技术更适合于对硬件的要求低、功耗低的无线传感网络，并提供了最便捷的测距方法，在无线传感器网络定位技术中较常采用。其接收和计算无线信号强度是商用无线通信芯片的基本功能，通过分析节点间的接收信号强度推断出距离，无需额外的硬件开销，是现有无线传感网中较好的测距技术。

本文在研究当前的RSSI测距技术的基础上，通过测距实验分析了与信号传播有关的RSSI值和链路质量指示LQI(link quality indicator)之间的区别和联系，从而提出了一种基于LQI权重的RSSI距离计算方法，在完成测距后使用改进的粒子群算法实现无线节点的定位，并通过实验验证所提出方法的性能，结果表明在不增加通信开销和硬件成本的情况下实现定位精度的提高。

1 基于LQI权重的RSSI距离估计算法

1.1 RSSI测距原理与模型

空旷的环境下，无线信号强度与传播距离存在函数关系，考虑在自由空间中(无障碍物)，发射天线的功率为PT，传递到接收天线的功率为PR，锚节点和盲节点之间距离为d，电磁波频率f，波长λ，环境衰减系数n。假设发射天线是全方位的，没有天线损耗。则电磁波的传播方程［8］表示为:

实际上天线都是有损耗的并且存在方向性，设发射天线的增益为GT，接收天线的增益为GR，则式(1)变为:

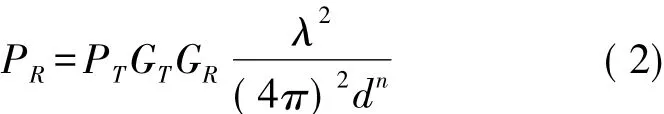
由于接受信号强度RSSI使用dBm表示，需要将式(2)左右两边取对数，变为:

最终表示为Shadowing模型公式［9］:

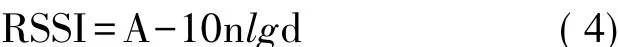
根据式(4)可知，得到锚节点和盲节点之间的接收信号强度值，以及环境衰减系数即可计算出信号传输距离。A通常取1 m处测得的RSSI值。

1.2 基于LQI权重的RSSI测距算法

无线传感网络在实际应用环境中，由于室内的电磁波传播条件和状态均为多变，导致发射信号经过多径传播到达接收端，从而改变信号的包络和相位，这将使得式(4)计算出的距离出现较大误差。这种多径现象来源于楼层遮挡、建筑物类型和人为因素包括天线放置、建筑物中人的数量和日常活动，从而造成信号传播距离的精度较差等情况，给RSSI测距带来很大的困难。

为验证RSSI理论模型的测距效果，随机选择一对CC2530节点进行测试。两节点分别设置为一发一收状态，在不同距离下，读取数据包中的RSSI值，结果如图1所示。图中对比了实测RSSI值与距离值的关系和由Shadowing模型得到的RSSI值与距离在理想状态下的关系。由图可知，RSSI测量值与理论值存在一定的差异性，而且随着距离的增加，误差得到放大。直接使用测量的RSSI值计算距离会造成很大的误差，因此在WSN定位中，有必要对RSSI测距的模型进行改进和提高。

图1 RSSI与距离变化关系图

LQI值是链路质量的直接评估量，表示接收数据帧的能量与质量，其大小基于信号强度以及检测到的信噪比SNR(Signal Noise Ratio)，由介质访问层计算得到并提供给上一层，与正确接收到数据帧的概率有关。为研究RSSI值和LQI值之间的区别与联系，本文选用德州仪器公司(TI)开发的用于2.4 GHz通信，符合IEEE802.15.4标准协议的CC2530模块进行测试。

CC2530有一个内置的接收信号强度指示器，RSSI值和LQI值可以从寄存器读出，或自动附加到接收到的帧，其帧格式主体如表1所示。

表1 Zigbee数据帧格式

数据帧主要包含的是源地址(srcAddr)、目的地址(macDstAddr)、链路质量指示(LQI)、接收信号强度指示(RSSI)、消息包(MSG)等，其中LQI值为无符号的整形数据，而RSSI为有符号的整形数据。

图2和图3分别为接收节点放置在3 m和6 m处时，静态测得的RSSI值和LQI值的变化。从图中可以看出LQI的水平决定了RSSI值的优劣性，相同位置测得的LQI值较高时，所得到的RSSI值较稳定，如果LQI值存在波动时，RSSI值不稳定。尤其是LQI值较小时，信号收到的噪声干扰大，此时RSSI值不可靠。

图2 距离3 m时LQI与RSSI关系图

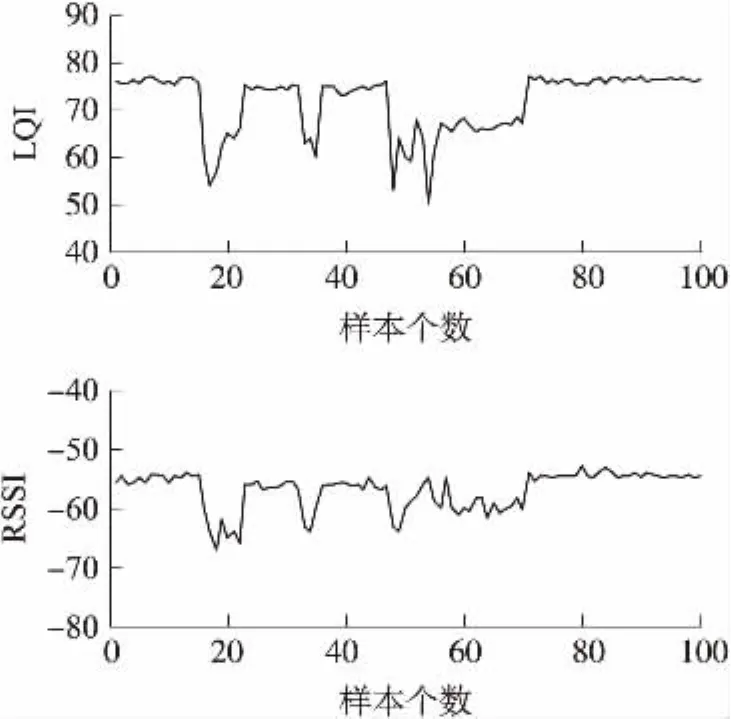
图3 距离6 m时LQI与RSSI关系图

根据以上测试结果，本文提出基于LQI权重的RSSI测距算法，如式(5)所示:

式中:RSSIi为相同距离时测得的多个RSSI值，LQIi为相同距离下RSSIi所对应的LQI值，αi为相应的匹配系数，N为总的样本个数。该模型的基本思想是减小不可靠的RSSI值带来的测距误差。基于较大的LQI值时，链路质量较好，各种噪声和干扰较小，对应的RSSI值较准确，而较小的LQI值对应的RSSI值就存在波动性。故在设置的系数方面，准确的RSSI值分配的系数较大，即占的比重大。而较小的LQI值对应的RSSI值存在波动性，部分是可用的，分配较小的权重。这样所得到的RSSI值计算的距离值，相比于单一的RSSI值计算将更加精确，从而获得更好的定位精度。

2 改进的粒子群定位算法

2.1 标准粒子群算法原理

粒子群优化算法PSO(Particle Swarm Optimization)是Eberhart R C和Kennedy J于1995年提出的一种新的进化算法，算法规则简单，较为容易实现，并且精度高，收敛速度快。该算法是从随机解出发，通过迭代的方法寻求最优解，然后通过适应度函数来评判解的优劣，它通过使用当前搜索到的最优值来寻找全局最优。粒子群算法的模型是速度和位置的更新，该算法原理为:一群具有随机初始速度和位置的粒子，跟踪局部最优值(pbest)和全局最优值(gbest)不断更新，通过迭代寻找最优解［10］。设在n维空间中有N个粒子组成的粒子群，粒子速度为vi=(v1，v2，v3，…，vN)，粒子位置为pi=(p1，p2，p3，…，pN)，下一代粒子的速度和位置更新公式如下所示:

式中:i为粒子群中第i个粒子，t为当前迭代次数，ω为惯性权重，c1和c2表示学习因子，r1和r2表示在区间(0，1)上均匀分布的随机数，且相互独立。

标准的粒子群算法在寻找最优解的过程中，若检测到其中任意粒子为最优位置时，其他粒子则迅速调整速度向其靠拢。这使得粒子容易陷入局部极小值，而无法跳出一定范围继续搜索全局最优解。

2.2 改进的粒子群算法

本文提出的粒子群算法主要在于加入三角函数对惯性权重值和粒子速度更新策略两个方面进行优化，提高定位结果的准确性。

惯性权重ω是粒子群算法当中特别重要的参数之一，它决定了当前的速度和位置参数对下次迭代的速度和位置参数的影响程度。研究表明，较大的惯性权重取值可增强全局搜索能力，粒子收敛速度快，缺点是解的准确度下降;反之，提高局部搜索能力，准确度有所提高，但收敛速度降低且容易陷入“早熟”现象［11］。合理的ω取值可以平衡两者的优缺点，提高算法寻优的稳定性。

研究表明，惯性权重较好的选择是递减策略［12］，因此本文提出一种基于sin函数的惯性权重递减策略。改进的惯性权重是非线性变化，所提出的惯性权重公式为:

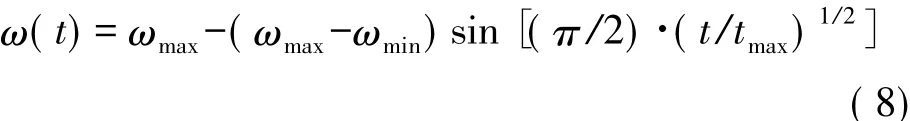
式中:ωmax代表最大的惯性权重，ωmin代表最小的惯性权重，t为当前的迭代次数，tmax则为最大迭代次数。图4给出了ωmax=0.9，ωmin=0.2时惯性权重的递减曲线。

图4 三角函数模型惯性权重递减曲线

由改进的惯性权重递减曲线可以看出，在迭代初期ω取值较大，加快向全局最优解的聚集速度，再通过加速惯性权重的递减速度来让算法较快进入局部搜索;迭代后期减缓递减速度，从而对最优解进行更加精细的搜索，获得高精度的解。从曲线的变化趋势可以看出，整个曲线呈现凹函数递减，通过此种方式调节惯性权重，可以获得较好的效果。

在标准的PSO算法中，粒子的速度更新同样受制于前一代局部最佳位置pbesti和全局最佳位置gbesti。为了降低每次更新后粒子位置的剧烈变化给下一代粒子位置带来波动性，本文加入两个最佳位置与每个粒子位置的差值信息进行约束，改进后的速度更新公式为:

改进后的速度更新策略与原本的相比，效果如图5所示。

图5 速度更新对比图

同样使用三角函数，可防止因粒子位置更新的较大差异而对速度更新造成跳变，这得益于三角函数的值域为［－1，1］。位置信息差和三角函数的应用实现对粒子速度的控制，让粒子的寻优过程变得平缓，适当降低收敛速度，防止粒子陷入局部最优解。

节点定位的具体流程如下:①在目标区域中部署一定数量的锚节点，启动Zigbee网络。各锚节点以广播的方式向周围播发消息，内容包括节点的ID和坐标等有用信息。②盲节点接收消息，解析数据包的内容，并提取每一次的RSSI值和LQI值。判断相应锚节点收集的数据包是否均满足一定数量，若满足则使用本文距离估计算法计算盲节点到锚节点的距离值。③初始化改进的粒子群算法，包括粒子数量、位置和速度等，将测得的各个距离值代入适应度函数并计算出定位结果。

3 实验和分析

3.1 基于LQI权重的RSSI测距实验

为验证算法，采用CC2530模块搭建WSN定位实验平台。首先对基于LQI权重的RSSI测距算法验证。在空旷环境下，随机选择1对节点进行测距实验。根据信号传播的两径模型，天线距离地面越近，信号衰落越快，当频率为2.4 GHz时，天线高度至少达到0.6 m。故在实验中使得节点距离地面1 m左右，如图6所示，发射功率0 dBm，天线增益3 dB，盲节点与锚节点每隔0.25 m测量一次，最远测到10 m处。

每个距离处测量50组数据，获取RSSI和LQI值后代入改进后的 LQI-RSSI模型计算出相应的RSSI值，然后按照式(4)计算出距离。实验将基于LQI权重的RSSI测距算法、统计均值测距算法以及高斯滤波测距算法［13］作比较，3种方法的测距误差曲线如图7所示。

图6 RSSI测距实验

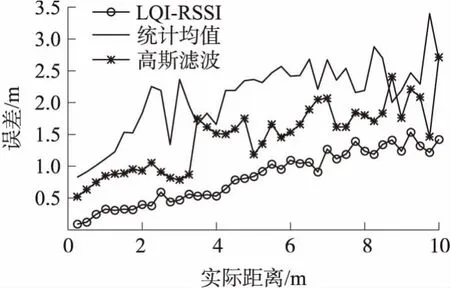
图7 3种算法结果误差对比

表2展示了整数距离处的测距结果以及所有距离处测距误差的均值和标准差。由实验结果可知，本文提出的算法能够有效解决RSSI的波动性，提高测距精度。

表2 测距结果

3.2 定位仿真实验

为验证本文所提改进算法在室内定位中性能的提升，分别在仿真环境和实际环境中进行试验分析。由于在WSN定位中，计算的距离均存在误差，因此定位问题的本质是使得产生定位的误差最小化。在WSN定位中，由于使用了k个锚节点进行定位实验，因此本文采用多个锚节点的测距误差和的均值作为最终的适应度函数:

式中:(x，y)为盲节点准确坐标，(xi，yi)为第i个锚节点坐标，di为第i个锚节点坐标与盲节点的计算距离，实验结果以平均定位误差作为衡量算法定位精度的评价标准，即:

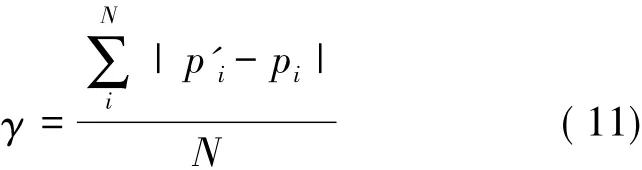
式中:N为未知节点的个数，p'ip为盲节点i的真实位置，pi为盲节点i的计算位置。定位算法的参数设置如表3所示。

表3 定位算法参数设置

本文针对不同锚节点数量和测距误差对未知节点定位的影响分别做了仿真实验。在25 m×25 m的正方形区域随机设置传感器节点，其中锚节点20个，盲节点10个，节点的通信半径设为10 m。为进一步验证改进的粒子群算法性能，将结果和标准的粒子群算法以及最小二乘估计(LSE)算法［14］进行对比，结果如图8、图9所示。

图8 锚节点个数对定位精度的影响

图9 测距误差对定位精度的影响

图8为在锚节点数量增加时，3种算法平均定位误差比较。由图8可知，平均定位误差随着锚节点数量的增加而逐渐下降，并且改进后的算法收敛速度块。当节点数量大于12个以上时，两种粒子群算法的平均定位误差比最小二乘估计算法下降速度慢，表明锚节点在增加到一定数量后，对定位误差的影响逐渐减小。

测距误差对于定位结果的影响很大，图9为测距误差在不同百分比情况下的3种算法平均定位误差比较。在相同条件下，改进的粒子群算法比其他两种算法定位误差小，获得较好的效果。

3.3 定位验证实验

实际环境中的定位实验分别使用4个锚节点(T1～T4)和12个锚节点(T1～T12)分布在边长为6 m的正方形边界上，将该正方形区域均分成九宫格，对每个格子中间点进行定位测试，如图10所示。

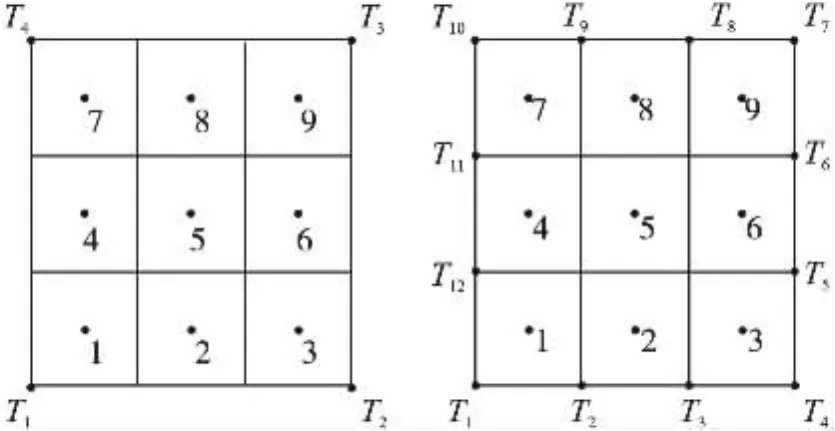
图10 定位实验点布置图

实验结果同样与标准的粒子群算法以及最小二乘估计算法进行对比，定位误差如图11和图12所示。

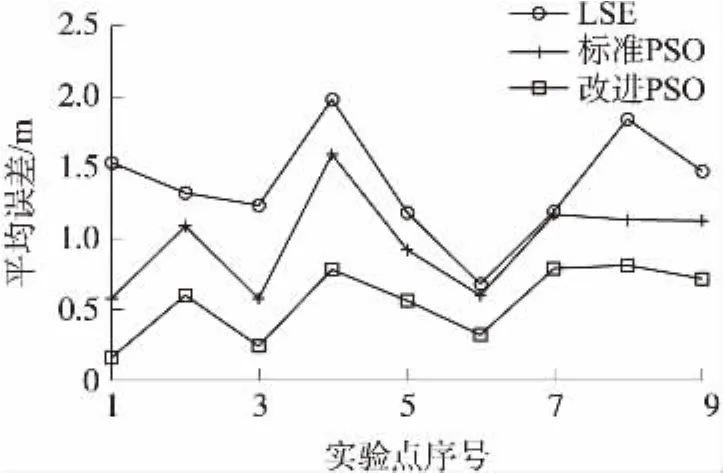
图11 锚节点为4时平均误差对比图

图12 锚节点为12时平均误差对比图

图12清楚的展示3种算法的平均误差，横坐标是9个测试的序号，纵坐标是定位的平均误差。定位结果的误差的均方值如表4所示，明显的粒子群算法要比最小二乘估计算法计算结果较好，而本文提出的改进算法要优于标准的粒子群算法。

表4 定位实验误差均方值

4 结论

基于RSSI的定位技术是无线传感器网络定位中的一个常见方法，并且节点的定位本质上是一种优化问题。本文针对WSN定位的影响因素，采用两种优化策略实现对定位精度的提高:其一是通过了解无线信号的RSSI传播规律，分析影响RSSI值变化的因素，提出基于LQI权重的RSSI测距模型;其二是研究了粒子群算法的优缺点，针对标准PSO算法易陷入局部最优问题，提出基于三角函数的PSO算法。本文所提的改进算法在不增加硬件设施要求情况下有效提高节点的定位精度，因此对于节点的WSN定位来说，是一种较好方案。

［1］ Goldoni E，Savioli A，Risi M，et al.Experimental Analysis of RSSIBased Indoor Localization with IEEE 802.15.4［J］.Wireless Conference(EW)，2010 European，Lucca，2010:71－77.

［2］ 刘政.基于粒子群优化的多维标度节点定位算法［J］.传感技术学报，2015，28(8):1228－1232.

［3］ 闫驰.基于PSO-BP神经网络的无线传感器网络定位算法［J］.电子科技，2016，29(4):56－58，62.

［4］ 王千，金光，钮俊，等.一种基于RSSI的混合定位算法［J］.传感技术学报，2015，28(12):1823－1829.

［5］ Tomic S，Beko M，Dinis R.Distributed RSS-AoA Based Localization with Unknown Transmit Powers［J］.IEEE Wireless Communications Letters，2016，5(4):392－395.

［6］ 王千，金光，钮俊，等.一种基于RSSI的混合定位算法［J］.传感技术学报，2015，(12):1823－1829.

［7］ Janicka J，Rapinski J.Application of RSSI Based Navigation in Indoor Positioning［J］.2016 Baltic Geodetic Congress(BGC Geomatics)，Gdansk，Poland，2016:45－50.

［9］ 郑学理，付敬奇.基于PDR和RSSI的室内定位算法研究［J］.仪器仪表学报，2015，36(5):1177－1185.

［10］赵雁航，钱志鸿，尚小航，等.基于跳距修正粒子群优化的WSN定位算法［J］.通信学报，2013，(9):107－116.

［11］刁绫，石为人，冉启可，等.基于粒子群优化的DV-Distance改进算法［J］.仪器仪表学报，2014，(z2):12－19.

［12］Elons A S，Magdi D A，Elgendy M Y.A Proposed Model for Predicting the Drilling Path Based on Hybrid Pso-Bp Neural Network［J］.2016 SAI Computing Conference(SAI)，London，United Kingdom，2016:148－155.

［13］温佩芝，苏亭婷，李丽芳，等.基于粒子群的射频识别定位算法［J］.计算机工程与科学，2014，36(5):917－922.

［14］徐琨，刘宏立，马子骥，等.一种针对未知发射功率的室内定位优化算法［J］.传感技术学报，2016，29(6):915－919.

尚俊娜(1979－)，女，博士，杭州电子科技大学通信工程学院副教授，主要研究方向卫星导航通信，shangjn@hdu.edu.cn;

盛 林(1991－)，男，汉族，安徽省安庆市人，杭州电子科技大学通信工程学院硕士研究生，主要研究方向为无线传感器网络定位，13735875735@163.com。

The Indoor Localization Based on LQI weight and Improved Particle Swarm Optimization Algorithm*

SHANG Junna1*，SHENG Lin1，CHENG Tao1，SHI Huli2，YUE Keqiang3
(1.College of Telecommunication Engineering，Hangzhou Dianzi University，Hangzhou 310018，China; 2.Chinese Academy of Sciences，National Astronomical Observatories，Beijing 100012，China; 3.College of Electronic Information，Hangzhou Dianzi University，Hangzhou 310018，China)

In order to solve the positioning error caused by non line-of-sight and multipath transmission in indoor location of wireless sensor networks，particle swarm optimization algorithm based on trigonometric is proposed.In view of the range error caused by RSSI fluctuation，this paper uses relationship between LQI and RSSI to optimize the RSSI value，and puts forward RSSI ranging algorithm based on LQI weight.Compared to the standard particle swarm optimization algorithm，the improved algorithm improves the weight model and the velocity update strategy，which avoids the local optimal value.After the simulation experiment，it is further applied to the Zigbee platform positioning experiment.The results show that the proposed algorithm has higher accuracy compared to the traditional ranging and positioning algorithm，which average localization error is less than 0.5m.

indoor localization;attenuation model;particle swarm optimization algorithm;RSSI;LQI

TP393

A

1004－1699(2017)02－0284－07

C:7230;6150P

10.3969/j.issn.1004－1699.2017.02.020

项目来源:浙江省自然科学基金青年基金项目(LQ13F010010);浙江省重点科技创新团队“固态存储和数据安全关键技术创新团队”项目(2013TD03);浙江省“电子科学与技术”重中之重学科开放基金项目(GK13020320003/004)

2016－07－27 修改日期:2016－10－03