基于光纤光栅的液体粘度测量方法的研究*
2017-04-13赵美蓉黄银国
陈 曦,赵美蓉,黄银国
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
基于光纤光栅的液体粘度测量方法的研究*
陈 曦,赵美蓉*,黄银国
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
针对液体粘度在线测量问题,提出了一种基于光纤光栅的液体粘度测量方法,即通过检测光纤光栅中心波长的变化量测得液体自身的粘度值。这种依靠液体自身流动得到液体粘度的方法是对粘度在线测量问题的一种新的探索和突破。在液体流动过程中,利用光纤光栅感知阻流元件表面粘滞力引起的悬臂梁的应力变化,对解调出的波长变化量经过计算得到应力变化的大小,从而得到相对应的粘度值。通过实验研究,对于粘度标准液进行光纤光栅的标定,建立了中心波长变化量与粘度的数学模型。最终,进行验证性实验,测量一组液体的粘度值,并与标准粘度计测得的结果进行比对,证明了实验方法的可行性。
液体粘度在线测量;光纤光栅;波长变化量;阻流元件
粘度是液体的重要物理性质,它反映液体流动行为的特征。提高粘度测量的精度可以降低生产过程中的成本,创造更大的经济价值和社会价值[1]。传统的粘度测量方法主要包括毛细管法[2]、落球法、旋转法[3]、振动法等。这些测量方法大多适于实验室离线检测,从取样至检测粘度有时间滞后,所测粘度不具有实时性,无法满足工业现场的测量要求。液体粘度的实时在线测量,不仅解决了取样问题,而且实时输出粘度值,提高了生产效率和产品质量。目前,国内不少学者提出了一些新的粘度在线测量方法。超声横波粘度测量方法适合于高粘度液体的实时在线测量,具有非接触无损检测的特点[2]。沉降式粘度测量方法是利用压差传感器软测量粘度的一种在线检测方法,适合于混合悬浮液的粘度测量。基于电磁感应的液体粘度测量方法利用电机使旋转体在液体中产生力矩并实时监测力矩与粘滞系数的关系也能实现液体粘度的在线测量[3]。振动式在线粘度计通过检测由于粘度阻力变化而损失的能量得到粘度值[4]。本课题组与中海油合作研制的电磁活塞式粘度计,已于2012年投入使用,可以对原油粘度进行准确测量[5]。但是这些测量方法由于安装成本过高,操作复杂,不具有普遍性。
本文基于牛顿粘性定律对流体粘度的在线测量系统进行了探索和研究,在满足实验结果的基础上,考虑可行性和成本因素,采用了光纤光栅技术,由于光纤光栅体积小、重量轻、耐腐蚀且无需电源驱动[6],并且能够通过分布式阵列进行多点测量,于是探索了利用液体自身流动的在线粘度测量方法。具有一定的创新性和突破性。
1 测量原理
牛顿粘性定律给出了粘度与内摩擦力的定量关系,通过构造一种简单的剪切流动,使它只有一个剪切力和剪切变率,然后分别测定剪切力和剪应变率来得到粘度。

式中:du/dr为速度梯度;η为粘度;S为流层间的接触面积;F为粘性力。
本文的测量原理基于细管型粘度测量计的基础上进行了改进,细管型粘度测量的基本原理如图1所示。
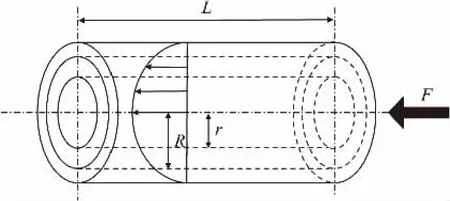
图1 流体受力示意图
当细管长度为L,内半径为R,细管两端的压强差为P,液体在外力F的作用下做匀速流动。考虑到力的平衡,在稳定流的条件下,外力与粘性力平衡,由此可得到平衡方程[7]:
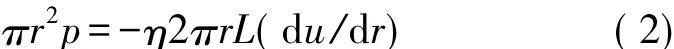
如图2所示,剪切速率du/dr随着流速半径r 的增大而减小,通过泊肃叶定律得到流量与粘度系数的关系如下

图2 流速分布示意图
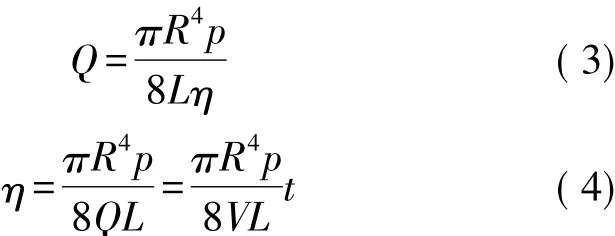
依据细管型粘度测量计的原理,选取在管道中添加阻流元件的方式进行测量。当介质流过时,对阻流元件产生的力F可概括为由两部分组成:流体动压力F1和粘滞摩擦力F[8]2。

参考流体力学,当流量较大时,

式中:β是阻力系数,与液体本身的性质有关,ρ为流体密度,V为平均流速,A为阻流元件的横截面积。
此时流体动压力F1起主导作用,它与流体流速的平方、流体密度及阻流元件的迎流面的面积成正比,当流速或流量变小时,流体的动能随之减小,流体对阻流元件的动压力也相应减小,这时管型阻流元件所受的力主要来自于流体与阻流元件之间的粘性摩擦,即粘滞摩擦力。
所以在低流量的条件下,当阻流元件为细管型时,迎流面积很小,流体动压力接近于0,粘滞力起主要作用。当圆管中流体处于不同流态时的管流有效剪切速率计算公式可以统一写成以下形式[9]:
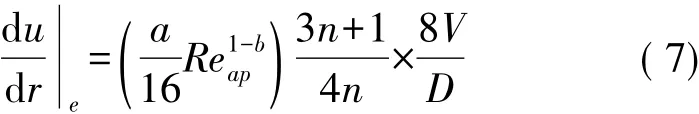
式中:V为流速,Re为雷诺数,D为管道直径。层流状态下,牛顿流体a=16,b=1,n=1;非牛顿流体a= 16,b=1,n为非牛顿性的度量,n偏离1越远,非牛顿性越明显[10]。根据式(1)和式(7)以计算出粘滞力与平均流速和粘度系数有关,如式(8)所示。

式中:k(n)是一个与n相关的特性系数,一般与液体自身特性有关,η为粘度系数,V为平均流速。
当用于固定光纤光栅的柔性悬臂梁置于介质流体中时,其所受到的冲击压力F3,对于粘度测量的结果也有一定影响,根据动量定理,F3与流量大小以及悬臂梁在液体中的面积有关,当在小于0.57 m/s的流速下,经过COMSOL Multiphysics 5.2仿真,在悬臂梁只受F3的情况下,所受的冲击压力为0 N,所以可以忽略不计。在这样的条件下,悬臂梁形变所受到的力只有流体动压力和粘滞摩擦力[11]。现在考虑半径为R,表面积为2πRL的液体圆筒上力的平衡。在稳定流的条件下,外力与粘性力平衡。如图3所示。
图3 平衡示意图
传感用裸光栅的安装十分简单,和安装传统的应变片差不多,同时,传感用光纤光栅具有尺寸小,重量轻的特点,在使用过程中对于装置精度的影响极小,能够实现对于应力应变的绝对测量,性价比高,在测量过程中不受电磁干扰,适用于需要精密定位的场合[12]。当光纤光栅处在一个温度场和压力场都保持不变环境之中,FBG仅仅受到轴向应力的作用时,以假设栅距变化量与它所受到应变方向是一致的[13],即:

则可以写为:
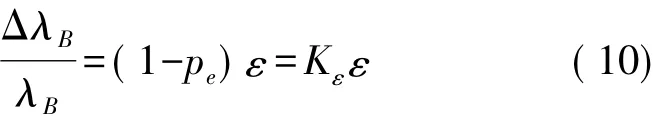
式中:λB为FBG的布拉格波长,Λ为光纤光栅的光栅周期,ε为其所受到的轴向应变,pe为有效弹光系数,Kε为FBG的应变灵敏度系数。
参照粘滞力式(8)得到:
式中:Q为流量;K为应变灵敏系数;A为细管型阻流元件横截面积;Λ为光纤光栅原始中心波长;
令

得到:

经过理论分析,中心波长的变化量越大,粘度值越大。
2 系统实现

图4 系统结构图
整个测量装置的结构图如图4所示,其中悬臂梁结构用于固定光纤光栅,选取灵敏性较高、弹性滞后小、温度系数小、耐腐蚀性强的紫铜材质,用于检测应力变化[14]。悬臂梁上设有4个螺孔的固定端,保证悬臂梁被完全固定,其中最薄部分的厚度为0.2 mm。将裸光栅(两端FAC接头)用氰基丙烯酸酯快干胶水粘贴在距离悬臂梁底部75 mm的位置。另外,外管道内径8 mm,外径为10 mm。阻流元件直径和流体管道内径之比的合理取值为q=0.6,阻流元件直径为4.8 mm,长度为30 mm。
当液体通过阻流元件时,阻流元件受到粘滞力的作用使悬臂梁产生形变,从而黏贴在悬臂梁上的光纤光栅由于形变而使中心波长发生变化。其变化经过Smart Fibers 3100-3011-A动态光纤光栅解调仪解调,输出波长变化信号,最终获得实验数据[6]。
为了固定光纤光栅,必须设计应变效果明显的结构用于光纤光栅的黏贴。利用COMSOL Multiphysics 5.2分别对比了悬臂梁和等强度梁在受力大小相同的情况下的应力应变,选择了加工方便、更贴合实际的悬臂梁结构。本设计中使用的是长为90 mm,宽为2 mm,厚度为0.2 mm的等截面悬臂梁结构。
图5和图6分别为等截面梁和等强度梁的仿真结果。

图5 等截面梁应力分析结果

图6 等强度梁应力分析结果
在仿真过程中,分别设计厚度相同、长度相同的悬臂梁结构,从图5和图6的仿真结果中可以看出,在底端加以相同大小的力后,等截面悬臂梁和等强度悬臂梁的受力情况不同。等强度悬臂梁从底端到顶端应变强度相同,而等截面悬臂梁的应变效果更加明显,于是测量系统最终选择等截面悬臂梁[15]。
利用仿真软件对全长90 mm的等截面悬臂梁进行应力大小分析,从仿真结果(图7)中可以看出,其中应力最大处为距离底端75 mm处,此处用于光纤光栅的粘贴。等截面梁端部添加一个管型的阻流元件,经过数值解析可得,为了使阻流元件获得最大的粘滞力,管型阻流元件的直径与外管道内径之比为0.6。
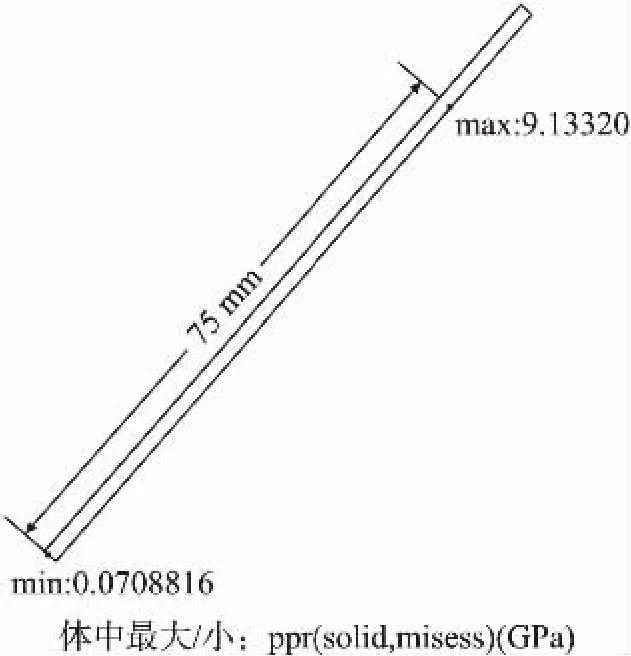
图7 应力最大最小位置受力图
3 实验研究
配置不同粘度的聚丙烯酰胺溶液,用标准粘度计测得在24.4℃条件下水、牛奶以及4种不同粘度的聚丙烯酰胺溶液的粘度值,如表1所示,将此组溶液作为标准液进行标定实验[16]。

表1 6种溶液的测量结果
3.1 线性度实验
选定流量为100 mL/min,在相同温度条件下,对6种溶液进行测量,当管道流过不同的6种溶液时,波长变化量与粘度的对应关系如表1所示。在实验过程中,选用中心波长为1 549.995 nm的光纤光栅,并利用动态光纤光栅解调仪解调出中心波长的变化量。
从图8可以看出η和Δλ呈线性关系,与理论推导的结果相一致,说明利用光纤光栅测量粘度的方法可行,继而用MATLAB工具进行最小二乘法拟合便可得出粘性力式(12)的系数m=0.669。

图8 粘度η与中心波长变化量Δλ的关系
3.2 误差分析
在本次误差探究实验中,首先温度处于一个稳定的室温水平,尽量保证光纤光栅测试时不受到温度带来的影响。利用BT101L流量型智能泵控制流量范围,分别测得在 50 mL/min、75 mL/min、100 mL/min、125 mL/min、150 mL/min的流量下6种溶液中心波长的变化量,实验结果如图9所示。
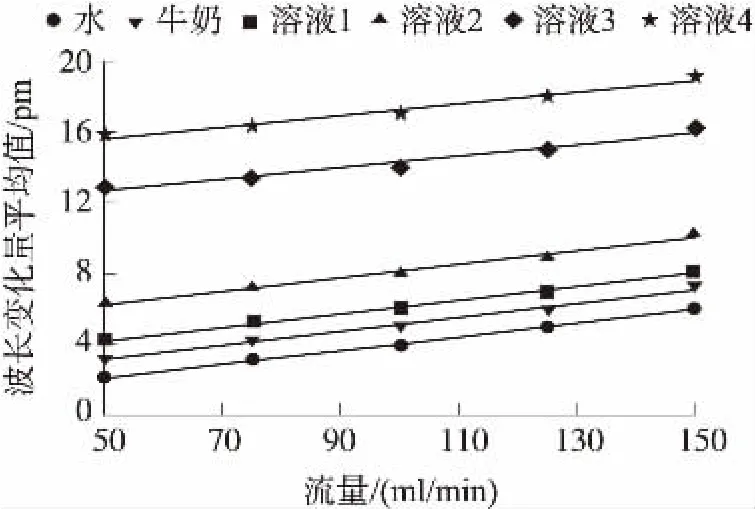
图9 流量与波长变化量的关系
经分析,随着流量的增大,同一种溶液的波长变化量逐渐增大;在同一流量条件下,随着溶液粘度的增大,波长变化量逐渐增大,符合预期结果。流量不同,拟合系数m的大小不同。
由于在相同的管道内,内径相同,内壁粗糙度相同,液体自身特性随粘度的增大发生改变,随着流量和液体粘度的增大,波长的变化量逐渐增大,但整体符合线性关系,与理论分析的结果相同。
3.3 比对试验
配置六组不同粘度的溶液,在同等温度、同等流量条件下,进行验证性实验,测得当不同溶液通过的波长变化量,代入公式计算得出6种溶液的粘度值,并和标准粘度计测得的粘度值进行对比,如表2所示。
经过结果对比分析,发现等截面梁式粘度计对于低粘度的溶液比较敏感,粘度大的溶液误差较大。中心波长变化量与粘度值呈一次线性关系,测量结果可靠。验证了此粘度测量方法的可行性。
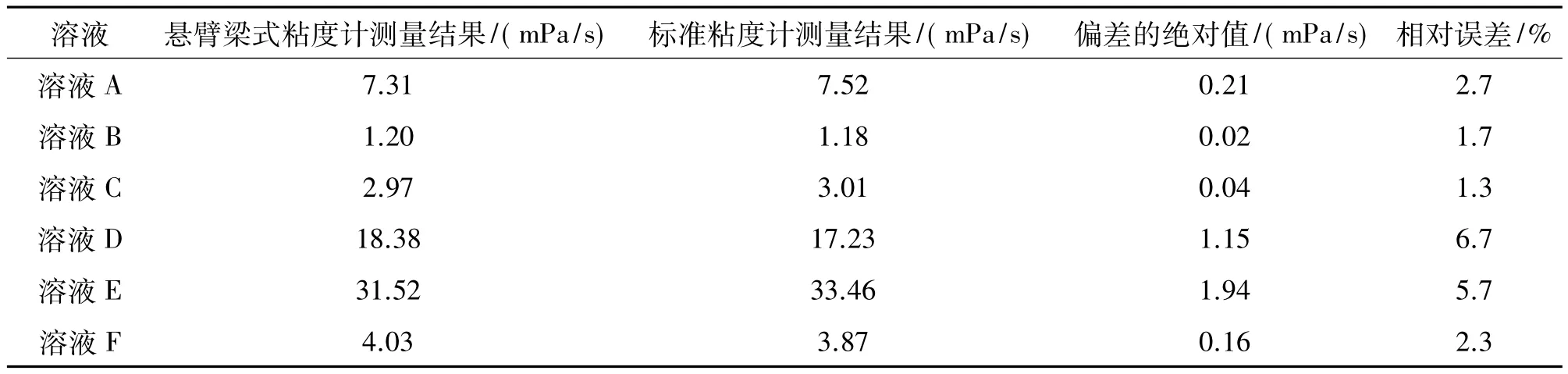
表2 6种溶液粘度结果对比
4 结论
经过三组实验结果的分析,验证了等截面梁结构结合光纤光栅测量粘度的可行性,对进行在线粘度测量的探究提供了一定的研究参考[17]。但是,由于悬臂梁弹性材料的限制,测量结果信号灵敏度不高,而且光纤光栅对于温度十分敏感,所有的测量结果都是在保证同一温度、压强条件下获得的。接下来的研究中,将会进一步提高灵敏度,进行温度补偿,构建完整的在线粘度测量系统。
[1] 吴德志,徐东亮,吴耀楚.粘度测定原理与应用[J].中国仪器仪表,2002(6):41-43.
[2] 张博驰.基于毛细管法的在线液体粘度测量系统的研究[D].广西大学,2014.
[3] 赵梦军,戴尔晗,徐君,等.数字旋转式粘度计软硬件设计[J].微型机与应用,2016(9):37-40.
[4] 李鹏,徐立军,姜印平.基于电磁感应的液体粘度在线测量方法研究[J].仪器仪表学报,2002,23(s2):870-872.
[5] 曹丽,董俊良,孙武峰.液体粘度在线测量的方法研究[C]//中国仪器仪表学会2010年学术产业大会,2010.
[6] 沈小燕.光纤光栅应变传感及扩大应变传感范围的技术研究[D].天津:天津大学,2010.
[7] 唐为义.流体粘度在线测量系统的设计与研究[D].青岛:青岛科技大学,2008.
[8] 张国忠,张足斌.管流液体的有效剪切速率[J].油气田地面工程,2000,19(1):1-3.
[9] 施庆珊,王计伟,欧阳友生,等.非牛顿流体粘度测定方法研究进展[J].发酵科技通讯,2011,40(2):42-45.
[10]吴今哲,朴相范,金哲.在线测定液体粘滞系数的一种机理及方法[J].物理测试,2005,23(2):49-51.
[11]Kazys R,Mazeika L,Sliteris R,et al.Measurement of Viscosity of Highly Viscous Non-Newtonian Fluids by Means of Ultrasonic Guided Waves[J].Ultrasonics,2014,54(4):1104-1112.
[12]郭伟,李新良,宋昊.表面粘贴光纤光栅传感器的应变传递分析[J].计测技术,2011,31(4):1-4.
[13]樊星.基于光纤光栅的扭矩传感系统的研究[D].天津:天津大学,2013.
[14]孙培元,赵美蓉,马金玉.两种典型扭振式粘度测头的灵敏度对比分析[J].传感技术学报,2013,26(1):53-57.
[15]刘聪,赵美蓉,马金玉.基于柔性铰链的液体粘度测量方法研究[J].传感技术学报,2015(3):310-314.
[16]白生宝,肖迎春,黄博,等.FBG传感器应变标定方法[J].振动、测试与诊断,2016,36(2):321-324.
[17]杨隆杰.在线液体粘度传感器研究[D].电子科技大学,2015.

陈 曦(1990-),女,硕士研究生,天津大学精密仪器与光电子工程学院,主要研究方向为液体粘度测量,chen0510xi @163.com;

赵美蓉(1967-),女,教授及博士生导师,天津大学精密仪器与光电子工程学院,主要从事光电测控技术 视觉检测技术和微纳测控技术的科研与教学,meirongzhao@tju.edu.cn;

黄银国(1978-),男,副教授及硕士生导师,天津大学精密仪器与光电子工程学院,主要从事光电传感检测技术,hyg @tju.edu.cn。
Study on Measurement Method of Liquid Viscosity Based on Fiber Bragg Grating*
CHEN Xi,ZHAO Meirong*,HUANG Yinguo
(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)
According to the online measurement of liquid viscosity,a new measuring method based on the fiber Bragg grating(FBG)is proposed.Through this method,the liquid viscosity can be derived from the variation of the FBG center wavelength.This method,the viscosity can be obtained by the fluid flowing,is a new exploration and breakthrough.Using FBG to sensing the stress change of cantilever beam caused by viscous force on the surface of the blocking element with the liquid flowing.Then,the stress change will be calculated by the center wavelength variation obtained from the FBG interrogator,thereby the corresponding viscosity value can be gotten.Through the experimental study,the measurement system was calibrated by the standard viscosity liquids,and the mathematical model between the center wavelength variation and the liquid viscosity was established.Eventually,the verification experiments,test results of a group of liquid viscosity from this measurement system comparing with the result from the standard viscometer,has verified the feasibility of the experimental method.
liquid viscosity online measurement;fiber bragg grating;wavelength variation;blocking element
TP23
A
1004-1699(2017)02-0189-05
C:7230
10.3969/j.issn.1004-1699.2017.02.004
项目来源:国家重大科学仪器设备开发专项项目(2013YQ030915);国家自然科学基金青年科学基金项目(61304246)
2016-07-25 修改日期:2016-10-13
