基于石英传感器的动态称重数据处理算法研究
2017-04-13王中立李丽宏
王中立,李丽宏
(太原理工大学信息工程学院,太原030024)
传感器信号处理
基于石英传感器的动态称重数据处理算法研究
王中立,李丽宏*
(太原理工大学信息工程学院,太原030024)
通过对以石英晶体传感器为称重单元的动态称重系统称重信号中干扰信号的分析,得出其称重信号中存在大量干扰信号,包括高频噪声和低频噪声,此外车辆行驶时自身振动、轴型、行驶速度以及加速度都会影响动态称重精度。针对以上问题,提出先利用小波变换算法对称重数据进行滤波预处理,然后再经过EEMD算法以及信号重构算法进一步处理。将以上信号处理算法通过仿真以及运用于现场,能够使称重数据误差控制在2%以内,达到了良好的称重效果。
动态称重;信号处理;小波变换算法;EEMD算法;信号重构算法
当前动态称重系统使用的称重传感器主要是弯板式传感器和电阻应变式传感器,经过长期使用这两种传感器,发现它们存在以下缺陷:电阻应变式传感器受外界冲击干扰影响比较大,称重精度低,寿命短[1];弯板式传感器在使用过程中稳定性和重复性差,寿命短,难以维护[2];当车辆高速通过基于这两种传感器的动态称重系统时,称重精度差。针对以上两种称重传感器的称重缺陷,提出了基于石英晶体称重传感器的动态称重系统。和其他两种称重传感器相比,石英晶体式称重传感器具有安装简便,称重范围大,维护简单,长期稳定,称重效率和称重精度高等优点[3]。
基于石英传感器的动态称重系统称量的动态称重信号可分为两部分,即车辆的静态载荷和车辆的动态载荷[4](即干扰信号)。动态载荷产生的原因是在采集信号过程中存在各种噪声的干扰,噪声主要由高频信号和低频信号组成。高频噪声主要由系统电气特性、发动机转动、加速状态载荷以及高速行驶时轮胎噪声等因素引起的;低频噪声主要由路面的平坦状况和车辆行驶中自身振动等因素引起的。静态载荷信号、低频噪声信号和高频噪声信号是主要实时采集的信号。因此,对采集到的称重信号进行正确处理,是动态称重系统信号处理的核心[5-7]。
在动态称重系统中为了处理这些混合信号,使用的主要信号处理算法有BP神经网络算法、RBF神经网络算法、小波变换算法和卡尔曼滤波算法等。但是,这些算法在动态称重信号处理中,都存在着一定的局限性。本文根据以上算法的不足,提出先利用小波变换算法对称重数据进行滤波预处理,再对预处理后的信号进行 EEMD(Ensemble Empirical Mode Decomposition,集合经验模态分解)算法分解,得出IMF(Intrinsic Mode Function,本征模态函数分量)分量,最后对本征模态函数分量通过信号重构算法进一步处理。
1 石英晶体传感器概述
石英晶体传感器是动态称重系统的称重单元,它能够在车辆通过过程中检测车辆轮胎的动态力,进而计算出轮重、轴重以及整车重。现如今,石英晶体传感器普遍作为动态称重系统的称重单元,这是由于它有如下优点:(1)长期使用,具有良好的稳定性;(2)测量范围广,从低速到高速,可实现0~200 km范围内的测量;(3)温度变化对其影响较小; (4)防护等级高,为IP68;(5)安装维护方便;(6)可适应各种道路,并在其表面有10 mm可研磨层,确保其与路面保持平整。
1.1 石英晶体传感器工作原理
石英晶体是石英晶体传感器的敏感元件,石英晶体传感器的工作原理框图如图1所示。并且此传感器的工作原理是基于石英晶体的压电效应[8],其把汽车轮胎的压力信号转换成电荷信号,然后再通过电荷放大电路及电荷电压转换电路转换成电压信号。

图1 石英晶体工作原理框图
1.2 石英晶体传感器称重信号分析
在基于石英晶体传感器的动态称重系统中,石英晶体传感器的单轴额定载荷为30 t,所以,石英晶体传感器稳定工作的轴重称量范围0~30 t。首先石英晶体传感器测量的是行驶车辆的轴重,然后,再把各个轴重信号汇总,得出车辆动态称重信号[9]。车辆轴重信号主要通过石英晶体传感器进行采集,此称重传感器在路面上的分布图如图2所示。传感器位于在路面上凿开的深50 mm,宽72 mm的凹槽内,并在上面铺上可被研磨的承载垫。

图2 石英晶体传感器路面摆放图
如图3所示,图中蓝色方块为石英晶体称重传感器,当轮胎接触传感器上的承载器时,会有信号输出,但由于其特有的结构特点,造成有效称重距离比较短,轮胎接触传感器时间短暂,采集数据较少,如图3所示。

图3 石英晶体传感器信号
图4所示为某三轴车经过基于石英传感器的动态称重系统时采集到的称重信号波形图,图中有3个波峰,每个波峰代表一个轴重信号。当轮胎接触称重传感器时,称重信号缓慢上升,到完全接触传感器时,称重信号达到最大值,然后称重信号缓慢下降,达到称重初始值。这是由于轮胎刚开始接触传感器时,轮胎同时接触地面和传感器,地面给轮胎提供一个支撑力,所以信号缓慢上升,当轮胎全部接触传感器时,此时输出轴重信号最大,但时间短暂,再加上前文分析的各种干扰因素的影响,造成称重信号波动范围比较大,因此,为了更好的去除噪声,在信号处理过程中加入降噪处理算法。
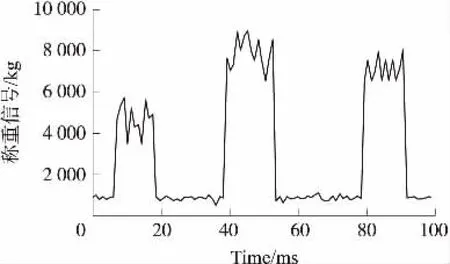
图4 称重波形图
2 称重信号滤波预处理
2.1 小波变换原理
从信号去噪学的角度来分析,可以把小波去噪过程看作一个信号滤波过程。由于滤波后,还能够保存其图像特征,所以它又区别并优于滤波器。实际上可以认为小波去噪是包含特征的提取以及滤波器这两个方面,并得出以下小波滤波原理框图如图5所示。

图5 小波滤波原理框图
小波变换在信号处理方面的最重要应用是进行信号滤波,而噪声信号经常是非理想的白噪声,包含有很多突变或者尖峰脉冲信号,而小波变换对此类信号具有很好地滤波作用[10-11]。在动态称重系统中,采集的称重信号中噪声频带分布明确,所以可以采用小波变换分析算法对动态称重信号进行降噪处理,来处理采集的称重信号中含有的突变或者尖峰信号,轴重信号小波分解过程如图6所示。
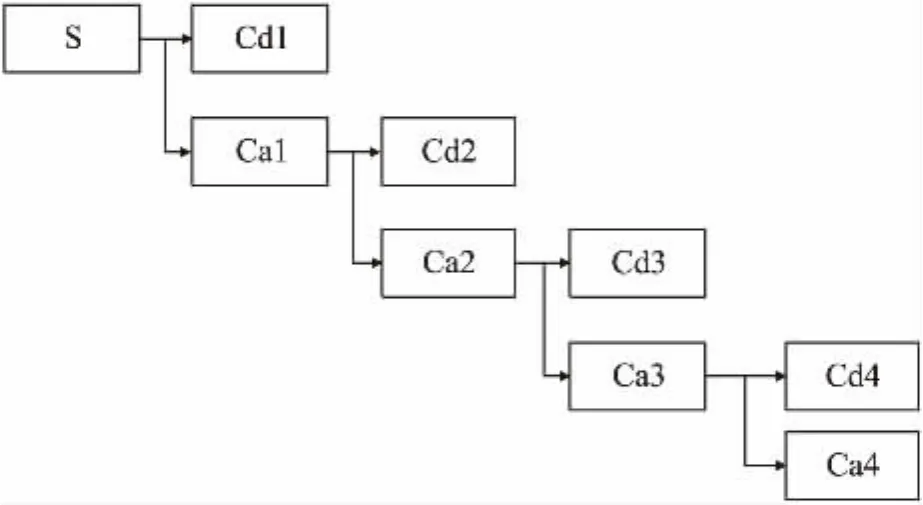
图6 轴重信号小波分解图
本文中把轴重信号分为四层,如图6所示,在第1、2、3、4层中高频部分分别是Cd1、Cd2、Cd3、Cd4,含有电气特性、发动机转动、加速状态载荷以及高速行驶时轮胎转动等因素引起的高频噪声,这些高频噪声应去除掉。在动态称重系统中,轴重信号处在低频部分中,小波分解后该部分信号主要在第4层低频部分Ca4中,在处理时进行保留。最后对小波分解处理后的信号进行信号重构,得到小波预处理后的轴重信号。
2.2 试验验证
利用图4所示的称重信号波形进行小波变换算法验证。本文采用MATLAB R2014a进行小波降噪分析,经过多次仿真结果对比,采用db4小波分解函数,小波分解称重数据4次,其主要程序命令:[c,l]= wavedec(Xdata,4,‘db4’);%Xdata为待分解数据,4为分解次数,db4为小波基分解函数 A4=wrcoef (‘d’,c,l,‘db4’,4);%根据小波分解结果,重建节点4系数。
对图4的原始称重信号波形进行小波滤波后,得到如图7所示图形。从图7看可以看出,经过小波变换算法预处理后,信号波动幅度变小,但仍然存在较多干扰噪声,需进一步处理。

图7 小波滤波后波形图
3 EEMD及信号重构算法原理
3.1EEMD基本原理
EEMD以EMD为基础,EEMD的基本理论是:首先,给目标信号施加一系列的高斯白噪声。然后把得到的混入白噪声的总信号进行EMD分解,得IMF分量及残余项[12]。IMF分量具有以下两个特点:①函数曲线穿过零极点的个数相等或至多差一个;②用三次样条曲线分别连接函数曲线的极大值点以及极小值点,形成上包络线和下包络线,并且它们之间距离的均值必须为零。
EEMD算法分解步骤如下:
①给目标信号 x(t)施加一系列高斯白噪声mi(t),得到总的信号Xi(t),即
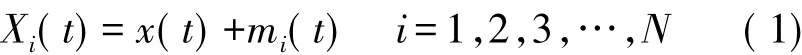
式中:mi(t)代表地i次添加的白噪声,Xi(t)代表第i次得到的总的信号。
②求出Xi(t)所有的极大值和极小值点,画出上包络线和下包络线,计算出上下包络线的均值hi(t),作Xi(t)与hi(t)的差值,即

式中:imfij是第 i次插入高斯白噪声而得到的第 j分量。
③重复步骤②直到imfij(t)满足本征模态函数的两个条件为止。其中,imfij(t)含有高次谐波,因此与Xi(t)作差,去除高次谐波,得到一个差值
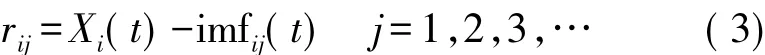
式中:rij表示第 i次施加白噪声后,得到的第 j残余量。
④把差值rij再作为输入信号,重复步骤①到步骤③直到n阶的函数rij不再能通过EMD分解成一个本征模态函数,而是一个单调函数为止[13]。此时

⑤可以把信号x(t)看作一系列imfij与残余项Res之和,即
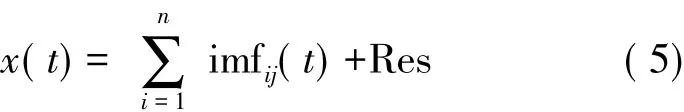
式中:Res是残余项,它是一个平滑的单调函数。imfij函数按频率由高频到低频顺序排列,频率成分在每一段是不同的,在同一IMF中各瞬时频率也是不同的。
3.2 EEMD分解后信号重构算法
车辆的轴重信号主要是低频信号,频率范围大概在5 Hz~18 Hz之间,所以可以通过反应称重信号的一部分本征模态函数来重构车辆的重量,称重信号经过EEMD分解后存在模式索引k1和k2使车辆实际称重信号y(t)由k1+k2-1个IMF分量来实现,如式(6)所示
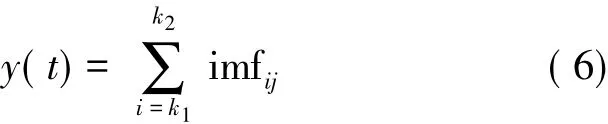
对每个IMF分量进行快速傅里叶变换,在频带上分别计算每个IMF的总能量[14]E(j),5 Hz~18 Hz之间称重信号频带的能量为Eh(j),j=1,2,…,n,且n为分解的IMF分量的个数。所以,k1和k2分别为

式中的实际意义是:当称重信号频带能量和对应的所有IMF分量分别在整个频带能量的比值比阈值δ大时,则保留此IMF分量,这是因为满足此条件的IMF分量含有车辆实际重量信号,可以用来进行信号重构;当两者比值比阈值δ小时,则舍弃此IMF分量,这是因为可以认为此IMF分量中不含车辆重量信号,只包含其他噪声信号,不用于信号重构。此式中δ的取值尤其重要,过大过小都会影响信号重构,过大则会存在包含有较多噪声的IMF分量,过小则会舍弃含有车辆实际重量信号的IMF分量,都不利于信号重构,通过仿真发现,当IMF分量的频带能量占整个频带能量一半以上,即δ取值为0.5时,保留此IMF分量并用于信号重构,并且保留的分量之间相互独立,从而能达到最优信号重构[15]。
3.3 试验分析
从预处理后的称重信号中选取一段来进行分析,得到如图8所示的采样信号波形图。

图8 采样信号值

图9 EEMD分解后各IMF分量的波形图
对此信号加入高斯白噪声,得到混合信号。经过EEMD处理后的波形图如图9所示,从图9可以得知,经过EMD的层层分解,能把三轴车的轴重电压信号按频率从高到低从噪声中分离出来。因为EMD分解基底函数具有自适应的特点[16],所以得到的IMF1到IMF5是信号的真实反映。最后,在这5个分量的基础上进行重信号构,即可得到去掉噪声的真实轴重信号。
为了进行信号重构,首先对EEMD分解采样信号而得出的5个IMF分量以及采样信号进行快速傅里叶变换,分别在频带上求出5个IMF分量的总能量和采样信号的总量,根据式(7)求出能量百分比并绘制出如图10所示的能量百分比图,从图10可以看出IMF分量中的IMF3和IMF4的频带域能量分别占采样信号频带域能量的一半以上,所以选择IMF2,IMF3来进行信号重构。

图10 各IMF分量的能量百分比分布图
4 实验仿真及结果分析
本文研究的算法曾在现场进行试验并采集过车的轴重数据,对采集到的数据随机抽取10组,先利用小波变换算法进行滤波预处理,然后经过EEMD算法和信号重构算法再处理后,把处理过的轴重数据进行累加,得出车辆静态载荷,验证结果如表1所示,其中,两轴(12型)空车整车静态载荷为7 250 kg,四轴(115型)重车的整车静态载荷为39 780 kg。数据处理结果如表1。

表1 现场测试数据
从表1可以得出经过小波变换算法预处理后称重误差保持在3%~7%之间,不能达到良好的滤波效果,最后对预处理后的称重数据通过EEMD以及信号重构算法进一步处理后,能使称重数据误差控制在2%以内。本文研究的算法主要是处理轴重数据,把处理后的数据累加后得出车的静态载荷,所以,此方法可以适用于的测量范围即石英晶体传感器的轴重称量范围0~30 t,能完全满足不同车型的动态称重称量精度的要求。
5 结束语
本文针对以石英晶体传感器为称重单元的动态称重系统称重信号特点,首先利用小波变换算法进行滤波预处理,能够去除高频以及部分低频干扰噪声信号,然后利用EEMD算法对预处理后的称重信号进行再次滤波处理,能有效解决信号分解时出现的模态混叠现象和消除低频干扰信号,并通过信号重构算法对本征模态函数分量进行重构,得出行驶车辆的动态称重。最后,验证结果表明称重数据的最大误差低于2%,满足动态称重系统精度要求,具有实用价值。
[1] 朱子健,刘旭初.电阻应变式称重传感器的滞后补偿[J].衡器,2000,29(6):21-25.
[2] 傅宇浩.弯板式称重传感器技术研究[J].中国交通信息产业,2006(9):121-123.
[3] 李晓宝,简水珍,彭恢湘.压电石英称重传感器在公路动态称重中的应用[J].公路与汽运,2012(2):92-94.
[4] 刘九卿.压电石英称重传感器及其在动态公路车辆称重系统中的应用[C]//中国衡器协会称重技术研讨会,2007.
[5] 刘玉龙.基于HHT技术在动态称重信号滤波中的应用[D].太原:太原理工大学,2015.
[6] 沈小倩,蔡晋辉,姚燕.遗传神经网络在动态称重中的应用[J].传感技术学报,2010,23(9):1359-1363.
[7] 黄必飞,冯志敏,张刚.压电薄膜车辆动态称重系统算法研究[J].传感技术学报,2016,29(6):941-946.
[8] 吕宏强.石英晶体传感器[J].宝鸡文理学院学报:自然科学版,2003,23(1):52-54.
[9] 周正飞,鲁雄文,谭永营.基于压电石英传感器的动态称重系统的设计[J].汽车实用技术,2015(4):66-68.
[10]毛东杰,张晓濛,蒋小文.基于小波变换的表面肌电信号低功耗压缩滤波算法[J].传感技术学报,2016,29(5):647-653.
[11]王继成.小波分析在信号去噪声中的应用[D].天津:南开大学,2006.
[12]郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J].振动与冲击,2013,32(21):21-26.
[13]王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学,2010.
[14]张永德.基于经验模态分解的小波阈值信号去噪研究[D].昆明:昆明理工大学,2011.
[15]冯久超,潘水洋.基于经验模态分解的生命信号提取算法[J].华南理工大学学报:自然科学版,2010,38(10):1-6.
[16]师培峰,邱伟,樊孝春.基于HHT的自适应滤波方法在信号处理中的应用[J].强度与环境,2015(4):52-58.

王中立(1989-),男,硕士,主要研究方向为检测技术与智能仪表,wangli19890 @sina.com;

李丽宏(1963-),男,副教授,博士,主要研究领域为检测技术与智能仪表,ya721@163.com。
Research on Dynamic Weighing Data Processing Algorithm Based on Quartz Sensor
WANG Zhongli,LI Lihong*
(Information Engineering College,Taiyuan University of Technology,Taiyuan 030024,China)
Through the analysis of interference signal in quartz crystal sensor weighing system for weighing unit weighing signal,interference signal that a large number of the weighing signal,including high frequency noise and low frequency noise,in addition when the vehicle vibration,its axis type,speed and acceleration will affect the dynamic weighing accuracy.In view of the above problems,the paper puts forward that the wavelet transform algorithm is used to preprocess the weighing data,and then the EEMD algorithm and the signal reconstruction algorithm are used to deal with the problem.The above signal processing algorithm is simulated and applied to the field,so that the error control of the weighing data is less than 2%,and the result is good.
dynamic weighing;signalprocessing;wavelettransform algorithm;EEMD algorithm;signal reconstruction algorithm
TP183
A
1004-1699(2017)02-0236-06
C:7220
10.3969/j.issn.1004-1699.2017.02.012
2016-08-04 修改日期:2016-09-21
